概要
- ロジスティック回帰を例に、各種勾配降下法をコードレベルで理解
- 最急降下法、確率的勾配降下法、ミニバッチ確率的勾配降下法
- 各種勾配降下法を実装
- 行列計算はnumpyを使用
- 各種勾配降下法の挙動を可視化
1 最適化するロジスティック回帰の目的関数の導入
今回は、2クラス分類のロジスティック回帰を使用する。
(以下、2クラス分類のロジスティック回帰を、単にロジスティック回帰と呼ぶ。)
ロジスティック回帰の出力値は以下の式で表され、0から1の確率として得られる。
y^* = sigmoid(xw + b)\\
y^* : 予測値\\
x : 説明変数\\
w : 重み\\
b : バイアス\\
sigmoid(X) : Xを(0,1)区間に写像\\
例えば、2クラスA・Bを想定し、ロジスティック回帰の出力をクラスAである確率とすると、以下のようになる。
y^* : クラスAである確率\\
1-y^* : クラスBである確率(=クラスAではない確率)
そして、ロジスティック回帰では、予測値y*と正解ラベルyの差から計算される損失関数Lを最小化する回帰直線を求めることになる。この回帰直線を求める方法として勾配降下法がある。勾配降下法とは、損失関数から得られる勾配を使って、損失関数をより小さくする重みwとバイアスbを、逐次更新していく手法である。
詳細は省くが、プログラムで使用する勾配の計算部分とパラメータ更新部分は以下の通りである。
(1)勾配の計算\\
\frac{∂L}{∂w} = - \sum_{n=1}^{N}x_{n}(y - y^*)\\
\frac{∂L}{∂b} = - \sum_{n=1}^{N}(y - y^*)\\
(2)パラメータ更新\\
w ← w - \eta\frac{∂L}{∂w}\\
b ← b - \eta\frac{∂L}{∂b}\\
ただし、ηは学習率と呼ばれ、一回の更新でどれくらいパラメータ(w, b)を変化させるかという度合いと表す。
2 各種勾配降下法について
今回は、以下の3種類の勾配降下法を試す。
- 最急降下法
- 確率的勾配降下法(SGD)
- ミニバッチ確率的勾配降下法(MSGD(単にSGDと呼ばれることもある))
これらは、勾配を計算するときに使用するデータ数で区別することができる。
そして、確率的勾配降下法とミニバッチ確率的勾配降下法では、データをシャッフルする。こうすることで、上から順に1行ずつ処理するということが、ランダムにデータを抽出するということになる。
| 最急降下法 | 確率的勾配降下法 | ミニバッチ確率的勾配降下法 | |
|---|---|---|---|
| 使用するデータ数 / 勾配計算 | 全部 | 1つ | 数個(ミニバッチ) |
| データの選択順 | --- | ランダム | ランダム |
3 実装
まず、サンプルデータを準備する。
点(0, 0), (6, 6)の周りに、ランダムに50個ずつサンプル点を用意する。そして、片方(赤)の正解ラベルを「0」に、もう片方(青)を「1」にする。
import numpy as np
import matplotlib.pyplot as plt
d = 2
N = 100
x1 = np.random.randn(N//2, d)
x2 = np.random.randn(N//2, d) + np.array([6, 6])
x = np.vstack((x1, x2))
label1 = np.zeros(N//2)
label2 = np.ones(N//2)
label = np.hstack((label1, label2))
dataset = np.column_stack((x,label))
np.random.shuffle(dataset) #データ点の順番をシャッフル
x = dataset[:, :2]
label = dataset[:, 2]
plt.scatter(x1[:, 0], x1[:, 1], c='r')
plt.scatter(x2[:, 0], x2[:, 1], c='b')
plt.show()
plt.close()
次に、使用する関数を3つ定義する。
- シグモイド関数
def sigmoid(a):
return 1.0 / (1.0 + np.exp(-a))
- 現在のパラメータにおける、ロジスティック回帰の予測値を返す関数
def logistic(x):
return sigmoid(np.dot(x, w) + b)
- 勾配を返す関数
def grad(x, label):
error = label - logistic(x) # (正解ラベルy) - (予測値y*)
w_grad = -np.mean(x.T * error, axis=1) # 式(1) 上に記載
b_grad = -np.mean(error) # 式(1)
return w_grad, b_grad
そして、パラメータを適当に初期化した後、各種勾配降下法によるパラメータの最適化を行う。ここで、今回は手法ごとにプログラムを書き分ける手間を省くため、「minibatch_size」の大きさで、手法を区別する。
- 最急降下法(全部) : minibatch_size = N
- 確率的勾配降下法(1つ) : minibatch_size = 1
- ミニバッチ確率的勾配降下法(数個) : minibatch_size = 10
w = np.random.rand(d)
b = np.random.random()
eta = 0.1
# 1つ選択
# minibatch_size = N # 最急降下法
# minibatch_size = 1 # 確率的勾配降下法
minibatch_size = 10 # ミニバッチ確率的勾配降下法
# パラメータ更新毎の損失
loss_list = list()
for epoch in range(50):
for iteration, index in enumerate(range(0, x.shape[0], minibatch_size)):
_x = x[index:index + minibatch_size]
_label = label[index:index + minibatch_size]
w_grad, b_grad = grad(_x, _label)
w -= eta * w_grad
b -= eta * b_grad
loss_list.append(np.mean(np.abs(label - logistic(x))))
# 損失の確認
print(np.mean(np.abs(label - logistic(x))))
plt.plot(loss_list)
plt.show()
plt.close()
# 回帰直線の確認
bx = np.arange(-6, 10, 0.1)
by = -b/w[1] - w[0]/w[1]*bx
plt.xlim([-5, 10])
plt.ylim([-5, 9])
plt.plot(bx, by)
plt.scatter(x1[:, 0], x1[:, 1], c='r')
plt.scatter(x2[:, 0], x2[:, 1], c='b')
plt.show()
plt.close()
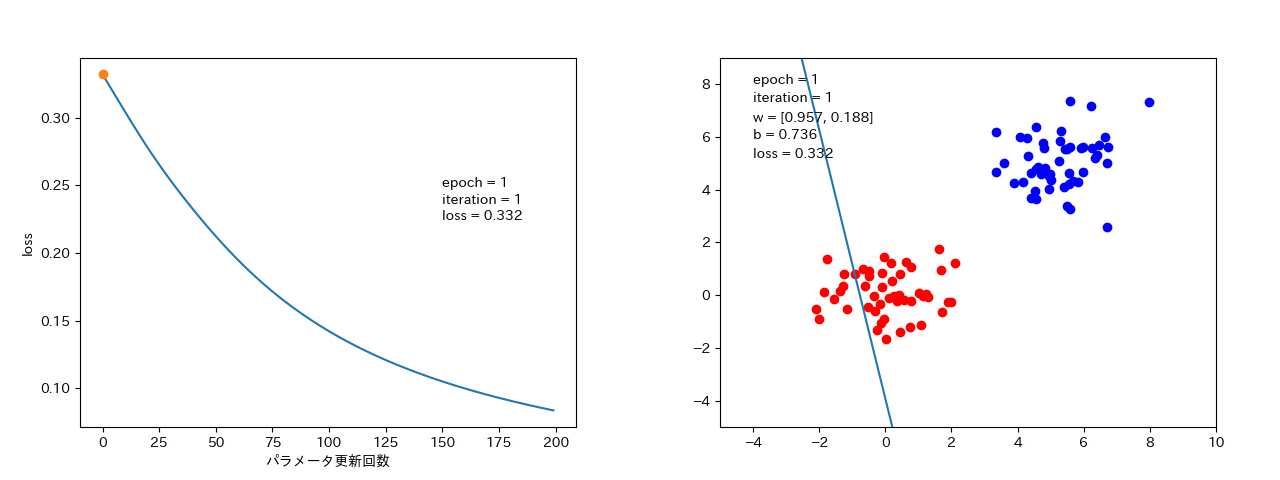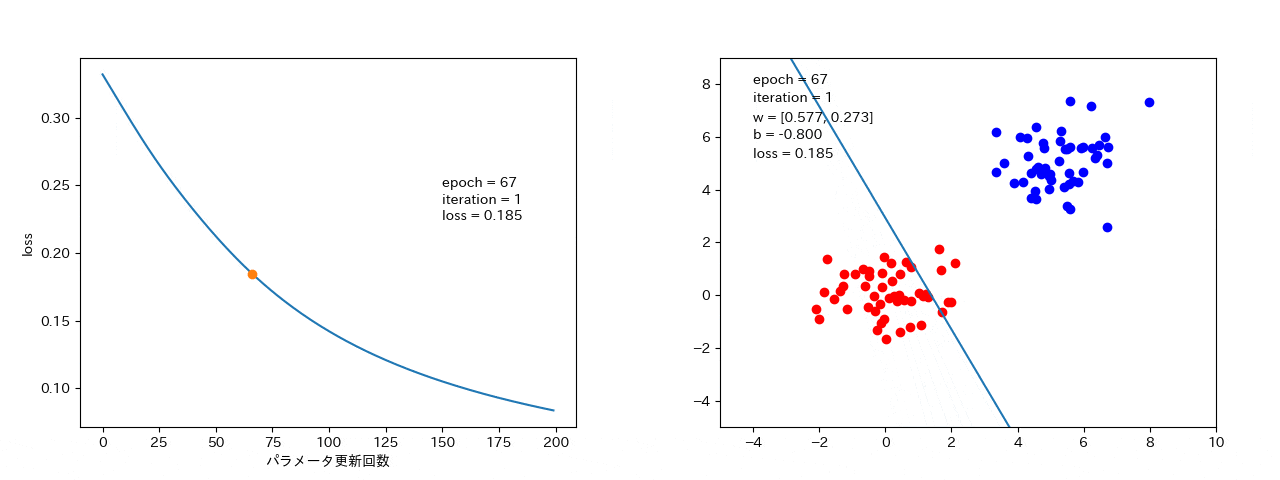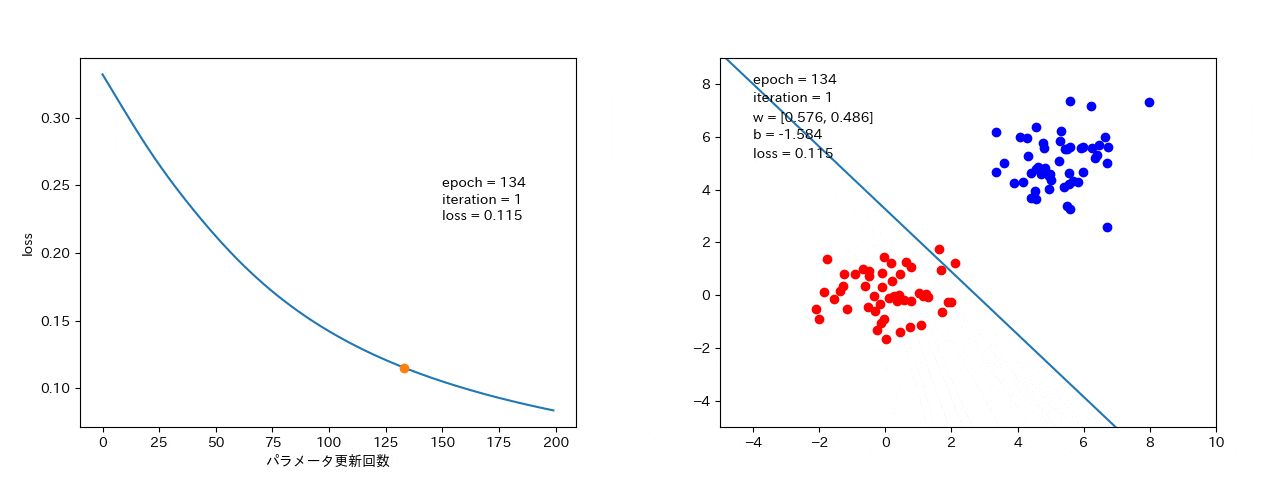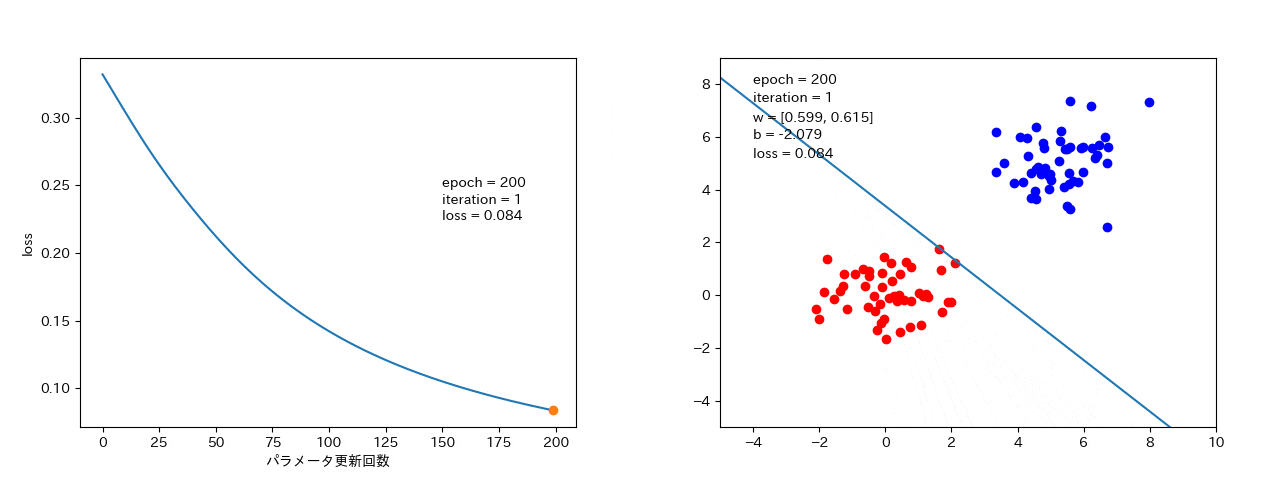
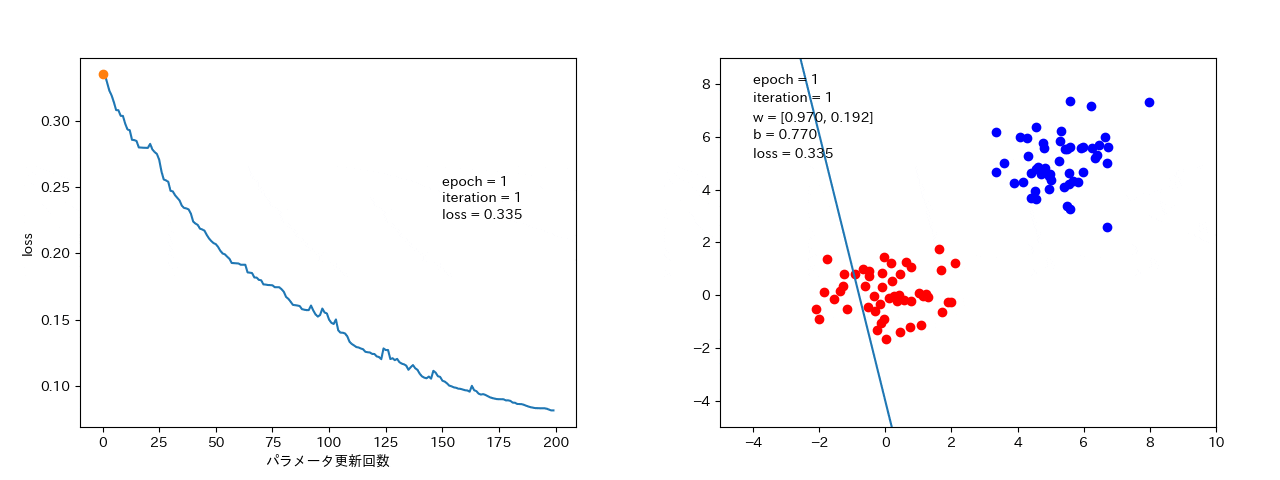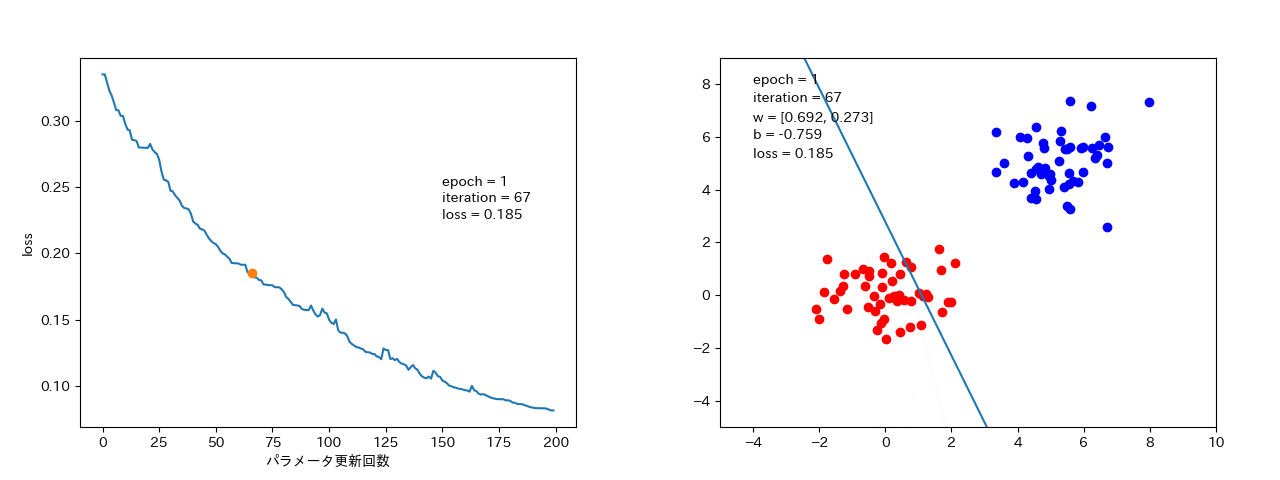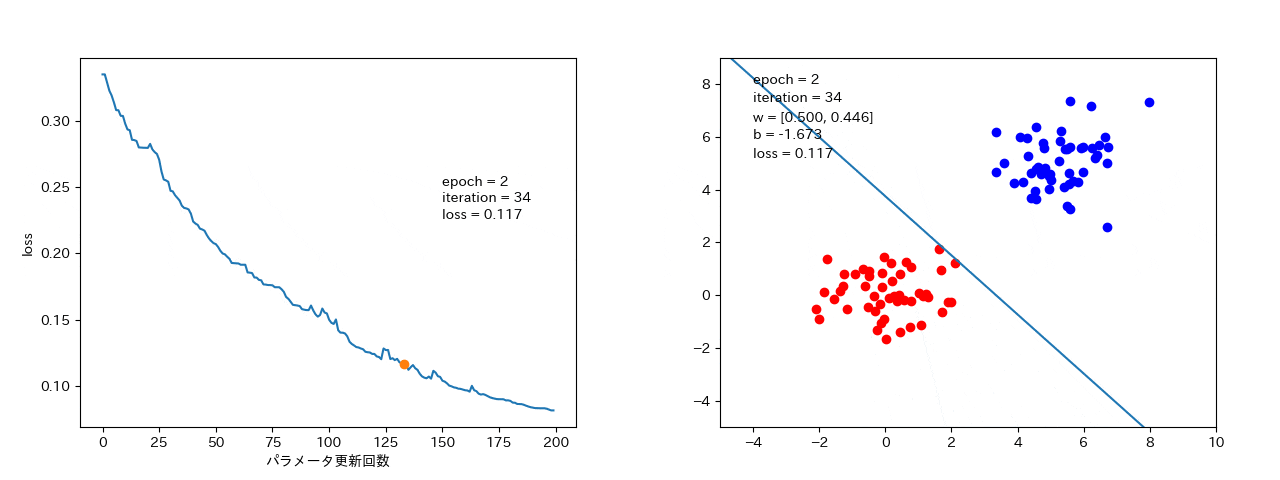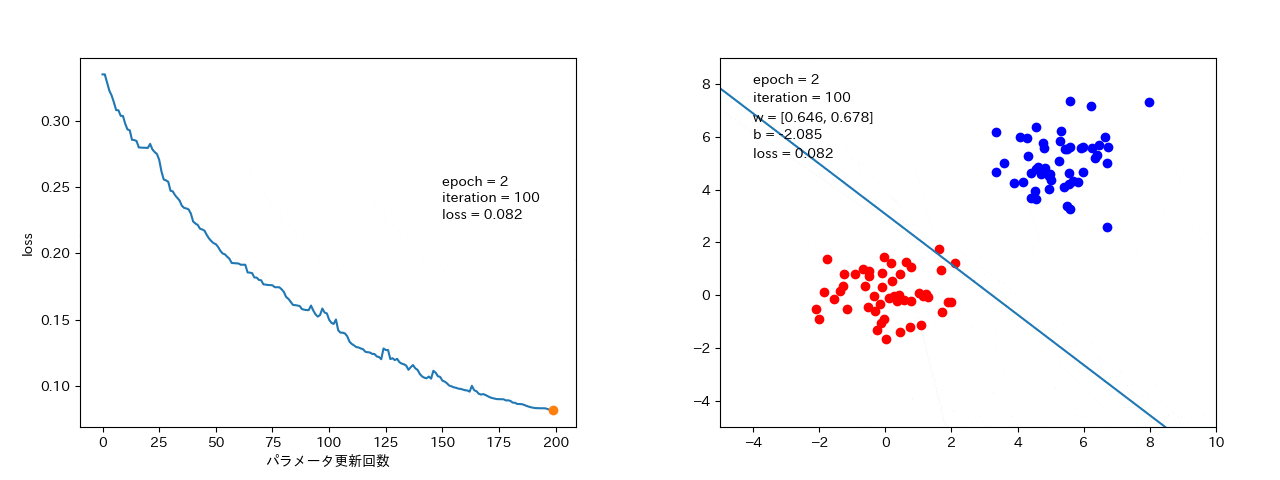
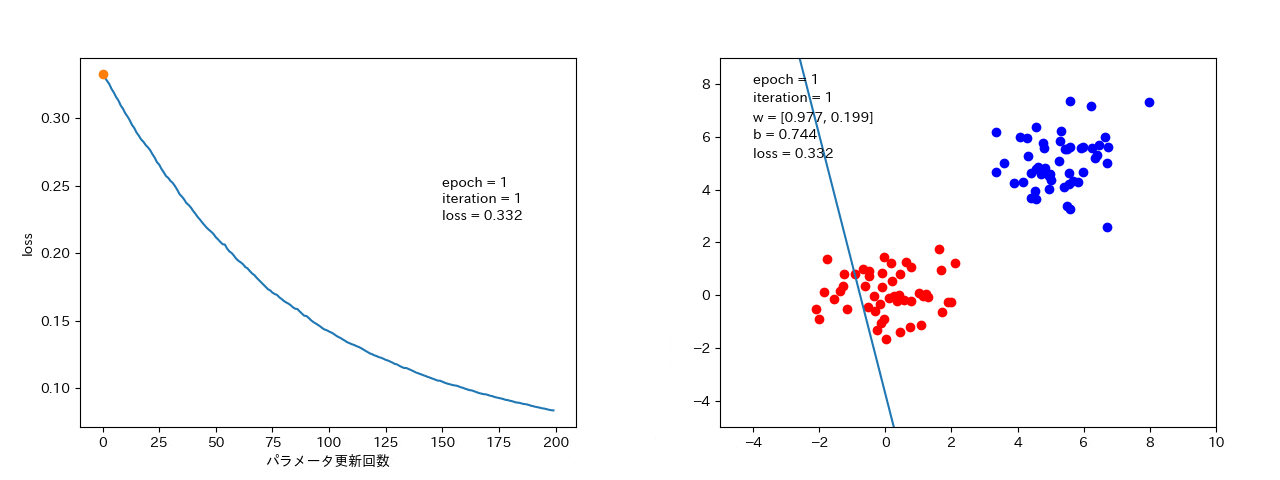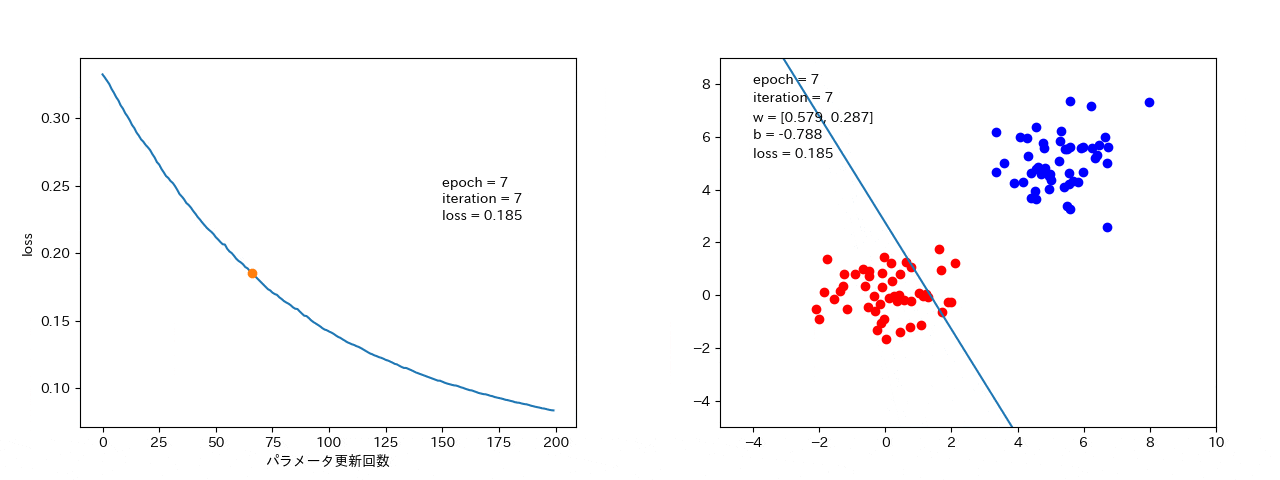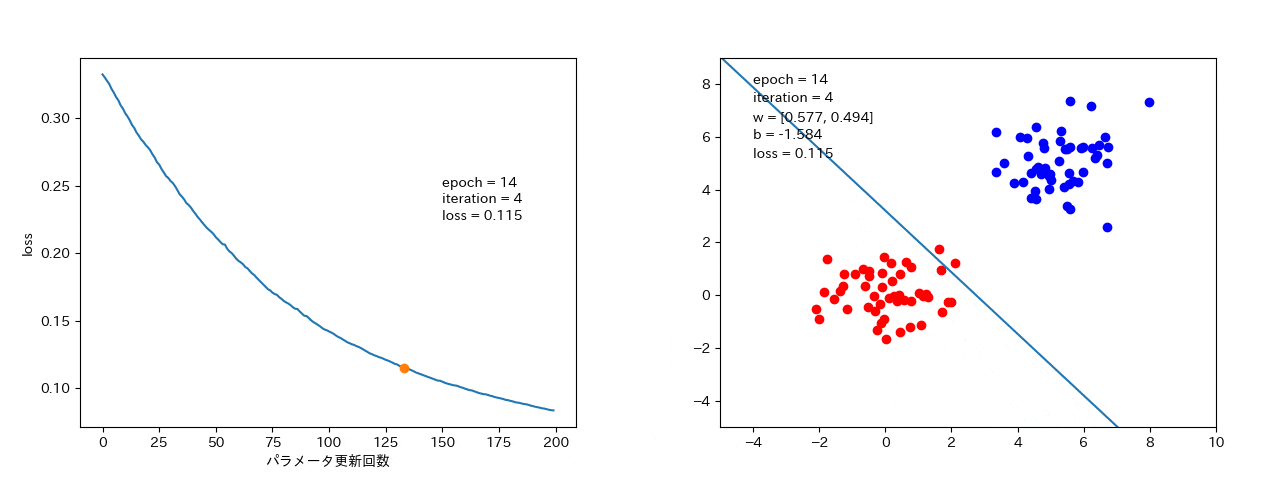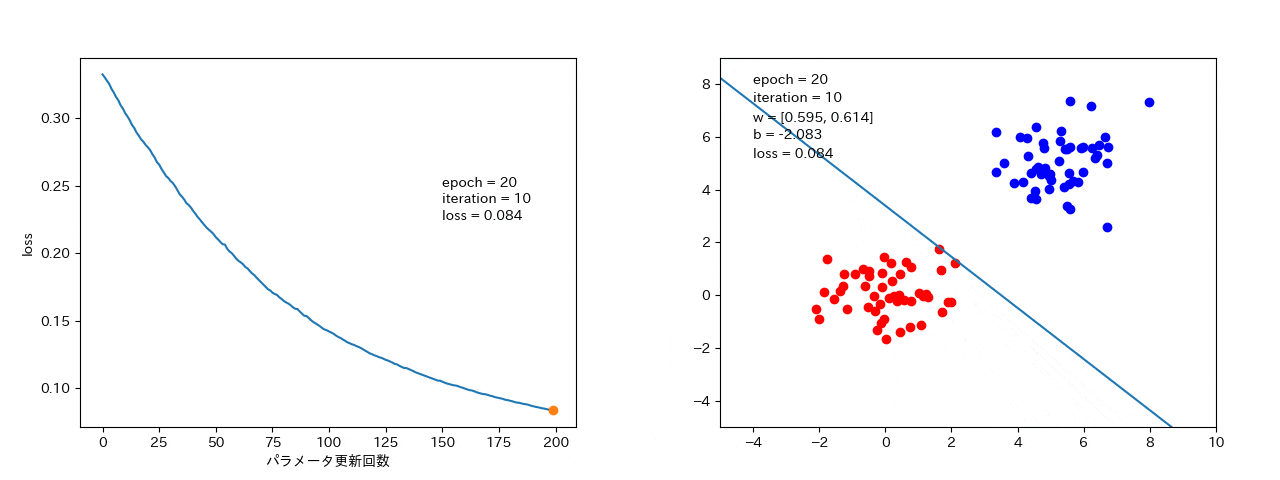
4 結果
最急降下法
全データから勾配を計算するので、損失が大きくなることはない。(最短で、最適解 or 局所最適解に落ちる。)
確率的勾配降下法
データ1つずつから勾配を計算するので、場合(ノイズの大きいデータ)によっては、損失が大きくなることもある。(解までは最短ではないが、局所最適解に落ちたとしても、抜け出して最適解に落ちる可能性がある。)
ミニバッチ確率的勾配降下法
minibatch_size = 10 のとき。
データ数個ずつから勾配を計算するので、確率的勾配降下法よりは、損失がなまされて、ばらつきは小さい。
最後に
実装と可視化が目的だったので、結果以上の考察はしてません。各種勾配降下法のメリット・デメリットは以下をどうぞ。