はじめに

　今回は、OpenCV3とPython3を使ってニューラルネットワークの学習をしてみます。
　画像処理とニューラルネットワークを組み合わせて使うケースがOpenCVだけで完結するので、ちょっとした検証に便利です。またOpenCVのPythonバインディングは、実体はC++で、PythonはC++のメソッドを呼び出すラッパーにすぎないので、学習はそこそこ高速に動作します。

■ 実行環境
・Python: 3.5.2
・OpenCV: 3.1

■ インストールと簡単な使い方はこちら
OpenCV 3（core + contrib）をPython 3の環境にインストール＆OpenCV 2とOpenCV 3の違い＆簡単な動作チェック

プログラム

最低限のプログラムです。
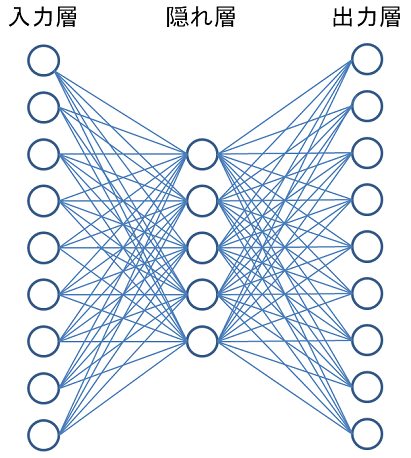
入力層：９
隠れ層：５
出力層：９

活性化関数：シグモイド
学習方法：バックプロパゲーション
学習データ：
　・入力データ
　　　[[1.2, 1.3, 1.9, 2.2, 2.3, 2.9, 3.0, 3.2, 3.3]]
　・出力データ
　　　[[0, 0, 0, 0, 0, 1, 0, 0, 0]]
検証データ：
　・入力データ
　　　[[1.4, 1.5, 1.2, 2.0, 2.5, 2.8, 3.0, 3.1, 3.8]]

ann.py

# -*- coding: utf-8 -*-
import cv2
import numpy as np

# ニューラルネットワークを生成
ann = cv2.ml.ANN_MLP_create()
# 入力層、隠れ層、出力層の設定
ann.setLayerSizes(np.array([9, 5, 9], dtype = np.uint8))
# 学習方法の設定
ann.setTrainMethod(cv2.ml.ANN_MLP_BACKPROP)
# 学習
ann.train(np.array([[1.2, 1.3, 1.9, 2.2, 2.3, 2.9, 3.0, 3.2, 3.3]], dtype=np.float32),
          cv2.ml.ROW_SAMPLE,
          np.array([[0, 0, 0, 0, 0, 1, 0, 0, 0]], dtype=np.float32))
# 検証
result = ann.predict(np.array([[1.4, 1.5, 1.2, 2.0, 2.5, 2.8, 3.0, 3.1, 3.8]], dtype = np.float32))
print(result)

実行結果

実行結果は以下のようになります。

(5.0, array([[-0.06419383, -0.13360272, -0.1681568 , -0.18708915,  0.0970564 ,  0.89237726,  0.05093023,  0.17537238,  0.13388439]], dtype=float32))

入力[[1.4, 1.5, 1.2, 2.0, 2.5, 2.8, 3.0, 3.1, 3.8]]に対する出力が[[-0.06419383, -0.13360272, -0.1681568 , -0.18708915, 0.0970564 , 0.89237726, 0.05093023, 0.17537238, 0.13388439]]になっていました。
学習させようとした出力が[[0, 0, 0, 0, 0, 1, 0, 0, 0]]ですので、学習時の入力に対して検証時の入力が多少ゆらぎがある状況で、検証結果は-0.1～+0.1の範囲に収まり、ほぼ意図した出力になっています。

※ 実行結果の１つめの値「5.0」は意味のない値だということです。

活性化関数

活性化関数のデフォルトはシグモイド関数です。

setActivationFunction(type, param1, param2)

で指定します。

指定例：

activate_function.py

ann.setActivationFunction(cv2.ml.ANN_MLP_SIGMOID_SYM, 0, 0)

引数	意味	デフォルト
type	活性化関数	シグモイド関数
param1	α	0
param2	β	0

方式	値	定数	数式
恒等関数	0	cv2.ml.ANN_MLP_IDENTITY	$f(x)=x$
シグモイド関数	1	cv2.ml.ANN_MLP_SIGMOID_SYM	$f(x)=\beta*(1-e^{-\alpha x})/(1+e^{-\alpha x})$
ガウス関数	2	cv2.ml.ANN_MLP_GAUSSIAN	$f(x)=\beta e^{-\alpha x*x}$

※ OpenCV 3.1.0 でフルサポートされている活性化関数はシグモイド関数のみとのこと。

終了条件

終了条件のデフォルト設定は、最大繰り返し回数：1000、最小変化量：0.01 の両方が設定されています。

setTermCriteria(val)

で指定します。

指定例：

criteria.py

criteria = (cv2.TERM_CRITERIA_MAX_ITER + cv2.TERM_CRITERIA_EPS, 1000, 0.01)
ann.setTermCriteria(criteria)

criteriaは、(type, maxCount, epsilon) の順に値をセットします。

・type

定数	意味	値
cv2.TERM_CRITERIA_COUNT	最大繰り返し回数	1
cv2.TERM_CRITERIA_MAX_ITER	最大繰り返し回数	1
cv2.TERM_CRITERIA_EPS	最小変化量	2

※ cv2.TERM_CRITERIA_COUNT と cv2.TERM_CRITERIA_MAX_ITER は別名の関係にあります。

バックプロパゲーションの設定

モーメント係数
２つ前のイテレーションと１つ前のイテレーションの差分量に対するモーメント係数を設定することができます。この値をある程度とっておくと、局所解にはまり込むのを予防してくれたり、収束を早めたりさせることができたりします。ただし、大きく設定してしまうと、最後のところで逆になかなか収束しなかったり、場合によっては発散してしまったりします。
　　経験則で、0.1 程度がよいとされています。デフォルト値は0.1に設定されています。

指定例：
momentum_scale.py
```
ann.setBackpropMomentumScale(0.1)
```
学習係数
学習速度を調整する微分係数です。小さすぎるとなかなか収束しなく、大きすぎると発散したりすることがあります。
経験則では、0.1 程度がよいとされています。デフォルト値は0.1に設定されています。

指定例：
weight_scale.py
```
ann.setBackpropWeightScale(0.1)
```
Resilientバックプロパゲーション
　OpenCV3は、上記２つのパラメータを指定するバックプロパゲーションだけでなく、Resilientバックプロパゲーションもサポートしています。
Resilientバックプロパゲーションは、学習の勾配が前回と今回で符号が変わったかどうかで学習係数を変更するアルゴリズムです。
- 前回と今回で符号が同じ場合：学習の勾配に重みをかけて学習を加速させる
- 前回と今回で符号が異なる場合：学習の勾配を減らして最適解に近づく
指定方法の詳細はこちら（リンク）

３層ニューラルネットワークと画像処理の関係について

　「OpenCV 3で犬と猫を分類できるように学習してみる」でBag Of Visual Words（BOW）を紹介しましたが、BOWでニューラルネットワークの入力を作成する方法がよく知られています。
　このあたりは、また後日紹介したいと思います。

OpenCV 3とPython 3でニューラルネットワーク