More than 3 years have passed since last update.

剛体球衝突アルゴリズムが少し分かるようになる記事

Last updated at 2020-08-06Posted at 2020-07-11

【2020/8/6追記】「LS-DYNAのCPMの解明のため」とありますが、調べたところ、LS-DYNAではこの記事で紹介した前提(完全弾性衝突)が成立していませんでした。2物体のInternal energyは保存されるものの、運動量及びTranslate kinetic energy(運動エネルギー)は保存されていません。
つまり何が言いたいかというと、本記事はLS-DYNAのCPM法の説明にはなりません。純粋に剛体球衝突アルゴリズムとしてお読みいただければと思います。

LS-DYNAのCorpuscular Particle Method (CPM)を使用しているのですが、複数種ガスの混合時の粒子数の比の影響(TotalのInternal energyに対するTranslate energyの比が粒子数比で異なる→Part/Particle PressureやCMPsensorの値が粒子数比で変化する。(Airbag Pressureは粒子数比によらず一定))を考察をしたいと思い、かなり目標から手前の内容ですが、剛体球衝突について勉強しました。
何番煎じかわかりませんが(Qiitaでも@yotapoonさん、@NatsukiLabさんがそれぞれ記事を書かれています)、自分なりに理解したことをまとめたいと思い書いています。

1. 剛体球/円盤衝突アルゴリズムとは

下図のようなシミュレーションを行う手法です。(図はWikipediaのKinetic theory of gasesより引用) 調べてみるとゲームプログラミング等でも使用されているようです。
気体分子運動論の解析でも使用されており、wikipediaのBaltzmann distributionの記事では粒子の衝突の結果、粒子の速度分布がMaxwell-Boltzmann分布に収束してゆくことが確認できます。
自分のモチベーションとしては、気体分子の速度分布を算出し、ガスの混合時に各ガスの運動エネルギーがどう変化してゆくか理解したいということがあります。

#2. 前提と数学的理解
まず、下記の2つが前提となります。特に大きさを持つというのがランダムな運動を実現するキモとなります。

球/円盤は直径・速度・質量を持つ
球/円盤は等速度直線運動をする=衝突以外で速度は変化しない

また、本記事はthermosimというgithubにアップされていたソースを対象に解説します。
このソースは、いわゆるTime-Step型のシミュレーションを採用しています。(こちらが詳しいです。https://qiita.com/NatsukiLab/items/476e00fea40b86ece31f)
なお、参考文献で示した記事でも同様/類似の手法が記載されていたため、一般的な手法と言えそうです。

###2.1.衝突判定
粒子i. jの時間$t$での座標を$r(t)$, 速度を$v(t)$,質量を$m$、直径を$d$とします。
まず、下記の式で、現時点で既に衝突している粒子の一覧を取得します。

|r_i(t) - r_j(t)|\leq\frac{1}{2}(d_i+d_j)

既に衝突しているというのがキモで、現在のステップ(時間$t$)で接触した粒子を接触前まで"巻き戻し"、巻き戻された時点での速度と座標から、速度ベクトルを更新します。（前ステップでは接触していないことは保証されています）

衝突している粒子がわかったら、次はいつ衝突したのかを計算します。
まず、相対速度、相対位置ベクトルを下記のように定義します。なお、時間$t=0$を前回のステップの時間とします。

v_{ij}=v_i-v_j\\
r_{ij}=r_i(0)-r_j(0)\\

粒子は等速直線運動をするので、前ステップから衝突までの時間を$t_c$として、衝突時の座標は下記のように示されます。

r_i(t_c)=r_i(0)+v_i(t)・t_c\\
r_j(t_c)=r_j(0)+v_j(t)・t_c\\

以上から、$|r_i(t) - r_j(t)|=\frac{1}{2}(d_i+d_j)$となるときの時間$t_c$は下記のように示されます。(実際、前ステップの時間を0としているので、$tc$は前ステップから衝突までの時間差分と同じ意味です。)

t_c=\frac{-r_{ij}・v_{ij}-\sqrt{(r_{ij}・v_{ij})^2-v_{ij}^2(r_{ij}^2-0.25(d_i+d_j)^2)}}{v_{ij}^2}

単純に上記は$|r_i(t) - r_j(t)|=\frac{1}{2}(d_i+d_j)$の両辺を2乗すると、$t_c$についての2次方程式となるので、解の方程式から導かれます。なお、解は2つあるのですが、+の方の解(大きい方の解)は粒子が貫通後に接触するまでの時間です。

2.2衝突後の速度の更新

衝突前後でも物体の重心は等速直線運動をする性質を利用して、重心系の速度とi,jの相対速度を利用して、衝突後の速度を算出します。
(ここではプログラムに合わせて説明していますが、参考文献(特にWikipedia)の記事の方が直感的な理解がしやすいです）

衝突前後で運動量が保存されるので、

m_iv_i+m_jv_j=m_iv_i'+m_jv_j'

となります。反発係数を$e$とすると、

e=-\frac{v_i'-v_j'}{v_i-v_j}

となるので、これらより、

v_i'=V-e\frac{m_j}{m_i+m_j}v_{ij}\\
v_j'=V+e\frac{m_i}{m_i+m_j}v_{ij}\\

ここで、

V=\frac{m_iv_i+m_jv_j}{m_i+m_j}

で、重心の速度を意味します。

なお、完全弾性衝突時($e=1$)の関係の図は下記のようになります。

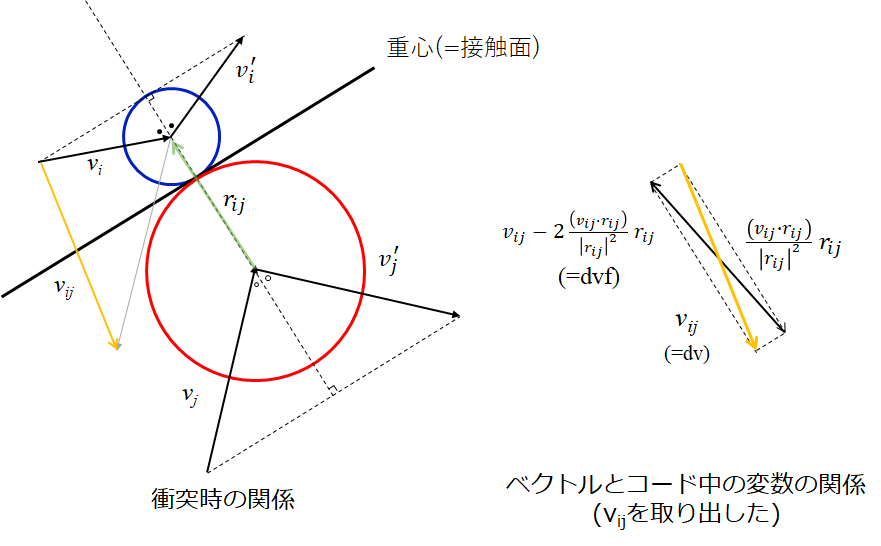
*dvfとdvは3章でのソースコード中の変数です。コードだとわかりにくい。。

#3. 実装 (thermosimのthermosim.py/def collideより)

3.1. 衝突判定

thermosim.py

    from scipy.spatial.distance import squareform,pdist
    # Find colliding particles
    D = squareform(pdist(self.r))
    ind1, ind2 = np.where(D < .5*np.add.outer(self.d, self.d))
    unique = (ind1 < ind2)
    ind1 = ind1[unique]
    ind2 = ind2[unique]

self.rとself.dにはそれぞれ座標と直径を収めたnp.arrayで、squareform(pdist(self.r))で現時点での粒子間の距離を、.5*np.add.outer(self.d, self.d)で粒子が接するときの距離を算出します。それぞれ、粒子の数をnとするとnxnのarrayを返します。
unique = (ind1 < ind2)としているのは、上三角の成分(対角は除く)のみが必要な情報なためです。

3.2. 衝突時の座標の算出

thermosim.py

            ru = np.dot(dv, dr)/ndv
            ds = ru + sqrt(ru**2 + .25*(d1+d2)**2 - np.dot(dr, dr))
            if np.isnan(ds):
                1/0

            # Time since collision
            dtc = ds/ndv

            # New collision parameter
            drc = dr - dv*dtc

dtcは2.1の$-t_c$と同じ意味かつ、同じ算出方法です。drcが衝突時の相対位置ベクトルのはず。

速度の更新

thermosim.py

            # Center of mass velocity
            vcm = (m1*v1 + m2*v2)/(m1+m2)

            # Velocities after collision
            dvf = dv - 2.*drc * np.dot(dv, drc)/np.dot(drc, drc)
            v1f = vcm - dvf * m2/(m1+m2)
            v2f = vcm + dvf * m1/(m1+m2)

dvfが何を意味するかは2章の衝突時の図を参照。

座標の更新

thermosim.py

            # Backtracked positions
            r1f = r1 + (v1f-v1)*dtc
            r2f = r2 + (v2f-v2)*dtc

これ、dtcでいいのか？ちょっと考え中です。

#参考文献

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up