大規模剛体球系の高速シミュレーション

　　
研究で多数の剛体球の高速シミュレーションが必要になったのですが、(プログラミング初心者としては)かなり難しい部分があったので書き残しておきたいと思います。

#1 剛体球のシミュレーションとは
##1.1 今回の設定
簡単のために、二次元系を考えます。つまり今回考える"球"は円板です。まず、鉛直方向に重力がかかっている状況を考えます。そして床面が高速で振動する箱を用意し、その中に$N$個の粒子を入れることにします。これらの粒子間の反発係数は$e$とし、粒子と壁の間の衝突は弾性衝突とします。このとき床面の振動によってエネルギーを得た粒子が飛び回るような状況になります。箱の上面は十分高く、天井の衝突は無視できるものとしましょう。また簡単のために、球の半径はすべて$r$とします。
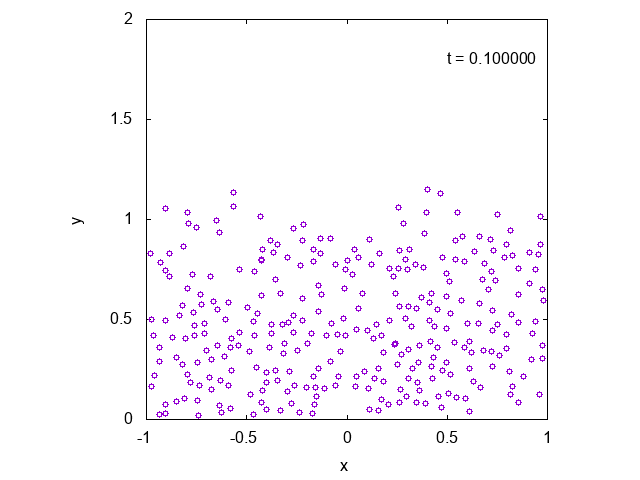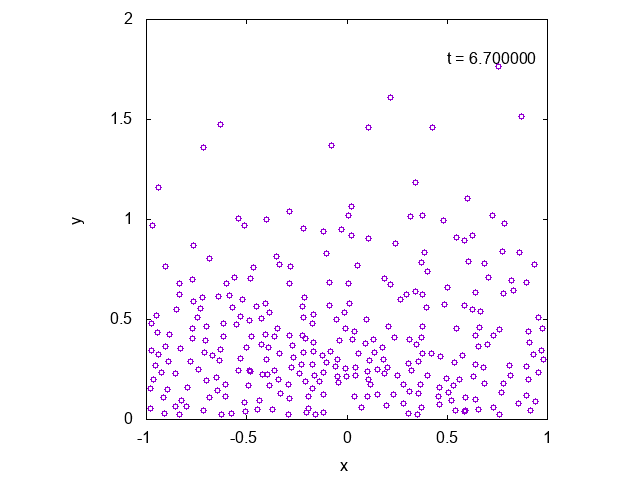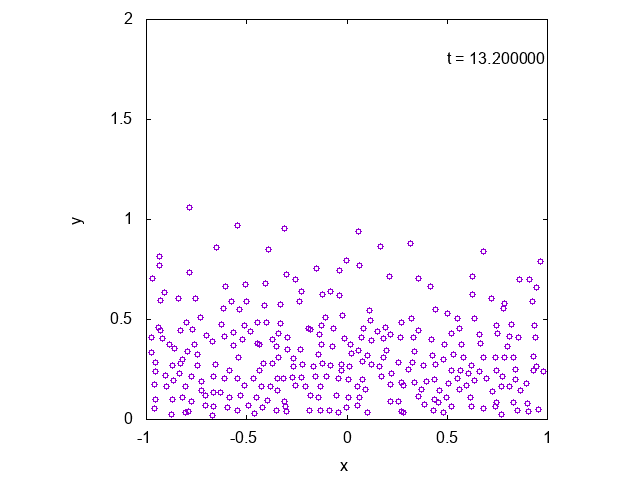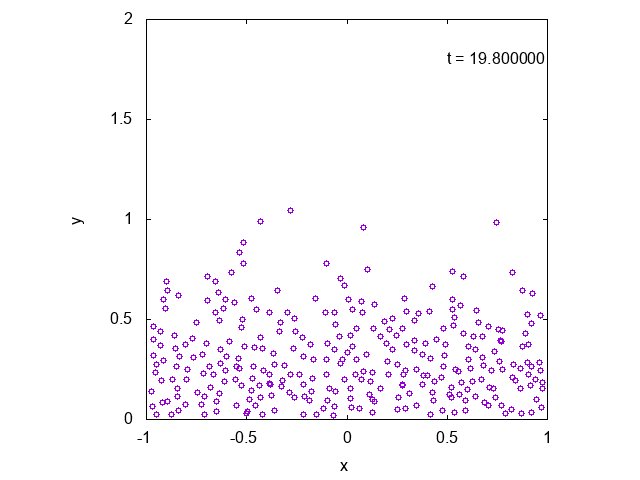
下の動画を見るとわかりやすいでしょう。

かなり状況が限られているように思えるかもしれませんが、より一般の場合に修正することも容易です。

##1.2 物理的意味
ここまでだと剛体球のシミュレーションを調べて何の意味があるのかわからないかもしれませんが、多数の剛体球系はたくさんの興味深い現象を示すことが知られています。斥力しか働かない剛体系において、固相-液相相転移(結晶化)が生じるということがAlderによって示されました(Alder転移)。また粉体の振る舞いを再現しているという点でも重要です。例えば砂時計や砂嵐などの現象も、(およそ)剛体球として扱うことが出来ます。

#2 剛体球シミュレーションの手法
剛体球のシミュレーションには、大まかに2つの手法があります。1つ目は時間刻みを指定して、少しずつ時間発展させるTime-Step型のもの。2つ目は粒子の衝突というeventに基づいて時間発展させるイベント駆動(Event-Driven)型のものです。
##2.1 Time-Step型シミュレーション
この手法については @NatsukiLab さんが大変わかりやすい解説をされています。
https://qiita.com/NatsukiLab/items/476e00fea40b86ece31f
方法としては極めて単純で、

1. 時間を少しだけ進める
2. 衝突している粒子を見つける
3. 衝突の処理
4. 1から3の繰り返し
   のみです。ただ @NatsukiLab さんも記事内で指摘されているように、高密度の系だと粒子が高速で振動するような不自然な振る舞いをすることがあります。タイムステップを十分細かくすればそれを回避することもできますが、そうすると計算量の問題も生じます。またペナルティ法ではばね定数のパラメータの調整なども必要になるでしょう(これは使ったことがないのでよくわかりませんが)。
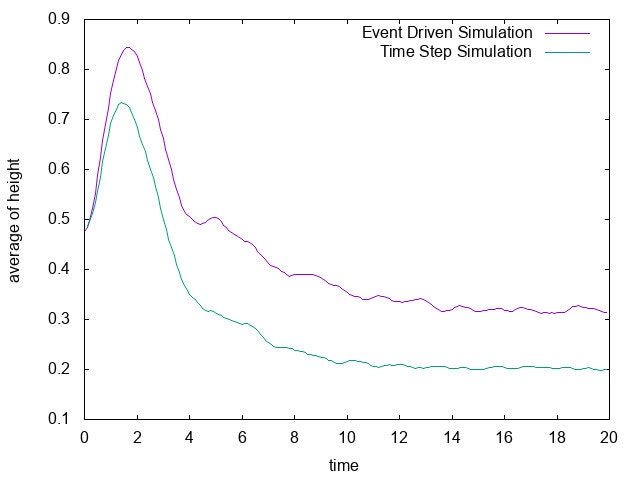
   実際に先ほどと同様の状況において、タイムステップ型のシミュレーションを行った結果を下に示します。最後の方では底面近くで凝縮しており、
   確かに先ほどとは様子が異なっていることが見て取れます。
   

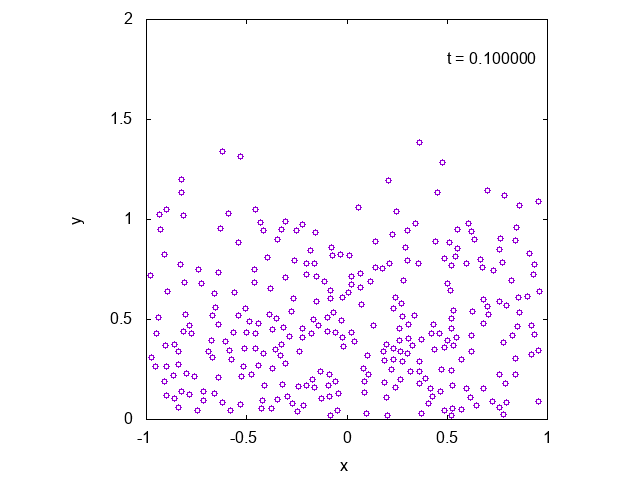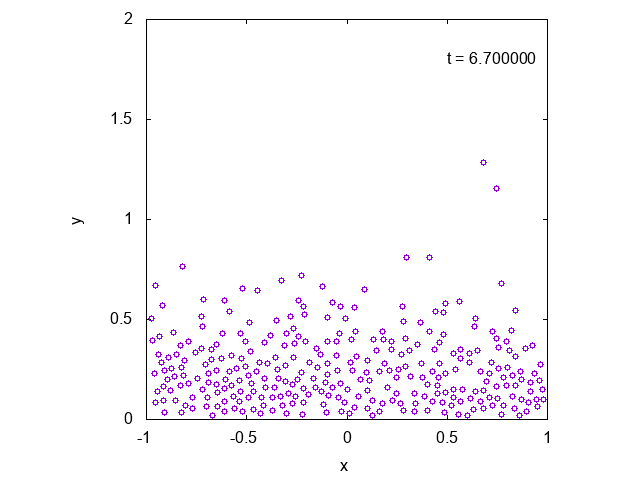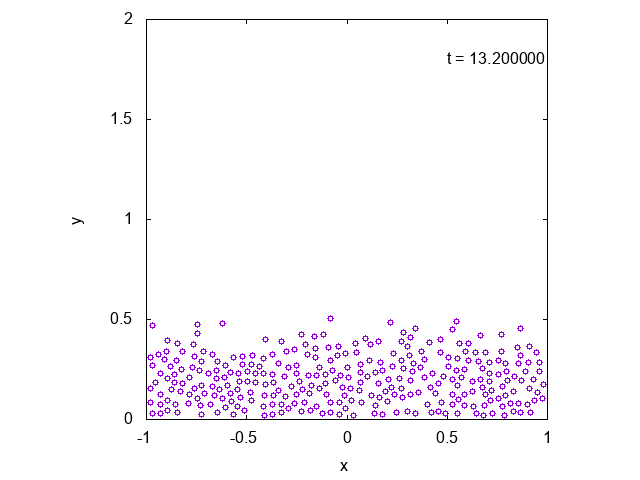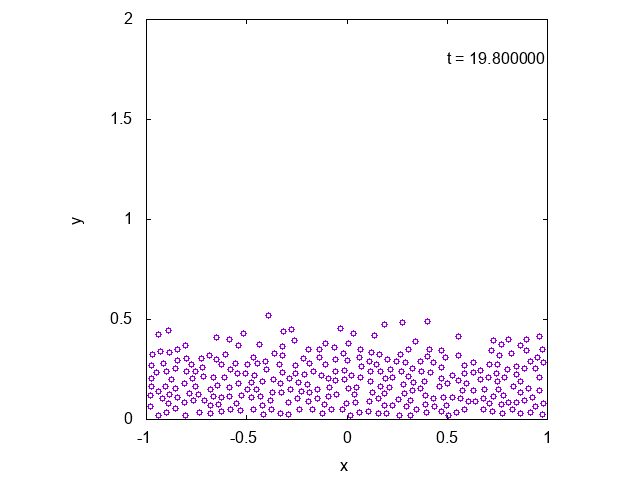
下には粒子の高さの平均値の時間変化をプロットしたものを示しました。明らかに異なる値に収束していることがわかります。

##2.2 Event-Driven型シミュレーション
高密度かつ大規模な系で威力を発揮するのがevent-driven型シミュレーションです。これは高速かつ厳密な結果を与えるという点で大きなメリットを持ちます。難点は実装が大変なことでしょうか。詳しい解説論文が名古屋工業大学の磯部先生によって書かれています。
https://ci.nii.ac.jp/naid/110006410561

#3 Event-Driven型シミュレーションの概要
##3.1 Event-Drivenとは
まずは、重力場中の2粒子$i,~j$が衝突するまでの時間を計算してみましょう。
時刻$t=0$において粒子$i,~j$の座標と速度はそれぞれ${\bf x} _ {i0},{\bf x} _ {j0}$と${\bf v} _ {i0},{\bf v}_ {j0}$で与えられるものとしましょう。
時刻$t$が経過したときのそれぞれの座標は、重力加速度のベクトル${\bf g}$を用いると以下のように書けます：

{\bf x}_i = {\bf x} _ {i0}+{\bf v} _ {i0} t +\dfrac{1}{2} {\bf g} t^2 \\
{\bf x}_j = {\bf x} _ {j0}+{\bf v} _ {j0} t +\dfrac{1}{2} {\bf g} t^2

このとき時刻$t$で衝突するという条件は$|{\bf x}_i-{\bf x}_j |= 2r$で表されます。
先ほどの式を代入すると、$t^2$の項が消えることに注意してください。頑張って計算すると、

t = -\dfrac{b_{ij}+\sqrt{b_{ij}^2-v_{ij}^2(r_{ij}^2-4r^2)}}{v_{ij}^2}

が得られます。ここで$b_{ij} = ({\bf x} _ {i0}-{\bf x} _ {j0})\cdot({\bf v} _ {i0}-{\bf v}_ {j0})$と$r_{ij} = |{\bf x} _ {i0}-{\bf x} _ {j0}|$を導入しました。

何が重要かというと、衝突にかかるまでの時間が完全に計算できてしまうという点です。
ここから、次のような手法が思いつきます：

1. すべての粒子について、他のすべての粒子との衝突までの時間を計算:$\mathcal{O}(N^2)$
2. 1.で得た最短の時刻まで時間を進める:$\mathcal{O}(N)$
3. 衝突する粒子のペアについて、衝突処理
4. 1から3を繰りかえす
   衝突処理については前述の @NatsukiLab さんの記事の「撃力法」を参考にしてください。また壁との衝突も簡単に含めることができます。このような「衝突」を指して、eventと呼ぶことにします。eventごとに時間を進めるため、event-drivenと言われます。

##3.2 Event-Driven型シミュレーションの特徴
この方法だと、数値誤差を除けば完全に正しい結果が得られることがわかります。また時間刻みに頭を悩ませる必要もありません。
ただこのままだと計算量が大きすぎる(1イベントあたり$\mathcal{O}(N^2)$)ことが問題です。考えたいのは大規模な系なので、高速化の必要があります。
この記事ではRapaportらのアイディアをもとに、1イベントあたりの計算量が$\mathcal{O}(\log N)$まで減ることを見ます。

#4 セルへの分割による高速化
ここでは分子動力学シミュレーションにおいて基本的な高速化手法であるセルへの分割を説明します。これはTime-Step型でも有効です。

##4.1 セルへの分割
まず高密度のシミュレーションで初めに気づくことは、基本的に自分の近くの粒子としか衝突しないということです。つまりある粒子について次に衝突する相手を探すとき、遠くの粒子まで考えるのは無駄になります。よってまず系をセルと呼ばれる小さい仮想的な箱に分割して、衝突相手は自分の所属する箱の近くからのみ探すことにします。下図で言うと、黒い粒子の衝突候補として太枠外を考慮する必要はないということです。これはセルの大きさが平均自由行程より十分大きければ問題ありません。枠外からの衝突には時間がかかるはずなので、それが(他粒子も含めた)全イベントの中で最短になるとは考えにくいです。ただセルの大きさは適切に選ぶ必要はあります。

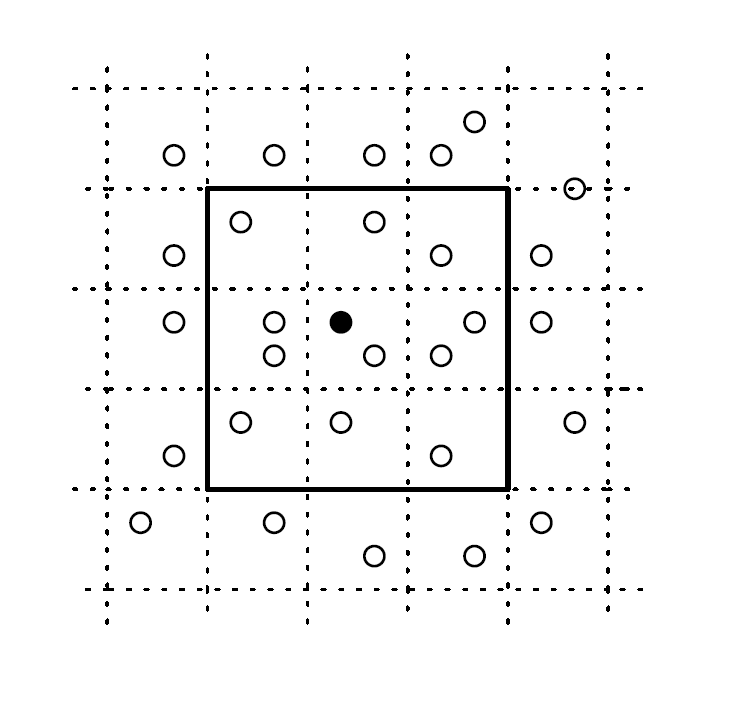
このようにすると、アルゴリズムは以下のように修正されます：

1. すべての粒子について、セルへの登録
2. すべての粒子について、近くの粒子との衝突までの時間を計算:$\mathcal{O}(N)$
3. 2.で得た最短の時刻まで時間を進める:$\mathcal{O}(N)$
4. 衝突する粒子のペアについて、衝突処理
5. 1から4を繰りかえす
   よって1イベントあたりの計算量は$\mathcal{O}(N)$になります。

##4.2 リンクリスト構造
先ほどの手法の2.において近くの粒子を捜索するとき、すべての粒子について近くかどうかを判定していると意味がありません。準備としてすべての粒子をセルに登録する必要がありますが、そのときリンクリスト構造を用いると便利です。セルごとに粒子をつなぐと考えれば大丈夫です。
実装を以下に示します。

#include <stdio.h>
#define N 300//粒子数
double Xmin = -1.0,Xmax = 1.0;//箱の左右の端
double Ymin = 0.0,Ymax = 1.0;//箱の上下の端,Ymaxはセルの登録のために必要

struct PARTICLE{//粒子を表す構造体
	double x,y,u,v;
	double next;
};

struct CELL{//セルを表す構造体
	int first;
	int last;
};
int N_cell_x = 8,N_cell_y = 8;//縦横のセルの分割数

void status_initialize(struct PARTICLE particle[N]);//粒子の初期化
void cell_register(struct PARTICLE particle[N],struct CELL cell[N_cell_x+1][N_cell_y+1]);//粒子のセルへの登録

int main(void){
	struct PARTICLE particle[N];
	struct CELL cell[N_cell_x+1][N_cell_y+1];
	status_initialize(particle);//位置や速度の初期化
	cell_register(particle,cell);//粒子をセルに登録する,nextofの初期化
     return 0;
}


void cell_register(struct PARTICLE particle[N],struct CELL cell[N_cell_x+1][N_cell_y+1]){
	int i,cell_x,cell_y,lastPrev;
	//initialize particle.next and cell
	for(i=0;i<N;i++){
		particle[i].next = -1;
	}
	for(cell_x = 1;cell_x <= N_cell_x;cell_x++){
		for(cell_y = 1;cell_y <= N_cell_y;cell_y++){
			cell[cell_x][cell_y].first = -1;
			cell[cell_x][cell_y].last = -1;
		}
	}

	double cell_length_x = (Xmax-Xmin)/(double)N_cell_x,cell_length_y = (Ymax-Ymin)/(double)N_cell_y;
	for(i=0;i<N;i++){
		cell_x = getcell_x(particle[i].x,cell_length_x);
		cell_y = getcell_y(particle[i].y,cell_length_y);
		lastPrev = cell[cell_x][cell_y].last;
		cell[cell_x][cell_y].last = i;
		
		if(lastPrev == -1){
			cell[cell_x][cell_y].first = i;
		}else{
			particle[lastPrev].next = i;
		}
	}
}

getcell_xやstatus_initializeは適当に設定する必要がありますが、長くなるので省略しました。
卑近な例で言うと、学生を研究室に配属させるイメージでよいと思います。学生が順に研究室(セル)に入っていき、先輩(自分よりラベルの小さい粒子)がいればその後輩(nextof)として自分を登録します。先輩がいなければ、自分が最古参(first)になります。いずれにせよ、自分が配属された時点では自分が新入り(last)になっているはずです。これをすべての粒子について行うと、各セルには最古参(first)を登録しておけばその後輩たち(nextof)をたどって各研究室(セル)の全メンバーをリストアップできます。
このセルへの登録を各イベントごとに実行すればokです。

#5 さらなる高速化
素朴に考えると、$\mathcal{O}(N)$のオーダーでも十分高速で、これ以上早くするのは難しそうです。しかし大規模な計算では不十分です。さらにうまい方法を使うと、よりオーダーを下げることができます。アルゴリズムを簡単に示すと以下の通りです：

1. 衝突する粒子ペアを平衡木から捜索：$\mathcal{O}(\log N)$
2. 衝突する粒子ペアのみ、時間を進める
3. 衝突処理
4. 衝突した粒子ペアについて近くの粒子との衝突までの時間を計算
5. 衝突した粒子ペアと衝突する予定の粒子がいたら、その粒子について衝突までの時間を再計算
6. 4.5で得た最短のイベントを用いて平衡木を更新
7. (セル外の粒子と衝突する可能性が生じる時刻になるたびセルの更新)
   このように、少し複雑になります。とくに面倒なのは平衡木がトーナメント型になっていることや、イベントが無効になること、粒子ごとに固有時間を設ける必要があることなどです。

コードは長くなってしまうのでgithubの1box.cを参照してください。単純にコンパイルし実行するだけで動きます。同じディレクトリに"gif.txt"と"plot.txt"を置いておくと、ターミナルから"gnuplot gif.txt"とコマンドを打てばgifファイルが生成されるようになっています。

https://github.com/yotapoon/demon
時間があればアルゴリズムの詳細についても追記します。またCBT_buildの実装などはかなり無理やりなので、もう少しうまく書けるという部分があれば教えてもらいたいです。