シグモイド関数とは：（超初級）Pythonでグラフを見てみる

シグモイド関数

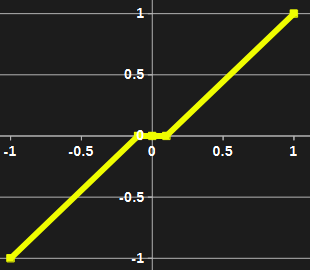
電子工作などで，ジョイスティックからの操作量を入力として値を取得したい．そんな時，不感帯を設定しておかないとレバーを中立にしているのに，じわじわと動いてしまう．しかたなく，下図のようなテーブル関数などを介して，操作量ｘが入ってきたら，操作量ｙを出力するようなプログラムを作成する．

このようなテーブル関数は，折れ点が存在している．
微分できない！これは，シミュレーションや組込み制御システム上，一時的なメモリの消費が大きくなったり，システムの微分方程式を解く上で問題となりえる．

そこで，登場するのが，『シグモイド関数』

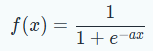
微分可能な関数で定義できると，演算処理の上でも利点だらけです．
計算速度も向上，メモリも節約，安定性も向上．

機械学習などで，この関数をそのまま利用できる場面も多く存在しますが，ゲインやオフセットなど若干修正を加えると，自分がやりたいことに柔軟に活用することができる．

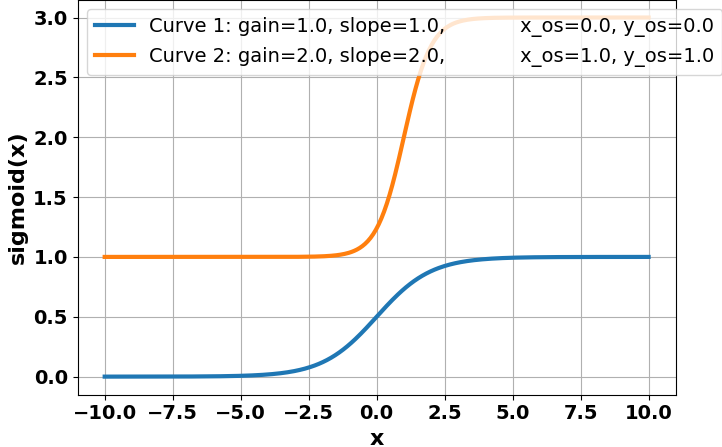
そこで，Pythonを用いて，ゲインやオフセットを変えたときにどんなグラフになるのかをさっと眺めるスクリプトを示しておきます．

任意の信号をシグモイド関数で変換したら，それは，自分が思っていたような変換であるかどうかをこのようなグラフで事前に確認するように心がけたい．

sigmoid_dialog2.py

import numpy as np
import matplotlib.pyplot as plt
import tkinter as tk
from tkinter import simpledialog

# シグモイド関数の定義（パラメータ付き）
def sigmoid(x, gain=1, slope=1, x_os=0, y_os=0):
    return gain / (1 + np.exp(-slope * (x - x_os))) + y_os

# ダイアログでパラメータを取得
def get_parameters():
    root = tk.Tk()
    root.withdraw()  # メインウィンドウを非表示

    curves = []
    num_curves = simpledialog.askinteger("入力", "プロットするシグモイド曲線の数を入力してください：")

    for i in range(num_curves):
        gain = simpledialog.askfloat(f"Curve {i+1}", "ゲイン（gain）を入力してください：", initialvalue=1.0)
        slope = simpledialog.askfloat(f"Curve {i+1}", "傾き（slope）を入力してください：", initialvalue=1.0)
        x_os = simpledialog.askfloat(f"Curve {i+1}", "Xオフセット（x_os）を入力してください：", initialvalue=0.0)
        y_os = simpledialog.askfloat(f"Curve {i+1}", "Yオフセット（y_os）を入力してください：", initialvalue=0.0)
        curves.append((gain, slope, x_os, y_os))

    return curves

# メイン処理
def plot_sigmoid_curves():
    x = np.linspace(-10, 10, 400)
    curves = get_parameters()

    plt.figure(figsize=(10, 6))
    for i, (gain, slope, x_os, y_os) in enumerate(curves):
        y = sigmoid(x, gain, slope, x_os, y_os)
        plt.plot(x, y, label=f'Curve {i+1}: gain={gain}, slope={slope},\
            x_os={x_os}, y_os={y_os}', linewidth=3)
        
    # フォントサイズの調整
    plt.title('Multiple Sigmoid Curves', fontsize=18, fontweight='bold')
    plt.xlabel('x', fontsize=16, fontweight='bold')
    plt.ylabel('sigmoid(x)', fontsize=16, fontweight='bold')
    plt.xticks(fontsize=14, fontweight='bold')
    plt.yticks(fontsize=14, fontweight='bold')
    plt.grid(True)
    plt.legend(fontsize=14, loc='upper left')
    plt.show()

plot_sigmoid_curves()