本記事では,GPSデータや地図,移動経路特定に関わる際に重要な,「マップマッチング」について紹介します.
マップマッチングとは
マップマッチングとは,記録されたGPSデータをユーザが移動した経路を推測する操作のことです.
例えば,赤いGPS点が記録されたとします.このとき,移動者は青線で示す経路を移動したと考えられます.このようにGPSデータを道路にマッチングさせる操作を,マップマッチングといいます.
 1
1
マップマッチングにおけるError
GPS測位点を地図上にマッチングさせる際,GPSデータには「エラー」があることに注意する必要があります.GPSデータには以下の2種類のエラーがあります1.
- 測定誤差:GPS測位点が,真の位置情報からずれること
- サンプリング誤差:記録の間で位置情報が失われること
これらの誤差があるGPSデータに対して,様々なマップマッチングアルゴリズムが考案されています.
マップマッチングアルゴリズム
マップマッチングには,以下の4つのアプローチがある2と言われています.
- 幾何学的アプローチ
- 位相的アプローチ
- 確率的アプローチ
- 他の発展的な技術を用いたアプローチ
| アルゴリズム | 概要 |
|---|---|
| 幾何学的アルゴリズム | 交差点や道路リンクとの距離といった,幾何学的距離に基づいてマッチングする手法. |
| 位相的アルゴリズム | 道路とGPSデータの交差角度などを用いて,道路リンクの接続性や連続性を考慮したマッチング3. |
| 確率的アルゴリズム | 位置情報の誤差領域を近似したアルゴリズム. |
| その他の発展的手法 | 複数の手法を組み合わせたり,状態空間モデル(Kalman filter, Particle filterなど)やファジー理論といった高度な理論が用いられることも多い. |
①幾何学的マップマッチング(Geometric Analysis)
文字通り,道路ネットワークの「幾何的な」情報を用いたアルゴリズムです.最も単純でシンプルな探索アルゴリズムです.GPS位置情報を,道路セグメントの"node"や"shape point"にマッチングさせます.
ここで,
- node:道路の端点 ←簡単に言うと「交差点」
- shape point:道路曲線や折れ線の途中の形状点(道路の曲がりや形状を正確に表現するための中間点) ←簡単に言うと「道路リンク」
を指します.幾何学的マップマッチングでは,マッチング対象によって以下の3種類があります.
| マッチング手法 | 概要 |
|---|---|
| point-to-pointマッチング | 各測位点を最も近い交差点(ノード)に割り当てる手法. |
| point-to-curveマッチング | 各測位点を最も近い道路リンク(エッジ)に割り当てる手法. |
| curve-to-curveマッチング | 測位点を結んだ経路に最も近い経路を選択する手法. |
では,これら3つのマッチング手法について1つずつ見ていきましょう.
poin-to-point マッチング
GPS測位点を,道路ネットワーク上の最も近いノード(交差点)にマッチングさせる手法です.アルゴリズムの手順としては,
- 測位点とすべてのノードとの距離を計算
- 測位点を最も距離の短いノードにマッチング
- すべての測位点に対して上記の操作を行う
- ダイクストラ法などを用いて,マッチングされた交差点を通る最短経路を求める.←これが,マップマッチング結果となる!
point-to-point マッチングでは,ノード(交差点)が多いネットワークほど正確にマッチングさせることができます24.逆に,交差点の少ない長い道路を持つネットワークの場合,測位点は道路リンクの端点のどちらかにマッチングされることになるため,マッチングに誤差が生じやすくなります2.
point-to-point マッチングは最寄りのノードに割り当てるアルゴリズムのため,ノード(交差点)数$N$に応じた$O(N)$の計算量がかかります.$k$次元空間を効率的に探索する二分探索木であるkd木 (kd-tree)を用いると,最寄りノード探索を$O(\log n)$まで高速化することができ,大規模データにも対応可能になります.
point-to-curve マッチング
point-to-curve マッチングは,測位点を道路ネットワーク上の最も近いリンク(道路)にマッチングさせる手法です.アルゴリズムの手順としては,
- 測位点とすべてのリンクとの距離を計算
- 測位点を最も距離の短いリンクにマッチング
- すべての測位点に対して上記の操作を行う
point-to-curve マッチングは,point-to-point マッチングとは対照的に,ノード(交差点)が多いネットワークほど誤りやすいです.
ノード数が多く,1本あたりの道路リンクの長さが短いほど,誤った道路リンクにマッチングさせてしまう可能性があるのです.
point-to-point マッチングやpoint-to-curve マッチングは,外れ値に敏感で,直前の位置情報を用いないというデメリットがあります.
curve-to-curve マッチング
上記で扱った2つのマッチング手法より精度がよい手法4として,curve to curve マッチングがあります.アルゴリズムの手順4としては,
- point to point マッチングにより,測位点をマッチングする候補ノードを探索
- 候補ノードを繋ぎ,候補リンクを作成
- 候補ノードを結び,候補経路を作成 ←ポイントはココ!!
- 測位点を結び,その軌跡の距離の和を計算
- すべての経路候補のうち,最も測位点の経路距離と近いもの
曲線間の距離の計算方法として,Fréchet distance(フレシェ距離)と呼ばれる手法などがあります.
幾何学的マップマッチングは,簡単に実装でき,計算時間が速いのが特徴です.
一方,幾何学的なマップマッチングはデメリットもあります.
例えば,一直線の長い道路上の点は,すべて道路の端点のみにマッチングされることになります.また,前後の繋がりを考慮していないため,離れた道路にマッチングされてしまう可能性もあります.
➁位相的マップマッチング(Topological Analysis)
道路ネットワークの「位相的な」繋がりに着目したアルゴリズムです.
例として,隣接関係(ポリゴンの場合),接続関係(線の場合),包含関係(点とポリゴンの場合)などがあります.
- 道路の曲率(曲がり方)
- 道路の接続関係
などの道路ネットワークの位相的特徴と車両の軌跡から,マップマッチングアルゴリズムを開発した研究もおこなわれています.
幾何学的マップマッチングでは距離を基準としていましたが,位相的マップマッチングでは「道路の繋がり」を重視しているのです!
位相的マップマッチングについては,以下の資料および,それをもとにした以下のスライドが非常にわかりやすくまとめられています.
-
羽藤英二教授『ネットワーク行動学 -都市と移動-』
マップマッチングはp84-106.
③確率的マップマッチング
上記の2つのアルゴリズムでは,各GPS測位点に対して,マッチングする交差点や道路リンクは「一意」に定まっていました.しかし,確率的マップマッチングでは,これらを「確率的」に決まるものとするのです.
その代表例として,HMM(隠れマルコフモデル)を用いたアルゴリズムが挙げられます.
HMM (Hidden Markov Model, 隠れマルコフモデル)
Microsoftの研究者であるNewson and Krumm5によって提案されたマップマッチングアルゴリズムです.ValhallaやMapbox, GraphHopperといった現在のマップマッチングサービスやUberなど,幅広く使われています.
隠れマルコフモデルとは,「ある状態から別の状態への遷移の尤もらしさ」を記述するモデルです.
HMMでは,Uターンやループのような極端に可能性の低い経路にマッチングされることを避けることができます.
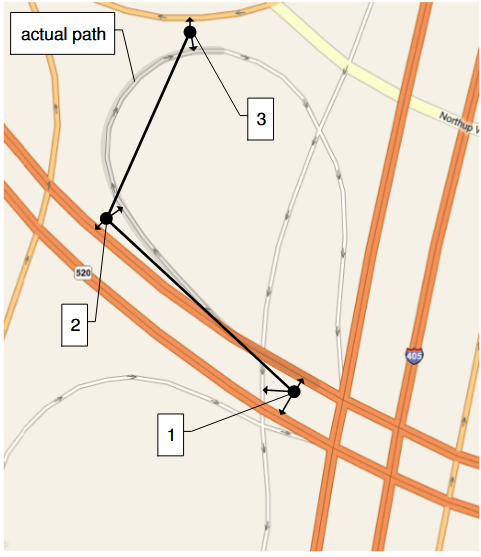
例えば,下図の黒い点にGPSが記録されたとします.(数字は順番)
単純に一番近い道路(または交差点)に割り当てるだけでは,実際の経路(上図だと曲線部分)が正しく判定されません.
これは,各GPS位置情報のマッチングを「別々」に行っており,前後の「繋がり」を全く考慮できていないためです.
そこで,一つ前の状態からの「遷移確率」をモデル化したHMMを活用したマップマッチングが行われています.(Newson and Krumm (2009)5がその先駆的研究)
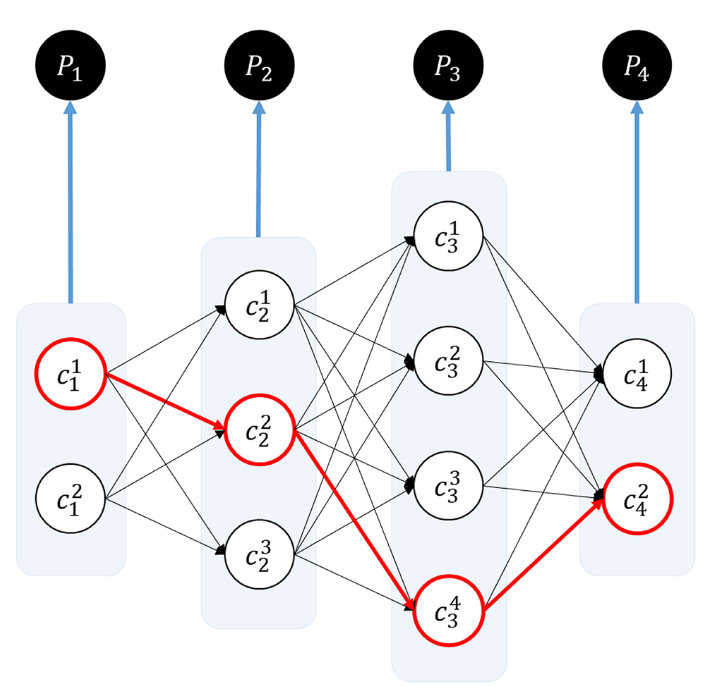
例えば,下の黒点にGPSデータが記録されたとします.
 1
1
このとき,各GPS測位点$P_i$は,候補道路リンク$c_i^j$を持っています.これらの構造は以下のように簡略化でき,尤もらしい経路を判定しようというものです.
HMMを活用したマップマッチングアルゴリズムの手順
- GPSデータの測位点:$z_t$
- 候補道路位置:$x_t$
- GPS誤差の標準偏差:$\sigma$
HMMを用いたマップマッチングの流れは以下の通りです.
1.初期状態確率
また,初期状態確率 $\pi_i\quad (i=1,...,N_r)$を定義します.$\pi_i$は,「移動開始時$t=1$において,道路$i$にいる確率」です.
$\pi_i$として一様分布を仮定する場合や,最初の測定位置を用いて,
\pi_i = p(z_1|r_i)
とする場合5もあります.
2.GPSの測定誤差の仮定
実際の位置(道路)が$r_i$であるときに,位置情報が$z_t$に記録される確率$p(z_t|r_i)$が,
p(z_t|r_i) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left[{-\frac{1}{2}\left(\frac{\|z_t-x_{t,i}\|}{\sigma}\right)^2}\right]
で表されると仮定します.
$p(z_t|r_i)$は平均$x_{t,i}$,分散$\sigma^2$の2次元正規分布.すなわち,GPS測定位置と真の位置の測定誤差$|| z_t-x_{t,i} ||$を「正規分布」で仮定しているのです.
地理空間の情報を扱う際は,距離には大円距離 (Great cicle distance)を用いることが多いです.大円距離とは,地球のような球体の表面上の2点間距離(最短の弧の長さ)を指します.
3.遷移確率
次に,測位点$z_t$から次の測位点$z_{t+1}$での遷移確率について考えます.
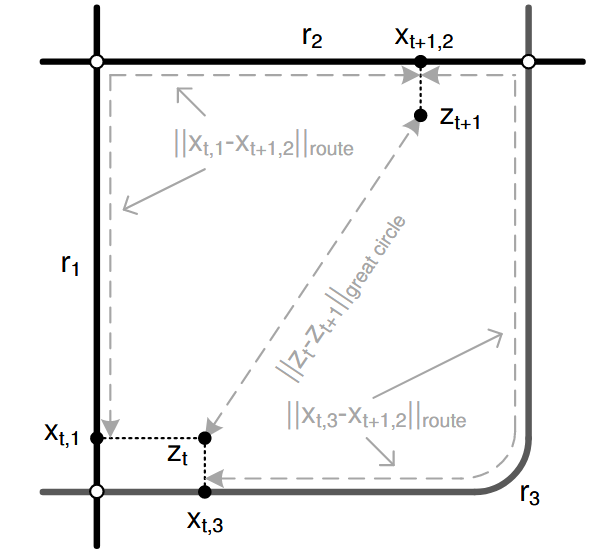
まず下図のように,GPS測定点$z_t$と候補道路セグメント$r_i$があるとします.
$z_t$から道路セグメント$i$上の最近傍点を$x_{t,i}$とします.次の測位点 $z_{t+1}$についても同様に候補点$x_{t+1,j}$があります.
ここで,正しくマッチングされた経路は当然,短い経路かつGPS測定点に近いはずです.
- $x_{t,i}$と$x_{t+1,j}$間の道路距離:$|| x_{t,i}-x_{t+1,j}||_\text{route}$
- GPS測定点$z_t$と$z_{t+1}$間の大円距離:$|| z_t - z_{t+1} ||_{\mathrm{great\ circle}}$
の差に着目します.この距離差が大きくなるほどマッチング確率は下がる様子を,HMMでは文献5の実験結果より,指数減衰:
p(d_t) = \frac{1}{\beta} e^{-d_t/\beta}
ただし,$d_t$は,routeにおける真の道路セグメントを$i*,j^*$として,
d_t = \left| \| z_t - z_{t+1} \||_{\mathrm{great\ circle}}- \| x_{t,i*}-x_{t+1,j*}\||_\text{route} \right|
としています.
このようにして,HMMでは,
- 初期状態確率:どこからスタートするか
- 観測確率:GPS 誤差を考慮して候補道路を評価
- 遷移確率:道路ネットワーク上での移動の自然さを評価
の3つを組み合わせ,Viterbiアルゴリズムなどを用いて最尤経路を推定します.
Viterbiアルゴリズムとは,動的計画法 (Dynamic Programming)を用いて,尤もらしい状態列を求めるもので,全探索より効率的で高速なのが特徴です.
④その他の発展的な技術を用いたマップマッチング
その他の指標として,機械学習などで用いられるKalman filterやParticle filter,ファジー理論を用いた手法などがあります.いずれも誤差のある観測値に対して扱われる手法です.
また,複数の手法を組み合わせたマップマッチングも行われています.
マップマッチングの実用
実用上におけるマップマッチングは,リアルタイム(オンライン)とオフラインがあります.
| アルゴリズム | 概要 | 利用例 |
|---|---|---|
| リアルタイム・マップマッチング | その場で即座に地図上の道路や経路にマッピングする方式 | カーナビや地理情報アプリの現在地表示 |
| オフライン・マップマッチング | 移動データを全て収集した後に、まとめて道路上にマッピングする方式 | 交通流量や移動経路の分析など |
一般に,リアルタイム・マップマッチングの方が即時性を求められるため,精度は低く,シンプルなアルゴリズムを使うことが多いという特徴があります.
OSRM (Open Source Routing Machine)
OSRM (Open Source Routing Machine)は,オープンソースのルーティングエンジン(経路探索ソフトウェア)です.OpenStreetMap (OSM) の地図データを利用して動作します.
Newson and Krumm5のアルゴリズムも一部応用されています.
OSRMでは,Contraction Hierarchies (CH)という最短経路探索を高速化するためのグラフ前処理手法が用いられています.このアルゴリズムについては,私も勉強中です.
まとめ
本記事では,古典的なものから発展的なものまで網羅的にマップマッチング手法を紹介しました.実務においては,複数の手法を組み合わせることも多くあります.
また,マップマッチングにおいては,アルゴリズム同士の精度や優劣を比較するということは一筋縄ではいきません.なぜなら,真の位置情報がどこかなどわからないからです.そのため,通常は仮想的なGPSデータに対して,マッチング結果を比較します.
参考文献
-
羽藤英二教授『ネットワーク行動学 -都市と移動-』
マップマッチングはp84-106. -
mapbox の Map Maching API を使ってGPS誤差を補正しよう!
マップマッチングAPIについても紹介されています.
-
Saki, S., & Hagen, T. (2022). A practical guide to an open-source map-matching approach for big GPS data. SN Computer Science, 3(5), 415. ↩ ↩2 ↩3 ↩4
-
Quddus, M. A., Ochieng, W. Y., & Noland, R. B. (2007). Current map-matching algorithms for transport applications: State-of-the art and future research directions. Transportation research part c: Emerging technologies, 15(5), 312-328. ↩ ↩2 ↩3
-
橋口 剛,瀬谷 創,安田 昌平,井料 隆雅 (2022):隠れマルコフモデルに基づくマップマッチングの適用性の検証,土木学会論文集D3 (土木計画学), Vol.77, No.5. ↩
-
Paul Newson and John Krumm (2009):Hidden Markov Map Matching Through Noise and Sparseness, GIS '09: 17th SIGSPATIAL International Conference on Advances in Geographic Information Systems ↩ ↩2 ↩3 ↩4 ↩5 ↩6 ↩7