はじめに
以前、「機械学習の分類」で取り上げたアルゴリズムについて、その理論とpythonでの実装、scikit-learnを使った分析についてステップバイステップで学習していく。個人の学習用として書いてるので間違いなんかは大目に見て欲しいと思います。
これまで、2クラス分類問題として、単純パーセプトロン、ロジスティック回帰、そしてサポートベクターマシン(基本編・応用編)を扱ってきました。
ただ、あくまで2クラスの分類だったので、それらを多クラスの分類に拡張することを考えてみます。
最初ロジスティック回帰とサポートベクターマシンの多クラス化を一緒に書いてしまおうと思っていたんですが、意外と奥が深かったのと、意外ときちんと書いていないサイトも多く、理論的な背景だけで1記事になってしまいました。例によって参考になったのは下記のサイト。ありがとうございました。
- 機械学習 第7回 分類(多クラス分類)→大学の講義資料ですかね?
- 【翻訳】scikit-learn 0.18 User Guide 1.12. 多クラスアルゴリズムと多ラベルアルゴリズム
- One-vs-RestとOne-vs-Oneを実装してみた
- 多クラス分類ロジスティック回帰の実装
2クラス分類→多クラス分類への拡張
$N$種類の特徴量に対し、出力$y$で$c$種類の分類を行うことを考えます。例えば(リンゴ|ミカン|バナナ)を分類するとか0〜9の数字を分類するとかそういう類のやつですね。アルゴリズム自体が多クラス分類に対応しているものもあるんですが、ロジスティック回帰やサポートベクターマシンなど2クラス分類器をこの分類問題に対応させるためのアプローチとしては、以下の手法が代表的です。
- One vs Rest(All)
- One vs One
- 多クラスソフトマックス(softmax)
順番に考えていきましょう。
One-vs-Rest(All)
One-vs-Rest(One-vs-Allと記述される場合もある)は、その名の通り、あるクラスと残りのクラスに分割して分類するやり方です。
例としてリンゴ、ミカン、バナナの3クラスを分類するために、下図のように(リンゴ-その他)、(ミカン-その他)、(バナナ-その他)という3つの分類器を作ります。
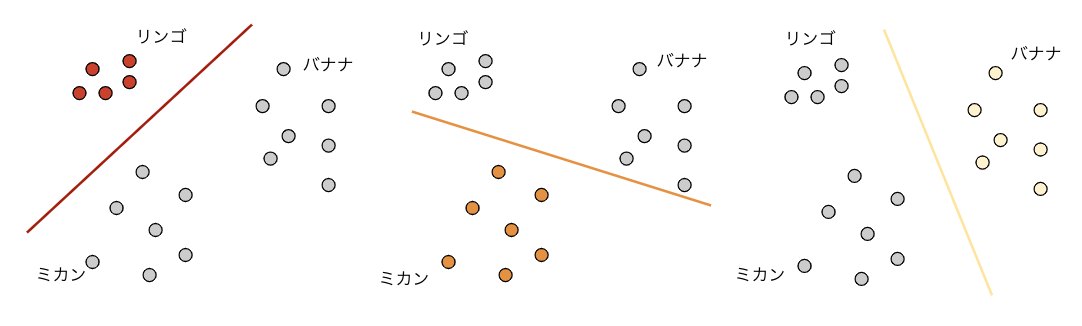
実際には各分類器の境界で例えばリンゴともバナナともとれる領域があるんですが、そういう場合は各分類器の出力の強さなどを使ってどちらかに決めるなどの処理が必要になります。
クラスの数だけ分類器を用意すればいいので計算量は次に説明するOne-vs-Oneよりは少なくてすみます。
One-vs-One
One-vs-Restとは違い、任意の2つのクラスを選んで2クラス分類します。組み合わせの数はクラス数を$n$とすると、$ n C_2$種類の分類器が必要になります。
例えば10クラスを分類する場合、One-vs-Restでは10種類の分類器があれば大丈夫でしたが、One-vs-Oneになると、$_{10}C_2=45$種類の分類器が必要になってしまいます。最終的な分類は各分類器の多数決で決めます。
線形回帰ではなく、モデルにカーネル法を使った場合はこちらを使うことがあるみたいです。
実際に、scikit-learnのドキュメントを参照すると以下のような扱いになっているようです。
- sklearn.linear_model.LogisticRegression→One-vs-Rest
- sklearn.svm.SVC→0.19まではOne-vs-One、それ以降はOne-vs-Rest
- sklearn.svm.LinearSVC→One-vs-Rest
多クラスソフトマックス
多クラスソフトマックスは、最近ではニューラルネットワークでよく用いられます。モデルの出力に対し、どのクラスが一番可能性が高いかという数値をソフトマックス関数を用いて学習します。
ソフトマックス関数について説明する前に、One-hot Encodingについて先に説明します。
One-Hot Encoding
One-Hot Encodingは端的に言えば、ひとつだけが1であとは0というベクトルを指します。例を出すと、ある特徴量が
| 果物 |
|---|
| リンゴ |
| ミカン |
| リンゴ |
| バナナ |
| となっていたとします。これを下記のように書き換えます。 |
| 果物_リンゴ | 果物_ミカン | 果物_バナナ |
|---|---|---|
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 0 | 1 |
このような形にすることで、先ほどあげたOne-vs-Rest(One)の分類に分割できることと、次に述べるソフトマックス関数の計算に持って行きやすいという利点があります。また、Pandasのget_dummies()関数やsikit-learnのOneHotEncoderクラスが使えます。
ソフトマックス関数
ソフトマックス関数は、複数の出力を合計が1(100%)になるような確率分布に変換してくれる関数です。ソフトマックス関数は下のような形をしています。
y_i=\frac{e^{x_{i}}}{\sum_{j=1}^{n}e^{x_{j}}} \\
\sum_{i=1}^{n}y_i=1
$y$は$n$次元のベクトルで、出力も同様です。先ほどの例で、(リンゴ,ミカン,バナナ)=[3,8,1]と出力されたとすると、ソフトマックス関数の出力は[0.7,99.2,0.1]となり、ミカンの可能性が一番高いことになります。
ちなみに2クラス分類は、上の式でn=2なので
\begin{align}
y_1&=\frac{e^{x_{1}}}{e^{x_1}+e^{x_2}} \\
&=\frac{\frac{e^{x_{1}}}{e^{x_{1}}}}{\frac{e^{x_{1}}}{e^{x_{1}}}+e^{x_2-x_1}} \\
&=\frac{1}{1+e^{x_2-x_1}}
\end{align}
となります。これはシグモイド関数そのものです。
ソフトマックス関数の微分
ソフトマックス関数の微分は
\dfrac{\partial y_i}{\partial x_j}=
\begin{cases}y_i(1-y_i)&i=j\\-y_iy_j&i\neq j\end{cases}
です。
ソフトマックス関数による多クラス分類
クラス数が$c$、入力が$\boldsymbol{x}=(x_0, x_1,\cdots,x_n)$とする($x_0$はバイアス)。パラメータを$(n+1)$×$c$の大きさを持った$\boldsymbol{W}$とする。
\boldsymbol{z}=\boldsymbol{W}^T\boldsymbol{x}
をモデルとして$\boldsymbol{W}$を最適化します。
そのためには、ロジスティック回帰と同じように、**クロスエントロピー誤差関数$E$**を求めます。尤度関数を$l$とすると、$l$は全てのクラス、全てのサンプルに対する確率分布で表すことができる。$i$番目のサンプルにおけるクラス$j$のソフトマックス関数の出力を$\varphi_{ij}^{t_{ij}}$とすると、
l=\prod_{i=1}^{n}\prod_{j=1}^{c}\varphi_{ij}^{t_{ij}}
となる。尤度を最大化したいのですが、$l$の対数をとり、-1をかけた関数をクロスエントロピー誤差関数とし、
\begin{align}
E&=-\log(l) \\
&=-\log\left(\prod_{i=1}^{n}\prod_{j=1}^{c}\varphi_{ij}^{t_{ij}}\right) \\
&= -\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{c}t_{ij}\log\varphi_{ij}
\end{align}
が損失関数となる。損失関数の微分は、
\begin{align}
\frac{\partial E}{\partial w} &= -\frac{1}{n}\sum_{i=0}^n(t_{il}-\varphi_{il})x_{ij} \\
&=-\frac{1}{n}\boldsymbol{x}^T(\boldsymbol{t}-\phi)
\end{align}
となります。(計算省略)
あとは、$E$を最小化するために勾配法を使えばパラメータ$\boldsymbol{W}$を求めることができます。
まとめ
2クラス分類を多クラス分類へ拡張する方法についてまとめました。1つは2クラス分類を単純に繰り返す方法。もう一つはソフトマックス関数を使い、クラスごとの確率分布を求める方法でした。
探し方が悪かったのか、あまりこの辺の方法を詳しくまとめてるページが少なかったので時間がかかったのとソフトマックス関数を使った分類はかなり複雑でした。
次回以降、Pythonのコードに落として行きたいと思っています。