はじめに
以前、「機械学習の分類」で取り上げたアルゴリズムについて、その理論とpythonでの実装、scikit-learnを使った分析についてステップバイステップで学習していく。個人の学習用として書いてるので間違いなんかは大目に見て欲しいと思います。
前回、サポートベクターマシンの基本的なところについて書きました。前回は、ハードマージンと言って正例と負例がちゃんと分離できるSVMを扱いましたが、今回は
- ソフトマージン(ノイズの混ざった分類)
- カーネル法とカーネルトリック(線形分離不可能な問題)
について言及していこうと思います。
ソフトマージンSVM
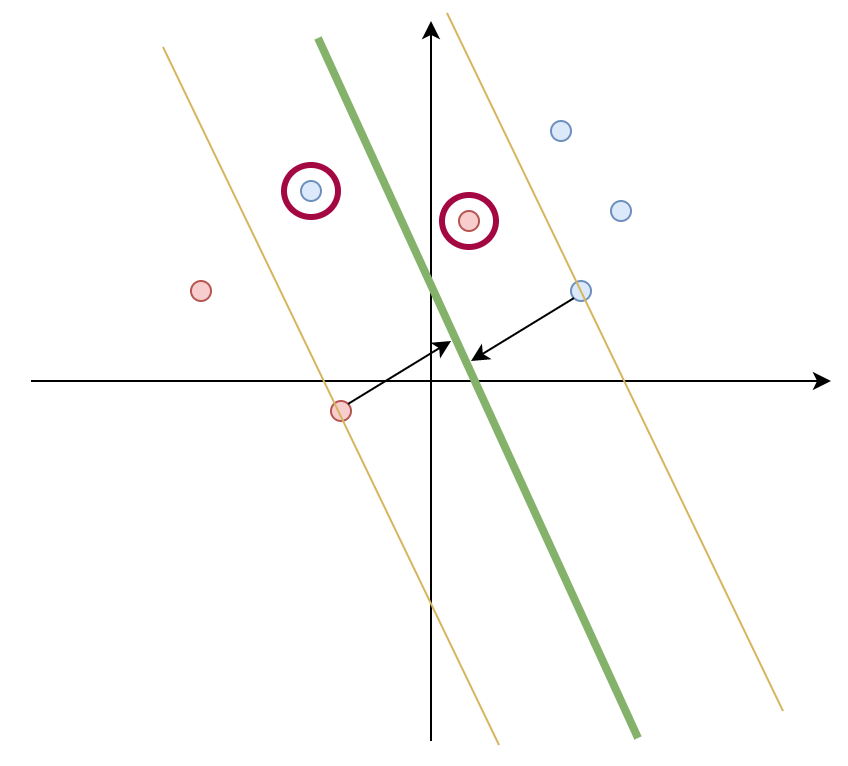
前回と違って、下図のような赤丸と青丸が微妙に分離できない例を考えます。
その前に復習
ハードマージンSVMの式はパラメータの集合を$w$としたときに、 $$ \frac{1}{2}|w|^2$$を$$ t_n(\boldsymbol{w}^Tx_n+w_0) \geq 1$$という制約条件化で最小化するという問題でした。ソフトマージンはこの制約条件を緩めた問題に変えます。
制約条件の緩和
条件緩和のために、スラック変数$\xi$とパラメータ$C$を導入します。スラック変数は、サポートベクターと境界線でどの程度誤差を許容するかという変数のことで、$C(>0)$は制約条件の厳しさを表します。これらを導入すると上に書いた解くべき問題が以下のように変わります。
\frac{1}{2}|w|^2+C\sum_{i=1}^{N}\xi_i \\
t_n(\boldsymbol{w}^Tx_n+w_0) \geq 1-\xi_n \\
\xi_n \geq 0
$C$と$\xi$の関係ですが、$C$が大きくなると$\xi$が小さくなければ最小化できず、$C$が小さければ$\xi$がある程度大きくても最小化できるということを意味します。$C$が無限大では、$\xi$がゼロしか許容できない(=マージン内にデータを許容しない)のでこれはハードマージンSVMと同じになります。
ラグランジュ未定乗数法による解
ハードマージンのときと異なり、制約条件が2つに増えたため、ラグランジュ乗数も$\lambda$と$\mu$の2つにします。
L(w,w_0,\lambda, \mu)=\frac{1}{2}|w|^2+C\sum_{i=1}^n\xi_i-\sum_{i=1}^{N}\lambda_i \{ t_i(\boldsymbol{w}^Tx_i+w_0)+\xi_i-1\}-\sum_{i=1}^n\mu_i\xi_i
これを$w$、$w_0$、$\xi$について偏微分し、それぞれゼロとおくと、
w=\sum_{i=1}^n\lambda_it_ix_i \\
\sum_{i=1}^n\lambda_it_i=0 \\
\lambda_i=C-\mu_i
を得ることができ、ラグランジュ関数に代入すると、
L(\lambda)=\sum_{n=1}^{N}\lambda_n-\frac{1}{2}\sum_{n=1}^{N}\sum_{m=1}^{N}\lambda_n\lambda_mt_nt_mx_n^Tx_m
となり、これはハードマージンの時と全く同じ式になります。ただし、制約条件が
\sum_{i=1}^n\lambda_it_n=0 \\
0 \leq \lambda_i \leq C
となります。こちらもハードマージンと同様SMOを使ってパラメータを求めることが可能です。(今回は省略)
カーネル法とカーネルトリック
以下のようないかにも直線で分離できなそうな例を考えてみます。
こういう形になっている場合は、2次元→3次元のように、より高次元の空間に点を動かしたうえで平面分離するということをやります。高次に変換する方法をカーネル法と呼び、変換するための関数をカーネル関数と呼びます。
基底関数
あるデータ列$\boldsymbol{x}=(x_0, x_1, \cdots, x_{n-1})$を射影したデータ列を$\boldsymbol{\phi}=\{ \phi_0(\boldsymbol{x}), \phi_1(\boldsymbol{x}), \cdots, \phi_{m-1}(\boldsymbol{x}) \}$とします。この$\phi(x)$のことを基底関数と呼びます。前回のSVMでは線形分離が扱えたので、基底関数は$$\phi(x)=x$$と等価でした。その他、よく使われる基底関数としては、多項式$$\phi(x)=x^n$$や、ガウス基底$$\phi(x)=\exp\left \{-\frac{(x-\mu)^2}{2\sigma^2}\right \}$$があります。
基底関数を適用することによって、ラグランジュ関数の$x_n^Tx_m$の部分が$\phi(x)_n^T\phi(x)_m$に変わります。
L(\lambda)=\sum_{n=1}^{N}\lambda_n-\frac{1}{2}\sum_{n=1}^{N}\sum_{m=1}^{N}\lambda_n\lambda_mt_nt_m\phi(x)_n^T\phi(x)_m
この$\phi(x)_n^T\phi(x)_m$は、内積計算であり、データ点が多いと計算量が膨大になることから、少し工夫をします。
カーネル関数とカーネルトリック
実は、$\phi(x)_n^T\phi(x)_m$は$k(x_n,k_m)$に置き換えることが可能です。$k(x_n,k_m)$のことをカーネル関数と言います。このように置き換えることで、面倒な内積計算を省略することができます。このことをカーネルトリックと言います。詳細は「カーネルトリック」を参照ください。
特に、上で挙げたガウス基底関数を用いたカーネル関数のことを**RBFカーネル(Radial basis function kernel)**と言ったりします。
最終的にラグランジュ関数は
L(\lambda)=\sum_{n=1}^{N}\lambda_n-\frac{1}{2}\sum_{n=1}^{N}\sum_{m=1}^{N}\lambda_n\lambda_mt_nt_mk(x_n,x_m) \\
\text{subject.to }\sum_{i=1}^n\lambda_it_n=0,0 \leq \lambda_i \leq C
となります。実際にはこの数式を解き、$\lambda$を求めた後に$\boldsymbol{w}$や$w_0$を求めます。
pythonでやってみる
前回は単純なsklearn.svm.LinearSVCで分類を行いましたが、より一般的なsklearn.svm.SVCを使ってみます。
APIドキュメントを見る
APIの説明を見ると以下のようになっています。
class sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)
ここまでの内容を理解しているとだんだんこの説明が理解できるようになってくる。kernelパラメータが基底関数を決めるパラメータで、線形だとlinearで、ガウスカーネルだとrbfになります。ここで重要なのはCとgammaです。
Cは制約条件の強さを決めるパラメータで、大きくなるほど制約が厳しくなります。gammaは、ガウス基底関数の広がりを決めるパラメータで、逆数になっているので、小さいほどなだらかになります。
実装してみる
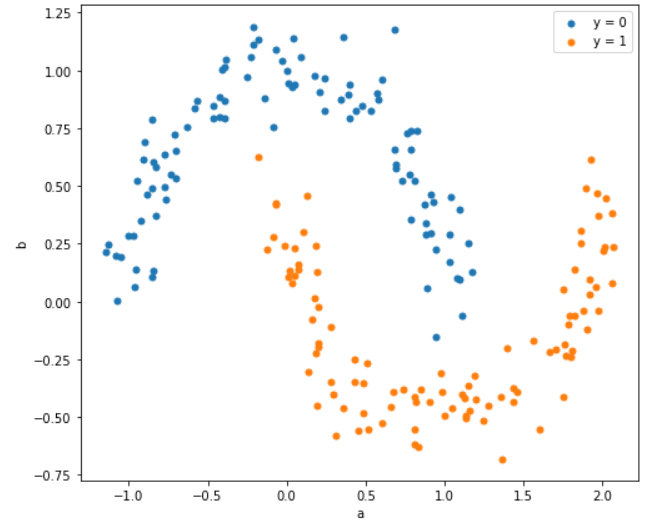
分類するデータは最初に示したデータを使います。実はこのデータは、sklearn.datasets.make_moonsというAPIを使っています。サンプル数やノイズの強弱を指定できます。
ついでに決定境界も図示します。決定境界は線形でないため、等高線として描きます。具体的にはmatplotlibのcontourfという関数を使います。
import numpy as np
import pandas as pd
from sklearn import svm
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
%matplotlib inline
X, y = make_moons(n_samples=200,
shuffle = True,
noise = 0.1,
random_state = 2020,)
a0, b0 = X[y==0,0], X[y==0,1]
a1, b1 = X[y==1,0], X[y==1,1]
model = svm.SVC(C=1.0, kernel='rbf', gamma=1)
model.fit(X, y)
x1_min,x1_max = X[:,0].min() - 0.1,X[:,0].max() + 0.1
x2_min,x2_max = X[:,1].min() - 0.1,X[:,1].max() + 0.1
xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,0.02),
np.arange(x2_min,x2_max,0.02))
Z = model.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.figure(figsize=(8, 7))
plt.contourf(xx1,xx2,Z,alpha = 0.4)
plt.xlim(xx1.min(),xx1.max())
plt.ylim(xx2.min(),xx2.max())
plt.scatter(a0, b0, marker='o', s=25, label="y = 0")
plt.scatter(a1, b1, marker='o', s=25, label="y = 1")
plt.legend()
plt.xlabel("x1")
plt.ylabel("x2")
plt.show()

分離できているみたいですね。APIでは、サポートベクターも取得できるんですが、実際のデータ数と比較しても少ないデータで近似できており、メモリの節約と計算の高速化に寄与しています。
ハイパーパラメータの調整
上ではCとgammaを適当に決めましたが、これを変化させるとどうなるでしょう。実際に描いてみましょう。
list_C = [0.1, 1, 20]
list_gamma = [0.05, 0.5, 20]
x1_min,x1_max = X[:,0].min() - 0.1,X[:,0].max() + 0.1
x2_min,x2_max = X[:,1].min() - 0.1,X[:,1].max() + 0.1
xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,0.02),
np.arange(x2_min,x2_max,0.02))
plt.figure(figsize=(11, 11))
plt.xlim(xx1.min(),xx1.max())
plt.ylim(xx2.min(),xx2.max())
plt.xlabel("x1")
plt.ylabel("x2")
for i in range(len(list_C)):
for j in range(len(list_gamma)):
model = svm.SVC(C=list_C[i], kernel='rbf', gamma=list_gamma[j])
model.fit(X, y)
Z = model.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
ax = plt.subplot(len(list_C), len(list_gamma), i*len(list_C)+j+1)
ax.set_title("C={}, gamma={}".format(list_C[i], list_gamma[j]))
ax.contourf(xx1,xx2,Z,alpha = 0.4)
ax.scatter(a0, b0, marker='o', s=25, label="y = 0")
ax.scatter(a1, b1, marker='o', s=25, label="y = 1")
plt.show()
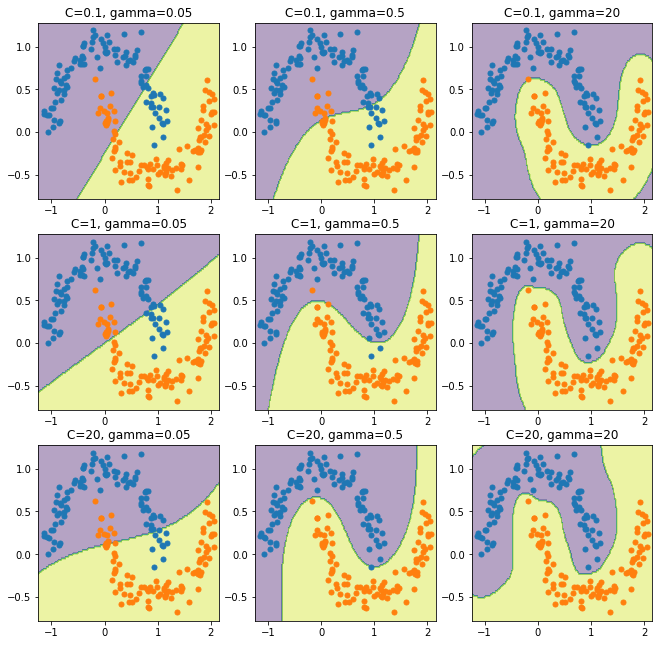
結果は以下のようになりました。
上で説明したように、Cが大きいほどよく分離されており、gammaが大きいほど曲線が複雑になっています。ただ、一番右下になると過学習しているようにも見え、パラメータのチューニングが必要になりそうです。
パラメータをチューニングするためには、サンプルを学習データと検証データに分けて検証データで予測した時の一致度が高くなるパラメータを探すという作業が必要になります。これは**交差検証(Cross Validation)**というのですが、別の機会にまとめてみるつもりです。
まとめ
サポートベクターマシンをハードマージンからソフトマージンに拡張し、非線形分離まで扱えるようにしました。こうして見てみると、かなり複雑なクラス分類もやって退けられるような気がしてきました。ニューラルネットワーク以前に人気だったのも納得ですね。