深層学習後半レポート

※日本ディープラーニング協会のDeep Learning資格試験（E資格）受験に必要な、協会認定の講座プログラム( https://ai999.careers/rabbit/ )がある。
※本プログラム受講に際し、レポート作成はWebやBlogなどで作成する必要があるとのことで、Qiitaで作成することとした。
※個人的なレポート作成用です。

深層学習後半については、時系列データに対する再帰型ニューラルネットワーク、LSTM、GRU、双方向RNN、Seq2Seq、Word2Vec、Attention Mechanism、強化学習、AlphaGo、軽量化・高速化技術、応用モデル、Transformer、物体検知・セグメンテーションの各項目についてそれぞれ100文字以上で要点をまとめるのに加え、Attention Mechanismまでの実装演習結果キャプチャーまたはサマリーと考察、確認テストなど自身の考察結果が必要。

#再帰型ニューラルネットワーク

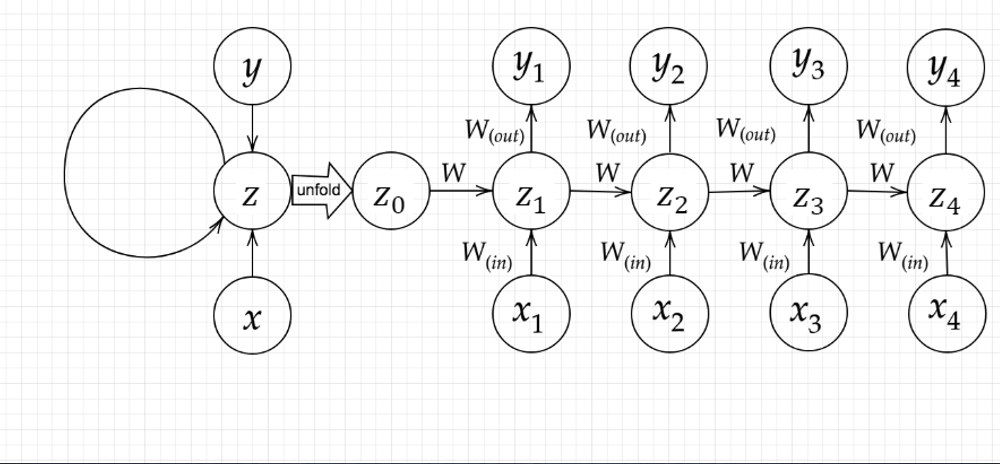
文章や音声の認識や機械翻訳など時系列データに対しては再帰型ニューラルネットワーク(RNN)が用いられる。数学モデルは下図にあるように、入力から中間層をつなぐ重み$W_{(in)}$, 中間層から出力層をつなぐ重み$W_{(out)}$に加え、時間的に1ステップ前と後の中間層をつなぐ重み$W$で表現される。過去の入力が将来の出力にも影響を及ぼすモデルとなっている。

数学的には入力側から

u^t=W_{in}x^{t}+W z^{t-1}+b\\
z^{t}=f(u^t)\\
v^{t}=W_{out}z^t+c\\
y^{t}=g(v^t)\\

で表される。ただし、$f(u^t), g(v^t)$は活性化関数、$b, c$はバイアスである。$u^t$の式が過去入力データと現入力データをつないでいる。最適化の対象となるパラメータ$W_{in}, W_{out}, W, b, c$は、誤差逆伝播法によって勾配を求めてアップデートさせる。時間的に逆方向へ勾配計算をしていくことからBPTT(Backpropagation through time)とも呼ばれている。

\frac{\partial E}{\partial W_{out}}=\frac{\partial E}{\partial v^t}\frac{\partial v^t}{\partial W_{out}}=\delta^{out,t}z^t\\

\frac{\partial E}{\partial c}=\frac{\partial E}{\partial v^t}\frac{\partial v^t}{\partial c}=\delta^{out,t}\\

\frac{\partial E}{\partial W_{in}}=\frac{\partial E}{\partial u^t}\frac{\partial u^t}{\partial W_{in}}=\delta^{t}x^t\\

\frac{\partial E}{\partial b}=\frac{\partial E}{\partial u^t}\frac{\partial u^t}{\partial b}=\delta^{t}\\

\frac{\partial E}{\partial W}=\frac{\partial E}{\partial u^t}\frac{\partial u^t}{\partial W}=\delta^{t}z^{t-1}\\

各パラメータの更新は勾配法の場合以下のようになる。

W^{t+1}_{(in)}=W^{t}{(in)}-\epsilon\frac{\partial E}{\partial W_{(in)}}=W^{t}_{(in)}-\epsilon\sum^{T_t}_{z=0}\delta^{t-z}[x^{t-z}]^T\\

W^{t+1}_{(out)}=W^{t}{(out)}-\epsilon\frac{\partial E}{\partial W_{(out)}}=W^{t}_{(in)}-\epsilon\ \delta^{out,t}[z^{t}]^T\\

W^{t+1}=W^{t}-\epsilon\frac{\partial E}{\partial W}=W^{t}-\epsilon\sum^{T_t}_{z=0}\delta^{t-z}[x^{t-z-1}]^T\\

b^{t+1)}=b^{t}-\epsilon\frac{\partial E}{\partial b}=b^t-\epsilon\sum^{T_t}_{z=0}\delta^{t-z}\\

c^{t+1}=c^t-\epsilon\frac{\partial E}{\partial c}=c^t-\epsilon\delta^{out,t}\\

$W_{(in)}, W, b$はすべての中間層z（出力y）に影響を及ぼすため$\sum ...$　の項が含まれるが、$W_{(out)}, c$は各出力と各中間層の関係を表すパラメータであり$\sum...$の項が含まれない(上図参照)。

以下は、バイナリ足し算を例にしたRNNの実装例。数の足し算を2進数列からRNNによって求めることは実用上は意味がないものの、RNNの感覚（例えば中間層の数を極端に少なくした場合に正解率が非常に悪くなったり多くすると少ないIterationで収束したりなど）をつかむのに役立つ問題である。

import numpy as np
import matplotlib.pyplot as plt

# シグモイド関数とその導関数
def sigmoid(x):
    return 1/(1 + np.exp(-x))

def d_sigmoid(x):
    dx = (1.0 - sigmoid(x)) * sigmoid(x)
    return dx

# 平均二乗誤差とその導関数
def mean_squared_error(d, y):
    return np.mean(np.square(d - y)) / 2

def d_mean_squared_error(d, y):
    if type(d) == np.ndarray:
        batch_size = d.shape[0]
        dx = (y - d)/batch_size
    else:
        dx = y - d
    return dx

binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)

input_layer_size = 2
hidden_layer_size = 32
output_layer_size = 1
weight_init_std = 1
learning_rate = 0.1
iters_num = 1000
plot_interval = 100

# ウェイト初期化 (バイアスは省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)

# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)

u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))

delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))

all_losses = []

for i in range(iters_num):
    
    # A, B初期化 (a + b = d)
    a_int = np.random.randint(largest_number/2)
    a_bin = binary[a_int] # binary encoding
    b_int = np.random.randint(largest_number/2)
    b_bin = binary[b_int] # binary encoding
    
    # 正解データ
    d_int = a_int + b_int
    d_bin = binary[d_int]
    
    # 出力バイナリ
    out_bin = np.zeros_like(d_bin)
    
    # 時系列全体の誤差
    all_loss = 0    
    
    # 時系列ループ
    for t in range(binary_dim):
        # 入力値
        X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
        # 時刻tにおける正解データ
        dd = np.array([d_bin[binary_dim - t - 1]])
        
        u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
        z[:,t+1] = sigmoid(u[:,t+1])
        y[:,t] = sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))


        #誤差
        loss = mean_squared_error(dd, y[:,t])    
        delta_out[:,t] = d_mean_squared_error(dd, y[:,t]) * d_sigmoid(y[:,t])              
        all_loss += loss
        out_bin[binary_dim - t - 1] = np.round(y[:,t])
    
    
    for t in range(binary_dim)[::-1]:
        X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)        

        delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * d_sigmoid(u[:,t+1])

        # 勾配更新
        W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
        W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
        W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))
    
    # 勾配適用
    W_in -= learning_rate * W_in_grad
    W_out -= learning_rate * W_out_grad
    W -= learning_rate * W_grad
    
    W_in_grad *= 0
    W_out_grad *= 0
    W_grad *= 0
    

    if(i % plot_interval == 0):
        all_losses.append(all_loss)        
        print("iters:" + str(i))
        print("Loss:" + str(all_loss))
        print("Pred:" + str(out_bin))
        print("True:" + str(d_bin))
        out_int = 0
        for index,x in enumerate(reversed(out_bin)):
            out_int += x * pow(2, index)
        print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
        print("------------")

lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()

###LSTM (Long Short Term Memory)

一般的なRNNでは長期系列の使用において勾配消失（爆発）が起こりやすくなるため、長期系列の学習が難しいとされていた。そこで、LSTMでは中間層にて長期に依存の学習を有効に行うLSTMブロックを用いた手法が開発された。

勾配消失や勾配爆発の解決法として、勾配を1とする手法CEC（Constant Error Carousel）は、時間依存度に関係なく重みが一律となってしまいメリハリ（どの時間の入力に対する重みがどの時間の出力に影響を与えるかなど）のない学習となってしまう。そこで、入力・出力ゲートに必要な誤差信号が適切に伝搬するようなゲートや不要な情報を忘れる忘却ゲートを活用した手法として開発された。

以下参照
https://qiita.com/KojiOhki/items/89cd7b69a8a6239d67ca

###GRU　(Gated Recurrent Unit)

LSTMの入力ゲートと忘却ゲートを統合した更新ゲートを活用した手法。長期系列の特徴を維持しやすい特性を保ち、LSTMより入出力パラメータを減らしシンプルにした手法である。各時間ステップ間を迂回するショートカットパスが効率的に生成される。

###双方向RNN

一般的なRNNは過去の情報を入力として現在の情報などを出力するが、双方向RNNでは過去の情報だけでなく未来の情報を入力に用いた手法である。未来の情報が入力として使用できる機械翻訳や文章の遂行などのタスクに用いられる。

#自然言語処理
###Seq2Seq

Encoder-Decoderモデルの1種であり、翻訳などにおいては入力の時系列文章（例えば日本語で「おなかが痛いです」）をエンコードし、Decoderではエンコードされた情報をもとに目的とする時系列文章（例えば英語でI have a stomach ache)を出力する。これらのEncoder, DecoderにはRNN（LSTMやGRUなど）が用いられる。
Encoderでは文章が固定長のベクトルに変換される。

なお、会話問題の観点ではSeq2Seqは1問1問しかできない。対してHRED（Hierarchical Recurrent Encoder-Decoder)ではEncoderがまとめた文章全体を表すContext RNNを用いて過去の発言を加味した返答ができるような手法である。

HREDは短く情報に乏しい返答をしがちであるが、VHRED（Latent Variable Hierarchical Recurrent Encoder-Decoder）は確率的なノイズを与えて学習することでより多様な返答が可能な会話モデルとのことである。

以下参照
https://qiita.com/halhorn/items/646d323ac457715866d4
https://arxiv.org/pdf/1605.06069.pdf

また、Auto-Ecoderとは入力と出力を同じにするためのDecoder-Encoderモデルで次元削減に用いられるが、VHREDにおいては、AEに確率的なノイズを与えてAuto-Encoderを活用したVAE（Variational AutoEncoder）が用いられているとのことである。

###word2vec

単語のOne-hotベクトルからEmbedding表現と呼ばれる、1つ1つの単語で意味同士が近くなるベクトルを見つける手法。One-hotベクトルは単語の数だけベクトルが必要になり膨大なデータとなってしまうため、小さいベクトルで単語を表現して言語系の計算をする。
Skit-gram、CBOWと呼ばれるモデルがあり前者は一つの単語から複数の単語を推測し、後者は複数の単語から一つの単語を推測する。以下参照。

###Attention Mechanism

文章など時系列データの中身の注目度合の強さに応じて重みをつける手法。2つのデータの時系列データ間の対応関連を学習する。ベクトルの内積からベクトル（単語）間の類似度が算出され、その類似度を用いた重み付ベクトルが出力される。

全結合と比して関連性のある入力情報に基づく出力を行うので、過学習になりづらく、少ないデータから所望の出力を得やすい。言語系のみならず、画像認識などにも応用されている手法とのことである。以下のWebSiteやYoutubeが参考となった。

https://deeplearning.hatenablog.com/entry/transformer
https://www.youtube.com/watch?v=g5DSLeJozdw

#強化学習

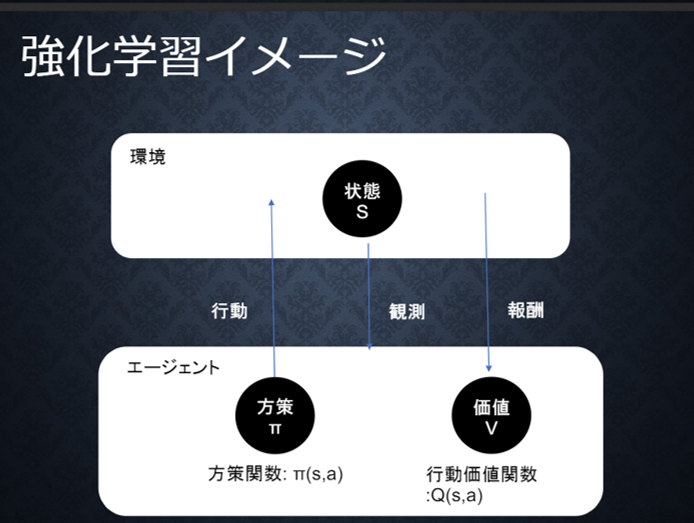
長期的な報酬を最大化できるように、ある環境のなかで最適な行動を選択できる「エージェント」を作ることを目標とする。行動の結果として与えられる利益(報酬)をもとに、行動を決定する原理を改善していく仕組みである。

過去のデータでのみからベストな行動をとる場合は、さらに良い行動をみつけることができないが、これを探索がたりない状態という。一方で、未知の行動のみをとり続けると、過去の知見の利用が足りない状態と考える。

学習においては、上図における方策と価値の学習によって最適化を行っていく。それぞれ、方策関数Π(s,a)と行動価値関数Q(s,a)が用いられる。行動価値関数を、行動する毎に更新することにより学習を進める手法をQ学習という。

方策関数の学習に当たっては、以下のような勾配法を用いてパラメータを最適していく。期待収益を表す式Jを最大とするパラメータを見つける問題であり、更新項が正となっている。方策勾配法と呼ばれている。

\Theta^{(t+1)}=\Theta^{(t)}+\epsilon\nabla J(\Theta)

以下参照

###AlphaGo

畳み込みニューラルネットワークを組み込み強化学習を行った囲碁AIプログラムであり、Alpha Go LeeとAlpha Go Zeroの2種類がある。前者は以下の3ステップより成る。

######1．教師あり学習によるRollout Policy とPolicy Netの学習
畳み込みニューラルネットワーク(CNN)によって次の一手を決定する。プロ棋士の棋譜よりデータを取得し、それを学習させる。ある盤面の基で選んだ一手に関する対数尤度の最大化を行う。

######2．強化学習によるPolicy Netの学習
現状のPolicyNet（方策）とPolicyPoolからランダムに選択されたPolicyNetと対局シミュレーションを行い、自己対戦の強化学習アルゴリズムである。なお、PolicyPoolとは、PolicyNetの強化学習の過程を500Iteraionごとに記録し保存しておいたもの。PolicyPoolからランダムに選択されたものとの対局は、過学習抑制に効果がある。

######3．強化学習によるValue Netの学習
　　ある盤面から「勝てる確率」を算出する評価関数で、強化学習によるポリシーネットワークより、コンピュータ同士の自己対局を繰り返し、ある盤面から始めた時の勝率を自己対局の勝率により決定する。

実践においては、相手の手を読む際に、モンテカルロ木検索という方法が用いられ差し手が決定される。

なお、Alpha Go Zeroは教師あり学習を行わず、強化学習のみで作成される。Policy NetとValue Netを1つのネットワークに統合し、Residual Netと呼ばれるショートカット構造が追加された。

#軽量化・高速化技術

深層学習ではより多くのデータ、パラメータ調整が行われるようになり、高速計算が求められている。そこで、軽量化や高速化のためのいくつかの手法が活用されている。

・データ並列化
データを分割し、それぞれのデータを入力として子モデルをアップデートする勾配を求める。同期型ではこの勾配を平均し、親モデルを更新する。非同期型では、それぞれの子モデルを更新をお互いの計算を待たずに行っていき、学習の終了した子モデルをパラメータサーバにPushする。これが新たな子モデルの学習の入力として用いられる。

・モデル並列化
モデルが大きいときは、モデルの並列化を行う。親モデルを各ワーカーに分割し、同じデータからそれぞれのモデルを学習させる。すべてのデータで学習が終わった後で、1つのモデルを復元。

・GPU
CPUが高性能なコアが少数、複雑連続的な処理が得意なのに対し、GPUは比較的低性能なコアが多数あり、簡単な並列計算が得意である。深層学習では単純な行列計算が多いので高速化が可能。

・モデル軽量化
モデルの精度を維持しつつパラメータや演算回数を提言する手法。

・量子化
64bit浮動小数点を32bitやそれ以下の精度に落とすことでメモリと演算処理の削減を行う。bitを落としすぎると精度が落ちるが、16bit程度でも十分な精度を保つ場合が多い。

・蒸留
複雑なモデルの教師モデルと、軽量モデルである生徒モデルを用いて、教師モデルと生徒モデルの出力誤差を使い重みを更新することで軽量モデルを作成する。

・プルーニング
寄与の少ないニューロンの削減を行い、モデルの圧縮を行うことで高速化計算を行う手法。

#応用モデル

通常の畳み込みレイヤーでは入力データが$H\times W\times C$（縦のグリッド数、横のグリッド数、チャネル数）, カーネルサイズ$K\times K\times C$,
出力チャネル数（フィルタ数）$M$とすると、ストライド1でパディング無の場合の畳み込み計算は$H\times W\times K\times K\times C\times M$、出力マップは$H\times W\times M$である。

MobileNetsはDepthwise ConvolutionとPointwise Convolutionの組み合わせで軽量化をおこなった手法を採用している。

Depthwise Convolutionでは、カーネルは$K\times K$の1つ（同じもの）を各チャンネルに適用し、出力マップの計算$H\times W\times C\times K\times K$, 出力マップは$K\times K\times C$となる。また、Pointwise Convolutionでは、$1\times 1\times C$のフィルタをM個作成して、計算量$H\times W\times C\times M$で出力マップ$H\times W\times M$を得る。これらを組み合わせることで、通常の畳み込みと比して計算量の削減が可能である。

また、ResNetはショートカット結合が特徴的なモデル、DenseNetでは前方の各層からの出力を後方の層への入力として用い、また、特徴マップをチャネル方向に結合する特徴がある。WaveNetは時系列データに対する畳み込みを行い、Dilated Convolutionと呼ばれる、層が深くなるにつれて畳み込むリンクを切り離す手法（受容野を増やす手法）。

#Transformer

RNNを用いず、Attensionのみで時系列データを扱う。以下で表されるスケール・ドットアテンション機構と呼ばれる手法が用いられている。

Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}}) V

ただし、Qはクエリ、Kはキー、Vはバリューを意味する。$d_k$はQ, Kの次元で、勾配が小さくならないように$\sqrt{d_k}$の除算が含まれる。質問文（Q）を入力すると、参照すべき場所（K）がきまり、その場所の回答の候補（V）が得られる。

Transformerでは、このスケールドットアテンション機構が並列に並べられたマルチヘッドアテンションがエンコーダ、デコーダー側双方で用いられている。QとKが同じデータに由来するので、このAttentionをSelf Attentionと呼ぶ。ある文章の単語とそれぞれの単語との関係性が考慮される。代名詞がさす名詞はどれかを確率的に予測するイメージ。デコーダー側では、予測すべき単語を予測時に使用しないよう、マスクが掛けられている。また、系列の順序に関する情報は、ポジショニングエンコーディングというベクトルによって考慮されている。

また、BERT(Bidirectional Encoder Representation from Transformers)は、Transformerのエンコーダを用いて過去の単語も将来の単語も使って対象の単語を予測する手法。

#物体検知・セグメンテーション

物体検知には１．写真に何が示されているか分類出力する問題、２．Bounding Boxを用いた物体検知、３．各ピクセルに対して単一のクラスラベルを用いた意味領域分割（Semantic Segmentation）、４．個別領域分割（Instance Segmentation）に主に分類され、１から４に向かってより難易度の高い問題である。

２．Bounding Boxを用いた物体検知の場合、どの長方形に、何が、どの程度のConfidenceで存在しているか、についてが出力される。

物体検知に当たっては、精度評価のためのデータセット（物体検知に関して正解のある写真などのデータ）が広く用いられてきた。代表的なデータセットとしては、VOC12、ILVRC17、MS COCO18、OICOD18があり、以下の特徴がある。目的に応じたデータセット選択が必要である。

・VOC12（Visual Object Classes）
クラス数が20、TrainとValidation加えて11,540のデータがあり、ひと画像あたりのBox数は2.4。Instance Annotationがある。

・ILSVRC17（ImageNet Scale Visual Recognition Challenge）
クラス数200、TrainとValidation加えて476,668のデータがある。ImageNet（21,841クラス、1400万枚）の一部。Box/画像は1.1と、1画像あたり1つの物体しか映っていないようなデータ。Instance Annotationは無し。

・MS COCO18（Microsoft Common Object in Context）
クラス数80、TrainとValidation合わせて123,287のデータがある。Box/画像は7.3と、一枚の画像に7枚とかの物体が移ったデータとなっている。Instance Annotationある。

・OICOD18（Open Images Challenge Object Detection）
クラス数500、TrainとValidationデータ1,743,042のデータがある。Open Images V4の一部。Box/画像は7.0。Instance Annotationあり。

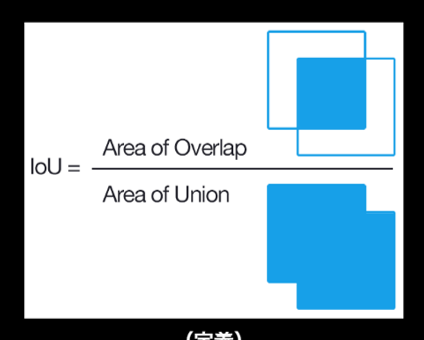
物体検知の評価においては、0～1の間のConfidence、閾値以上の値のものを正として、その物体のBounding Boxの精度がIoU（Intersection over Union）という指標によって評価される。

また、IoU閾値固定、Confidence閾値変えた場合のPrecisionをRecallの関数とするPR曲線の面積であるAP（Average Precision）、あるいは各クラスのAP平均mAP(mean Average Precision)も、画像検知の指標としてよく使われる。MS COCOでは、IoUの閾値も変化させ、位置の決定精度をより厳しくした指標mAPcocoが導入された。

検出速度においては、Frams Per Second(FPS)や、inference timeなどが用いられている。

物体検知のフレームワークにおいては、候補領域の検出とクラス推定を別々に行う2段階検出器（RCNNなど）と、これらを同時に行う1段階検出器（SSD、Single Shot DetectorやYOLOなど）がある。1段階検出は相対的に精度が低いが計算量が小さく推論も早い傾向がある。SSDでは、CNN等で得られる複数解像度の特徴マップから、Default Boxを数千用意して、大小の様々な物体検知への対応を行っている。誤差関数においては、Confidenceと検出位置のそれぞれの損失関数を組み込んだものが用いられている。

Semantic Segmentationは、通常の深層CNNを用いると、多層化に伴い解像度が小さくなっているため、ピクセル毎の意味分割のためにはDeconvolutionなどを用いたUp-samplingが必要となる（ここでいうDeconvolutionは、Convolutionが現画像*フィルタ→特徴量画像に対して、特徴量/フィルタ’→現画像といった逆畳み込みの意味ではないとのことである）。全結合層を用いないFully Convolutional Network(FCN)を用い、各Pooling段階での情報を伝達して出力がなされる。