2021/6/14 - 自作関数更新
MATLAB Student Ambassadorとして活動するにあたり, Twitterでのアイコンで使うロゴマークを考える必要があった. そこで, 当時勉強していた数理最適化手法である拡張ラグランジュ法を用いたロゴを作成した. 本記事はその履歴である.
拡張ラグランジュ関数法とは
拡張ラグランジュ関数法は, 条件付き非線形最適化問題を解く手法の1つです.
ここでは, 以下のような問題を考えていきます.
最小化 $f(x)$
条件 $g(x) = 0$
これが意味しているのは,
「$g(x)=0$上の点で, $f(x)$が最小になる点を探したい!!」
です.
実は条件の無い非線形最適化問題では, ニュートン法などのシンプルで強力な手法が考案されていますが, 条件がついてしまうとニュートン法の適用が難しくなります.
なので, 昔の偉人たちは, 「どうにかして条件付最適化問題を条件なし最適化問題にしたい」と考えました.
その結果, 生み出された考えが, ペナルティ関数を使うことにより,
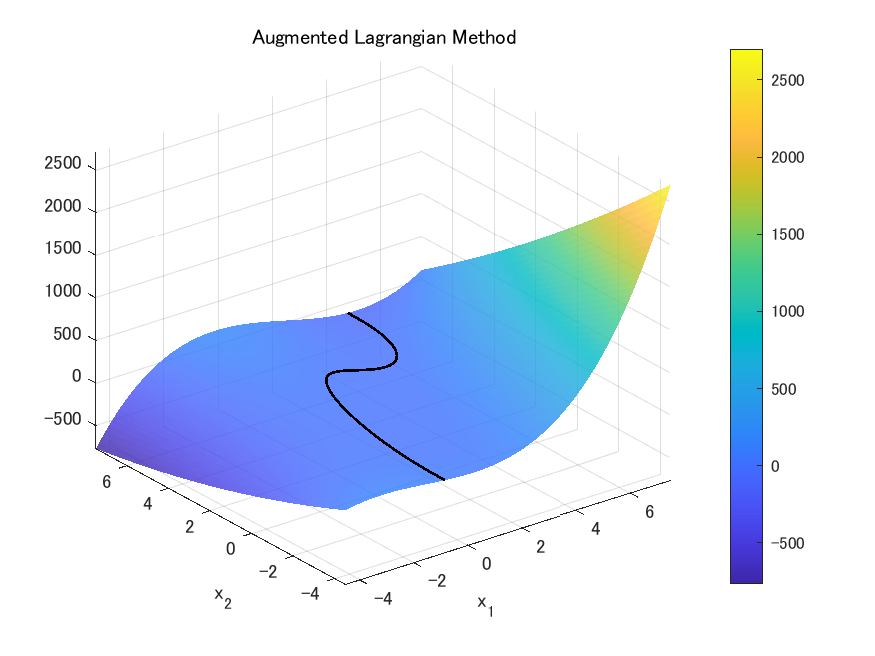
図のような最小化したい目的関数$f(x)$を
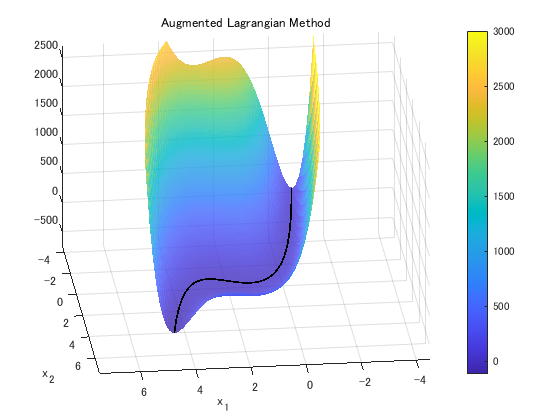
このように峡谷のような形にすれば, ニュートン法で条件を満たす解に向かって最適化できるし, これにラグランジュ乗数法を使えばもっと強力になるのではないか... というものでした.
図のような峡谷状の目的関数を数式にすると, 拡張ラグランジュ関数
$$ L_{\rho}(x,u)=f(x)+\sum_{i=1}^{m}u_ig_i(x)+\frac{\rho}{2}\sum^{m}_{i=1}g_i(x)^2 $$
が得られます. この関数を最小化することで最適解を見つけるのが拡張ラグランジュ関数法です.
詳しい解き方や立式については, 以下の本を参考にさせていただきました.
梅谷俊治, しっかり学ぶ数理最適化 モデルからアルゴリズムまで, 講談社, 2020
実際にMATLABでやってみた!!
今回やってみた問題は,
最小化 $f(x_1,x_2) = 4x_1^3-4x_1^2x_2+3x_2^2-8x_1$
条件 $g(x_1,x_2) = \frac{1}{3}x_1^3-\frac{9}{4}x_1^2+\frac{9}{2}x_1+1-x_2 = 0$
です. (特別な意味はなし..)
実行環境はMATLAB 2021aとなっています.
初期状態の決定
まず, 初期状態を決定していきます.
x0 = [-2;-2]; % Initial Point x0
u0 = 0; % Initial Lagrange Multiplier
rho0 = 1; % Initial Penalty Parameter
今回は, $(x_1,x_2) = (-2,-2)$を初期点として, 開始しています.
関数の指定
ここから, 解くべき問題の目的関数と条件を入力していきます. 計算には, 各関数の偏微分も必要になってくるので, それらも以下に書きます.
まずは, 目的関数$f(x)$
f = @(x) 4*x(1,:).^3-4*x(1,:).^2.*x(2,:)+3*x(2,:).^2-8*x(1,:); % Target Function
df = @(x) [8*x(1,:)-4*x(2,:)-8;-4*x(1,:)+6*x(2,:)]; % Partial Differential of Target Function
次に, 条件$g(x)$
g = @(x) x(1,:).^3./3-9/4*x(1,:).^2+9/2*x(1,:)+1-x(2,:); % Constraint Function
dg = @(x) [x(1,:).^2-9/2*x(1,:)+9/2,-1]; % Partial Differential of
最後に, ペナルティ関数の増やし方のルールを
nrho = @(rho) 2*rho;
と指定します.
拡張ラグランジュ関数法の利用
今回は自作で用意した関数を用いて, 最適解を求めていきます. (自作関数は末尾に記載)
[x,u] = augLag(df,g,dg,nrho,x0,u0,rho0);
-- Start --
Position x
-2
-2
f(x) = 28.000000
df(x) = -16.000000
df(x) = -4.000000
g(x) = -17.666667
Iteration Step: 11
-- Finish --
Position x
2.8461
3.2666
f(x) = -4.381479
df(x) = 1.702261
df(x) = 8.215097
g(x) = 0.000000
結果の可視化
ここから結果を可視化します.
% Visualize Range
min1 = -3;
min2 = -3;
max1 = 5;
max2 = 5;
% Create Surface and constraints
x1 = min1:(max1-min1)/99:max1;
x2 = min2:(max2-min2)/99:max2;
tf = zeros(length(x2),length(x1));
for i=1:length(x1)
for j=1:length(x2)
tf(j,i) = f([x1(i);x2(j)]);
end
end
cx2 = g([x1;zeros(1,length(x1))]);
cz = f([x1;cx2]);
% Visualize
figure;
rotate3d on
surf(x1,x2,tf,'EdgeColor','none','FaceAlpha',0.8);
hold on
plot3(x1,cx2,cz,'k-','LineWidth',1.3);
plot3(x(1,:),x(2,:),f(x),'-r.','MarkerSize',12);
plot3(x(1,end),x(2,end),f(x(:,end)),'g.','MarkerSize',25);
hold off
colorbar
grid on
title('Augmented Lagrangian Method');
xlabel('x_1');
ylabel('x_2');
str = sprintf('Solution (%e,%e)',x(1,end),x(2,end));
legend('Target Function','Constraints','Augmented Lagrangian Method',str,'Location','southoutside');
xlim([min1 max1]);
ylim([min2 max2]);
zlim([min(min(tf)) max(max(tf))]);
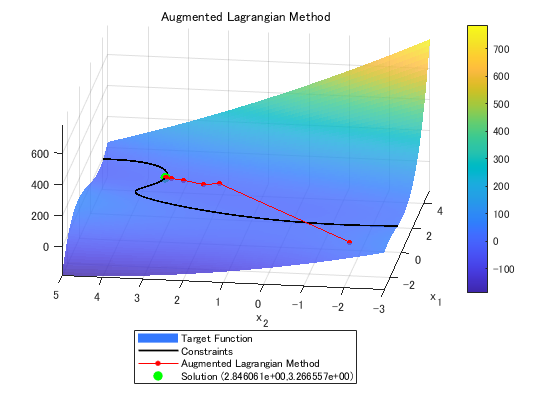
view(3);
このように, 初期点からだんだんと移動して, 最適解を見つけ出すことができました.
付録
自作関数はこちら (今回対象とした問題以外での検証等は行っておりません)
function [x,u] = augLag(f,df,g,dg,nrho,x0,u0,rho,e,n)
%
% augLag - Augmented Lagrange Method
%
% [x,u] = augLag(f_func,df_func,g_func,dg_func,pnlty_func,x0,u0,rho0)
%
% -Inputs-
% x0 - Initial Point
% u0 - Initial Lagrange Multiplier (Unspecified - 0)
% rho0 - Initial Penalty Parameter (Unspecified - 1)
% f_func - Target Function
% df_func - Partial Differential of Target Function
% g_func - Constraint Function
% dg_func - Partial Differential of Constraint Function
% nrho_func - Rule to determine next penalty parameter (Unspecified - 2*rho)
% e - Allowable Error (Unspecified - 10^(-6))
% n - Max Number of Iteration (Unspecified - 1000)
%
% -Outputs-
% x - Solution Process
% u - Lagrange Multiplier Process
%
%
% --- Usage Example ---
%
% x0 = [-2;-2];
% u0 = 0;
% rho0 = 1;
%
% f = @(x) (x(1,:)-2).^4 + (x(1,:)-2*x(2,:)).^2;
% df = @(x) [4*(x(1,:)-2).^3+2*(x(1,:)-2*x(2,:));-4*(x(1,:)-2*x(2,:))];
% g = @(x) x(1,:).^2-x(2,:);
% dg = @(x) [2*x(1,:),-1];
% pnlty = @(rho) 2*rho;
%
% [x,u] = augLag(df,g,dg,pnlty,x0,u0,rho0);
%
% ---------------------
%
%
switch nargin
case 9
e = 10^(-6);
case 8
e = 10^(-6);
n = 1000;
case 7
e = 10^(-6);
n = 1000;
nrho = @(rho) 2*rho;
case 6
e = 10^(-6);
n = 1000;
nrho = @(rho) 2*rho;
rho = 1;
case 5
e = 10^(-6);
n = 1000;
nrho = @(rho) 2*rho;
rho = 1;
u0 = 0;
end
if (nargin < 5)
error('Invalid Inputs');
help augLag
end
judge = 0;
u = [u0];
x = [x0];
i = length(x(1,:));
fprintf('-- Start --\n')
print_prc(f,df,g,x);
% Iteration Start
while (judge == 0)
x(:,i+1) = qNewton(df,g,dg,x(:,i),u(:,i),rho,e,n);
if (sqrt(sum((x(:,i+1)-x(:,i)).^2)) < e)
judge = 1;
else
u(:,i+1) = u(:,i) + rho*g(x(:,i+1));
rho = nrho(rho);
i = i+1;
end
end
if (judge == 0)
error('The calculation cannot converge!!');
else
fprintf('\nIteration Step: %d\n\n',length(x(1,:)));
fprintf('\n-- Finish --\n')
print_prc(f,df,g,x);
end
end
% Quasi-Newton Method
function x = qNewton(df,g,dg,x,u,rho,e,n)
alpha = 0.1;
judge = 0;
i = 1;
B = length(x(:,1));
while (judge == 0 && i < n)
if (sqrt(sum(daug_Lag(df,g,dg,x,u,rho).^2)) < e)
judge = 1;
else
% Update
nx = x - alpha*inv(B)*daug_Lag(df,g,dg,x,u,rho);
% BFGS Equation
s = nx - x;
y = daug_Lag(df,g,dg,nx,u,rho) - daug_Lag(df,g,dg,x,u,rho);
B = B - (B*s*(B*s)')/(s'*B*s)+(y*y')/(s'*y);
x = nx;
i = i+1;
end
end
end
% Differential of Augmented Lagrangian Function
function answ = daug_Lag(df,g,dg,x,u,rho)
answ = df(x) + u*dg(x)' + rho*g(x)*dg(x)';
end
% Print Process
function print_prc(f,df,g,x)
fprintf('Position x\n');
disp(x(:,end));
fprintf('f(x) = %f\n',f(x(:,end)));
fprintf('df(x) = %f\n',df(x(:,end)));
fprintf('g(x) = %f\n\n',g(x(:,end)));
end