logyX<logxY の、座標変換をつかったいい感じの解き方

問題

　以下の不等式を表す領域を座標平面上に図示せよ．

\log_y x < \log_x y

（2016 茨城大）

解法 1

　真数および底の条件より、

• $x>0$ かつ $x \neq 1$ かつ $y>0$ かつ $y \neq 1$

　$\log_y x$ を $t$ とすると、不等式は、

t < \frac{1}{t}

　と表せる。これに、$t^2$（明らかに正）をかける。

\displaylines{
t^3 < t \\
t^3-t < 0 \\
t(t^2-1) < 0 \\
t(t-1)(t+1) < 0 \\
t<-1 , \quad 0<t<1 \\
\log_y x<-1 , \quad 0<\log_y x<1 \\
}

　さらに、$\log$ を外していくが、このとき、底が $1$ であるときを境に不等号が反転することに注意する。

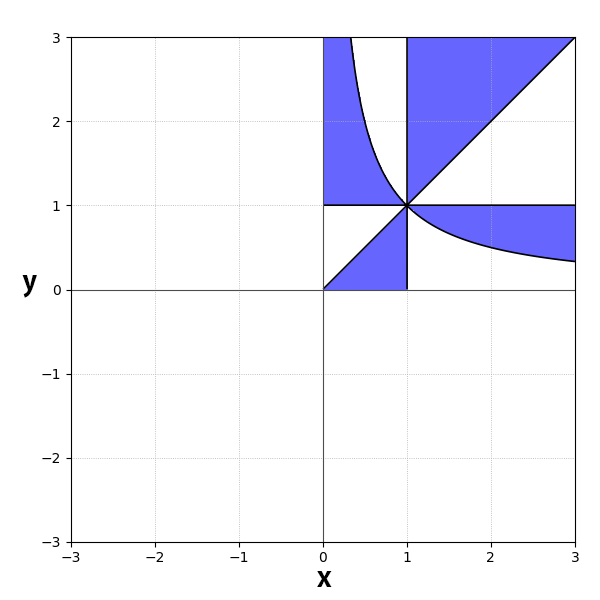
• $0<y<1$ のとき、

\displaylines{
\log_y x<-1 \Leftrightarrow x>\frac{1}{y} \Leftrightarrow y>\frac{1}{x}  \\ 
0<\log_y x<1 \Leftrightarrow 1>x>y
}

• $1<y$ のとき、

\displaylines{
\log_y x<-1 \Leftrightarrow x<\frac{1}{y} \Leftrightarrow y<\frac{1}{x}  \\ 
0<\log_y x<1 \Leftrightarrow 1<x<y
}

　最終的に、以下の図が得られる。

※境界を含まない

ややこしい

　この解法では、かなりややこしい場合分けが必要になります。

　座標変換を利用して、これを場合分けなし（本質的にはあまり変わりませんが）で解いてみます。

解法 2

\displaylines{
p = \ln(x) \\
q = \ln(y)
}

　なる座標系を考える。このとき、与えられた条件は、

\displaylines{
 \log_y x < \log_x y \\
 \frac{\ln{x}}{\ln{y}} < \frac{\ln{y}}{\ln{x}} \\
 \frac{p}{q} < \frac{q}{p}
}

　と整理できる。なお、$x \neq 1$ および $y \neq 1$ から、$p \neq 0$ および $q \neq 0$ は保証される。

　両辺に $p^2q^2$（明らかに正）を乗じて、

\displaylines{
p^3q < pq^3 \\
p^3q-pq^3 < 0 \\
pq(p^2-q^2) < 0 \\
pq(p+q)(p-q) < 0
}

　を得る。
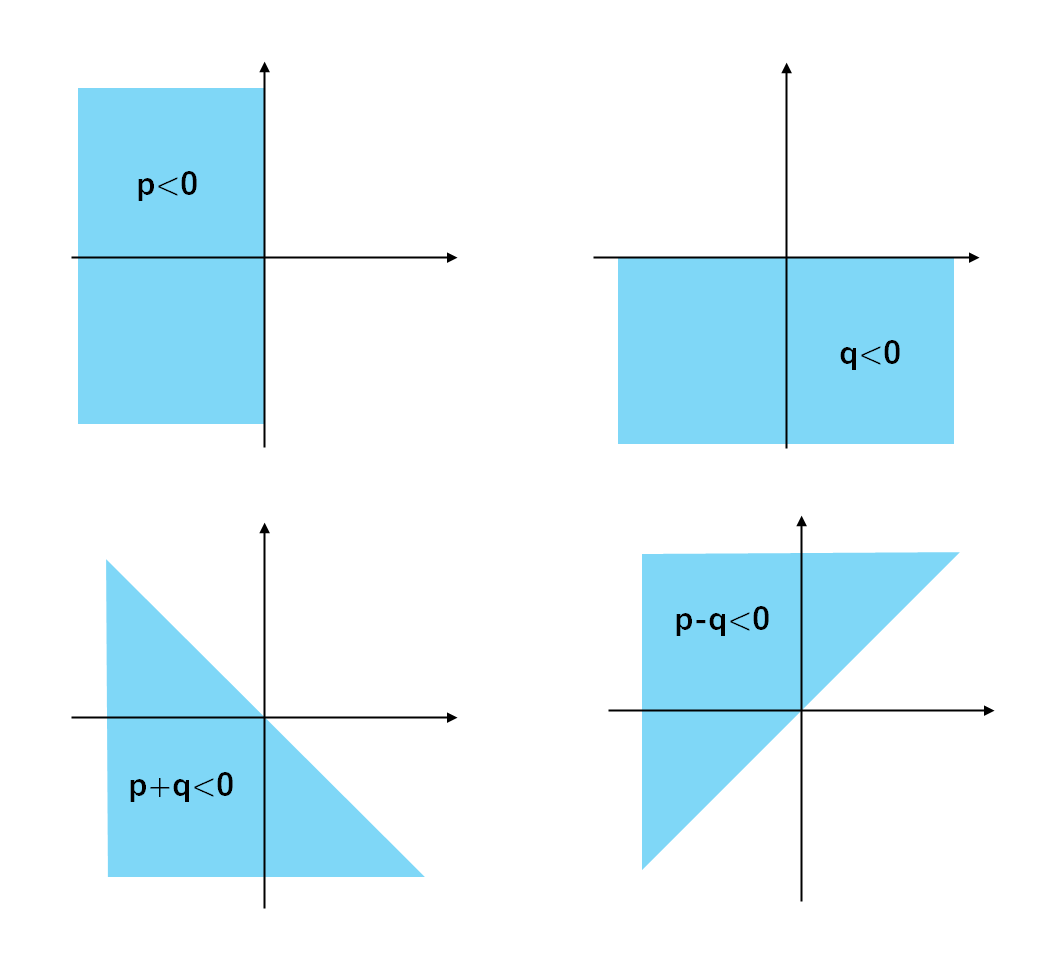
　このとき、左辺の正負は、$p,q,p+q,p-q$ の $4$ つの因数にどれだけ負の数があるかによって決まる。具体的には、負の数が偶数個ならば正、そうでないときは負である。

　各因数を満たす領域は以下のようになる。

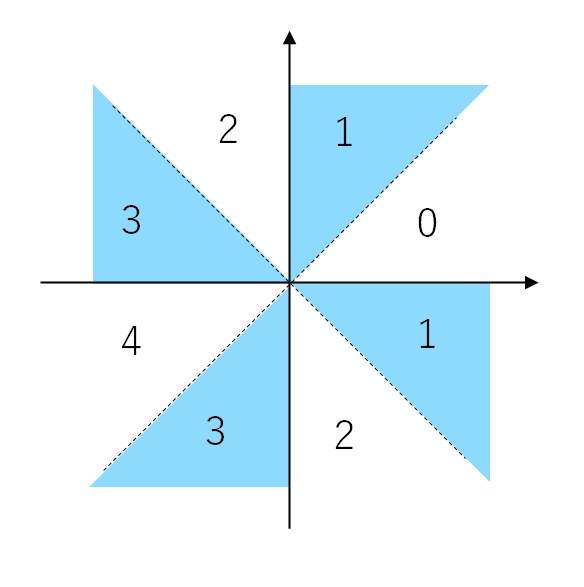
　これらを重ね合わせ、領域が重なる個数をカウントし、奇数個の領域に色をつけた図が以下になる。

　つまり、$pq$ 平面における図は以下である。

※境界を含まない

　さて、$pq$ 平面の座標系を $xy$ 平面の座標系に変換する。

\displaylines{
p = \ln{x} \\
q = \ln{y}
}

　より、

\displaylines{
x = e^p \\
y = e^q
}

　という逆変換がとれる。

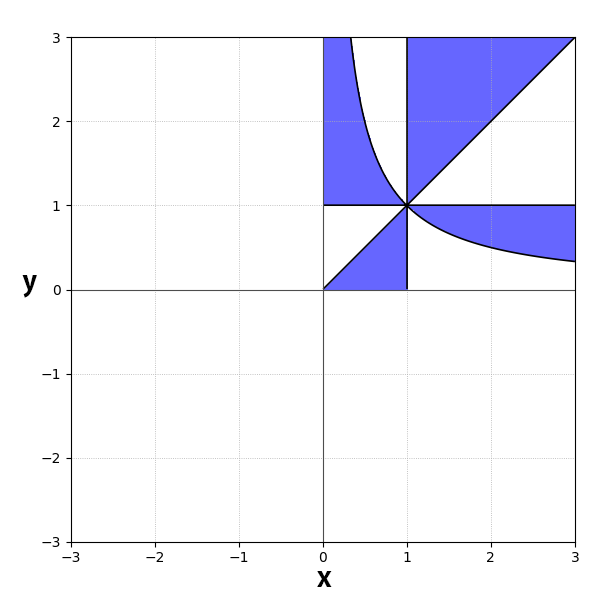
　これは、$p,q\in(-\infty<0) \cup (0<\infty)$ を $x,y \in (0<1)\cup(1<\infty)$ に写す連続写像である。

　また、各直線（広義の曲線）は、

\displaylines{
p=0 \Leftrightarrow x = e^0 = 1 \\
q=0 \Leftrightarrow y = e^0 = 1 \\
p=q \Leftrightarrow e^p = e^q \Leftrightarrow y = x \\
p=-q \Leftrightarrow e^p = e^{-q} \Leftrightarrow y = \frac{1}{x} \\
}

　と変換され、以下の図のようになる。

※境界を含まない

こんな変換、他に何に使うの

　両対数グラフ で使います。

コード描画に使ったプログラム

AI 製ですが、いろいろな陰関数を表示するのに使えそうなので、

import numpy as np
import matplotlib.pyplot as plt

def plot_implicit_region(
    f,                      # ベクトル化可能な関数 f(x, y) -> ndarray
    xlim=(-3, 3),
    ylim=(-3, 3),
    compare: str = "<=",    # "<", "<=", ">", ">="
    domain=None,            # 追加のドメイン制約: g(x,y)->bool配列 を渡す（省略可）
    grid=600,               # 解像度
    cmap="Blues",           # 塗りつぶし用カラーマップ
    alpha=0.6,              # 塗りの透明度
    show_boundary=True,     # f(x,y)=0 の等高線を描く
    boundary_color="k",
    boundary_lw=1.2,
    title=None,
    equal_aspect=True,
):
    """
    例:
      f = lambda x,y: x*y*(x+y)*(y-x)        # f(x,y) < 0 を塗る
      plot_implicit_region(f, xlim=(-3,3), ylim=(-3,3), compare="<")
    """
    x = np.linspace(xlim[0], xlim[1], grid)
    y = np.linspace(ylim[0], ylim[1], grid)
    X, Y = np.meshgrid(x, y, indexing="xy")

    # 数値的不安定を抑える
    with np.errstate(all='ignore'):
        Z = f(X, Y).astype(float)

    # ドメイン制約（例: (X>0)&(Y>0) など）を適用
    mask_domain = np.ones_like(Z, dtype=bool)
    if domain is not None:
        with np.errstate(all='ignore'):
            mask_domain = domain(X, Y)

    # 不等式を判定
    if compare == "<":
        mask_region = Z < 0
    elif compare == "<=":
        mask_region = Z <= 0
    elif compare == ">":
        mask_region = Z > 0
    elif compare == ">=":
        mask_region = Z >= 0
    else:
        raise ValueError("compare は '<', '<=', '>', '>=' のいずれかを指定してください。")

    mask = mask_region & mask_domain

    # 描画
    fig, ax = plt.subplots(figsize=(6, 6))
    # 塗り（True を 1、False を NaN にして imshow）
    region = np.where(mask, 1.0, np.nan)
    ax.imshow(
        region,
        origin="lower",
        extent=[xlim[0], xlim[1], ylim[0], ylim[1]],
        cmap=cmap,
        alpha=alpha,
        interpolation="nearest",
        aspect="auto",
    )

    # 境界 f=0
    if show_boundary:
        # Z に NaN があると等高線が途切れるのでドメイン外だけ NaN に
        Zb = np.where(mask_domain, Z, np.nan)
        try:
            cs = ax.contour(X, Y, Zb, levels=[0.0], colors=boundary_color, linewidths=boundary_lw)
            # ax.clabel(cs, fmt="f(x,y)=0", inline=True, fontsize=8)
        except Exception:
            pass  # 等高線が引けないケースは無視

    # 軸や体裁
    if equal_aspect:
        ax.set_aspect("equal", adjustable="box")
    ax.set_xlim(*xlim)
    ax.set_ylim(*ylim)
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    if title:
        ax.set_title(title)
    ax.grid(True, ls=":", lw=0.6)

    # 原点軸をわかりやすく
    ax.axhline(0, color="0.3", lw=0.8)
    ax.axvline(0, color="0.3", lw=0.8)

    plt.tight_layout()
    plt.show()


# --- 使用例1：最近話題の  xy(y+x)(y-x) < 0  を塗る ---
f1 = lambda x, y: x*y*(x+y)*(x-y)
plot_implicit_region(
    f1, xlim=(-3, 3), ylim=(-3, 3),
    compare="<",
    cmap="brg",
    title="Example 1: p*q*(p+q)*(p-q) < 0"
)

# --- 使用例2： log_x(y) < log_y(x) を塗る（x>0, y>0, x≠1, y≠1 のドメイン）---
def f2(x, y):
    # log_x(y) - log_y(x) < 0  <=>  log(y)/log(x) - log(x)/log(y) < 0
    return np.log(x)/np.log(y) - np.log(y)/np.log(x)

eps = 1e-6
domain2 = lambda x, y: (x > 0) & (y > 0) & (np.abs(x-1) > eps) & (np.abs(y-1) > eps)

plot_implicit_region(
    
    f2, xlim=(-3, 3), ylim=(-3, 3),
    compare="<",
    domain=domain2,
    cmap="brg",
    title="Example 2: log_y(x) < log_x(y) with domain x>0,y>0,x≠1,y≠1"
)