木と列について
以下、「木」はとくに工夫のない素朴な木構造、「列」は一連のポインタに値が設定されているデータ構造とします。
大前提として、
- 木は構造を動的に変更するのが得意で、ランダムアクセスが苦手
- 列はランダムアクセスが得意で、状態を動的に変更するのが苦手
という特性があります。
木が得意な操作
以下のような問題を考えます。
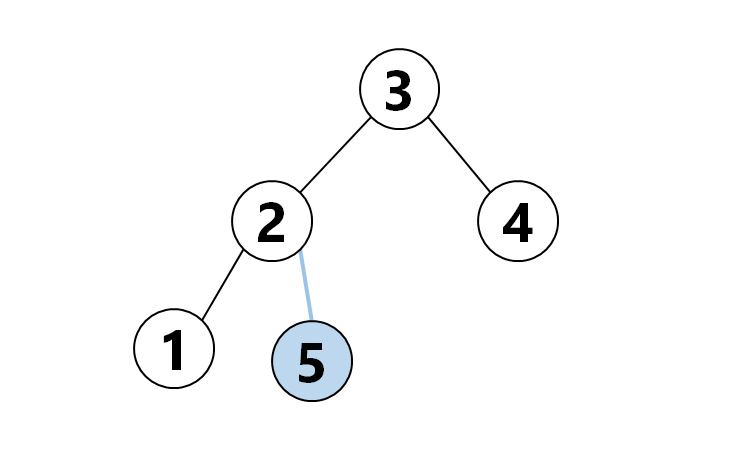
- 配列 $\lbrace1,2,3,4\rbrace$ が与えられる。この配列の $\lbrace 2 \rbrace$ の直後に $\lbrace 5 \rbrace$ を追加せよ
列でこれをやろうとすると大変です。
このように、後続の要素をすべて変更して住所を振り直す必要があります。また、ここでは深掘りしませんが、そもそも「最初にいくつ(一連の)住所を確保すればいいのか」という別の問題もあります。
一方、木ではこのように、ノードに子を追加するだけでこの操作を実現できます。
なお、木から順番を復元するにはまた別の手間がいりますが、例えば「大量に挿入/削除が与えられたあとに $1$ 回復元するだけ」といった設定ならばとくに問題にはなりません。
列が得意な操作
一方で、以下のような問題を考えます。
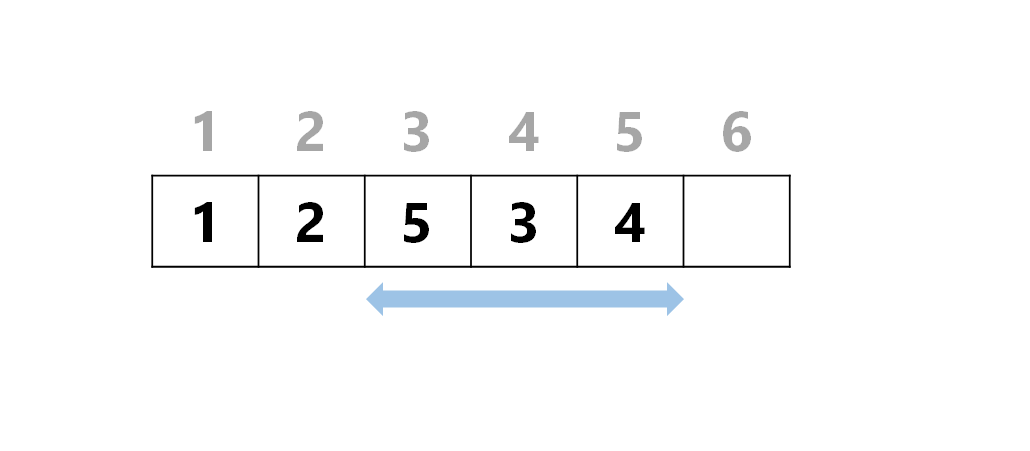
- 配列 $\lbrace 1,2,3,4,5 \rbrace$ の $3$ 番目から $5$ 番目の要素の合計を答えよ
木でこれをやろうとすると大変です。
木の頂点からは、何番目の要素がどこにあるのかは直接はわかりません。
一方、列でこれをするのは簡単です。
更に、複数クエリになっても、累積和を事前計算するなどの対策が可能です。
set の罠
木の弱点のわかりやすい例として、C++ には setの罠 として知られている現象があります。
set.lower_bound(x)lower_bound(set.begin(),set.end(),x)
求められるものは同じですが、下の書き方をするとすごい時間がかかってしまうというものです。具体的には $O(N)$($N$ は要素数)。
この理由は、以下の図を見ていただければ察していただけるかと。
同様の理由で、
distance(set.begin(),itr)
には $O(\log{N})$ ではなく $O(N)$ の計算量がかかります。
トレードオフ
究極的には、木の要素は「自分自身がいまどこにいるのか」がわかりません。わかるのは自分の身の回り(親が誰か、子が誰か)だけです。
一方で、列の要素は「自分自身がいまどこにいるのか」がわかります。これを ランダムアクセス 可能であるといいます。これは、「$1$ 番目の要素には $A_1$ があり、$2$ 番目の要素には $A_2$ があり……」という情報が固定されているからです。しかし、挿入や削除によってこの順序が崩れてしまうと、その再構築に大きなコストがかかります。
順序を崩さない(崩せない)こととランダムアクセス可能であることは不可避的に結びついています。よって、木と列のメリットはトレードオフにあり、両立は一見難しいように見えます。
set の良いところ
しかし、先に挙げた set は部分的にこれを両立しているように見えます。
例えば、set の良いところは自動的にソートされることですが、木構造を考えれば自然なメリットです。
ここで、極端な例として、もし木構造が、
こうなっていたら、$O(N)$ の探索回数を要します。そして、データの追加の順番によってはこうなってもおかしくないです。
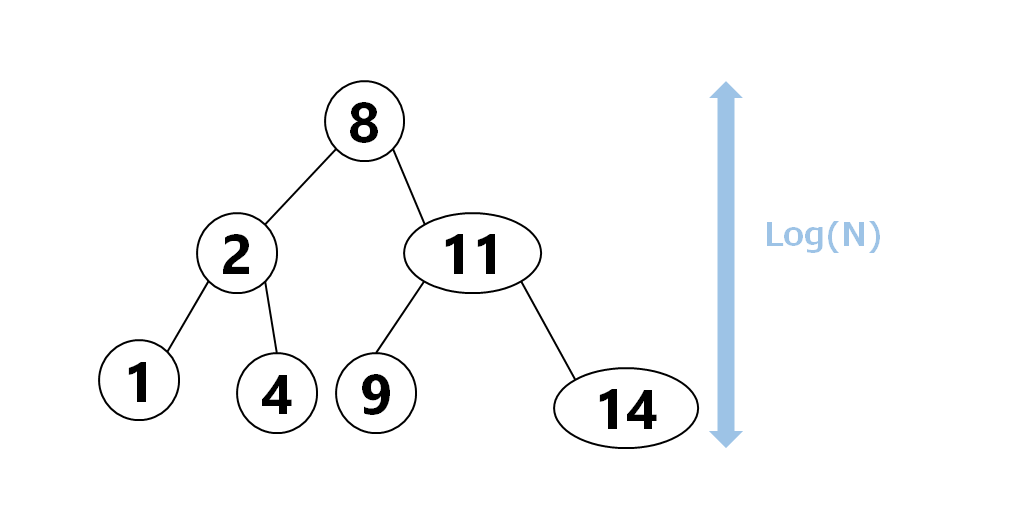
それなのに、なぜ $O(\log{N})$ でできているかというと、set は 平衡二分木だから です。
このように、上手い感じに均等にわかれるようになっています。こうすれば、要素数 $N$ に対して、高さは $O(\log{N})$ に抑えられます
我々が漫然と値を追加している間、set の内部では高さが平衡になるように調整してくれているのです。
という訳で、set が色々なことをバランスよくできるのは、平衡二分木のおかげなのでした。
セグメントツリー
セグメントツリーもまた、本来であればどちらかに最悪 $O(N)$ かかる操作(一点更新と区間取得)を両者 $O(\log{N})$ で済ませることのできる優れたデータ構造です。
これは全要素を葉とするような平衡二分木を構築することによって実現できます。
これによって、どのような一点更新と区間取得をそれぞれ $O(\log{N})$ で実現することができます。
セグメントツリーは、列を平衡二分木にする ことによって利便性をあげているデータ構造といえます。
オイラーツアー
逆に、木を列にする ということも考えられます。
オイラーツアーがそれにあたります。(正確には「DFS によるオイラーツアー」みたいな言い方が適当らしいですが、競プロ方言的には、この方法を指すことが多いです)
これは、DFS の行きがけ順や帰りがけの順番を記録していくことです。頂点の重さや辺の重さを載せることによって色々なクエリに対応できます。
列にした後はセグ木なり遅延セグ木に載せてクエリを処理するので、結局これも最終的には平衡二分木を使って便利にしていることになります。
HL分解
私にはまだ履修する機会も活用する機会もないですが、解説を読む限り HL分解 も、
- 木を列に分解する
- パスの最大長を抑えることによって最悪計算量を抑える
という点で、これと共通する話だと思います。(違っていたらごめんなさい)
UnionFind木
UnionFind 木が高速なのも、union_by_size(または union_by_rank)によって高さを抑えているからです。
なお、実際の UnionFind 木は、これにくわえて経路圧縮をすることにより更なる高速化を図ってますが、union_by_size だけで $O(\log{N})$ までは高速化できます。
結論
- 木は平衡させることで、色々なクエリを高速で処理できるようになる
- 列は平衡二分木にすることによって、色々なクエリを高速で処理できるようになる
- 便利なデータ構造、だいたい平衡木(極論)
余談
現実のデータベースでも、広く利用されている PostgreSQL や MySQL は B木 という平衡木を使っています。
我々が色々なサービスを高速で使えるのも平衡木のおかげということになります。