コンシステントハッシング法
複数のデータを任意のノードに分散させる場合、データのIDやそのハッシュ値を保存先ノード総数で割るという方法があるが、この方法はノード数自体の変更があった場合にデータ全体のノード間移動が発生してしまうという欠点がある。
そこでノード数の増減時に、必要最低限のデータの移動で済むようなデータの配置方法の一つとしてコンシステントハッシュ法がある。
CassandraやAmazonDynamoのような分散データベースにおいて、データの保存先の決定に使われている。
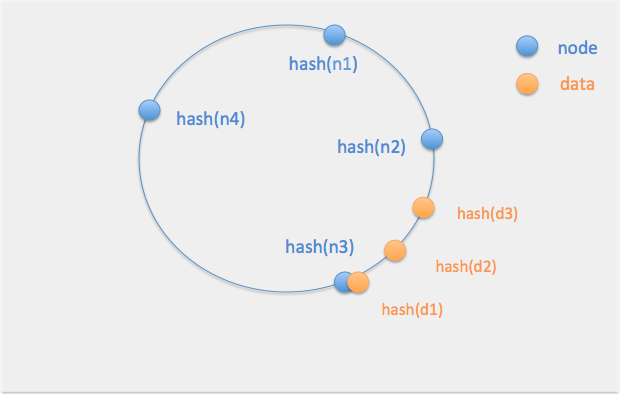
ハッシュ関数を適応したノードとデータをリング状に時計回りに配置し、各ノードは自身と同じかそれより手前に配置されたデータを担当する。
下の図でいうとデータd1-d3はノードn3に保存される。
ざっくりとしたアプローチ
※不足点あればご指摘ください。
データとノードのIDに、大小比較可能な同じハッシュ関数を適応する。
キー(データのID)にハッシュ関数をかける
# 今回はハッシュ関数にmd5を使用
import hashlib
hashed_key = hashlib.md5(str(key)).hexdigest()
ノード(容れ物)側にも同じハッシュ関数をかける
# IDが1~5のノードを用意する
node_ids = range(1, 6)
# (ノードIDのハッシュ値 ,ノードID) のリストを用意
def get_hashed_node_list(node_ids):
"""
:type node_ids: list of int
:rtype list
"""
hashed_node_list = []
for node_id in node_ids:
hashed_node_id = hashlib.md5(str(node_id).encode('utf-8')).hexdigest()
hashed_node_list.append((hashed_node_id, node_id))
# ハッシュ値でソートしておく
return sorted(hashed_node_list, key=lambda n: n[0])
hashed_node_list = get_hashed_node_list(node_ids)
# ノードIDとハッシュ値の対応は以下のようになる
# 1 => c4ca4238a0b923820dcc509a6f75849b
# 2 => c81e728d9d4c2f636f067f89cc14862c
# 3 => eccbc87e4b5ce2fe28308fd9f2a7baf3
# 4 => e4da3b7fbbce2345d7772b0674a318d5
# 5 => e4da3b7fbbce2345d7772b0674a318d5
ノードをリング状に配置する
以下の順番でデータを割り当てるノードを決定する
- キーと同じハッシュ値のノード
- キーより大きいハッシュ値を持つノードの中で、ハッシュ値が最小のノード
- ハッシュ値が最小のノード
def get_node_id(hashed_key, hashed_node_list):
"""
:type hashed_key: str
:type hashed_slots: list of (hashed_node_id, node_id)
:rtype int
"""
for hashed_node_id, node_id in hashed_node_list:
if hashed_key == hashed_node_id:
# 1. キーと同じハッシュ値のノード
return node_id
if hashed_key < hashed_node_id:
# 2. キーより大きいハッシュ値を持つノードの中で、ハッシュ値が最小のノード
return node_id
# 3. どれにもヒットしなければハッシュ値が最小のノード
return hashed_nodes[0][1]
データを追加する
key_list = range(1, 21)
nodes = {i: [] for i in range(1, 6)}
hashed_node_list = get_hashed_node_list(nodes.keys())
for key in key_list:
hashed_key = hashlib.md5(str(key).encode('utf-8')).hexdigest()
target_node_id = get_node_id(hashed_key, hashed_node_list)
nodes[target_node_id].append(key)
仮にデータのキーが1~20のシーケンシャルなIDとすると、各ノードへの割当ては以下のようになる
for k, v in nodes.items():
print('{} {}'.format(k, v))
1 [1, 12, 14]
2 [2, 13, 16]
3 [3]
4 [4, 6, 7, 9, 11, 15, 17, 18, 19, 20]
5 [5, 8, 10]

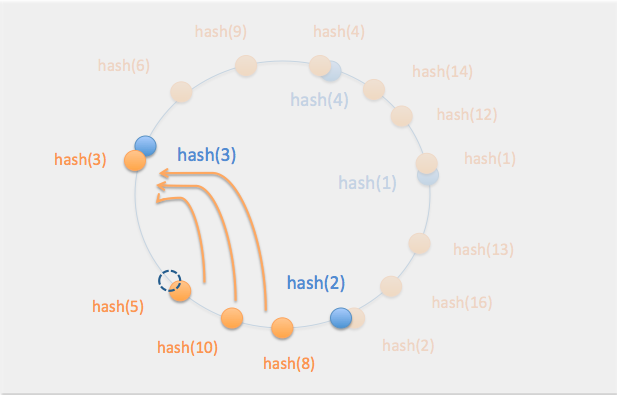
ここから5のノードを抜くと...
1 [1, 12, 14]
2 [2, 13, 16]
3 [3, 5, 8, 10]
4 [4, 6, 7, 9, 11, 15, 17, 18, 19, 20]
ノード5のデータ(5, 8, 10)のみが隣のノード3に移動する
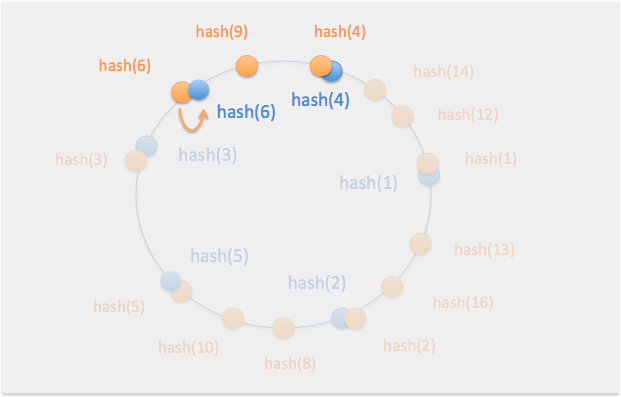
また、ノード6を追加すると...
1 [1, 12, 14]
2 [2, 13, 16]
3 [3]
4 [4, 7, 9, 11, 15, 17, 18, 19, 20]
5 [5, 8, 10]
6 [6]
欠点として、全体のノード数が少ない段階では各ノードにデータの偏りが発生するという点がある。
そのため、仮想ノードを間に配置することでデータをなるべく均等に配置する方法がセットで使用される。
仮想ノード
そのうち追記します。