今回は、太陽の位置を天文学的に正確に計算する C# スクリプトについて詳しく解説します。このスクリプトでは、地球上の任意の位置(緯度・経度)から見た太陽の高度角と方位角を求めます。
対象読者
- 太陽の高度角・方位角を自力で求めたい方
- Unity や OpenGL などで天体シミュレーションを行いたい方
- 太陽追跡や日照シミュレーションに応用したい方
なぜ太陽の位置計算が必要なのか
太陽の位置計算、つまり特定の時刻と場所における太陽の高度角(地平線からの角度)と方位角(北を基準とした水平方向の角度)を求めることは、さまざまな分野で重要な役割を果たします。この計算は、天文学的な興味だけでなく、実生活や技術応用においても不可欠です。
以下に、太陽の位置計算が必要とされる主な理由とその応用例を挙げます。
-
太陽光発電とエネルギー管理
太陽光パネルを最適な角度に調整することで、発電効率を最大化できます。高度角・方位角の予測により、固定式や追尾式のパネルの設計・制御が可能になります。 -
建築設計と環境配慮
日射取得や遮蔽を考慮して建物の方位や窓の配置を決めることで、冷暖房負荷の軽減につながります。パッシブソーラーデザインにも応用されます。 -
天文観測とナビゲーション
天体観測や望遠鏡の自動追尾に使われるほか、GPS が使えない場面では太陽の位置による航法がバックアップになります。 -
AR やゲーム開発
AR アプリやゲームエンジンで現実と連動したライティングや影の表現を実現できます。 -
農業と気象予報
作物の成長や日照量予測に活用できます。温室設計や気象モデルの構築にも役立ちます。
太陽位置計算の流れ
与えられた観測日時・緯度・経度から、太陽の高度角($h$)と方位角($A$)を計算します。
この計算は、天文学で定義された一連のアルゴリズムに基づき、誤差 1° 以内の精度で太陽の見かけの位置を求めます。
以下の流れに沿って、すべてのステップの数式と処理内容を詳細に解説していきます。

- 1 入力パラメータ
- 2 ユリウス日(
JD: Julian Day)の計算 - 3 世紀単位時間(
JC: Julian Century)の算出 - 4 太陽の黄経
- 5 地球の軌道傾斜角(
ε: Obliquity of the Ecliptic) - 6 赤道座標系
- 7 恒星時
- 8 時角(
HA: Hour Angle) - 9 太陽の高度角・方位角
1 入力パラメータ
| 項目 | データ型 | 値(例) |
|---|---|---|
| 日時 (JST) | DateTime | 2025/07/27 12:00 |
| 観測地点の緯度 [°] | double | 35.6895 |
| 観測地点の経度 [°] | double | 139.6917 |
2 ユリウス日(JD: Julian Day)の計算
天文学では、日時をユリウス日(JD)という連続した日数で表現します。JD とは、紀元前 4713 年 1 月 1 日(ユリウス暦)正午(UTC)を起点とした連続した日数を表す数値です。
例えば、
- 2000/1/1 12:00(UTC)は、ユリウス日では
2451545.0となる - 整数部分は、起点からの「日数」
- 小数点以下はその日の経過時間を表します。例えば、
0.5加算した2451545.5は翌日の 0:00 となる
JD は西暦よりも誤差が少なく、数値計算に適しているため、天体の運動や観測データの処理で広く使われるものとなっています。
数式:
JD の計算式は以下の通りです(グレゴリオ暦)。
\begin{align*}
&\text{if } M \leq 2: \; Y = Y - 1,\, M = M + 12 \\
&\qquad A = \left\lfloor \frac{Y}{100} \right\rfloor \\
&\qquad B = 2 - A + \left\lfloor \frac{A}{4} \right\rfloor \\
&\qquad JD = \left\lfloor 365.25 \times (Y + 4716) \right\rfloor + \left\lfloor 30.6001 \times (M + 1) \right\rfloor + D + B - 1524.5 + \frac{h}{24}
\end{align*}
- $Y$:年
- $M$:月
- $D$:日
- $h$:時刻(小数)
- $A$:西暦 $Y$ の世紀
- $B$:レゴリオ暦補正項(グレゴリオ暦が導入された1582年以降、閏年ルールの修正を反映する補正値)
- $365.25 × (Y + 4716)$:年を日数に変換(うるう年も考慮)
- $30.6001 × (M + 1)$:J2000.0 に合わせるための原点調整
- J2000.0 は、2000/1/1 12:00:00(UTC)で、ユリウス世紀($JC$: Julian Century)の起点でもある
- 天文学では、天体の位置は時間とともに変化するため、基準となる時刻を決めておく必要がある
- $h/24$:小数で時刻(時間)を加算
$\text{if } M \leq 2: \hspace{8px} Y = Y - 1, \hspace{4px} M = M + 12$ は、月が 1 月または 2 月の場合に年を 1 減らし、月に 12 加えることで、1 月を前年の 13 月、2 月を前年の 14 月として扱います。
これにより、うるう年(2 月 29 日)の影響を最小化することができます。
C# 実装:
タイムゾーンを世界基準である UTC に変換後、ユリウス日に変換します。
DateTime utc = dateTime.ToUniversalTime();
double hour = utc.Hour + utc.Minute / 60.0 + utc.Second / 3600.0;
int year = utc.Year;
int month = utc.Month;
int day = utc.Day;
if (month <= 2) { year -= 1; month += 12; }
int A = year / 100;
int B = 2 - A + A / 4;
double JD = Math.Floor(365.25 * (year + 4716)) +
Math.Floor(30.6001 * (month + 1)) +
day + B - 1524.5 + hour / 24.0;
3 世紀単位時間(JC: Julian Century)の算出
JC はユリウス日($JD$)に基づいた時刻を 2000 年 1 月 1 日 12 時(UTC)からのユリウス世紀数で表した値です。
数式:
JC = \frac{JD - 2451545.0}{36525.0}
- $JD$:ユリウス日
- $2451545.0$:2000 年 1 月 1 日 12 時(J2000.0) のユリウス日
- $36525.0$:1 ユリウス世紀の日数(365.25 日 × 100 年)
C# 実装:
double JC = (JD - 2451545.0) / 36525.0;
4 太陽の黄経
黄経とは、黄道と春分点を基準として、天球上にある天体の位置を示す黄道座標の経度です。

(出典:コトバンク)
4.1 太陽の平均黄経(L: Mean Longitude)
これは、太陽の平均黄経(Mean Longitude of the Sun)を求める式で、太陽がもし等速で円軌道を公転していると仮定した場合の黄道上の位置を計算します。
数式:
平均黄経 $L$ を算出後、360° で正規化します。
\begin{align}
&L = 280.46646 + JC \times (36000.76983 + JC \times 0.0003032) \\
&L = L \bmod 360^\circ
\end{align}
- $JC$:世紀単位時間
- $280.46646$:J2000.0(2000年1月1日12時UT)における太陽の平均黄経(度)
- 春分点から見て、地球が見かけ上黄道上で約 280.47 度の位置にあることを示す(≒冬至頃)
- $36000.76983$:JC(1 ユリウス世紀)あたりの平均黄経の増加量(度/世紀)
- 地球の公転により、太陽の見かけ位置は年々移動するので、基準点からの進みを反映
- $0.0003032$:地球の公転軌道の摂動や歳差運動による微小な変化を補正
- 公転速度や歳差運動による微小な長期変化を考慮
C# 実装:
double L = 280.46646 + JC * (36000.76983 + JC * 0.0003032);
L %= 360.0;
4.2 平均近点角(M: Mean Anomaly)
平均近点角とは、天体が等速で円軌道を公転していると仮定したとき、近日点(最も近い点)から何度進んだかを角度で表したものです。0° は近日点(最近い点)、180° は遠日点(最も遠い点)を意味します。
数式:
M = 357.52911 + JC \times (35999.05029 - 0.0001537 \times JC)
- $JC$:世紀単位時間
- $357.52911$:西暦 2000 年 1 月 1 日 12:00(J2000.0)における太陽の平均近点角(度)
- $35999.05029$:平均近点角の年あたりの進み(度/世紀)= 地球の公転平均速度
- $0.0001537$:太陽の軌道要素の長期的なわずかに変化を反映
C# 実装:
double M = 357.52911 + JC * (35999.05029 - 0.0001537 * JC);
4.3 離心率補正(C: Equation of Center)
離心率補正とは、楕円軌道における平均近点角(M)と真の角度(真近点角)との差を補正する角度です。
地球の公転軌道は楕円形なので、実際の動きは加減速するのですが、この加減速によるズレ(楕円軌道の非対称性)を補う補正項となります。
数式:
\begin{align*}
C = &(1.914602 - JC \times (0.004817 + 0.000014 \times JC)) \sin(M) + \\
&(0.019993 - 0.000101 \times JC) \sin(2M) + \\
&0.000289 \sin(3M) \\
\end{align*}
- $1.914602$:地球の軌道の離心率(約 $0.0167$)に由来し、主な補正成分
- $JC$:世紀単位時間
- $0.004817$, $0.000014$:JC による経年変化補正項
- $M$:上記で求めた平均近点角(単位:度)
- $\sin(nM)$:$n$ 倍角の正弦で、軌道の非円形度(離心率)に伴う補正を段階的に加えるための項
- $0.019993$:軌道の楕円性に起因
- $0.000101$:経年変化補正項
- $0.000289$:微小な非線形補正を行う
C# 実装:
double C = (1.914602 - JC * (0.004817 + 0.000014 * JC)) * Math.Sin(DegToRad(M)) +
(0.019993 - 0.000101 * JC) * Math.Sin(DegToRad(2 * M)) +
0.000289 * Math.Sin(DegToRad(3 * M));
4.4 真黄経(λ: True Longitude)
真黄経とは、実際の軌道運動に基づいた、現在の正確な黄道上の位置(角度)で、楕円軌道や公転の加減速を考慮して求めます。
数式:
\lambda = L + C
- $L$:太陽の平均黄経
- $C$:離心率補正
C# 実装:
double trueLongitude = L + C;
5 地球の軌道傾斜角(ε: Obliquity of the Ecliptic)
地球の軌道傾斜角とは、地球の赤道面と黄道面(太陽の見かけの通り道)のなす角度のことで、通常「地球の自転軸の傾き」や「地軸の傾斜」とも呼ばれます。
数式:
\epsilon = 23.439291 - 0.0130042 \times JC
- $23.439291$:J2000.0(2000年1月1日)における地球の軌道傾斜角(単位:度)
- 地球の自転軸が赤道に対して23.44度傾いていることを表す
- $0.0130042$:JCあたりの減少量(単位:度/世紀)
- 地球の歳差運動により軌道傾斜角が非常にゆっくり減少している現象を反映
- $JC$:世紀単位時間
※ 歳差運動により、地球の軌道傾斜角は約41,000年周期で21.5°~24.5°の間を変動しています。
C# 実装:
double epsilon = 23.439291 - 0.0130042 * JC;
double lambda = DegToRad(trueLongitude);
double obliquity = DegToRad(epsilon);
6 赤道座標系
赤道座標系とは、天体の位置を表すための天球上の座標系のことを指します。
赤道座標系を求めることにより、その日の日の出・日の入り時刻や南中高度・方位に使うことができるようになります。
6.1 赤経(α: Right Ascension)
赤経は、天球上の東西方向の角度で、春分点(太陽が春分の時にある点)を起点として、天の赤道に沿って東向きに測った角度となります。
数式:
\alpha = \arctan2(\cos(\epsilon) \sin(\lambda), \cos(\lambda))
- $\epsilon$:地球の軌道傾斜角
- $\cos(\epsilon)$:軌道傾斜角によって黄道と赤道の間に生じる傾きを反映する項
- $\lambda$:真黄経
- $\sin(\lambda)$:黄道上の太陽位置の東西成分
- $\cos(\lambda)$:黄道上の太陽位置の南北成分
※ $\arctan2$ 関数により、-180°~180° の範囲で正確に方向を判断できます。
C# 実装:
double alpha = Math.Atan2(Math.Cos(obliquity) * Math.Sin(lambda), Math.Cos(lambda));
6.2 赤緯(δ: Declination)
赤緯とは、天球上の南北方向の角度です。天の赤道を 0° として、北に向かって正 (+)、南に向かって負 (−) に測ります。
数式:
\delta = \arcsin(\sin(\epsilon) \sin(\lambda))
- $\epsilon$:地球の軌道傾斜角
- $\sin(\epsilon)$:軌道傾斜角に基づく黄道の傾き
- $\lambda$:真黄経
- $\sin(\lambda)$:黄道上での太陽位置
※ 夏至では $λ ≈ 90°$であり、このとき $δ ≈ +23.4°$(北回帰線)
冬至では $λ ≈ 270°$であり、このとき $δ ≈ -23.4°$(南回帰線)
C# 実装:
double delta = Math.Asin(Math.Sin(obliquity) * Math.Sin(lambda));
7 恒星時
恒星時とは、恒星(背景の遠方天体)を基準に定義された時刻で、太陽ではなく宇宙全体の背景との関係で地球の自転を測る基準です。
1 恒星日は、地球が恒星に対して1回転するのにかかる時間(約 23 時間 56 分 4秒)です。
7.1 グリニッジ恒星時(GST: Greenwich Sidereal Time)
グリニッジ恒星時は、地球全体で共通に使われる恒星時の基準です。
天体の赤経と連携して、子午線通過(南中)のタイミングを判定するのに使われます。
J2000.0 を基準とした時刻(ユリウス日 $JD$)から、数学的に正確に求めることができます。
数式:
GST = 280.46061837 + 360.98564736629 \times (JD - 2451545.0)
- $280.46061837$:J2000.0 におけるグリニッジ恒星時の初期値(度)
- $360.98564736629$:1日あたりの地球の自転角度(恒星時)(度/日)
- 1 太陽日(24 時間)より少し速く 1 回転する値
- $JD$:ユリウス日
- $JD - 2451545.0$:J2000.0 からの経過日数(ユリウス日差)
※ 恒星日は約 23 時間 56 分 4 秒(≒ 0.997269日)で 1 回転
⇒ 1 日あたり約 360.985 度回転
C# 実装:
double GST = 280.46061837 + 360.98564736629 * (JD - 2451545.0);
7.2 観測地点での恒星時(LST: Local Sidereal Time)
観測者がいる任意の地点(経度 $λ$)での恒星時です。
グリニッジ恒星時にその地点の経度(東経なら +、西経なら −)を加えたものとなります。
数式:
LST = (GST + \text{longitude}) \mod 360
- $longitude$:観測者の経度(東経は $+$、西経は $−$)
- $mod\hspace{0.5em}360$:0〜360 度の範囲に正規化
C# 実装:
double LST = (GST + longitude) % 360.0;
if (LST < 0) LST += 360.0;
8 時角(HA: Hour Angle)
時角は、観測地点での現在の時刻における太陽の位置を示します。

(出典:暦Wiki)
数式:
HA = LST - \alpha
(ラジアンに変換し、$-\pi$〜$\pi$ の範囲に正規化)
- $LST$:その地点の恒星時
- $\alpha$:太陽の赤経
※ $HA = 0$:太陽がその地点の子午線を通過(=南中)
$HA < 0$:太陽はこれから南中する(東側)
$HA > 0$:太陽は南中を過ぎている(西側)
C# 実装:
double HA = DegToRad(LST) - alpha;
while (HA < -Math.PI) HA += 2 * Math.PI;
while (HA > Math.PI) HA -= 2 * Math.PI;
9 太陽の高度角・方位角
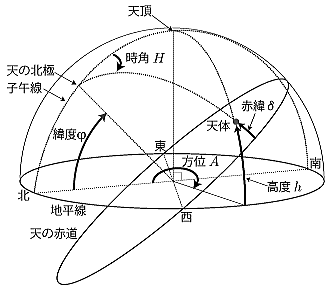
(出典:太陽の方位・高度と出現月日)
9.1 高度角(h: Altitude)
高度角は、太陽がどの高さにあるかを示します。
数式:
\sin(h) = \sin(longitude) \sin(\delta) + \cos(longitude) \cos(\delta) \cos(HA)
h = \arcsin(\sin(h))
- $HA$:時角
- $longitude$:観測地点の経度(北緯:$+$、南緯:$−$)
- $\delta$:赤緯
C# 実装:
double latRad = DegToRad(latitude);
double altitudeRad = Math.Asin(Math.Sin(latRad) * Math.Sin(delta) +
Math.Cos(latRad) * Math.Cos(delta) * Math.Cos(HA));
float altitudeDeg = (float)RadToDeg(altitudeRad);
9.2 方位角(A: Azimuth)
方位角は、太陽がどの方向にあるかを示します。
北を 0° とし、東回り(時計回り)で定義します。
数式:
A = \arctan2(\sin(HA), \cos(HA)\sin(longitude) - \tan(\delta)\cos(longitude))
- $HA$:時角
- $longitude$:観測地点の経度(北緯:$+$、南緯:$−$)
- $\delta$:赤緯
C# 実装:
double azimuthRad = Math.Atan2(Math.Sin(HA),
Math.Cos(HA) * Math.Sin(latRad) - Math.Tan(delta) * Math.Cos(latRad));
float azimuthDeg = (float)((RadToDeg(azimuthRad) + 180.0) % 360.0);
精度評価
国立天文台の太陽系天体の高度と方位の値を基準として、今回の実装を用いて導き出した値の精度評価を行ってみます。
今回対象とする日付および緯度経度は以下とします。
- 日付:2025/7/28
- 緯度:35.6586
- 経度:139.7454
算出値と国立天文台の値、およびそれらの誤差は以下の通りです。
方位角 (Azimuth)データ
| 時刻 | 算出値 | 国立天文台の値 | 誤差 |
|---|---|---|---|
| 0:00 | 3.59 | 3.5947 | -0.00470000000000015 |
| 1:00 | 20.422 | 20.4253 | -0.00329999999999941 |
| 2:00 | 35.396 | 35.3981 | -0.00209999999999866 |
| 3:00 | 48.034 | 48.0349 | -0.000900000000001455 |
| 4:00 | 58.631 | 58.6321 | -0.00110000000000099 |
| 5:00 | 67.766 | 67.7663 | -0.000299999999995748 |
| 6:00 | 76.046 | 76.0457 | 0.000300000000009959 |
| 7:00 | 84.091 | 84.0906 | 0.000399999999999068 |
| 8:00 | 92.667 | 92.6663 | 0.000699999999994816 |
| 9:00 | 103.044 | 103.0439 | 0.00010000000000332 |
| 10:00 | 118.03 | 118.0312 | -0.0011999999999972 |
| 11:00 | 144.738 | 144.7437 | -0.00569999999999027 |
| 12:00 | 190.125 | 190.139 | -0.01400000000001 |
| 13:00 | 228.444 | 228.4558 | -0.0118000000000222 |
| 14:00 | 248.981 | 248.989 | -0.00800000000000978 |
| 15:00 | 261.521 | 261.5267 | -0.00569999999999027 |
| 16:00 | 270.928 | 270.9333 | -0.00529999999997699 |
| 17:00 | 279.163 | 279.1679 | -0.00489999999996371 |
| 18:00 | 287.217 | 287.2218 | -0.00479999999998881 |
| 19:00 | 295.77 | 295.7741 | -0.004099999999994 |
| 20:00 | 305.43 | 305.4343 | -0.00430000000000064 |
| 21:00 | 316.81 | 316.8152 | -0.00520000000000209 |
| 22:00 | 330.428 | 330.4333 | -0.00529999999997699 |
| 23:00 | 346.334 | 346.3389 | -0.00490000000002055 |
高度角 (Altitude) データ
| 時刻 | 算出値 | 国立天文台の値 | 誤差 |
|---|---|---|---|
| 0:00 | -35.211 | -35.2095 | -0.00150000000000006 |
| 1:00 | -32.672 | -32.67 | -0.00199999999999534 |
| 2:00 | -26.956 | -26.9542 | -0.00179999999999936 |
| 3:00 | -18.841 | -18.8383 | -0.00270000000000081 |
| 4:00 | -9.067 | -9.0645 | -0.0024999999999995 |
| 5:00 | 1.803 | 2.1013 | -0.2983 |
| 6:00 | 13.376 | 13.4457 | -0.069700000000001 |
| 7:00 | 25.365 | 25.4028 | -0.0378000000000007 |
| 8:00 | 37.532 | 37.5559 | -0.0239000000000047 |
| 9:00 | 49.59 | 49.6073 | -0.0172999999999988 |
| 10:00 | 61.008 | 61.0209 | -0.0128999999999948 |
| 11:00 | 70.264 | 70.2732 | -0.00920000000000698 |
| 12:00 | 73.055 | 73.061 | -0.00600000000000023 |
| 13:00 | 66.869 | 66.8746 | -0.00560000000000116 |
| 14:00 | 56.392 | 56.3999 | -0.00789999999999935 |
| 15:00 | 44.602 | 44.6156 | -0.0136000000000038 |
| 16:00 | 32.447 | 32.4695 | -0.0224999999999937 |
| 17:00 | 20.313 | 20.3533 | -0.040300000000002 |
| 18:00 | 8.451 | 8.5505 | -0.099499999999999 |
| 19:00 | -2.89 | -2.8939 | 0.00389999999999979 |
| 20:00 | -13.388 | -13.3908 | 0.00280000000000058 |
| 21:00 | -22.585 | -22.5873 | 0.00229999999999819 |
| 22:00 | -29.84 | -29.841 | 0.00100000000000122 |
方位角・高度角ともに、平均誤差・最大誤差が 0.3° 未満と非常に小さな誤差となっており、シミュレーション用途としては十分な精度が得られます。
| 項目 | 平均誤差 | 最大誤差 |
|---|---|---|
| 方位角 | -0.0040° | ±0.0140° |
| 高度角 | -0.0277° | ±0.2983° |
留意事項
角度の単位
天文学や軌道計算では、天体の位置を表すデータ(黄経、赤緯、軌道傾斜角など)は、人が直感的に理解しやすい度単位で表されるのに対して、C# の数学ライブラリ(Math.Sin、Math.Cos、Math.Tan)の入力はラジアンとなります。
そのため、必要に応じて**度からラジアンへの変換(DegToRad 関数)やラジアンから度への変換(RadToDeg 関数)を行っています。
private static double DegToRad(double deg) => deg * Math.PI / 180.0;
private static double RadToDeg(double rad) => rad * 180.0 / Math.PI;
方位角・高度角の精度
アルゴリズムは Astronomical Almanac の低精度版を基にしており、1950-2050 年の範囲で方位角・高度角の誤差が約 1° 以内です。高精度が必要な場合は NREL の Solar Position Algorithm (SPA) を検討してください(誤差±0.0003°)
J2000.0 基準と歳差運動の影響
このスクリプトは J2000.0(2000 年 1 月 1 日 12:00 UTC)を基準とした定数を使用しており、1950〜2050 年の範囲では高度角・方位角の誤差が約 1° 以内に収まります。ただし、地球の歳差運動(春分点の移動や軌道傾斜角の変動)により、2100 年以降は誤差が徐々に増大します。たとえば、2100 年では春分点の約 1.4° のずれにより、太陽の高度角・方位角に 1〜2° の誤差が生じる可能性があります。2200 年以降ではさらに誤差が拡大(3° 以上)する可能性があるため、長期的な計算では以下を検討してください:
- 高精度アルゴリズムの採用:NREL の Solar Position Algorithm (SPA) や VSOP モデルを使用すると、誤差を 0.0003° 以内に抑えることも可能
- 定数の更新:2100 年以降の計算では、最新の天文データに基づく定数更新が必要となる
- 外部ライブラリ:AstroLib や Skyfield(Python だが C# に移植可能)を使用し、最新の歳差・章動モデルを適用
参考文献
- Julian Day Numbers, Bill Jefferys
- NREL. Solar Position Algorithm for Solar Radiation Applications. 2008
- コトバンク
- James Still. Astronomical Calculations: Solar Coordinates. 2019
- イワクラ(磐座)学会. 太陽の方位・高度と出現月日. 2018
- Wikipedia. VSOP model
- PyAstronomy. Position of the Sun
- Rhodes Mill. Skyfield