本記事はゼロから作るDeep Learningなどを参考にしています。
デモ用のコードはこちらです。
学習
深層学習では次のようなモデルを考える。
L=f(\boldsymbol{x};\boldsymbol{\theta})
ここで、各文字は次のように定義される。
$L$ : 損失
$f$ : モデル
$\boldsymbol{x}$ : 入力値
$\boldsymbol{\theta}$ : パラメータ
損失が小さくなるようにモデル$f$の学習を行う。
モデル$f$の学習は次のようにパラメータ$\boldsymbol{\theta}$を更新することで実現される。
\boldsymbol{\theta_{new}}=\boldsymbol{\theta_{old}} - \eta \frac{\partial L}{\partial \boldsymbol{\theta_{old}}}, \quad \eta > 0
ここで、$\eta$は学習率と呼ばれるハイパーパラメータである。
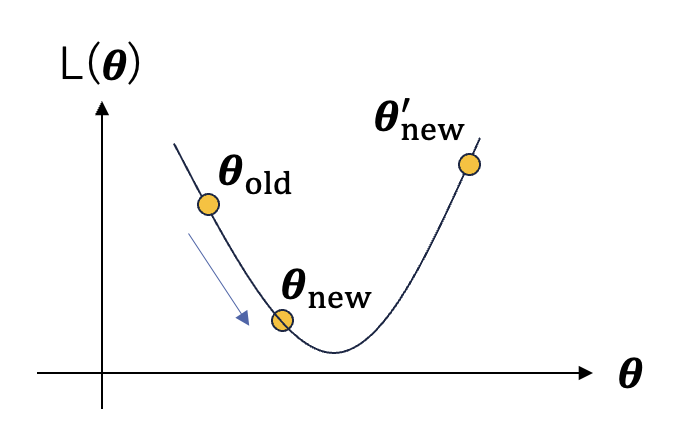
例として、上図のような場合を考える。
$\frac{\partial L}{\partial \boldsymbol{\theta_{old}}} < 0$であるため、パラメータの更新を行うと、$L(\boldsymbol{\theta_{old}})>L(\boldsymbol{\theta_{new}})$となり、損失が小さくなっていることが分かる。
ただし、学習率$\eta$や勾配$\frac{\partial L}{\partial \boldsymbol{\theta_{old}}}$が大きいと、パラメータが$\boldsymbol{\theta_{new}^{'}}$へと更新され、$L(\boldsymbol{\theta_{old}})<L(\boldsymbol{\theta_{new}^{'}})$となってしまい、むしろ損失が大きくなってしまう。
このように、必ずしもパラメータの更新を行うことによって損失が小さくなるわけでない。
連鎖律
上述したように、深層学習ではパラメータの更新を行うために勾配を求める必要がある。そこで、連鎖律を用いて勾配を効率的に算出する。
ここでは、次のようなモデルを考える。
L = L(z), \quad z = z(y, \theta_{y}), \quad y = y(x, \theta_{x})
勾配は連鎖律を用いて次のように計算できる。
\begin{align}
\frac{\partial L}{\partial \theta_{y}} &= \frac{\partial L}{\partial z}\frac{\partial z}{\partial \theta_{y}} \\
\frac{\partial L}{\partial y} &= \frac{\partial L}{\partial z}\frac{\partial z}{\partial y} \\
\frac{\partial L}{\partial \theta_{x}} &= \frac{\partial L}{\partial z}\frac{\partial z}{\partial y}\frac{\partial y}{\partial \theta_{x}} = \frac{\partial L}{\partial y}\frac{\partial y}{\partial \theta_{x}} \\
\frac{\partial L}{\partial x} &= \frac{\partial L}{\partial z}\frac{\partial z}{\partial y}\frac{\partial y}{\partial x} = \frac{\partial L}{\partial y}\frac{\partial y}{\partial x}\\
\end{align}
全結合層
下図のような全結合層を考える。

$\boldsymbol{x}$,$\boldsymbol{y}$,$W$を次のように定義する。
\boldsymbol{x}=\begin{pmatrix}
x_{1} \\
x_{2}
\end{pmatrix}
\boldsymbol{y}=\begin{pmatrix}
y_{1} \\
y_{2} \\
y_{3}
\end{pmatrix}
W = \begin{pmatrix}
w_{11} & w_{12} & w_{13} \\
w_{21} & w_{22} & w_{23} \\
\end{pmatrix}
順伝播は下記のように表せる。
\begin{align}
\boldsymbol{y}^{t} &= \begin{pmatrix}
y_1 & y_2 & y_3
\end{pmatrix} \\
&= \begin{pmatrix}
x_{1}w_{11} + x_{2}w_{21} & x_{1}w_{12} + x_{2}w_{22} & x_{1}w_{13} + x_{2}w_{23}
\end{pmatrix} \\
&= \begin{pmatrix}
x_{1} & x_{2}
\end{pmatrix}
\begin{pmatrix}
w_{11} & w_{12} & w_{13} \\
w_{21} & w_{22} & w_{23} \\
\end{pmatrix} \\
&= \boldsymbol{x}^{t} W
\end{align}
次に、逆伝播について考える。
L = L(y_{1},y_{2},y_{3})
であるとする。
\begin{align}
y_{1} = y_{1}(x_{1},x_{2},w_{11},w_{21}) = x_{1}w_{11} + x_{2}w_{21} \\
y_{2} = y_{2}(x_{1},x_{2},w_{12},w_{22}) = x_{1}w_{12} + x_{2}w_{22} \\
y_{3} = y_{3}(x_{1},x_{2},w_{13},w_{23}) = x_{1}w_{13} + x_{2}w_{23}
\end{align}
であることに注意して、連鎖律を用いると、
\begin{align}
\frac{\partial L}{\partial \boldsymbol{x}^{t}}
&=
\begin{pmatrix}
\frac{\partial L}{\partial x_{1}} & \frac{\partial L}{\partial x_{2}}
\end{pmatrix} \\
&= \begin{pmatrix}
\frac{\partial L}{\partial y_{1}}\frac{\partial y_{1}}{\partial x_{1}}
+\frac{\partial L}{\partial y_{2}}\frac{\partial y_{2}}{\partial x_{1}}
+\frac{\partial L}{\partial y_{3}}\frac{\partial y_{3}}{\partial x_{1}} &
\frac{\partial L}{\partial y_{1}}\frac{\partial y_{1}}{\partial x_{2}}
+\frac{\partial L}{\partial y_{2}}\frac{\partial y_{2}}{\partial x_{2}}
+\frac{\partial L}{\partial y_{3}}\frac{\partial y_{3}}{\partial x_{2}}
\end{pmatrix} \\
&= \begin{pmatrix}
\frac{\partial L}{\partial y_{1}} w_{11}
+\frac{\partial L}{\partial y_{2}} w_{12}
+\frac{\partial L}{\partial y_{3}} w_{13} &
\frac{\partial L}{\partial y_{1}} w_{21}
+\frac{\partial L}{\partial y_{2}} w_{22}
+\frac{\partial L}{\partial y_{3}} w_{23}
\end{pmatrix} \\
&= \begin{pmatrix}
\frac{\partial L}{\partial y_{1}} & \frac{\partial L}{\partial y_{2}} & \frac{\partial L}{\partial y_{3}}
\end{pmatrix}
\begin{pmatrix}
w_{11} & w_{21} \\
w_{12} & w_{22} \\
w_{13} & w_{23} \\
\end{pmatrix} \\
&= \frac{\partial L}{\partial \boldsymbol{y}^{t}} W^{t}
\end{align}
と表せる。
また、
\begin{align}
\frac{\partial L}{\partial w_{ij}}
&= \frac{\partial L}{\partial y_{1}}\frac{\partial y_{1}}{\partial w_{ij}}
+ \frac{\partial L}{\partial y_{2}}\frac{\partial y_{2}}{\partial w_{ij}}
+ \frac{\partial L}{\partial y_{3}}\frac{\partial y_{3}}{\partial w_{ij}} \\
&= \frac{\partial L}{\partial y_{1}}\frac{\partial (x_{1}w_{11} + x_{2}w_{21})}{\partial w_{ij}}
+ \frac{\partial L}{\partial y_{2}}\frac{\partial (x_{1}w_{12} + x_{2}w_{22})}{\partial w_{ij}}
+ \frac{\partial L}{\partial y_{3}}\frac{\partial (x_{1}w_{13} + x_{2}w_{23})}{\partial w_{ij}} \\
&= \frac{\partial L}{\partial y_{j}} x_{i}
\end{align}
となるので、
\begin{align}
\frac{\partial L}{\partial W}
&= \begin{pmatrix}
\frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{13}} \\
\frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}} & \frac{\partial L}{\partial w_{23}}
\end{pmatrix} \\
&= \begin{pmatrix}
\frac{\partial L}{\partial y_{1}} x_{1} & \frac{\partial L}{\partial y_{2}} x_{1} & \frac{\partial L}{\partial y_{3}} x_{1} \\
\frac{\partial L}{\partial y_{1}} x_{2} & \frac{\partial L}{\partial y_{2}} x_{2} & \frac{\partial L}{\partial y_{3}} x_{2}
\end{pmatrix} \\
&= \begin{pmatrix}
x_{1} \\
x_{2}
\end{pmatrix}
\begin{pmatrix}
\frac{\partial L}{\partial y_{1}} & \frac{\partial L}{\partial y_{2}} & \frac{\partial L}{\partial y_{3}}
\end{pmatrix} \\
&=
\begin{pmatrix}
\boldsymbol{x}^{t}
\end{pmatrix}^{t}
\frac{\partial L}{\partial \boldsymbol{y}^{t}}
\end{align}
と表せる。
これまでの議論の自然な拡張としてバッチ化を行う。
$X$,$Y$を次のように定義する。
X = \begin{pmatrix}
x_{11} & x_{12} \\
x_{21} & x_{22}
\end{pmatrix}
Y = \begin{pmatrix}
y_{11} & y_{12} & y_{13} \\
y_{21} & y_{22} & y_{23}
\end{pmatrix}
それぞれの行列において、1行目が1つ目のサンプルに、2行目が2つ目のサンプルに対応している。
順伝播は次のように表せる。
\begin{align}
Y &= \begin{pmatrix}
y_{11} & y_{12} & y_{13} \\
y_{21} & y_{22} & y_{23}
\end{pmatrix} \\
&= \begin{pmatrix}
x_{11}w_{11} + x_{12}w_{21} & x_{11}w_{12} + x_{12}w_{22} & x_{11}w_{13} + x_{12}w_{23} \\
x_{21}w_{11} + x_{22}w_{21} & x_{21}w_{12} + x_{22}w_{22} & x_{21}w_{13} + x_{22}w_{23}
\end{pmatrix} \\
&= \begin{pmatrix}
x_{11} & x_{12} \\
x_{21} & x_{22}
\end{pmatrix}
\begin{pmatrix}
w_{11} & w_{12} & w_{13} \\
w_{21} & w_{22} & w_{23} \\
\end{pmatrix} \\
&= XW
\end{align}
逆伝播は次のように表せる。
\begin{align}
\frac{\partial L}{\partial X}
&= \begin{pmatrix}
\frac{\partial L}{\partial x_{11}} & \frac{\partial L}{\partial x_{12}} \\
\frac{\partial L}{\partial x_{21}} & \frac{\partial L}{\partial x_{22}}
\end{pmatrix} \\
&= \begin{pmatrix}
\frac{\partial L}{\partial y_{11}}w_{11} + \frac{\partial L}{\partial y_{12}}w_{12} + \frac{\partial L}{\partial y_{13}}w_{13} & \frac{\partial L}{\partial y_{11}}w_{21} + \frac{\partial L}{\partial y_{12}}w_{22} + \frac{\partial L}{\partial y_{13}}w_{23} \\
\frac{\partial L}{\partial y_{21}}w_{11} + \frac{\partial L}{\partial y_{22}}w_{12} + \frac{\partial L}{\partial y_{23}}w_{13} & \frac{\partial L}{\partial y_{21}}w_{21} + \frac{\partial L}{\partial y_{22}}w_{22} + \frac{\partial L}{\partial y_{23}}w_{23}
\end{pmatrix} \\
&= \begin{pmatrix}
\frac{\partial L}{\partial y_{11}} & \frac{\partial L}{\partial y_{12}} & \frac{\partial L}{\partial y_{13}} \\
\frac{\partial L}{\partial y_{21}} & \frac{\partial L}{\partial y_{22}} & \frac{\partial L}{\partial y_{23}}
\end{pmatrix}
\begin{pmatrix}
w_{11} & w_{21} \\
w_{12} & w_{22} \\
w_{13} & w_{23} \\
\end{pmatrix} \\
&= \frac{\partial L}{\partial Y} W^{t}
\end{align}
\begin{align}
\frac{\partial L}{\partial W}
&= \begin{pmatrix}
\frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{13}} \\
\frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}} & \frac{\partial L}{\partial w_{23}}
\end{pmatrix} \\
&= \begin{pmatrix}
\frac{\partial L}{\partial y_{11}} x_{11} + \frac{\partial L}{\partial y_{21}} x_{21} & \frac{\partial L}{\partial y_{12}} x_{11} + \frac{\partial L}{\partial y_{22}} x_{21} & \frac{\partial L}{\partial y_{13}} x_{11} + \frac{\partial L}{\partial y_{23}} x_{21} \\
\frac{\partial L}{\partial y_{11}} x_{12} + \frac{\partial L}{\partial y_{21}} x_{22} & \frac{\partial L}{\partial y_{12}} x_{12} + \frac{\partial L}{\partial y_{22}} x_{22} & \frac{\partial L}{\partial y_{13}} x_{12} + \frac{\partial L}{\partial y_{23}} x_{22}
\end{pmatrix} \\
&= \begin{pmatrix}
x_{11} & x_{21} \\
x_{12} & x_{22}
\end{pmatrix}
\begin{pmatrix}
\frac{\partial L}{\partial y_{11}} & \frac{\partial L}{\partial y_{12}} & \frac{\partial L}{\partial y_{13}} \\
\frac{\partial L}{\partial y_{21}} & \frac{\partial L}{\partial y_{22}} & \frac{\partial L}{\partial y_{23}}
\end{pmatrix} \\
&= X^{t} \frac{\partial L}{\partial Y}
\end{align}
Relu

Relu関数は下式で表される。
y = \begin{cases}
x \quad (x \geq 0) \\
0 \quad (x < 0)
\end{cases}
逆伝播は次のように表せる。
\frac{\partial y}{\partial x} = \begin{cases}
1 \quad (x \geq 0) \\
0 \quad (x < 0)
\end{cases}
Softmax
Softmax関数は次のように表される。
y_{i} = f_{softmax}(x_{i}) = \frac{exp(x_{i})}{\displaystyle\sum_{j=1}^{D}exp(x_{j})},
ここで、
\boldsymbol{x} = \begin{pmatrix}
x_{1} \\
\vdots \\
x_{D}
\end{pmatrix}, \quad
\boldsymbol{y} = \begin{pmatrix}
y_{1} \\
\vdots \\
y_{D}
\end{pmatrix}
\in \mathbb{R}^{D}
とおいた。
このとき、
\displaystyle\sum_{d=1}^{D}y_{d} = 1, \quad 0 \leq y_{d} \leq 1 \quad for \quad 1 \leq d \leq D
を満たす。
CrossEntorypyLoss
CrossEntropyLossは次のように表される。
L = - \displaystyle\sum_{k=1}^{K}t_{k}log(y_{k})
ここで、$t_{k}$はone-hotベクトルであり、$y_{k}$はクラス$k$である予測確率を表す。
つまり、
\displaystyle\sum_{k=1}^{K}y_{k} = 1, \quad 0 \leq y_{k} \leq 1 \quad for \quad 1 \leq k \leq K
\displaystyle\sum_{k=1}^{K}t_{k} = 1, \quad t_{k} \in \{0, 1\} \quad for \quad 1 \leq k \leq K
を満たす。
バッチ化されている場合は次のように表される。
L = - \frac{1}{N}\displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{K}t_{nk}log(y_{nk})
ここで、$N$はバッチサイズを表す。
Softmax And CrossEntorypyLoss
Softmax関数を適用した後に、CrossEntropyLossを計算する場合を考える。
これは、$K$をクラス数、$\boldsymbol{t}$をone-hotベクトルとすると、
\boldsymbol{x} = \begin{pmatrix}
x_{1} \\
\vdots \\
x_{K}
\end{pmatrix}, \quad
\boldsymbol{y} = \begin{pmatrix}
y_{1} \\
\vdots \\
y_{K}
\end{pmatrix}
\in \mathbb{R}^{K}
y_{k} = f_{softmax}(x_{k}) \quad for \quad 1 \leq k \leq K
\boldsymbol{t} = \begin{pmatrix}
t_{1} \\
\vdots \\
t_{K}
\end{pmatrix}
L = - \displaystyle\sum_{k=1}^{K}t_{k}log(y_{k})
と表せる。
このとき、逆伝播は次のようになることが知られている。
\frac{\partial L}{\partial x_{k}} = y_{k} - t_{k}
つまり、
\frac{\partial L}{\partial \boldsymbol{x}} = \boldsymbol{y} - \boldsymbol{t}
と表せる。
確率的勾配降下法
SGD(Stochastic Gradient Descent)ともいう。
ランダムに選ばれたサンプルに対して順伝播と逆伝播を実行して、パラメータの更新を行う。