記事の概要
ここでは,論文Deep Self-Learning From Noisy Labels[1]を紹介します.この論文はICCV2019にて採択されているものです.また,Pytorchによる実装をGitHubで公開しています.ただ,精度はそれほど出ておらず,この原因の考察はこの記事の最後に述べています.
論文の内容
概要
本論文で取り組んでいるのは,深層学習による画像クラス分類のタスクにおける,ノイズの含まれるデータセットを用いた学習の精度の向上です.ここでの「ノイズを含む」というのは,データセットのクラスラベルが誤って付加されているという状況を示すものです.深層学習ではモデルの学習のために一般に大きなデータセットが必要とされますが,ラベルの整備された巨大なデータセットを準備するのはかなり面倒です.加えて,厳密なデータセットを作るときには人間が手動でアノテーションを行うのが一般的ですが,その際にミスが起こることも考えられます.一方で,Webからクローリングしてきたデータをそのまま用いれば簡便にラベル付き巨大データセットを揃えることができますが,この場合には一般により多くのラベルのミスが含まれています.このような現状から,ある程度ノイズを含んだデータセットを用いて正しく学習を行える深層学習モデルは現実世界において有用だと考えられ,本論文はその実現を目指すための論文になります.
本論文の新規性
ノイズの含まれるデータセットを用いた深層学習の既存の研究は多くあります.そのなかには,ラベルの誤り率を示すための遷移行列を導入したり,ノイズに強い損失関数を設定したりというものがあります.しかしそれらの手法では,ラベルの間違いがランダムであるという仮定を暗黙のうちに置いています.一方で現実的には,ラベルのノイズは入力に依存することが多くあります.例えばどのクラスに属するか紛らわしい画像では,誤ったラベルがつけられる可能性が高くなります.本論文では,そのような現実世界におけるラベルのノイズに即した学習を提案しています.
また,もう一つのこの論文の特長として,ノイズのないデータセットなどの付加情報を用いる必要がないということが挙げられます.既存の研究では,手動でノイズを除いたデータセットを用いている手法も多くあります.しかし既に述べたように手動でのラベル付加は限られた数であっても負担となります.本手法では,ノイズの含まれたデータセットのみを用いて,いわゆるself-learningの形式でモデルの学習を行っています.
手法の概要
提案手法のモデルの学習では,学習フェーズとラベル訂正フェーズという二つのフェーズが存在します.これらのフェーズは,1エポックごとに交互に行われます.
学習フェーズ
学習フェーズでは,画像分類のためのモデルFを学習させます.このフェーズは,一般的に行われる深層学習のトレーニングとほとんど同じだと思ってください.ただ一点だけ,損失関数が少し異なり,下の式の$L_{TOTAL}$のように表されます.
$$
L_{TOTAL} = (1 - \alpha) L_{CCE}(F(\theta, x), y) + \alpha L_{CCE}(F(\theta, x), \hat{y})
$$
ここで,$L_{CCE}$はクロスエントロピー損失関数です.また,$y$はデータに付けられたラベル,$\hat{y}$は訂正されたラベルです.この$\hat{y}$は,後で説明するラベル訂正フェーズで得るものです.$\alpha$はハイパーパラメータで,この二つの損失関数のバランスをとるためのものです.なお,最初のエポックではラベル訂正フェーズはまだ行われておらず訂正ラベルは得られないので,$\alpha = 0$とします.
ラベル訂正フェーズ
続いてラベル訂正フェーズについて説明します.このフェーズの目標は,上手く訂正したラベル$\hat{y}$を手に入れて,学習フェーズで使えるようにすることです.また,そのために,以下のステップを踏みます.
- 各クラスの訓練データからランダムにそれぞれ$m$個のサンプルをとる.
- 各クラスの$m$個のサンプルから代表となるプロトタイプ$p$個を決める.
- 全部のデータに対して各クラスのプロトタイプとの類似度から訂正ラベルを決定する.
順番に説明していく前に,ここで用いるデータごとの「類似度」について定義しておきます.まず,深層学習モデル$F$を,$F = f \circ G$と定義します.ここで,$G$は特徴量抽出層,$f$は分類のための全結合層です.これを用いて,入力$x_1$,$x_2$に対して,類似度を$G(x_1)$と$G(x_2)$のコサイン類似度とします.すなわち,
$$
\frac{G(x_1)^\mathsf{T}G(x_2)}{||G(x_1)|| ~ ||G(x_2)||}
$$
のように表します.以下では「類似度」という記述はすべてこの「特徴量ベクトルのコサイン類似度」と捉えてください.
サンプリング
まず各クラスから$m$個のデータをランダムにサンプリングします.これは,以降の計算にデータ数$n$に対して$O(n^2)$の計算量がかかるので,それを削減するためのものです.
プロトタイプの決定
続いて各クラスごとに,先ほど選んだ$m$個のデータのなかから$p$個のプロトタイプを決定します.このプロトタイプに求める条件は,各クラスの特徴量を上手く表してくれているということです.より具体的には,以下の二つの条件を上手く備えたものをプロトタイプとします.
・自身と似ている特徴量が多く存在する.
・他のプロトタイプとはなるべく似ていない.
つまり理想的には,クラス内の特徴量に$p$個のクラスタがあれば,$p$個のプロトタイプがそれぞれのクラスタ内の代表点としたいわけです.以下に具体的な手法を書きます.
第一に,$m$個の特徴量の類似度を調べます.行列$S$を,$S_{ij}$が$i$番目のサンプルと$j$番目のサンプルの類似度となるように定義します.
第二に,各サンプルの密度$\rho$を定義します.これは,そのサンプルの周りにどれくらい点が密集しているかを示しています.
$$
\rho_i = \sum_{j = 1}^m sign(S_{ij} - S_c).
$$
ここで,$sign$は,正の値に対して$1$を,負の値に対して$-1$を,$0$に対して$0$を返す関数です,また,$S_c$は適当な基準値で,ここでは$S$の中で上位40%に当たる数値としています.これにより,自分と似ているサンプルの数が多いものほど$\rho$の値も大きくなります.
第三に,各サンプルのプロトタイプ決定用の類似度$\eta$を定義します.
\eta_i = \max_{j, \rho_j > \rho_i} S_{ij} ~~(\rho_i < \rho_{max}), \\
\eta_i = \min_{j} S_{ij} ~~(\rho_i = \rho_{max})
すなわち,密度$\rho$が最大のものはなるべく小さい類似度をとり,それ以外のものは,自分より密度$\rho$が大きいサンプルの中から最大の類似度をとります.これにより,$\eta$が小さいものほど,プロトタイプに相応しい性質を兼ね備えていると言えることになります.
そして最後に,$\rho$と$\eta$を用いてプロトタイプの決定を行います.$\rho$は小さい方が良く,$\eta$は小さい方がいいことに留意してください.ここでは,$\eta < 0.95$を満たす中から$\rho$が大きい上位$p$個のサンプルを取得します.これをそのクラスのプロトタイプとします.
訂正ラベルの生成
各クラスのプロトタイプが求まったので,すべてのデータについて訂正ラベルを求めます.単純に,プロトタイプ群によく似ているクラスに振り分けるだけです.各データに対して,それぞれのクラスのプロトタイプとの類似度の平均を算出し,その値が最も大きかったクラスのラベルを訂正ラベル$\hat{y}$とします.
論文の実装
ここからは論文の実装について記していきます.ソースコードはGitHubを確認してください.ただし,既に書いたように論文で記されている精度は確認されていません.この原因の考察は最後に記します.
実装概要
論文と同様に,Clothing1M[2]データセットとFoodLog-101N[3]データセットを用いて実験を行いました.また,FoodLog-101NデータセットはFoodLog-101[4]データセットをテストデータに用いることを想定されているようなので,それに従います.モデルやハイパーパラメータなども論文中に書かれている内容をそのまま用いています.
主な実行環境の詳細を記しておきます.
・Python : 3.5.2
・CUDA : 10.2
・Pytorch : 0.4.1
・torchvision : 0.2.1
・Numpy : 1.17.2
結果
論文中に書かれているAccuracyは下の表のようになっています.CCEは単純にクロスエントロピーを用いて最適化を行ったときの精度です.
| CCE | 提案手法 | |
|---|---|---|
| Clothing1M | 69.54 | 74.45 |
| Food-101N | 84.51 | 85.11 |
一方で,再現実装におけるAccuracyは下の表のようになっています.提案手法の精度で曖昧な雰囲気にしているのは,かなり乱数による誤差が大きかったためです.後に述べますが,この原因について様々な確認をしていたこともあり,このブレの程度に関する定量的な評価はできていません.ただ,提案手法がCCEを有意に超えるような現象は見受けられません.
| CCE | 提案手法 | |
|---|---|---|
| Clothing1M | 68.10 | 64前後 |
| Food-101N | 85.05 | 80前後 |
精度低下の考えられる原因
実装が間違っている可能性
ここは本実装が間違っていない保証をただ述べる項ですので,興味のない方は読み飛ばしてください.
本実装に間違いがあるとした場合,クロスエントロピーを用いたときの精度は論文とそこまで変わらないので,問題があるのはラベル訂正に関わる部分かと思います.これを,訂正ラベルを生成する部分,訂正ラベルを利用する部分の二つに切り分けて確認しています.
第一に,訂正ラベルを生成する部分の確認についてです.まず,そこに関係ある関数は想定通りの挙動をしていることを個別に確認しました.次に,訂正後ラベルと元のノイジーラベルはある程度一致しており,ある程度ノイジーラベルに沿ったラベル訂正が行われていることも確認しています.さらに,ラベル訂正の挙動の正確性についての定量的な確認も行いました.Clothing1Mについては,データセットの一部にクリーンなラベルが付けられているので,ラベル訂正の精度を確認することができます.ここではラベル訂正の精度にスポットを当てるため,学習済みモデルと訓練データにより生成したラベル訂正モジュールを用いてテストデータにラベルを振り,訓練データ全体のラベルの正解率と訂正後のテストラベルの正解率を比較しました.このときの結果は下の表のようになっています(論文中では訓練データのラベル正解率が61.74となっていますが,Clothing1Mの元論文では61.54となっているため,そちらを信用します).これを見ると,元の訓練データのノイズを含むラベルのAccuracyは上回っていることは分かります.
| 訓練データのラベル | テストデータの訂正ラベル |
|---|---|
| 61.54 | 69.92 |
このようなことから分かる通り,全体としてのラベル訂正の挙動は合っていると考えられます.以上によりラベル訂正モジュールは正しいことが確認できるかと思います.
第二に,訂正ラベルを利用する部分の確認です.これについては,ソースコードの訂正後のラベルを受け渡す箇所を,訂正前のラベルを受け渡すように書き換えた上で実験したところ,元のCCEと同程度の精度が出ました.したがって,訂正ラベルを用いた最適化を行う部分にも間違いはないと考えられます.以上二つの理由から,実装バグの観点はクリアしていると考えています.
実行環境の違い
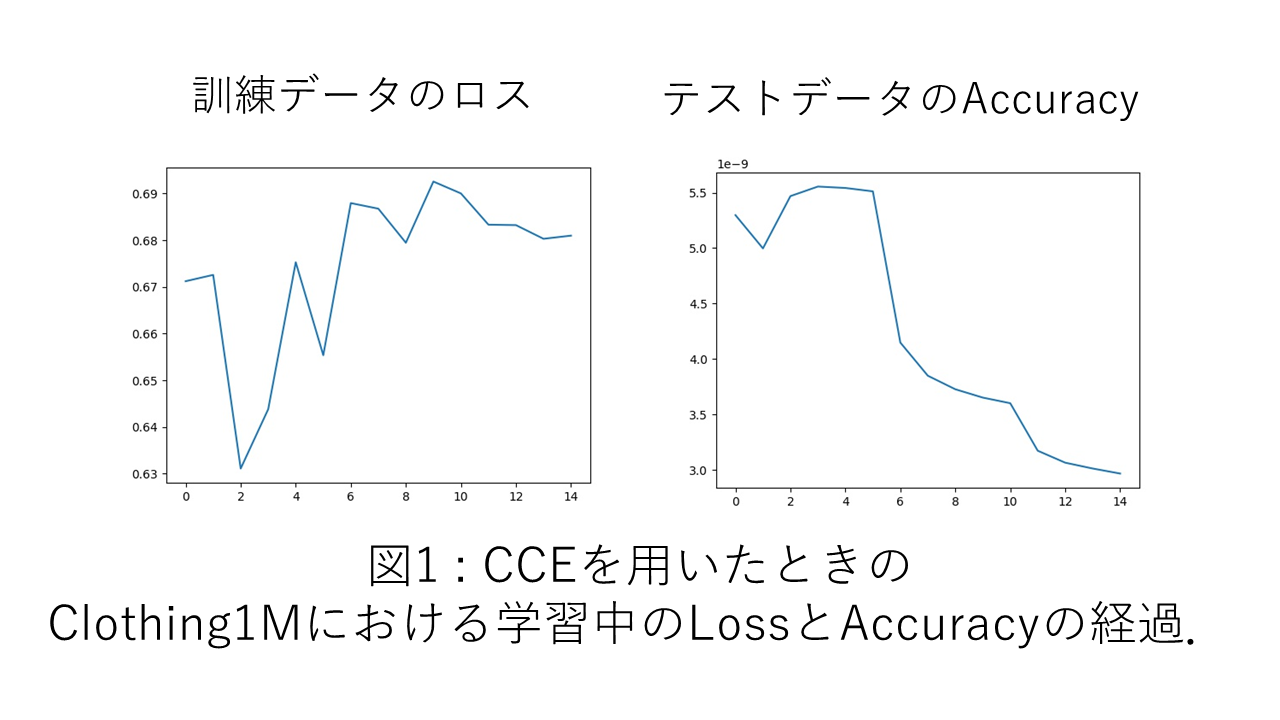
今回用いたハイパーパラメータは,論文中のものをそのまま用いており,例えばClothing1Mでは計15エポックで5エポックごとに学習率を減衰させています.しかし図1を見ると分かるように,最初の5エポックは学習率が大きすぎて不要なようにも見えます.このようなことが起こる原因として,一つ大きく考えられるのは,実行時に用いたライブラリやバージョンの違いかと思います.
ラベル訂正フェーズを開始するタイミングについて
ラベル訂正フェーズは,ニューラルネットワークがある程度適切な特徴量を抽出できるようになってからでないと,逆に精度を悪くする可能性があると考えられます.元論文でも最初はラベル訂正フェーズを挿入しないことを暗に示すような記述があるのですが,その具体的な設定については述べられていません.本実装においては,1エポック目終了直後からラベル訂正フェーズを始めたときの結果を示しています.論文を読む限り1エポック目終了後からラベル訂正が始まるようにも見えるのですが,完全にそうではないと言い切れないような書き方がされているようにも思われます.
実際に実験してみると,最初の方のエポックでラベル訂正を入れたことによりAccuracyが序盤で30%付近まで落ちる現象も場合によっては確認されました.そこで,ラベル訂正フェーズを開始するエポックをいくつか変えたところ,Accuracyがガクリと下がる現象は消えても,最終的な精度はそこまで変わりませんでした.より長いエポック数で途中からラベル訂正を入れるようにすれば結果は変わるかもしれませんが,これについては疑問が残るままです.
乱数
結果の分散の定量的な評価はできていないのですが,学習の波の激しさや数回試した雰囲気から,乱数の影響は無視できないかと思います.元論文についても,少なくともFood-101Nについては,この手法による精度の向上は乱数による影響の範囲を抜け出していないように感じます.ちなみに,Food-101Nの実験に関しては元論文もそこまで詳しく解析していません.
おまけの考察
Food-101Nにおいては元論文でもそこまで精度の向上が見られず,乱数で説明がついてしまう可能性についても述べましたが,この原因は手法そのものにあるかと思います.14クラスの分類であるClothing1Mは訂正ラベルは十分高い確率で元ラベルと同じラベルとなっていますが,101クラスの分類であるFood-101Nでは,訂正ラベルが元ラベルと同じラベルになる確率はClothing1Mに比べて全体的に低いことが確認されました.Food-101Nはクリーンなラベルがついていないので訂正ラベルの正確性は分かりませんが,Clothing1Mよりは低い値になっていることはほぼ間違いないと思います.そして,101クラスの分類を少数のプロトタイプを用いて行うことの難しさを考えれば,不思議ではない結果であるように思います.そのためFood-101Nのような多クラスでの分類の場合にこの手法を適用する場合には,決定的にクラスを割り振らないようソフトラベルを用いたり,訂正ラベルを用いた学習の重みを減らしたりする工夫が必要になってくるかと思います.
参考文献
[1] Jiangfan Han, Ping Luo, and Xiaogang Wang. Deep Self-Learning From Noisy Labels. In International Conference on Computer Vision, 2019.
[2] Tong Xiao, Tian Xia, Yi Yang, Chang Huang, and Xiaogang Wang. Learning from Massive Noisy Labeled Data for Image Classification. In Computer Vision and Pattern Recognition, 2015.
[3] Kuang-Huei Lee, Xiaodong He, Lei Zhang, and Linjun Yang. CleanNet: Transfer Learning for Scalable Image Classifier Training with Label Noise. In Computer Vision and Pattern Recognition, 2018.
[4] Lukas Bossard, Matthieu Guillaumin, and Luc Van Gool. Food-101 – Mining Discriminative Components with Random Forests. In European Conference on Computer Vision, 2014.