私のブログからの転載です。プログラミングやソフトウェア周りの記事を書いているのでご興味あればのぞいてみてください。
この記事のまとめ:
- CourseraのDeep Learning講座のコース1: Neural Networks and Deep Learning のWeek 1, 2の要点と、よくわからなかったところを補完のために調べたことなどを備忘録としてまとめています。
背景
機械学習の勉強のために、以前Andrew Ng先生のCoursera Machine Learning講座を受講したわけですが、そのさらに実践・応用編として同じくAndrew Ng先生のDeep Learning講座があり、その中に5つのコースがあります。以前から興味があったのですがなんだかんだで時間は空いたもののまずはコース1のNeural Networks and Deep Learningを受講開始したので、備忘録兼あまり詳細に語られていない部分について文字に起こして理解を深めようと思います。
Week 1とWeek 2の概要
5つあるコースの内、コース1であるNeural Networks and Deep Learningコースは次のような4週構成になっております。本記事ではWeek 1の前提的な話はあまりせず、Week 2のロジスティック回帰について主に整理します。
- Week 1:Deep Learningの前提的な話
- Week 2:ロジスティック回帰、使用する数式表現、Pythonの使い方
- Week 3:隠れ層の少ないニューラルネットワーク、活性化関数、ランダム初期化
- Week 4:隠れ層が多いニューラルネットワーク(=Deep Learning)
ニューラルネットワークの数式表記表
特徴ベクトル$x$ とラベル$y$ からなる教師セットを$(x,y)$ と示し、$x$ は$n_{x}$ 次元の情報で、$x \in \textbf{R}^{n_{x}}$ ($n_{x}$ 次元実数空間) と表せます。ラベル$y$ は、例えば二項分類問題 (Binary Classification)のケースでは$0$ もしくは$1$ のみをとり、$y={0,1}$ と表せます。教師セットが$m$ 個あるとき、教師データは ${(x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}), ... , (x^{(m)},y^{(m)})}$ のように表せます。
また、特徴ベクトル$x$ とラベル$y$ をそれぞれコンパクトに表すために行列で表すこともあります。
$m$ 個の特徴ベクトル$x$ を並べた$X$ を次のように定義します。
X = \left.\left[
\vphantom{\begin{array}{c}1\\1\\1\end{array}}
\smash{\underbrace{
\begin{array}{ccc}
|&|&\cdots &|\\
x^{(1)}&x^{(2)}&\cdots &x^{(m)}\\
|&|&\cdots &|
\end{array}
}_{m \text{ columns}}}
\right]\right\}
\,n_{x}\text{ rows}
$X$ の次元は$X \in \textbf{R}^{n_{x} \times m}$ です。
また、同様に$m$ 個のラベル$y$ を並べた$Y$ を次のように定義します。
Y = \left[ y^{(1)}, y^{(2)}, \cdots, y^{(m)} \right]
$Y$ 次元は$Y \in \bf R \it ^{1 \times m}$ です。
ロジスティック回帰 (Logistic Regression)
ロジスティック回帰は、二項分類問題$y \in {0,1}$ のときに使うアルゴリズムです。予測$\hat{y}$ は
\hat{y} = \text{P} \left( y=1 | x \right)
0 \le \hat{y} \le 1
であり、このとき下記で表される予測を行うものがロジスティック回帰です。
\hat{y} = \sigma \left( z \right) = \frac{1}{1+e^{-z}}
\text{where} \ \ z = w^{T}x+b
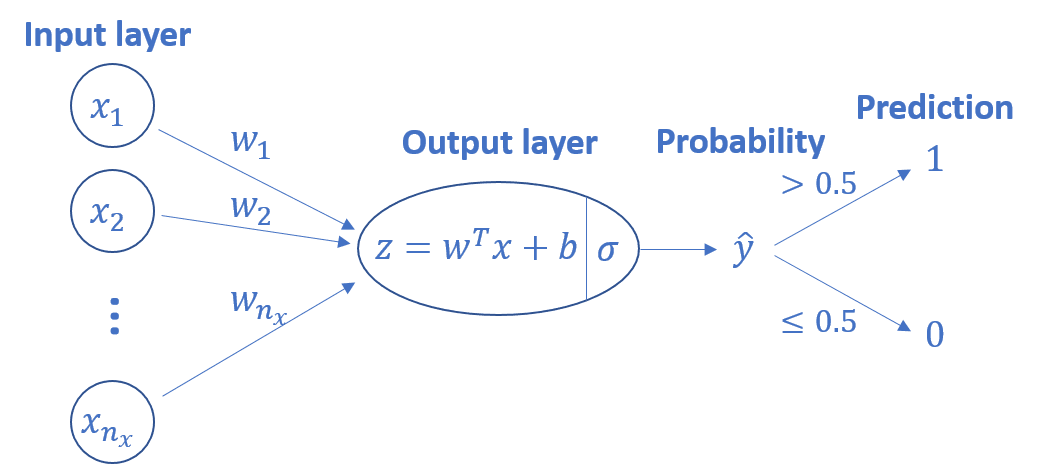
$\sigma \left( z \right)$ はロジスティクス回帰における活性化関数 (Activate Function)であり、シグモイド関数、あるいはロジスティック関数と呼ばれる活性化関数が使われます。$w$ は入力に対するウェイトであり、$b$ はバイアスです。
これらを図で表すと次のように表せます。図のとおり、予測に向かって順に信号を伝えていくことから、予測を計算する手順を順伝搬といいます。
なお以後、予測 $\hat{y}$ は $a$ と表すことがあります。これは、Week 3以降を受講するとわかりますが、ニューラルネットワークでは入力層と出力層の間にいくつかの隠れ層があることがあり、$\hat{y}$ をニューラルネットワークの出力層が出力した結果として予測を表すときにだけ使い、出力層を含むすべて層の出力を $a$ で表現するためです。
ロジスティクス回帰におけるコスト関数と損失関数
ロジスティック回帰による学習を行うということは、教師セットを用いて、最適な$w$ と$b$ を導くことです。そのために、損失関数 (Loss Function)とコスト関数 (Cost Function)を導入します。
損失関数は正しいラベルと予測値との差を表す関数で、損失関数の値が小さいほど予測精度が高いといえます。ロジスティック回帰(二項分類問題)での損失関数は次の通りです。
L (a,y) = - \left( y \ \text{log} \ a + (1-y) \ \text{log} \ (1-a) \right)
また、コスト関数はすべての教師セットの損失関数の平均を表します。コスト関数は次の通り表せます。
J(w,b)=\frac{1}{m} \Sigma_{i=1}^{m} L \left( \hat{y}^{(i)},y^{(i)} \right)
これらの関数の意味は、「Explanation of logistic regression cost function」のビデオを見ましょう。(私が軽くスルーしただけ…)
最適な$w$ と$b$ を導くということはコスト関数$J(w,b)$ が最小となる値を探すことです。ただし、一般的には$w$ の次元が高く、数理計算で求まるものではないため、最適化アルゴリズムを用いて近似解を導出します。
最急降下法 (Gradient Decent)
最急降下法は、連続最適化問題を解くための単純な勾配法のアルゴリズムの一つで、コスト関数の傾き(一階微分)に基づいて関数の最小値を探索します。
勾配法では反復法を用いて極小解を求めます。下記のようにコスト関数の変数である$w$ と$b$ を傾きを基に更新していきます。なお、$\alpha$ は学習レートであり、学習の速さを調整するためのパラメータです。
w := w - \alpha \frac{\partial J(w,b)}{\partial w}
b := b - \alpha \frac{\partial J(w,b)}{\partial b}
ロジスティクス回帰の最急降下法による学習の実装
コスト関数の傾きの計算
活性化関数がシグモイド関数の場合において、ある教師セットにおける損失関数の傾きは下記のように計算できます。
\frac{\partial L(a,y)}{\partial w} = \frac{\partial L(a,y)}{\partial a}
\frac{\partial a}{\partial z} \frac{\partial z}{\partial w} = ( a - y ) x
\frac{\partial L(a,y)}{\partial b} = \frac{\partial L(a,y)}{\partial a} \frac{\partial a}{\partial z} \frac{\partial z}{\partial b} = a - y
なお、それぞれの偏微分は下記の通りです。ここでは偏微分の詳細は省略します。
\frac{\partial L}{\partial a} = - \frac{y}{a} + \frac{1-y}{1-a} \\
\frac{\partial a}{\partial z} = (1-a)a \\
\frac{\partial z}{\partial w} = x \\
\frac{\partial z}{\partial b} = 1
上記で損失関数の傾きを導出できたので、すべての教師セットで平均化すればコスト関数の傾きを導出できます。
これらのコスト関数の傾きを用いて、ウェイト、バイアスを更新することで学習していくのですが、上記の計算とおり、それぞれの順伝搬の過程の逆の手順で勾配計算をする(微分する)ことから誤差逆伝搬法といわれます。これは、Week 4以降の隠れ層が多層になっていくとこの逆伝搬が一般化することができるようになりますのでその際にまた触れていきたいと思います。
ベクトル化
上記では教師セット1つずつに対して損失関数を計算する方法なのですべての教師セットを計算すると$m$ 回のループ処理が必要ですが、コンピューターで計算するうえではループ処理よりも行列演算の方が高速に計算ができますので、すべての教師データに対して一度に計算できるようにベクトル化を行います。するとこれまで表現してきた数式は次のように表せます。
\underbrace{Z}_{1 \times m} = \underbrace{W^{T}}_{1 \times n_{x}} \cdot \underbrace{X}_{n_{x} \times m} + \underbrace{b}_{1 \times 1}
\underbrace{A}_{1 \times m} = \underbrace{\sigma(Z)}_{1 \times m}
\underbrace{\frac{\partial J(W,b)}{\partial W}}_{n_x \times 1} = \frac{1}{m} \underbrace{X}_{n_x \times m} \cdot \underbrace{(A-Y)^{T}}_{m \times 1}
\underbrace{\frac{\partial J(W,b)}{\partial b}}_{1 \times 1} = \frac{1}{m} \Sigma^{m}_{i=1} (a^{(i)} - y^{(i)})
なお、バイアス$b$ については、もともとベクトルでないため総和のループが残ってしまいそうですが、多くのプログラミング言語であれば、総和関数が用意されているのでそれを使用すればループを回避できます。
反復による学習
ここまでできれば、最急降下法で同じ教師セットを繰り返し実行してウェイト$w$ とバイアス$b$ をアップデートすればそれなりに予測精度が得られるようになっていきます。
今回は以上です。 最後まで読んでいただき、ありがとうございます。
つづき
- コース1: Neural Networks and Deep Learning
- コース2: Improving Deep Neural networks