ARIMA、LightGBM、Prophetを使用した時系列解析

はじめに

本記事では以下のサイトを参考に、全4つの時系列ケースでそれぞれのモデルを適応し、時系列予測モデルをつくっています。おそらく参考にしたこの記事の出典はKaggleだと思います。
ARIMA、LightGBM、およびProphetを使用したマルチステップ時系列予測

また、今回sktimeというライブラリを頻繁に用いているために、実装しようとしたら軽く見た方がいいと思います。
sktimeドキュメント

LightGBMに関しての説明は省略されていますが、いずれ記事で投稿したいと思っているので今回は説明の手間を省いてます。

用いるモデル

ARIMA/SARIMAモデル

... 古典的な時系列モデル。時系列データのd階差分系列

y_t - y_{t-d}   

をARIMAモデルで表現。ARIMA(p, d, q)モデルの定義式

y_t - y_{t-d} = c + ϕ_1y_{t-1} + ϕ_2y_{t-2} + ... + ϕ_py_{t-p} + ε_t +θ_1ε_{t-1}+ ... + θ_qε_{t-q}

y_t - y_{t-d} = c + ε_t + \sum_{i=1}^{p}φ_iy_{t-i} + \sum_{i=1}^{q}θ_iε_{t-i}\\
ε_t ... 誤差項、平均0、分散σ^2のホワイトノイズ\\
φ_i, θ_i... モデルのパラメータ\\
c...　定数項

で定義されます。ARIMA(p, d, q)モデルの３つの変数p, d, qはそれぞれp次ARモデル、d階差分系列、q次MAモデルを表しています。

ARモデル(自己回帰モデル) ... ある時点のデータはそれ以前のデータで推定できる。

y_t = c + ε_t  +  \sum_{i=1}^{n}φ_iy_{t-i} + ε_t\\

MAモデル(移動平均モデル) ... 時系列上の各データは過去の誤差に影響される。

y_t = θ_0 + ε_t + \sum_{i=1}^{n}θ_iε_{t- i}

SARIMAモデル ... 季節性を考慮したARIMAモデル。
※後日モデル式はみておきます

Prophet ... Facebookによって開発された新しい静的時系列モデル

y_t = g_t +s_t + h_t + εt\\

g_t ...トレンド関数\\
s_t ...季節変化\\
h_t ...休日効果\\
εt ... 誤差項\\

__$g_t$__は主に2種類あって
1.ロジスティック非線形トレンド

g_t = \frac{C(t)}{1 + exp(-(k+ a_t^Tδ)(t-(m + a_t^Tγ))}\\
C(t)...時間変化すると捉えられた収容上限\\
k + a_t^Tδ...時間変化すると捉えられた成長率\\
m + a_t^Tγ...時間変化すると捉えられたオフセット項

ベースと
2.線形トレンドベース

g_t = (k + a_t^Tδ)t + (m + a_t^Tγ)\\

があります。

__$s_t$__は季節による変動→周期性→信号処理として表現という発想から一般的なフーリエ級数で表現

s(t) = \sum_{n=1}^{N}(a_n\cos(\frac{2πnt}{P}) + b_n\sin(\frac{2nπt}{P}))\\
P...周期

__$h_t$__は分析者自身がイベントカレンダーのリストを作ってモデルに組み込めるように設計。イベントに該当するか否かを0と1で表現し、これに各イベントの係数パラメータベクトルを掛けることで表現。

h(t) = Z(t)k\\
Z(t)...各時点tがD_iに該当するかどうか\\
k...係数パラメータのベクトル

詳細 Prophetのモデル式を1から理解する

LightGBM

米マイクロソフト社が2016年にリリースした決定木アルゴリズムに基づいた機械学習フレームワーク。複数の決定木を一つにまとめるアンサンブル学習のブースティングを用いてる。
※説明省略します

他抑えておきたいもの

##拡張Dickey-Fuller test
時系列標本が単位根を持つかどうかの仮説検定。より大きな負の値をとればとるほど、ある有意水準の下で単位根が存在する仮説を棄却する可能性が高くなる。帰無仮説は系列が非定常で、p値が低いときに棄却されます。

単位根

現系列が非定常過程であり、差分系列が定常過程となる系列の事。具体的にはARIMAモデルやSARIMAモデルの特性方程式の複数個の根が1で一致しているときにこの確率過程が単位根を持つというそうです。なぜ、Dickey-Fuller testを行うかというと、単位根過程に従う時系列データの回帰分析を行うと、まったく関係のない$x_t, y_t$に有意な相関を見出してしまうためです。例えばランダムウォークでは以下のような式で表されます。

y_t = δ + y_{t-1} + ε_t \\
E[ε_t] = 0, V[ε_t] = σ^2

もし系列が単位根過程ならば、正の変化も負の変化も現在のレベルに依存しない確率で行われ、そうでないならば(=系列$y_t$が(トレンド)定常過程)ならば大きな値の後には小さな値(負の変化)が来る傾向があって、小さな値の後には大きな値(正の変化)が来る傾向がある...という感じになります。

自己相関

自己相関関数(ACF, autocorrelation function)とは、時系列上の異なる点での相関を表してます。定常過程{y_t}のラグhの自己相関は

R(t, s) = \frac{E[(X_t-h)(X_s-h)]}{σ^2}

となります。過去の値が現在どのくらい影響しているかを示しており、ズラしたデータのステップ数をラグと呼びます。

偏自己相関

自己相関では現在の時系列&y_t&とラグh離れた$y_{t-h}$だけを参照して相関を求めていましたが、偏自己相関ではラグhまでに含まれる系h-1個の自己相関も考慮して相関を求めます。定常過程{y_t}のラグの偏自己相関は次の方程式における解$φ_{hh}$になります。

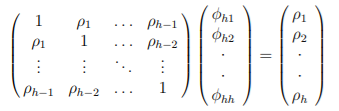
使用する4つの異なる時系列データ

1. 周期的時系列（黒点データ）
2. 傾向と季節性のない時系列（ナイルデータセット）
3. 傾向の強い時系列（WPIデータセット）
4. 傾向と季節性のある時系列（航空会社のデータセット）

どのデータもstatsmodelまたはweb上にあるので別途ファイルを用意する必要はありません。

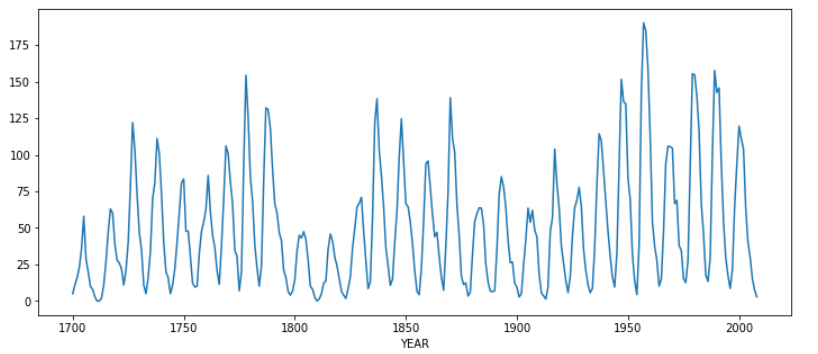
1. 周期的時系列データ(黒点データ)

import statsmodels.api as sm
import matplotlib.pyplot as plt

data = sm.datasets.sunspots.load_pandas()
ts_sun = data.data.set_index('YEAR').SUNACTIVITY
ts_sun.plot(figsize=(12, 5))
plt.show()

statsmodels.api使ったことないのでその説明を交えます
statsmodels.api

data = sm.datasets.sunspots.load_pandas()

statsmodels.api(以下sm)のdatasetsメソッドにデータセットが入っていて、それをpandas形式で取り出しています。とりだしたものはDatasetオブジェクトなので、メソッドを用いてデータセットに含まれるデータを取り出します。
以下Datasetオブジェクトにあるメソッドで呼び出した例

endog...従属変数(目的変数)
exog...独立変数(説明変数) (今回のデータではexog_dataともに使えなかったです)

データのプロット

# 拡張ディッキー・フラー単体テスト、自己相関(ACF)および偏自己相関(PACF)プロットを表示autocorrelation function
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")

def tsplot(y, lags = None, figsize=(12, 7)):
    if not isinstance(y, pd.Series):   # ①
        y = pd.Series(y)
    
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    # 一つの描画キャンパスを複数の領域に分割して、それぞれのサブ領域にグラフを作成
    ts_ax = plt.subplot2grid(layout, (0, 0), colspan=2)
    acf_ax = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    
    y.plot(ax=ts_ax)
    p_value = sm.tsa.stattools.adfuller(y)[1]  # ②
    ts_ax.set_title('Time Series Analysis Plots\n Dickey-Fuller: p={0:.5f}'.format(p_value))
    sm.graphics.tsa.plot_acf(y, lags=lags, ax=acf_ax)
    sm.graphics.tsa.plot_pacf(y, lags=lags, ax=pacf_ax)
    plt.tight_layout()

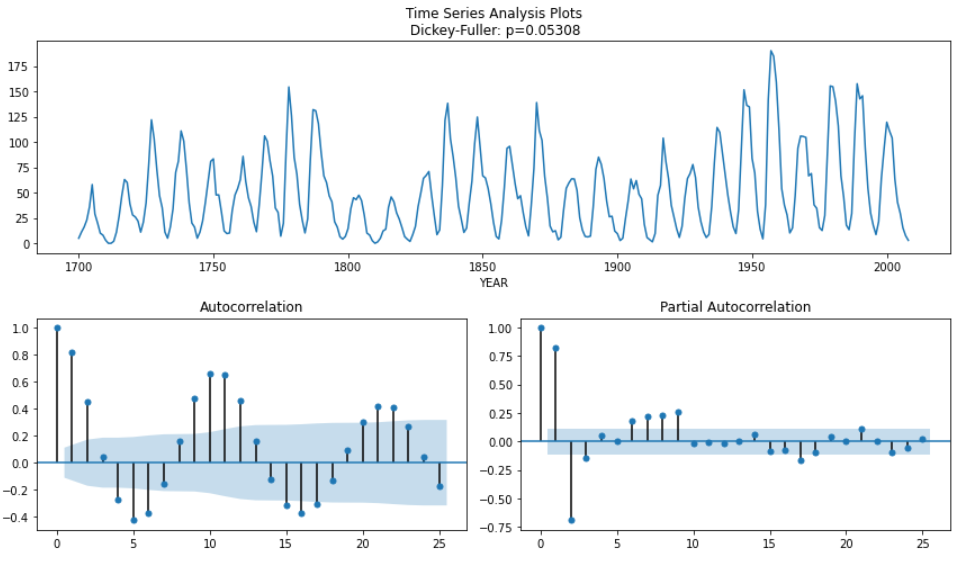
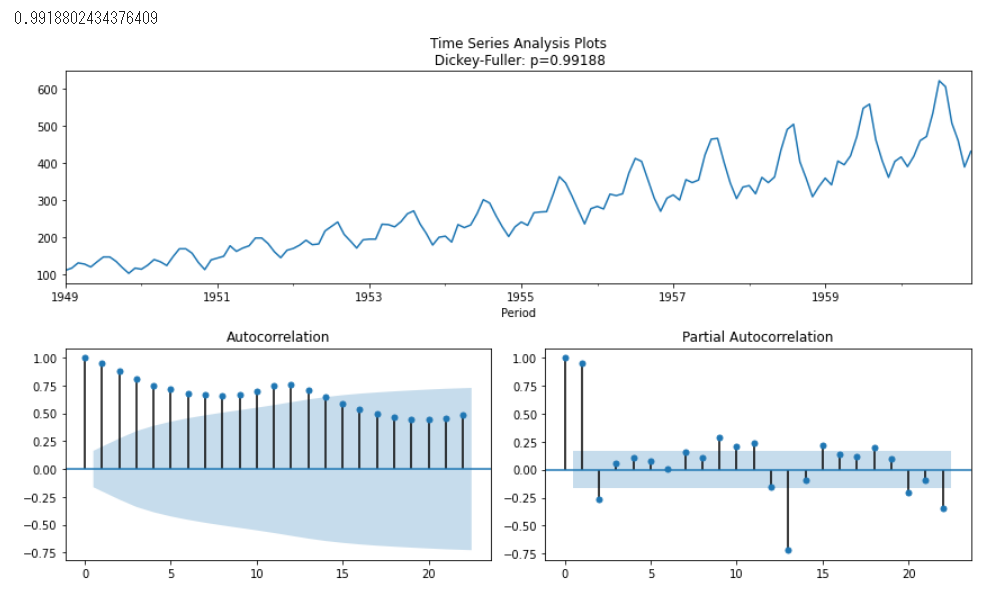
tsplot(ts_sun)

　①のisinstance関数は第一引数にオブジェクト、第二引数に型、返り値にbool型をとり、第一引数がオブジェクトとして第二引数の型、もしくはクラスのインスタンスの時にTrueを返す。
　②sm.tsa.stattools.adfullerの返り値は全部で7つあって、順にadf(テスト統計), pvalue(MacKinnonに基づくおおよそのp値), usedlag(使用されたラグの数), nobs(ADF回帰および臨界値の計算に使用される観測数), 臨界値(1%, 5%, 10%のレベルでのMacKinnonに基づく検定統計量の臨界値), icbest(autolagがNoneでない場合の最大化された情報基準, resstore(結果が属性として添付されたダミークラス)となります。今回は系列が定常か非定常かを検定するので、p値を参考にしています。
結果として、p値は0.0より大きく十分に有意ではないので次は一回差分をとったモデルで時系列データの固定項を排除します。(計量経済学に詳しければ詳しく説明できそうなのが力不`足感じます。)

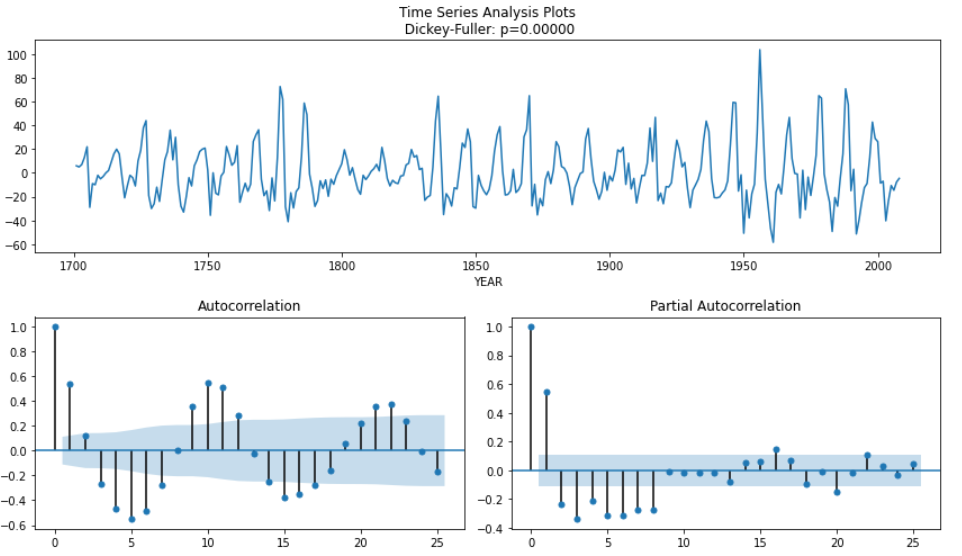
ts_sun_diff = (ts_sun - ts_sun.shift(1)).dropna()
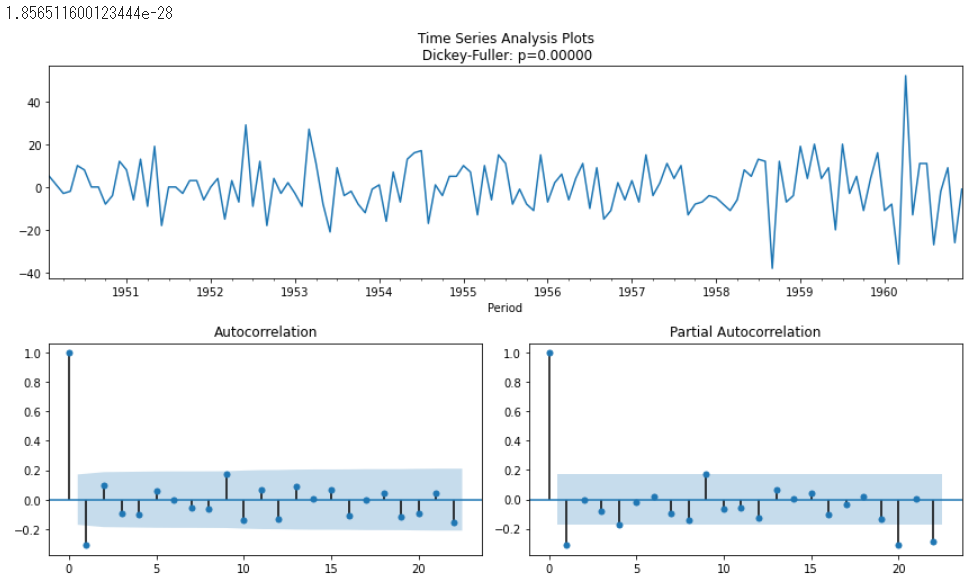
tsplot(ts_sun_diff)

今回はDickey-Fuller検定のp値が有意であり、系列が定常であるとみなせます。実際は系列が定常であるとみなせるまで複数回行います。PACFプロットにはラグ8まで有意な値があるため、ARIMA(8, 1, 0)モデルを意味します(パラメータはそれぞれ自己回帰部分の次数、差分の回数、移動平均部分の次数)。

次のステップでは、ARIMAパラメータの順序を最適化するパッケージのAutoARIMAのsktimeを用います。モデル化する前に、データをトレーニングセットとテストセットに分割してから行
います。

ARIMAモデル

test_len = int(len(ts_sun)*0.2)
sun_train, sun_test = ts_sun.iloc[:-test_len], ts_sun.iloc[-test_len:]

from sktime.forecasting.arima import AutoARIMA  # ③

forecaster = AutoARIMA(start_p = 8, max_p = 9, suppress_warnings=True)
sun_train.index = sun_train.index.astype(int) 
forecaster.fit(sun_train)
forecaster.summary()

③ AutoARIMAの引数は以下になります。
start_p ... p(自己回帰部分の次数)のはじめ
d...階差のはじめ
start_q ... q(移動平均)のはじめ
max_p, d, q...p, d, qの最大
季節性を考慮した場合、d, p, qはそれぞれD, P, Qで指定され、
sp ... 季節性を考慮する期間。4なら四半期データ、12なら月次データ、1なら年次データになります。
seasonal(default=True) ... bool値、季節性を考慮する時、Trueを設定します。
stationary(default=False) ... 時系列が定常ならdは0に設定されます。
suppress_warnings(default=False) ... 警告がたくさん出るので無視したいときにTrueにします。
季節性を考慮したモデルの次数も自動的に決めれるのがポイントです。

モデルのパフォーマンス評価とモデルの予測をプロット

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_absolute_percentage_error


def plot_forecast(series_train, series_test, forecast, forecast_int=None):

    mae = mean_absolute_error(series_test, forecast)
    mape = mean_absolute_percentage_error(series_test, forecast)

    plt.figure(figsize=(12, 6))
    plt.title(f"MAE: {mae:.2f}, MAPE: {mape:.3f}", size=18)
    series_train.plot(label="train", color="b")
    series_test.plot(label="test", color="g")
    forecast.index = series_test.index
    forecast.plot(label="forecast", color="r")
    if forecast_int is not None:
        plt.fill_between(
            series_test.index,
            forecast_int["lower"],
            forecast_int["upper"],
            alpha=0.2,
            color="dimgray",
        )
    plt.legend(prop={"size": 16})
    plt.show()

    return mae, mape

fh = np.arange(test_len) + 1 
forecast, forecast_int = forecaster.predict(fh=fh, return_pred_int=True, alpha=0.05)
sun_arima_mae, sun_arima_mape = plot_forecast(
    sun_train, sun_test, forecast, forecast_int
)

MAE ... 平均絶対誤差

MAE = \sum_{t=1}^{n} \frac{|y_t-\hat{y_t}|} {n} \\

MAPE = \frac{100}{n}\sum_{i=1}^{n} \frac{|y_t-\hat{y_t}|} {y_i}

𝑡は時間、𝑦𝑡は𝑡での実際のy値、𝑦̂𝑡は予測値、𝑛は予測期間
MAEは予測期間中の絶対予測誤差の平均、MAPEは絶対誤差を実際のyで割るMAEのスケーリングされたメトリック。

AutoARIMAでモデル構築されたforecasterはpredict(fh=[1, 2, ...])の形で指定された配列分の予測をだすことができます。

LightGBM

LightGBMで予測を行うには、最初に時系列データを表形式に変換する必要があります。

from sktime.forecasting.compose import make_reduction, TransformedTargetForecaster
from sktime.forecasting.model_selection import ExpandingWindowSplitter, ForecastingGridSearchCV
import lightgbm as lgb

def create_forecaster():
    
    # creating forecaster with LightGBM
    regressor = lgb.LGBMRegressor()
    forecaster = make_reduction(regressor, window_length=5, strategy="recursive")
    
    return forecaster

def grid_serch_forecaster(train, test, forecaster, param_grid):

    # Grid search on window_length
    cv = ExpandingWindowSplitter(initial_window=int(len(train) * 0.7))
    gscv = ForecastingGridSearchCV(
        forecaster, strategy="refit", cv=cv, param_grid=param_grid
    )
    gscv.fit(train)
    print(f"best params: {gscv.best_params_}")
    
    # forecasting
    fh=np.arange(len(test))+1
    y_pred = gscv.predict(fh=fh)
    mae, mape = plot_forecast(train, test, y_pred)

    return mae, mape
    
param_grid = {"window_length": [5, 10, 15, 20, 25, 30]} # parameter set to be grid searched
forecaster = create_forecaster()
sun_lgb_mae, sun_lgb_mape = grid_serch_forecaster(sun_train, sun_test, forecaster, param_grid)

上記例で※が訓練用データ(window_length=5)でxが予測(テスト)用データ(fh=3)で1ステップごとにstep_lenght=1ごとずらしたものになっています。つまり、window_lengthはある値から顧みるデータの個数を示しています。ExpandingWindowSplitterではこのように時系列データを分割しているっぽいです。実際にはForecastingGridSearchCVでparamsにwindow_lengthを指定することでExpandingWindowSplitterのwindow_lengthを最適化しています。

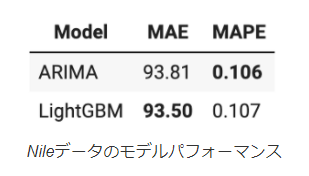
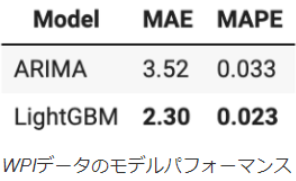
モデルの比較結果

結果として上記図より、LightGBMはARIMAモデルより優れたパフォーマンスを発揮していることになります。この結果を見た時はLightGBMはすごいとと思ったのですが、実際には後述しますが特性上うまく周期性をとれないパターンもあります。

2.傾向と季節性のない時系列（ナイルデータセット）

データのプロット

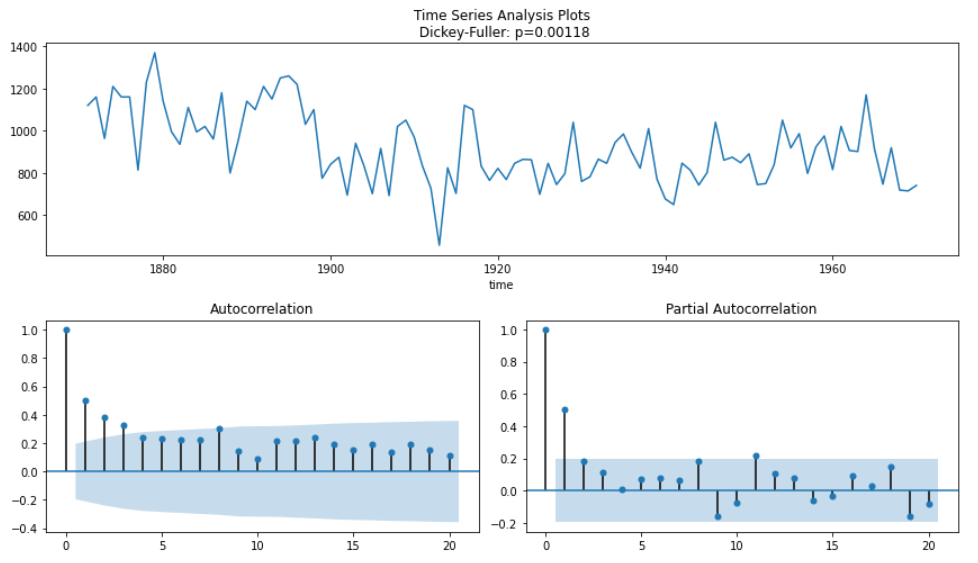
ナイル川のデータセットには、1871年から1970年までの100年間にアシュワンで測定されたナイル川の年間流量の測定値が含まれています。時系列には季節性も明らかな傾向もありません。

ts_nl = sm.datasets.get_rdataset("Nile").data
ts_nl = ts_nl.set_index('time').value

tsplot(ts_nl)

Dickey-Fuller検定から定常であることがわかりますが、ACFプロットにはいくつかの自己相関がみられます。

ts_nl_diff = (ts_nl - ts_nl.shift(1)).dropna()
tsplot(ts_nl_diff)

ACFプロットが即時の低下を示し、Dickey-Fuller検定がより有意なp値を示すため、元のプロットよりも安定した結果がみられます。この結果より、ARIMAモデルのd, pは1が期待されます。

ARIMモデル

test_len = int(len(ts_nl) * 0.3)
nl_train, nl_test = ts_nl.iloc[:-test_len], ts_nl.iloc[-test_len:]

forecaster = AutoARIMA(suppress_warnings=True)
forecaster.fit(nl_train)
forecaster.summary()

モデルはd, p, qそれぞれ1になりました。

fh = np.arange(test_len) + 1
forecast, forecast_int = forecaster.predict(fh=fh, return_pred_int=True, alpha=0.05)
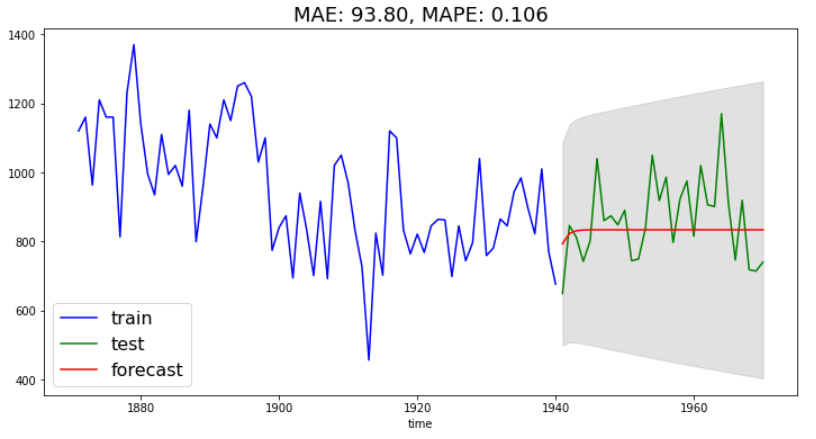
nl_arima_mae, nl_arima_mape = plot_forecast(nl_train, nl_test, forecast, forecast_int)

時系列には明確なパターンがないため、モデルは時間の経過とともにほぼ一定の値を予測している。なんで直線に回帰されたんだろう？とは思いましたが、

LightGBM

param_grid = {"window_length": [5, 10, 15, 20, 25, 30]}
forecaster = create_forecaster()
nl_lgb_mae, nl_lgb_mape = grid_serch_forecaster(nl_train, nl_test, forecaster, param_grid)

こちらのモデルも時間の経過とともにほぼ一定の値を予測してますね。

モデルの比較

結果としてLightGBMとARIMAモデル間には大きな違いがないことを示しています。

3.傾向の強い時系列（WPIデータセット）

1960年から1990年までの米国卸売物価指数（WPI）は、以下に示すように強い傾向があります。

データのプロット

import requests
from io import BytesIO

wpi1 = requests.get("https://www.stata-press.com/data/r12/wpi1.dta").content
data = pd.read_stata(BytesIO(wpi1))
ts_wpi = data.set_index("t").wpi

tsplot(ts_wpi)

stataのデータセットが置いてあるページから直接データを読み込んでいるっぽい？

　データの中身は上記のようになっています。Dickey-Fuller検定より系列が非定常とみなされるので、定常にするためにも一回差分をとります。

'''python
ts_wpi_diff = (ts_wpi - ts_wpi.shift(1)).dropna()
tsplot(ts_wpi_diff)
'''

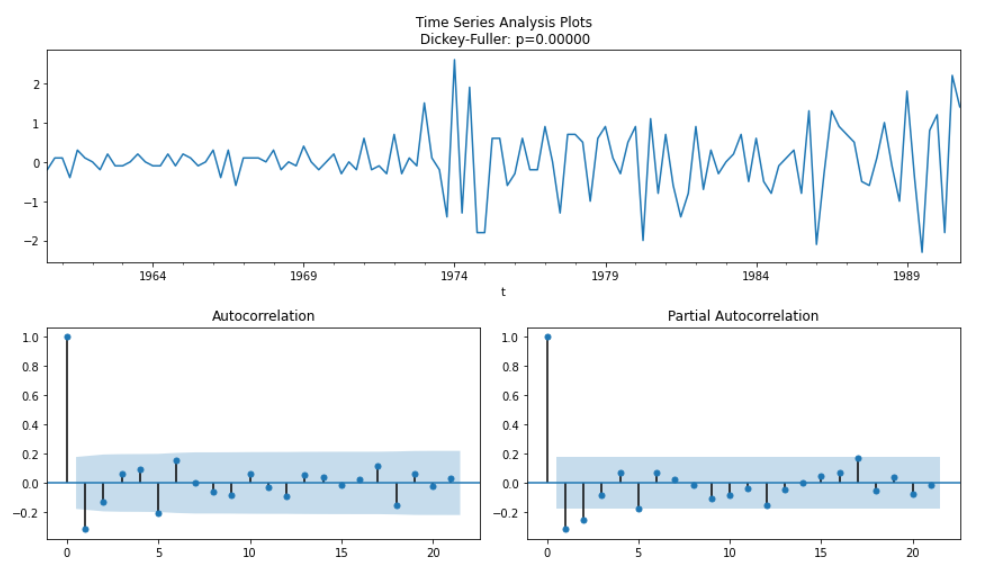
Dickey-Fuller検定より有意な値が得られ、またACFプロットが急激な低下を示しているため、データは安定しているとみなせます。ACDFよりモデルの階差は2を示すのがよいと予測され、ACFはラグ１deyuuinaataiを持ち、PACFはラグ2までの値を持っているため、 p=2、q=1が期待されます。

ARIMAモデル

ts_wpi.index = ts_wpi.index.to_period("Q")
test_len = int(len(ts_wpi) * 0.25)
wpi_train, wpi_test = ts_wpi.iloc[:-test_len], ts_wpi.iloc[-test_len:]

forecaster = AutoARIMA(suppress_warnings=True)
forecaster.fit(wpi_train)
forecaster.summary()

fh = np.arange(test_len) + 1
forecast, forecast_int = forecaster.predict(fh=fh, return_pred_int=True, alpha=0.05)
wpi_arima_mae, wpi_arima_mape = plot_forecast(
    wpi_train, wpi_test, forecast, forecast_int
)

　結果得られたモデルはSARIMAX(0, 2, 1)と階差は違えど他二つ(自己回帰部分の次数、移動平均部分の次数)に関しては正しく得られています。予測部分はナイル川の時とおなじで結局直線の回帰になっています。

LightGBM

param_grid = {"window_length": [5, 10, 15, 20, 25, 30]}
forecaster = create_forecaster()
wpi_lgb_mae, wpi_lgb_mape = grid_serch_forecaster(
    wpi_train, wpi_test, forecaster, param_grid
)

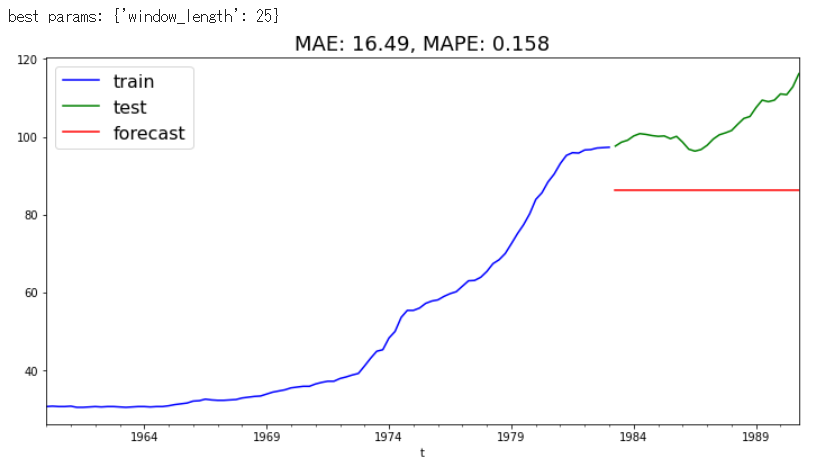
　LightGBMでは明らかにうまく機能していません。原因として、回帰ツリーアルゴリズムはトレーニングデータで見た値を超える値を予測することができないため、時系列に強い傾向がある場合は問題が発生します。一方で時系列が弱い傾向だと黒点データにみられるようにARIMAデータよりよい性能を発揮します。
　しかしながら、モデリングする前にトレンドを除去することで、時系列が弱いデータとして予測することができます。

from sktime.utils.plotting import plot_series
from sktime.forecasting.trend import PolynomialTrendForecaster
from sktime.transformations.series.detrend import Detrender

# linear detrending
forecaster = PolynomialTrendForecaster(degree=1)
transformer = Detrender(forecaster=forecaster)
yt = transformer.fit_transform(wpi_train)

forecaster = PolynomialTrendForecaster(degree=1)
fh_ins = -np.arange(len(wpi_train))  # in-sample forecasting horizon
y_pred = forecaster.fit(wpi_train).predict(fh=fh_ins)

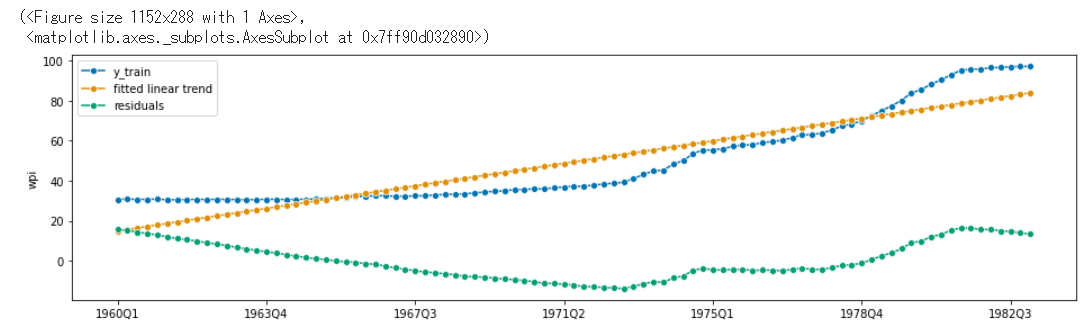
plot_series(
    wpi_train, y_pred, yt, labels=["y_train", "fitted linear trend", "residuals"]
)

PolynomialTrendForecasterはdegreeで指定した次数に合わせて多項式近似を行っています。Detrenderはforecasterで指定した予測子による予測結果と訓練データとの差分を返す関数です。
上記図より、予測したモデル(fitted linear trend)が時系列のトレンドをうまく捕捉していることがわかります。

from sktime.forecasting.compose import TransformedTargetForecaster

def create_forecaster_w_detrender(degree=1):

    # creating forecaster with LightGBM
    regressor = lgb.LGBMRegressor()
    forecaster = TransformedTargetForecaster(
        [
            ("detrend", Detrender(forecaster=PolynomialTrendForecaster(degree=degree))),
            (
                "forecast",
                make_reduction(regressor, window_length=5, strategy="recursive"),
            ),
        ]
    )

    return forecaster


param_grid = {"forecast__window_length": [5, 10, 15, 20, 25, 30]}
forecaster = create_forecaster_w_detrender(degree=1)
wpi_lgb_mae, wpi_lgb_mape = grid_serch_forecaster(
    wpi_train, wpi_test, forecaster, param_grid
)

モデルの比較

4.傾向と季節性のある時系列（航空会社のデータセット）

Box-Jenkins航空会社のデータセットは、1949年から1960年までの国際航空会社の乗客（千単位）の月間合計数で構成されてる。傾向と季節性の両方がある。

データのプロット

from sktime.datasets import load_airline
ts_al = load_airline()

tsplot(ts_al)

Dickey-Fullerが有意な値をとっていないので時系列データを定常にする必要があります。今回は季節性(ラグ12)をとることで静止させます。

ts_al_diff = (ts_al - ts_al.shift(12)).dropna()
tsplot(ts_al_diff)

ACFがゆっくりと低下しているため、まだ静止していないように見えます。そのため、一回差分を追加してみます。

ts_al_2diff = (ts_al_diff - ts_al_diff.shift(1)).dropna()
tsplot(ts_al_2diff)

Dickey-Fullerのp値が有意であり、ACFプロットが時間の経過とともに急速に低下することを示しているため、安定しているように見える。分析結果よりd=1およびD(季節差の次数)=1, p, qのSARIMAが1になる可能性があることを意味する。

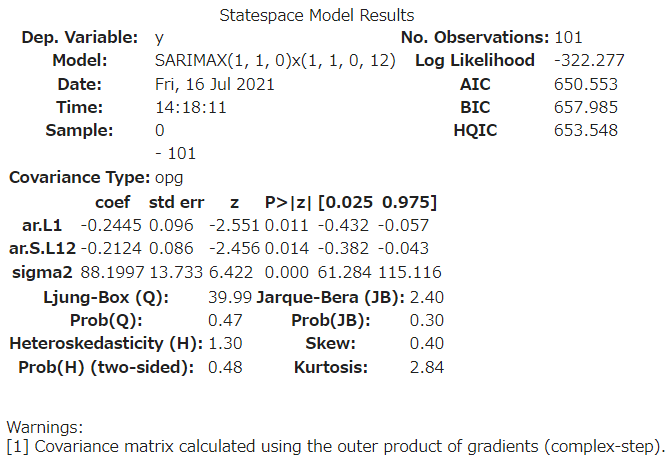
ARIMAモデル

test_len = int(len(ts_al) * 0.3)
al_train, al_test = ts_al.iloc[:-test_len], ts_al.iloc[-test_len:]

forecaster = AutoARIMA(sp=12, suppress_warnings=True)
forecaster.fit(al_train)
forecaster.summary()

予想通り、作成されたモデルはd=1およびD=1になります。

fh = np.arange(test_len) + 1
forecast, forecast_int = forecaster.predict(fh=fh, return_pred_int=True, alpha=0.05)
al_arima_mae, al_arima_mape = plot_forecast(al_train, al_test, forecast, forecast_int)

うまいこと周期性をとらえれているように感じます。

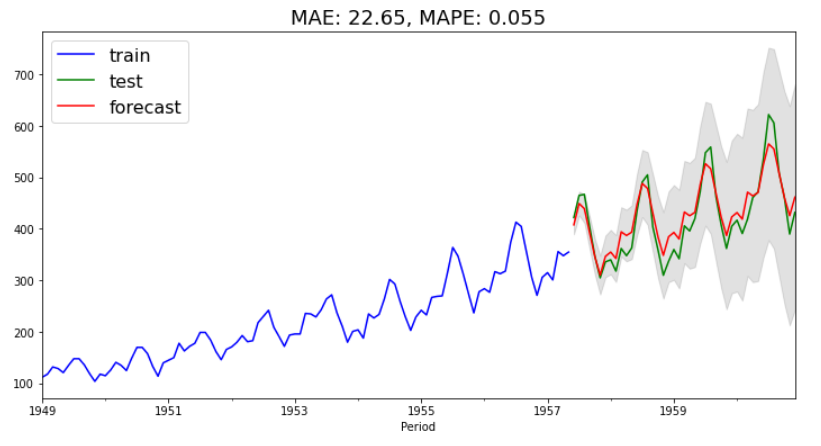
LightGBM

from sktime.transformations.series.detrend import Deseasonalizer

def create_forecaster_w_desesonalizer(sp=12, degree=1):

    # creating forecaster with LightGBM
    regressor = lgb.LGBMRegressor()
    forecaster = TransformedTargetForecaster(
        [
            ("deseasonalize", Deseasonalizer(model="multiplicative", sp=sp)),
            ("detrend", Detrender(forecaster=PolynomialTrendForecaster(degree=degree))),
            (
                "forecast",
                make_reduction(regressor, window_length=12, strategy="recursive"),
            ),
        ]
    )

    return forecaster
    
forecaster = create_forecaster_w_desesonalizer()
param_grid = {"forecast__window_length": [6, 12, 18, 24, 30, 36]}

al_lgb_mae, al_lgb_mape = grid_serch_forecaster(
    al_train, al_test, forecaster, param_grid
)

時系列には季節性があるため、DeseasonalizerでLightGBM予測モジュールを追加しています。季節性の影響は年によって異なるため"multiplicative", Deseasonalizerモジュールを設定している。

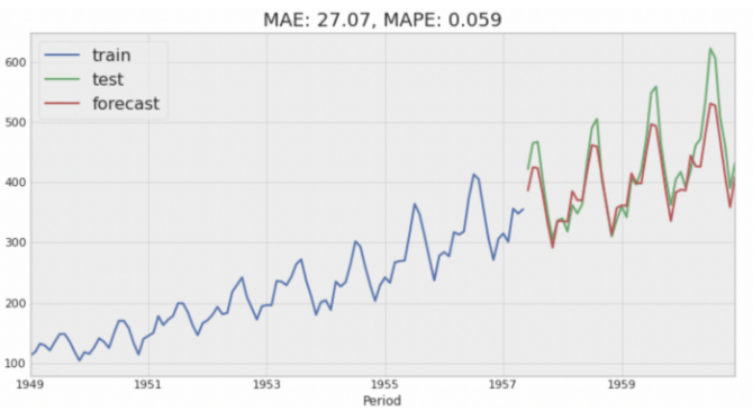
Prohetモデル

　複数の季節性(年次、週次、および日次)に効果的に対処できるモデル。休日の影響を組み込み、時系列にカスタムトレンド変更を実行する機能もある。

from fbprophet import Prophet

al_train_pp = al_train.to_timestamp(freq="M").reset_index()
# Prophet requires specific column names: ds and y
al_train_pp.columns = ["ds", "y"]

# turning on only yearly seasonality as this is monthly data.
# As the seasonality effects varies across years, we need multiplicative seasonality mode
m = Prophet(
    seasonality_mode="multiplicative",
    yearly_seasonality=True,
    weekly_seasonality=False,
    daily_seasonality=False,
)
m.fit(al_train_pp)

future = m.make_future_dataframe(periods=test_len, freq="M")
forecast = m.predict(future)
forecast = forecast.iloc[-test_len:]
forecast.rename(columns={"yhat_lower": "lower", "yhat_upper": "upper"}, inplace=True)
al_pph_mae, al_pph_mape = plot_forecast(
    al_train, al_test, forecast["yhat"], forecast[["lower", "upper"]]
)

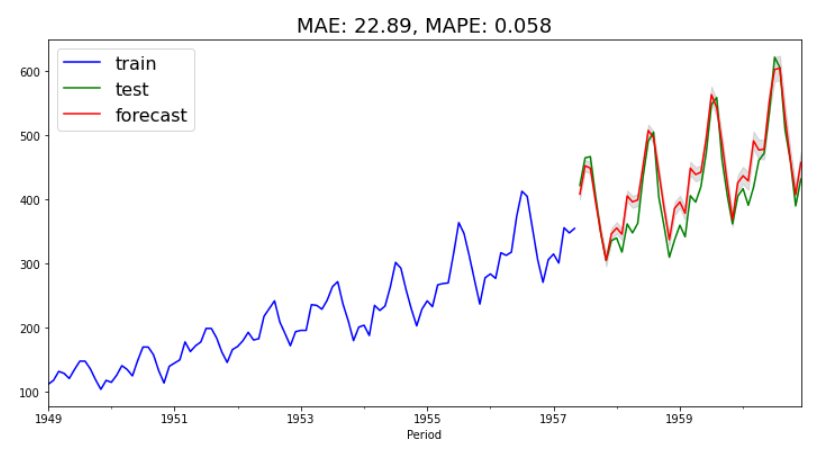
モデルの比較

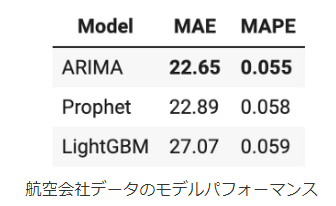
結果としてはARIMAモデルよりもパフォーマンスは落ちましたがかなりいいモデルになっている気がします。

結論

　LightGBMについて、先述の通りモデルの特性上強い傾向のあるモデルに対してはうまく予測ができなかったものの、季節性のない時系列(航空会社以外)ではARIMAと同等またはそれ以上のパフォーマンスを示しました。とはいえ、データに様々な時系列(企業の株価や製品別の売上など)が多数ある場合は単一の機械学習モデルで複数時系列を予測できる可能性があるため、ARIMAモデルやProphetモデルより高い精度が出ています。しかしながら、機械学習アプローチだと予測区間が設定されないので独自にモデルをコーディグする必要があったり、内部で実行されていることがブラックボックス化されているため、線形モデルの方がモデルの解釈性、説明性は高いです。

おわりに

　Kaggleでも今回実装したノートブック以外にも古典的な線形モデルを使った時系列データ解析はあるので今後また参考にして実装したいとおもっています。夏休みは時系列解析、AI関連、計量経済学、統計的因果推論とかそのあたりの記事かいていきたいと思っています。あと、単位根の話が中途半端だったので余力ないですけど余力があれば説明をつけたしたいと思っています。