今回はメタ強化学習についてChelsea Finnによる解説およびUCバークレーのSergey Lavinによる講義(以下URL)を参考にまとめてみたいと思います。
[youtube]
Chelsea Finnによる解説
https://www.youtube.com/watch?v=c0vSwglRY4w&t=1192s
Sergey Lavinの講義
https://www.youtube.com/watch?v=mftNApIM1Yc&list=PL_iWQOsE6TfXxKgI1GgyV1B_Xa0DxE5eH&index=98
[講義スライド]
S. Lavin
https://rail.eecs.berkeley.edu/deeprlcourse/
C. Finn
https://cs330.stanford.edu/
※ 以下の内容でnotationが統一されていない部分がいくつかありますが、ご了承ください
導入
強化学習は囲碁を代表とするゲームやロボットの制御などにおける様々なタスクを解くことができる非常に有力なフレームワークですが、基本的には1から試行錯誤的に学習する必要があるため、通常の強化学習のアルゴリズムでは最適な方策を見つけるまでにかなり時間がかかってしまうという問題点があります。
一方で、人間の場合は例えば初めてプレイするゲームであってもある程度すぐに適応して基本的な操作を習得できることが多いです。これは、人間が過去に他のゲームを習得した経験などを用いることができるからであると考えられます。つまり、人間は「どのように新たなゲームを習得すればよいか」を事前の経験からある程度理解しているため、新たなゲームに対してすぐに適応できると考えられます。
強化学習においてこのような仕組みを取り入れる方法として、今回紹介するメタ強化学習があります。メタ学習・メタ強化学習は一言で表すと、「どのように学習するか」自体を学習するフレームワークです。この点に関しては以降の内容で詳しく触れますが、メタ学習ではあらかじめ複数のタスクにおける経験を用いてモデルを学習することで、学習後に与えられた新たなタスクに対して効率的に学習を行うことができるようになります。
教師ありメタ学習
メタ強化学習の説明に入る前によりシンプルなメタ教師あり学習について見ていきます。ここでは、以下の文献の few-shot learning の例を用いて説明します(図1)。
https://openreview.net/pdf?id=rJY0-Kcll
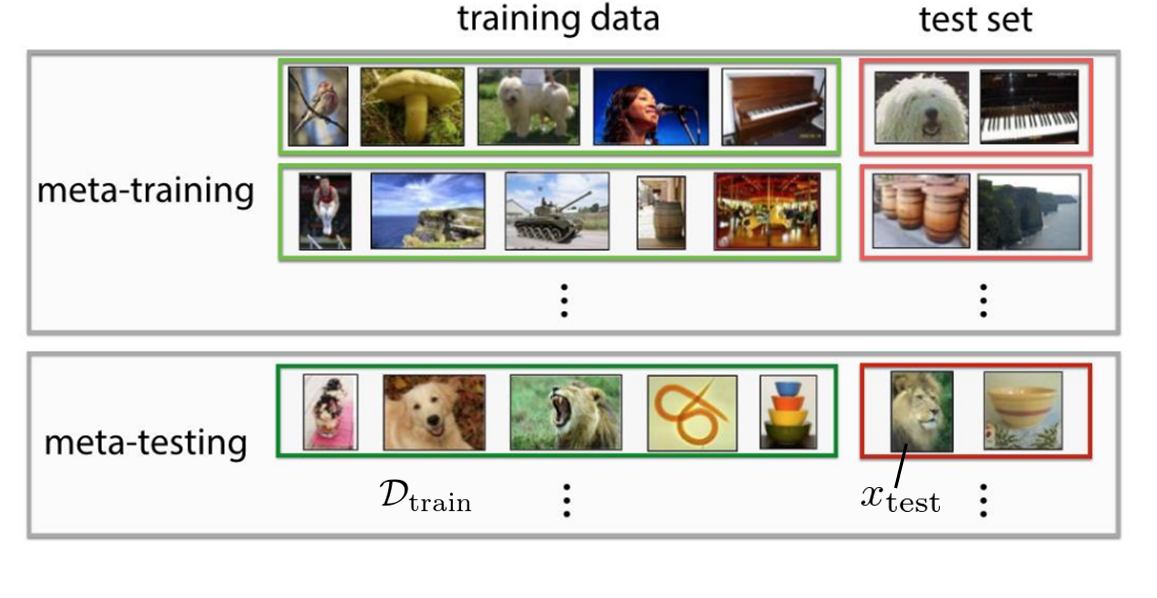
ここでの最終的な目標は図1の下灰色枠内のように、新しく与えられた分類問題(図1の場合は「猫」「犬」「ライオン」「虫」「ボウル」の5つのクラスからなる分類問題)に対して緑枠内のような少量の訓練データ$\mathcal{D}_{\mathrm{train}}$および赤枠内のテスト入力画像$x_{\mathrm{test}}$を入力とし、対応するラベル$y_{\mathrm{test}}$を出力するモデル$y_{\mathrm{test}}=f_{\theta}(\mathcal{D}_{\mathrm{train}},x_{\mathrm{test}})$を学習することです。なお、図1では各クラスに対する訓練データは一つずつしか与えられていません(1-shot learning)が、実際には複数個あっても構いません(few-shot learning)。ただ、通常の教師あり学習のように大量の訓練データを用意するのが困難な場合な場合(例:病気の診断のために用いるCT画像)を想定しており、少量の画像データのみで学習できるのがメタ学習の特徴です。
この例では訓練データが1つしかないので通常の教師あり学習によって正しく分類を行うことができるモデルを学習することは困難ですが、人間から見るとこの分類問題はとても簡単に思えます。これは人間がこれまでの経験を用いることができるからだと考えられます。そこで、メタ学習では、上灰色枠内のように同じ構造を持つ別の分類問題およびその問題に対するデータの組をたくさん用意し、これらを用いてモデル$f_\theta$を学習します(この過程をメタ訓練と呼びます)。メタ訓練が終わると、新たに与えられた分類問題と少量の訓練データ$\mathcal{D}_{\mathrm{test}}$から正しく分類を行うことができるモデル$f_\theta$が得られます。通常の教師あり学習とメタ教師あり学習の違いを改めて以下にまとめます。
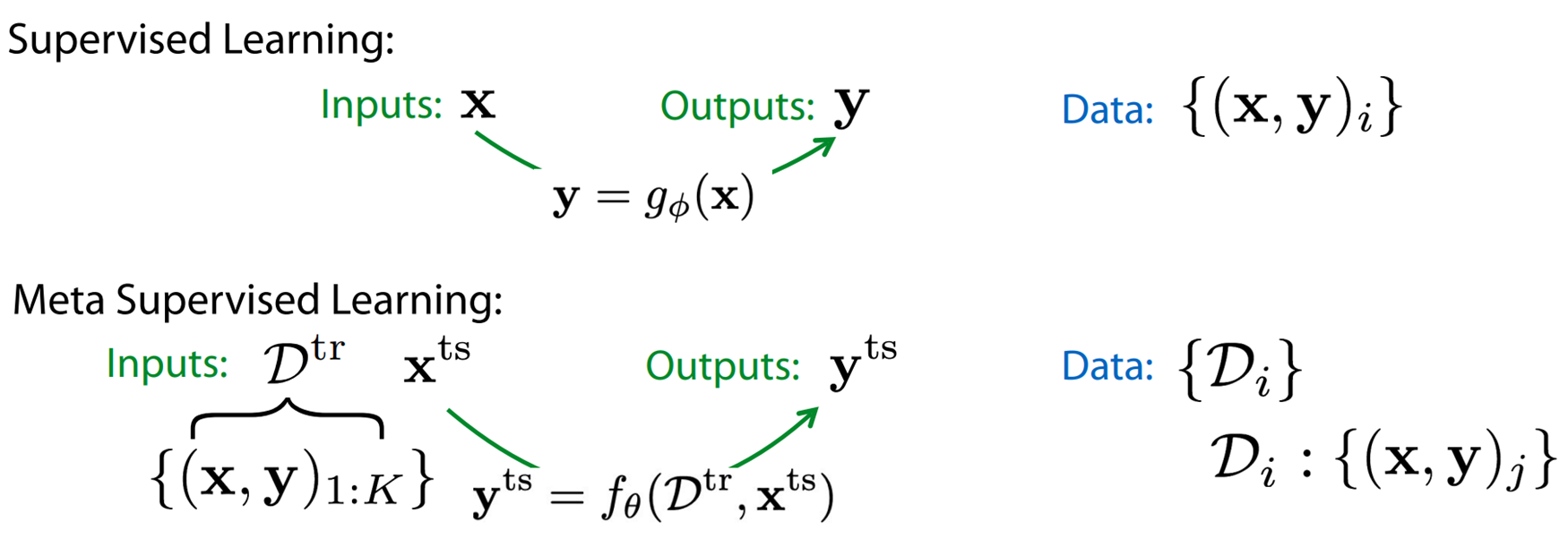
図2. 通常の教師あり学習とメタ学習の比較(C. Finnのスライドより)
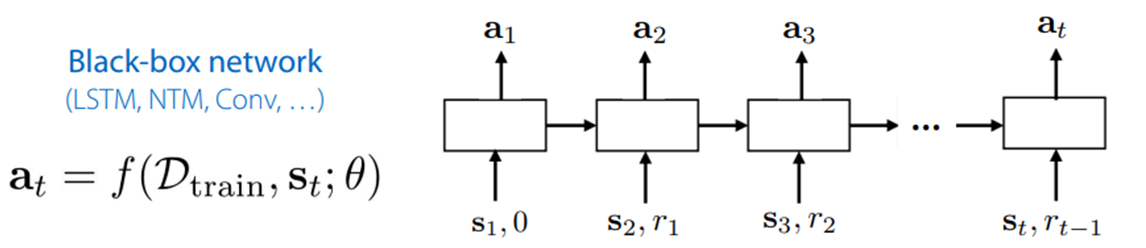
今回は強化学習がメインなので、あまり詳しくは述べませんが、具体的な学習方法について少しだけ触れたい思います。先述の通り、今回学習するのは訓練データとテスト入力を入力とし、対応するラベルを出力とする関数$f_{\theta}$です。従って、通常の教師あり学習とは異なり、訓練データをどのように入力するかを考える必要があります。上記の論文では図3のように、RNNを用いて$D_{\mathrm{train}}$内のデータを順番に入力していき、最後にテスト入力データを入力し対応するラベルを出力する形のモデルを考え、これをメタ訓練データを用いて学習しています。
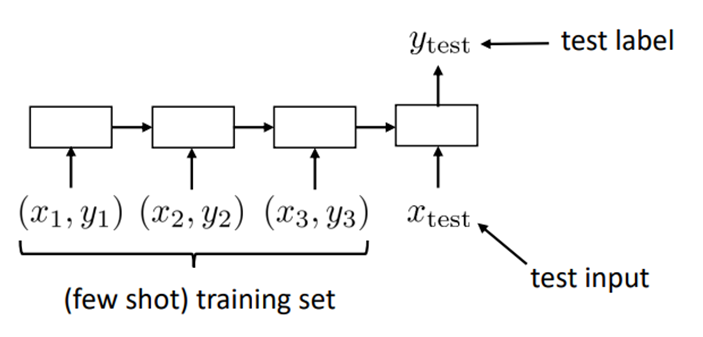
図3. メタ学習でのRNNモデル
メタ強化学習
ここからメタ強化学習の内容に入っていきます。なお、強化学習に関する基本的な説明についてはここでは割愛します。強化学習の基本的な内容については下の記事などを参照ください。
https://qiita.com/icoxfog417/items/242439ecd1a477ece312
メタ強化学習では、メタ教師あり学習の場合と同じように、過去の別のタスク$\mathcal{T}_i\ (i=1,\ldots,N)$での経験を基に、新しく与えられたタスク$\mathcal{T}$に対して出来る限り少ない試行回数で最適な制御方策を学習することを考えます。ここで、タスク$\mathcal{T}$はマルコフ決定過程(MDP)で表され、確率分布$p(\mathcal{T})$に従うものと仮定します。
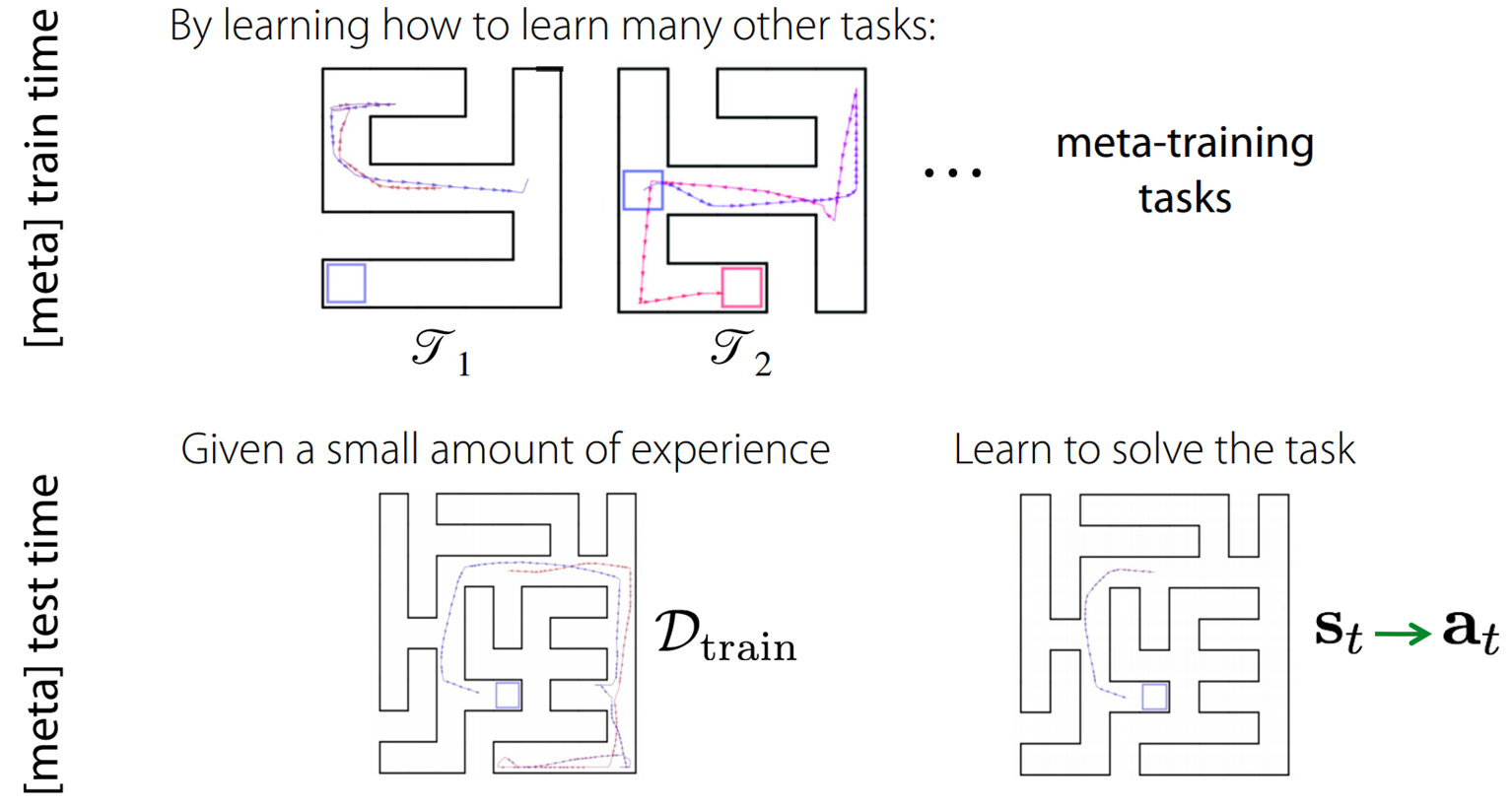
図3は迷路探索でのメタ強化学習の例を表しています。図3上段のように、$p(\mathcal{T})$からランダムにサンプリングした(ゴール位置や形状が異なる迷路で構成される)複数のタスク$\mathcal{T}_i\ (i=1,\ldots,N)$上での経験を用いてメタ訓練を行い、図3下段のように新しく与えられたタスク$\mathcal{T}$においてかなり早く最適な方策を見つけることができています。図3の例では、新たなタスクに対して2エピソードの試行で最適な方策を見つけることができています。
通常の強化学習とメタ強化学習における問題設定の比較すると以下のようになります。
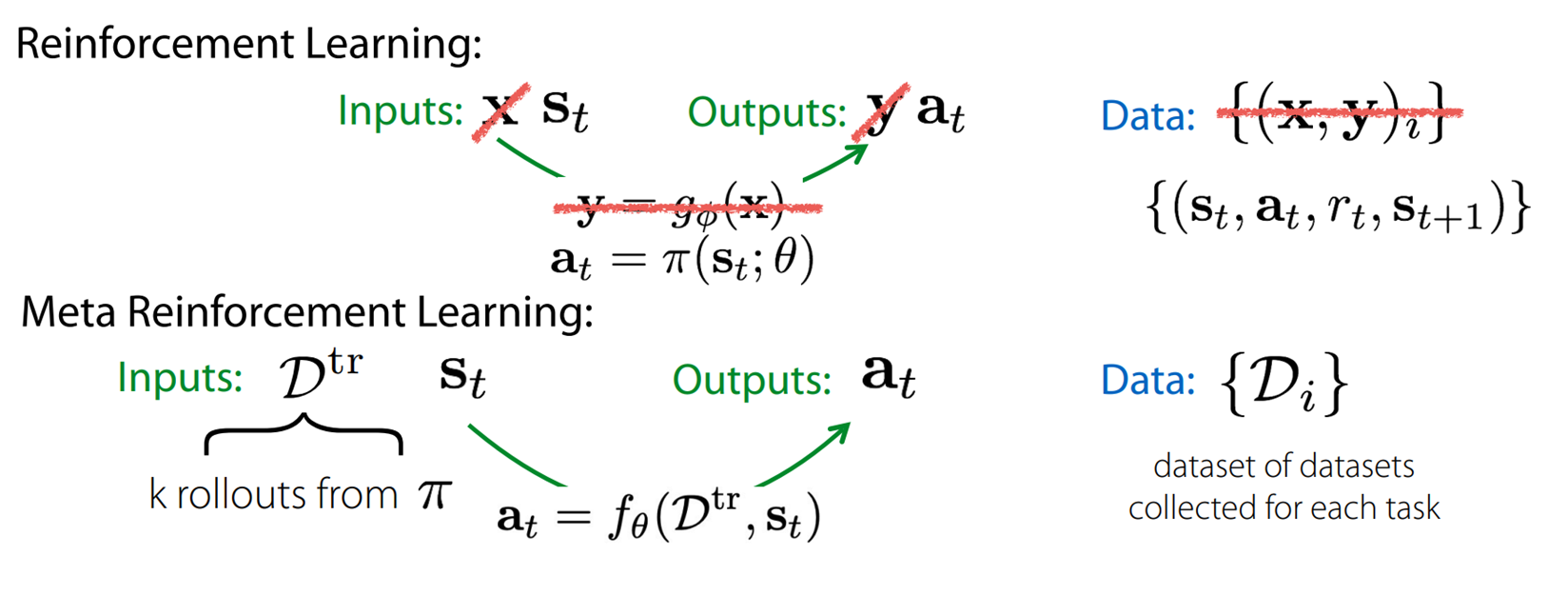
図5. 強化学習とメタ強化学習の比較(C. Finnのスライドより)
通常の強化学習では時刻$t$における状態$s_t$から時刻$t$における行動$a_t$を出力する方策関数$\pi_\theta(s_t)$をタスク上でサンプリングしたデータを基に学習します。一方で、メタ強化学習では対象のMDP上における数回(少量)のロールアウトによって得られたデータ$\mathcal{D}_{\mathrm{train}}$および状態$s_t$を入力とし、行動$a_t$を出力する関数$f$を他のタスク上でのサンプリングによって得られたデータ$\{\mathcal{D}_i \}$を基に学習することが目標となります。他のタスクでの経験を使う分、対象のタスク上でのロールアウトは数回で済みます。以下では代表的なメタ強化学習手法として、
・RNNベースの方法
・勾配ベースの方法
・変分推定法を用いる方法
を順に紹介していきます。
RNNベースのメタ強化学習
最初に、RNNベースのメタ強化学習法を紹介します。教師あり学習で紹介した方法と似た方法で、シンプルに実装できるといった利点があります。具体的には、タスクの分布$p(\mathcal{T})$からいくつかのタスク$\mathcal{T}_i$をサンプリングし、各タスク$\mathcal{T}_i$に対して図6のようなモデルを用いて、
① 現時刻の状態$s_t$、即時報酬$r_t$および前の時刻から引き継いだ隠れ状態を基に行動$a_t$を出力
② $a_t$を環境に適用して$s_{t+1}$と$r_{t+1}$を取得
を繰り返して累積報酬を計算します。そして、全$\mathcal{T}_i$に対する累積報酬の平均を目的関数とし、方策勾配法によってRNNのパラメータを更新していく形で学習が行われます。
ここでポイントとなるのが、RNNはエピソードをまたいでつなげるということです。これによって効率的な探索方法を学習することができます。
RNNモデルの学習後はRNNのパラメータを固定し、与えられたタスク$\mathcal{T}$上で手順1,2を学習済みのモデルに対して適用することでタスク$\mathcal{T}$に徐々に適用し、適切な行動$a_t$を出力できるようになります。
RNNベースの方法はこれまでに色々なモデルによって試されています。代表的なものとしては、
「RL2: Fast Reinforcement Learning via Slow Reinforcement Learning」
https://arxiv.org/pdf/1611.02779.pdf
「A Simple Neural Attentive Meta-Learner」
https://arxiv.org/pdf/1707.03141.pdf
などがあります。
勾配ベースのメタ強化学習(MAML)
次に、Model-Agnostic Meta-Learning(MAML)を見ていきます。MAMLは最もよく知られるメタRL手法の一つで、以下の論文で発表されました。
「Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks」
https://arxiv.org/pdf/1703.03400.pdf
MAMLは図7に示すように、「各タスクの最適な方策パラメータ$\theta_i^*$に数回の更新で到達できるようなパラメータ$\theta$を事前学習する」手法です。
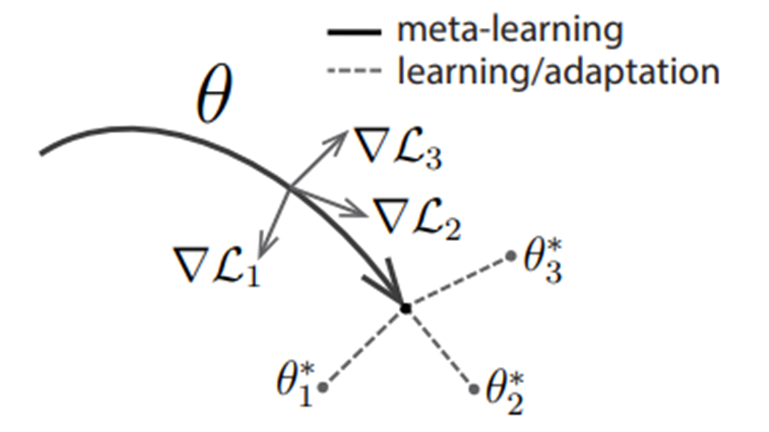
図7. MAMLの概念図
メタ訓練の詳しい手順は下記Algorithmに示しています。まずパラメータ$\theta$をランダムに初期化し、全ての訓練タスク$\mathcal{T}_i\ (i=1,\ldots,N)$に対して$\theta$でパラメトライズされた方策$\pi_\theta$を用いてサンプリングを行い$K$個の軌道を生成します。そして得られた軌道を用いて方策勾配法を適用し、各タスクに対する報酬関数の負値で定義されるコスト関数
$\mathcal{L}_{\mathcal{T}_i}(\pi_\theta)=-\mathbb{E}_{\pi_\theta}\left[
\sum_{t=1}^{H}R_i(x_t,a_t) \right]$
の推定勾配を取得し、勾配降下方向に更新したパラメータ$\theta_i'\ (i=1,\ldots,N)$を
$\theta_i'=\theta-\alpha\nabla_\theta \mathcal{L}_{\mathcal{T}_i}(\pi_\theta)$
によって計算します(Algorithm 7行目)。次に、パラメータ$\theta_i'$による方策を用いて各タスクに対してサンプリングを行い、タスク毎に軌道をいくつか生成します。そして、得られた軌道を用いて全タスクの累積報酬の期待値の総和の勾配を計算し、メタパラメータ$\theta$を更新します(Algorithm10行目)。
この操作を繰り返すことにより、「各タスクの方策勾配方向に更新すると各タスクに対する最適なパラメータに到達するような初期パラメータ$\theta$」が学習されることになります。
メタ訓練後は新しく与えられたタスク$\mathcal{T}$上での数回のパラメータ更新(Algorithm の7行目と同じ操作)によってそのタスクに適応した最適なパラメータ$\theta^*$が得られます。

変分推定法を用いたメタ強化学習(PEARL)
続いて、変分推定法を用いたメタ強化学習法として良く知られているPEARLを紹介します。PEARLは以下の論文で発表された手法になります。
「Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables」
https://arxiv.org/pdf/1903.08254.pdf
論文内で主張されている他の手法と比べたPEARLの利点は以下の2点です。
・off-policyのactor-critcでメタ訓練できるため、メタ訓練におけるサンプリング効率が向上
・posterior sampling によって各タスクを表す変数$z$をサンプリングできるので効率的な探索が可能(後述)
前述のRNNベースの方法や勾配ベースの方法などの従来法では、メタ訓練後に新しく与えられたタスクに対して制御を行う際に、on-policyで制御を実施する必要があるため、それに合わせてメタ訓練もon-policyで行う必要がありました(メタ訓練と学習後の制御実行が同じ操作でなければならないため)。例えば、RNNベースの手法では、タスク上での経験を入力として取り入れてタスクに適応するNNと現在の状態から方策を出力するNNは共通であり、実行時にはon-policyなデータを方策のNNモデルに入力していくことになります。そのため、メタ訓練時にもon-policyなデータを用いて学習する必要があります。
これに対してPEARLでは、与えられたタスク$\mathcal{T}$上での経験$c_{1:N}^{\mathcal{T}}$を入力とし、各タスクを表す確率変数$z$を出力とするNNモデル$q_\phi(z\mid c_{1:N}^{\mathcal{T}})$のパラメータ$\phi$と最適方策$\pi_\theta^*(a_t\mid s_t,z)$のパラメータ$\theta$を変分推定法を用いて同時学習します(ここで、$c_{1:N}^{\mathcal{T}}$はあるタスク$\mathcal{T}$上での時刻$n$における一回のトランジションによって得られたデータを$c_n^{\mathcal{T}}=(s_n,a_n,r_n,s_n')$と定義し、そのデータを時刻$1$から$N$にわたって集めたものです)。これにより、タスク$\mathcal{T}$上での経験を取り込むNNモデルと方策のNNモデルが分離され、方策の学習に関してはoff-policyな手法を適用することが可能となります。さらに、PEARLでは経験を入力としてタスク変数$z$の確率分布を出力する$q_{\phi}(z\mid c)$が学習されるため、posterior sampling によってタスク変数$z$をサンプリングでき、従来法と比べて効率的な探索を行うことが可能となります。
では、ここから具体的な学習方法を見ていきます。変分推定法によると、目的関数$R$が対数尤度関数であると仮定すると、$R$の変分下界(ELBO)は次式によって与えられます。
$\mathbb{E}_{\mathcal{T}}[\mathbb{E}_{z\sim q_\phi (z\mid c^\mathcal{T})}[R(\mathcal{T,z})+\beta D_{KL}(q_\phi(z\mid c^\mathcal{T})\mid \mid p(z))]]$
ここで、$p(z)$は$z$の事前分布(ガウス分布)、$D_{KL}$はKL情報量を表しています。
KL情報量の項は、直観的には事前分布$p(z)$と事後分布$_\phi(z\mid c^\mathcal{T})$が必要以上に離れてしまい、メタ訓練用のタスクを過学習してしまうことを防ぐ役割をしています。変分推定に関する詳しい内容は以下などを参照ください。
https://qiita.com/kenmatsu4/items/b029d697e9995d93aa24
以降では、上式を最大化するようなパラメータ$\theta$および$\phi$を求めることを考えていきます。
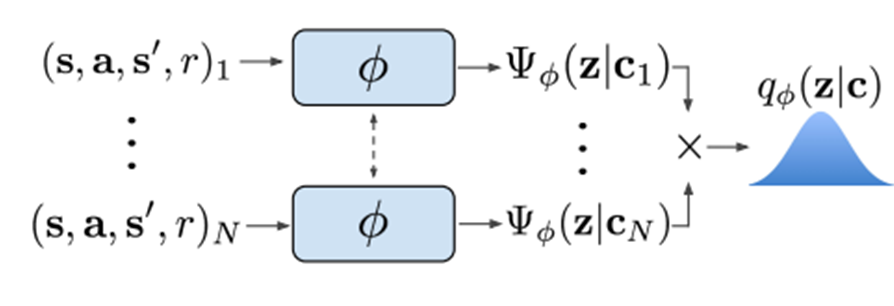
$z$の分布を予測する推定ネットワーク$q_\phi(z\mid c_{1:N}^{\mathcal{T}})$の具体的な構造としては以下のような構成が採用されています。
$q_\phi (z\mid c_{1:N})\propto \prod_{n=1}^N \Psi_\phi (z\mid c_n)$ ただし、$\Psi_\phi (z\mid c_n)=\mathcal{N}(f_\phi^{\mu}(c_n),f_{\phi}^{\sigma}(c_n))$
つまり、あるタスク$\mathcal{T}$上での各トランジションに対してモデル$\Psi_\phi$によって変数$z$の分布(ガウス分布)を出力し、これらすべての積をタスク$\mathcal{T}$を表す変数$z$の予測分布とします(permutation invarianceを仮定)。
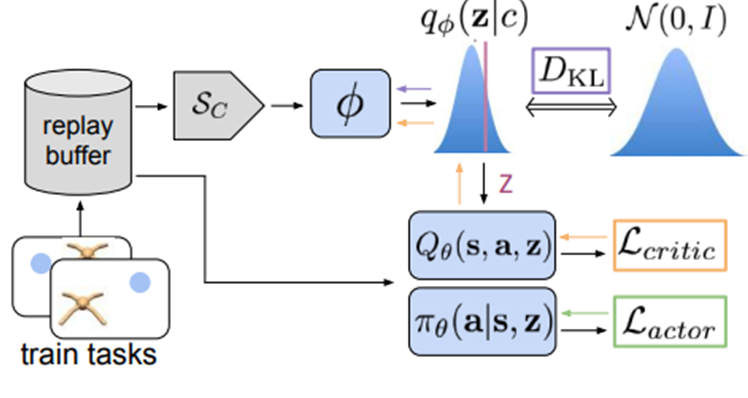
パラメータ$\phi$, $\theta$の学習(メタ訓練)は前述の通り、ELBOを最大化することを目的として図9および Algorithm 1 に示すように学習します。
パラメータ$\theta$の学習にはoff-policyのactor-critic法が採用されており、リプレイバッファに貯めたoff-policyなデータを用いて勾配を計算してパラメータを更新します。actor-criticアルゴリズムとしてはSoft Actor-Critc (SAC)が採用されています。SACについては説明を割愛しますが、以下の記事などで説明されています。
https://qiita.com/ku2482/items/fb79d8209f1162d9f141
$\phi$の更新および$z$を生成する際にはサンプラー$S_c$を通してバッファから抽出したデータを用います。サンプラー$S_c$は基本的に、より最近格納したデータから順に取り出すものになっています。メタテスト時に$q_\phi$にはon-plicyのデータが入ってくるので、$\phi$の更新にはなるべくon-policyのデータを使う必要があるため、$S_c$を通して抽出する形になっています。
メタ訓練後に新たに与えられたタスクに対する制御(メタテスト)は Algorithm 2 のようになっています。基本的には各パラメータは固定した状態で
- これまでの経験$c^\mathcal{T}$を用いて変数$z$をposterior sampling
- $\pi_\theta(a\mid s,z)$を用いてロールアウトし、得られたデータを$c^\mathcal{T}$に追加
を繰り返すことで、徐々に適切な$z$が得られるようになり、それに伴って得られる方策も最適なものに近づいていくことが期待できます。
モデルベースメタ強化学習
(追記予定)