今回紹介する論文はドメイン適応模倣学習に関する以下の二件です。
それぞれ2020年、2021年のICMLで発表された論文になります。
・Domain Adaptation Imitation Learning
https://arxiv.org/pdf/1910.00105.pdf
・Cross-domain Imitation from Observations
https://arxiv.org/pdf/2105.10037.pdf
前編の今回は前者の内容のみを説明し、後者の論文については後編にて説明予定です。
導入
模倣学習はエキスパート(熟練者)の行動から方策や報酬関数を学習する手法であり、ロボットの制御などでよく用いられる手法です。一般的な模倣学習に関する内容などは以下の記事などで触れられています。
https://qiita.com/3110atsu1217/items/c44130d59a0406b148c3
従来の模倣学習手法における制約の一つとして、エキスパートとエージェントのドメインが一致している必要があることが挙げられます。例えば、ロボットの制御を模倣学習によって行う場合には、エキスパートのロボットと制御したいロボットのダイナミクスや自由度が同じである必要があります(図1)。しかし実際的な運用を考えると、全く異なったダイナミクスや自由度を持つロボットが取った行動から方策を学習することができると非常に便利です(図2)。人間の場合だと、小さい子供が大人からスポーツの技術を学習したりすることができるので、感覚的には自然なアイデアであるようにも思われます。
今回紹介する文献では、上記のことをモチベーションとし、ドメインの全く異なるエキスパートのデモンストレーションを基に最適な行動を学習する模倣学習法を考えます。特に、先行研究とは異なり、ダイナミクス・視点・自由度などの違いをすべて考慮することができる包括的なフレームワークが提案されています。
 図 1. 従来の模倣学習(画像はboston dynamics社HPより)
図 1. 従来の模倣学習(画像はboston dynamics社HPより)
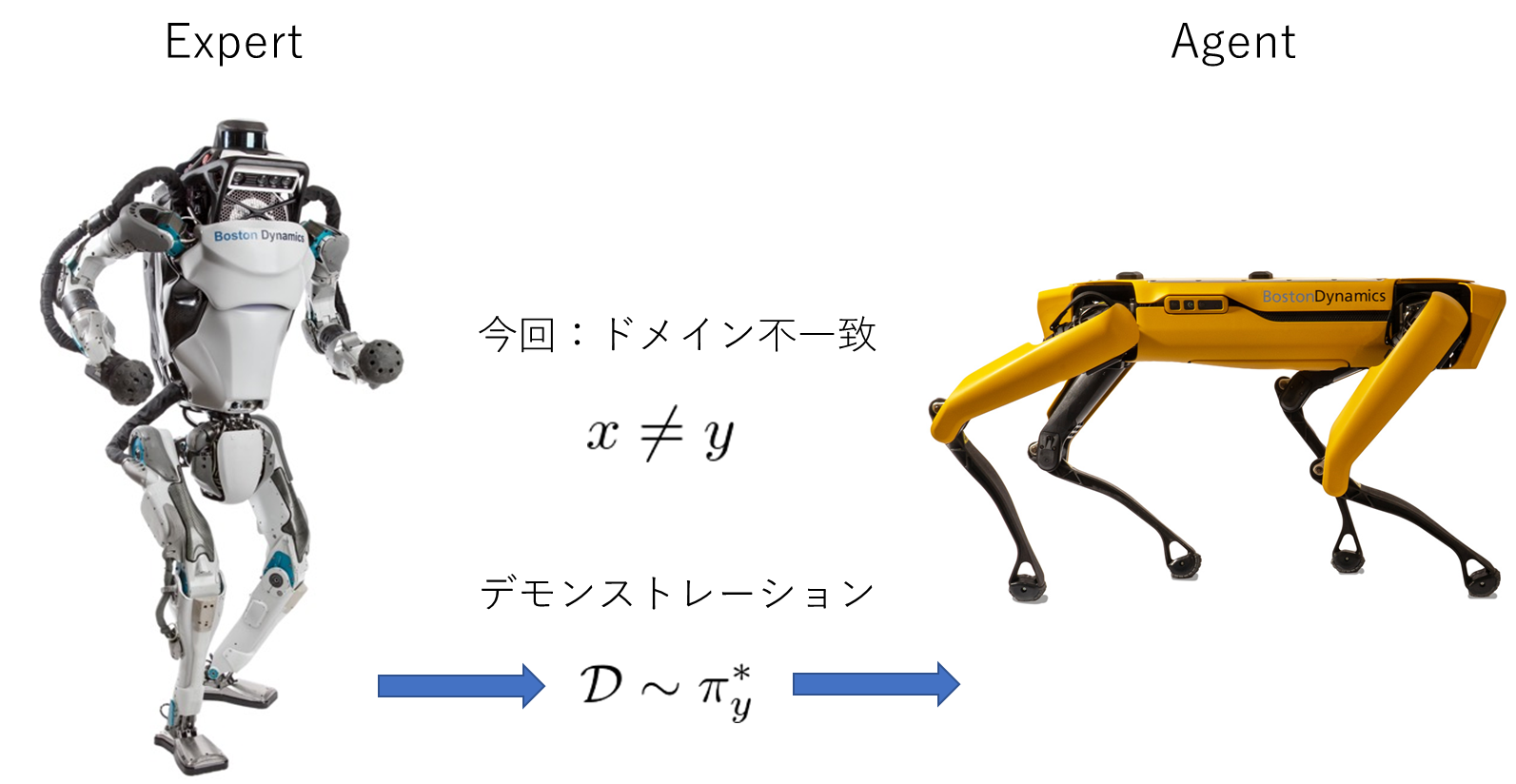 図 2. 今回考える模倣学習
## 関連研究
いくつか関連する研究をまとめておきます。ドメイン適応型の強化学習や模倣学習に関する内容はこれまでにも研究されていて、ダイナミクスが異なる場合の強化学習に関する先行研究としては
図 2. 今回考える模倣学習
## 関連研究
いくつか関連する研究をまとめておきます。ドメイン適応型の強化学習や模倣学習に関する内容はこれまでにも研究されていて、ダイナミクスが異なる場合の強化学習に関する先行研究としては
「Learning invariant feature spaces to transfer skills
with reinforcement learning」
https://openreview.net/pdf?id=Hyq4yhile
視点が異なる場合の模倣学習に関しては
「Imitation from Observation: Learning to Imitate Behaviors from Raw Video
via Context Translation」
https://digitalassets.lib.berkeley.edu/techreports/ucb/text/EECS-2018-37.pdf
「State alignment-based imitation learning」
https://arxiv.org/pdf/1911.10947.pdf
等があります。今回紹介する論文はダイナミクスや自由度、視点などのドメイン間の違いをすべて同時に考慮することができ、かつ後程説明するように時間的なずれがあるデータを用いて学習できるといったことが他の研究と比べた主な新規性になっているようです。
定義(MDPなど)
ここでは必要な定義をいくつかまとめます。
◆ マルコフ決定過程 (MDP)
MDPは5つの要素からなるタプル$\mathcal{M}=(\mathcal{S},\mathcal{A},\mathcal{P},\eta,\mathcal{R})$で定義されます。$\mathcal{S}$, $\mathcal{A}$はそれぞれ状態空間、行動空間を表し、$P:\mathcal{S}\times \mathcal{A}\rightarrow \mathcal{S}$はトランジション、$\mathcal{R}$は報酬、$\eta$は初期状態の分布を表します。MDPは強化学習で非常に重要な概念ですが、ここでは詳しい説明は割愛します。このあたりの説明については強化学習の基本を詳しく説明している以下の記事などを参照ください
https://qiita.com/icoxfog417/items/242439ecd1a477ece312
◆ドメイン
冒頭から何度か登場している「ドメイン」についてですが、ここでは報酬を除いたMDP $(\mathcal{S}, \mathcal{A}, \mathcal{P}, \eta)$ によって定義されます。つまり、ドメインにはロボットのダイナミクスなどの情報を含んだトランジション$\mathcal{P}$や自由度に関する情報などを含んだ状態・行動空間$\mathcal{S}$, $\mathcal{A}$が含まれていますが、望ましい振る舞いに関する情報を含む報酬$\mathcal{R}$は含まれません。
◆ 各タスク・ドメインに対応するMDP
タスク$\mathcal{T}$に対するドメイン$x$のMDPを$\mathcal{M}_{x,\mathcal{T}}=(\mathcal{S}_x, \mathcal{A}_x, \mathcal{P}_x, \eta_x, R_{x,\mathcal{T}})$と表すこととします。タスク$\mathcal{T}$は最適な振る舞いを規定するものであり、「歩く」などといった所望の振る舞いをラベル付けするものになっています。$R_{x,\mathcal{T}}$はタスク$\mathcal{T}$によって決まる報酬を表しています。
◆ デモンストレーション
デモンストレーションはエキスパートが取った状態・行動対の軌道であり、ドメイン$x$におけるタスク$\mathcal{T}$に対するデモンストレーションを$\tau_{\mathcal{M}_{x,\mathcal{T}}}=\{ (s_x^{t},s_x^{t}) \}_{t=1}^{H}$で定義します。また、デモンストレーションを複数集めた集合を$\mathcal{D}_{\mathcal{M}_{x,\mathcal{T}}}$と表すこととします。模倣学習では、このデモンストレーションを基にエージェントが自身の好ましい行動を学習することになります。
提案手法の概要
まず、$\mathcal{M}_{x,\mathcal{T}}$と$\mathcal{M}_{y,\mathcal{T}}$をそれぞれタスク$\mathcal{T}$に対するセルフドメイン$x$およびエキスパートドメイン$y$のMDPとします。このとき、ドメイン適用模倣学習における最終的な目標は「ドメイン$x$での最適報酬$\pi^*_{x,\mathcal{T}}$をエキスパートのデモンストレーション$\mathcal{D}_{\mathcal{M}_{y,\mathcal{T}}}$を基に、報酬$R_{x,\mathcal{T}}$に関する情報を用いることなく学習すること」です。
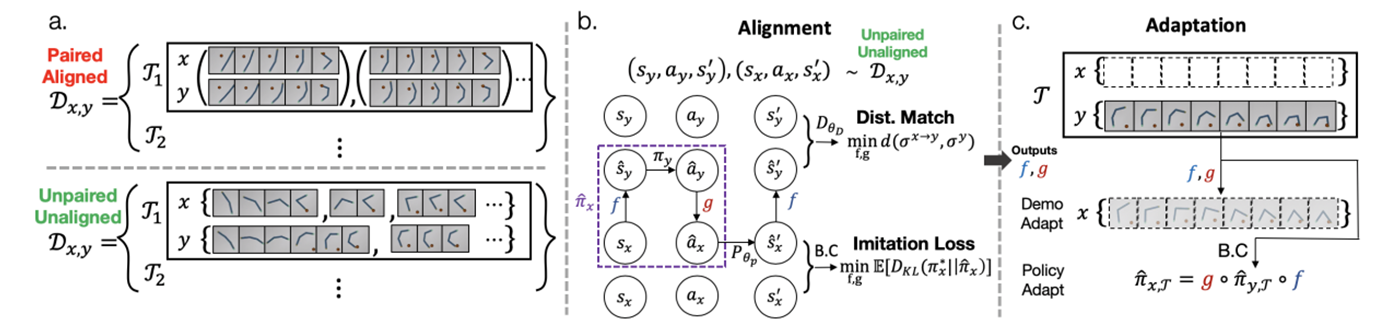
ここでは、上記の目標を達成するための提案手法の流れを簡単に説明します。提案手法の全体的な概要図は図 3 のようになっています。提案手法は以下の二つのステップからなっており、これらを順に説明していきます。
-
MDP alignment
-
ゼロショット適応
1. MDP aligment
MDP aligmentにおける目標は、状態$s_x\in \mathcal{S}_x$をドメイン$y$に移す関数$f\ :\ \mathcal{S}_x \rightarrow \mathcal{S}_y$および、ドメイン$y$での行動$a_y\in \mathcal{A}_y$をドメイン$x$に移す関数$g\ : \mathcal{A}_y \rightarrow \mathcal{A}_x$を適切に学習することです(図3中央)。これにより、
①ドメイン$x$の状態$s_x$を関数$f$によってドメイン$y$の状態$s_y$に移す
② デモンストレーション$\mathcal{D}_{\mathcal{M}_{y,\mathcal{T}}}$によって学習した方策$\pi_{y,\mathcal{T}}$によってドメイン$y$上で
の最適な行動$a_y$を生成する
③ 得られた行動を関数$g$によってドメイン$x$上での行動$a_x$に移す
という手順によって、ドメイン$x$上での最適な行動をドメイン$y$上のデモンストレーションのみを用いて得ることができるようになります。
MDP alignmentの学習では、タスクに依存しない"一般的な"ドメイン間のalignmentを得るために、複数のタスク$\mathcal{T}_i,\ (i=1,2,\ldots,N)$に対する両ドメイン上でのデモンストレーション$\mathcal{D}_{x,y}=\{(\mathcal{D}_{\mathcal{M}_{x,\mathcal{T}_i}},\mathcal{D}_{\mathcal{M}_{y,\mathcal{T}_i}})\}_{i=1}^N$を学習データとして用います(図 3 左)。ここで、両ドメインのデモンストレーションは、図 3 左下のように同じステップにおける状態・行動が1対1に対応していなくても構いません。図 3 左下の例では、タスク$\mathcal{T}_1$に対するドメイン$x$での最初の4ステップ分のデモンストレーションがドメイン$y$の最初の6ステップ分のデモンストレーションに対応しており、時間的にずれています。このようなunalignedなデータで学習できることも本手法の特色の一つです。[](また、$\mathcal{D}_{\mathcal{M}_{x,\mathcal{T}}}$を使うことに違和感があるかもしれませんが、MDP aligmentの時の段階では両ドメインのデモンストレーションが必要であることにご注意ください。一度MDP alignmentの学習が終わると、後述のように新しく与えられた に対して...。)
具体的な関数$f$, $g$の学習方法については、後述します。
2. ゼロショット適応
MDP aligment で適切な関数$f$および$g$が学習できれば、あとは通常の模倣学習の適用によって目標を達成することができます。具体的には、新しく与えられたタスク$\mathcal{T}$に対するドメイン$y$上でのデモンストレーション$\mathcal{D}_{\mathcal{M}_{y,\mathcal{T}}}$を用いて行動クローニングなどの一般的な模倣学習手法によってドメイン$y$上での方策$\pi_{y,\mathcal{T}}$を学習し、上で述べた①~③の手順に従ってドメイン$x$上での方策を得ることができます(図 3 右)。
ゼロショット適応については従来の模倣学習の適用で実行できるため、以降ではMDP alignment に関する内容を中心に説明していきます。
MDP alignment の定式化
まず、前述のMDP alignment を定式化していきます。その上で、以下のMDP reduction が重要となります。
■ 定義 1 (MDP reduction)
以下の条件 1, 2を満たす二つの関数$\phi : S_x \rightarrow S_y$および$\psi : A_x \rightarrow A_y$からなるタプル$(\phi,\psi)$を$\mathcal{M}_{x,\mathcal{T}}$から$\mathcal{M}_{x,\mathcal{T}}$へのMDP reductionと呼ぶ。
1.($\pi$-最適性)
任意の$(s_x,a_x,s_y,a_y)\in \mathcal{S}_x\times \mathcal{A}_x\times \mathcal{S}_y \times \mathcal{A}_y$に対して、
$O_{\mathcal{M}_y}(\phi(s_x),\psi(a_x))=1 \rightarrow O_{\mathcal{M}_x}(s_x,a_x)=1,$
$O_{\mathcal{M}_y}(s_y,a_y)=1 \rightarrow \phi^{-1}(s_y)\neq\emptyset, \psi^{-1}(a_y)\neq\emptyset$
- (ダイナミクス)
$O_{\mathcal{M}_y}(s_y,a_y)=1$, $s_x \in \phi^{-1}(s_y)\neq \emptyset$および$\psi^{-1}(a_y)\neq\emptyset$を満たす任意の
$(s_x,a_x,s_y,a_y)\in \mathcal{S}_x\times \mathcal{A}_x\times \mathcal{S}_y \times \mathcal{A}_y$に対して、
$P_y(s_y,a_y)=\phi(P_x(s_x,a_x))$
ただし、$O_{\mathcal{M}}(s,a)$は状態$s$に対して行動$a$が最適である場合に値1を取り、そうでないときに値0を取る関数
1はドメイン$y$における最適な状態・行動のペアに対応するドメイン$x$における最適な状態・行動のペアが存在し、その写像が全射である関数$\phi$, $\psi$によって表されることを要求しています。
また、2はドメイン$y$での状態遷移に対応する状態遷移がドメイン$x$にも存在し、その対応関係が関数$\phi$によって表されることを要求しています。
論文内では、ドメイン$x$から$y$またはドメイン$y$から$x$へのMDP reduction が存在するとき、$\mathcal{M}_x$と$\mathcal{M}_y$はalinableであると定義されています。特に、ドメイン$x$から$y$へのreduction $(\phi,\psi)$が存在する場合には、ドメイン$y$での最適な状態・行動を関数$(\phi,\psi)$によってドメイン$y$に移すことができるので、前述の関数$f$, $g$はMDP reductionとなるように($f=\phi$, $g^{-1}=\psi$となるように)学習すればよいことになります。学習においては以下の問題のように、より一般的なMDP alignment を得るために、複数のタスクに対するMDP reductionの共通部分を求めることを考えます。イメージとしては下図のような形で、複数タスクのMDP reductionの共通部分を取ることで、学習によって得られるreductionがターゲットタスク$\mathcal{T}$のreductionになる可能性が上がります。
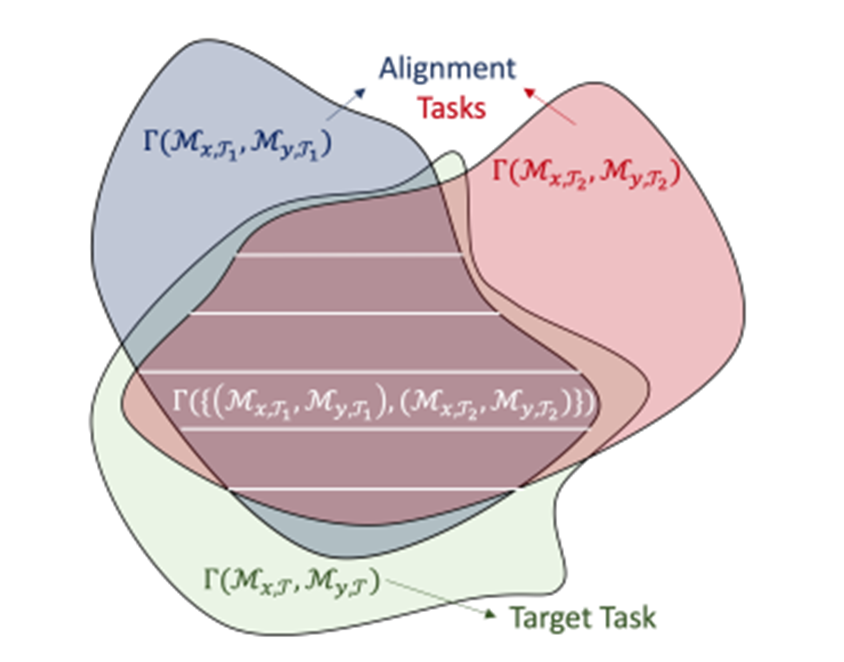
■ 問題 (MDP alignment)
ターゲットタスク$\mathcal{T}$に対するMPDのペアを$(\mathcal{M}_{x,\mathcal{T}},\mathcal{M}_{y,\mathcal{T}})$とする。
このとき、$N$個のMDPペア$\{ (\mathcal{M}_{x,\mathcal{T}_i},\mathcal{M}_{y,\mathcal{T}_i}) \}_{i=1}^{N}$に対するデータセット
$\mathcal{D}_{x,y}=\{ \mathcal{D}_{\mathcal{M}_{x,\mathcal{T}_i}}, \mathcal{D}_{\mathcal{M}_{x,\mathcal{T}_i}} \}_{i=1}^{N}$をもとにMDP reduction $(\phi,\psi)\in\Gamma(\{\mathcal{M}_{x,\mathcal{T}},\mathcal{M}_{y,\mathcal{T}}\}_{i=1}^{N})\subset \Gamma(\mathcal{M}_{x,\mathcal{T}},\mathcal{M}_{y,\mathcal{T}})$を求めよ
ただし、$\Gamma(\mathcal{M}_x,\mathcal{M}_y)$は全ての$\mathcal{M}_x$から$\mathcal{M}_y$へのMDP reduction の集合を表し、$\Gamma(\{\mathcal{M}_{x,\mathcal{T}_i},\mathcal{M}_{y,\mathcal{T}_i}\}_{i=1}^{N})$は全$\Gamma(\mathcal{M}_{x,\mathcal{T}_i},\mathcal{M}_{y,\mathcal{T}_i})$の積集合を表します。
MDP alignment の学習
ここからは具体的な学習方法を見ていきます。まず、ドメイン$y$を経由した方策$\hat{\pi}_{x}$を以下のように定義します。
■ 定義 2 (co-domain policy execusion process)
$s_x^{(0)}\sim \eta_x$, $\ \hat{s}^{(t)}_y=f(s_x^{t})$, $\ \hat{a}_y^{(t)}\sim \pi_{y}(\cdot \mid \hat{s}^{(t)}_y)$, $\ a_x^{(t)}=g(\hat{a}_y^{(t)})$,
$s_x^{(t+1)}=P_x(s_x^{(t)}, a_x^{(t)})$
つまり方策$\hat{\pi}_{x}$は、ドメイン$x$の状態を関数$f$でドメイン$y$に移す → ドメイン$y$の方策を用いて行動を決定 → その行動を関数$g$によってドメイン$x$に移す。というプロセスで得られた方策になります。このとき、次のような二つの分布$\sigma_{\pi_y}^y$と$\sigma^{x\rightarrow y}_{\hat{\pi}_x}$を考えます。
$\sigma_{\pi_y}^y(s_y,a_y,s_y')=$
$\lim_{T\rightarrow \infty} \frac{1}{T}\sum_{t=0}^{T} \mathrm{Pr}\left(s_y^{(t)}=s_y, a_y^{(t)}=a_y,s_y^{(t+1)}=s_y'\mid \pi_y\right)$
$\sigma^{x\rightarrow y}_{\hat{\pi}_x}(s_y,a_y,s_y')=$
$\lim_{T\rightarrow \infty} \frac{1}{T}\sum_{t=0}^{T} \mathrm{Pr}\left(\hat{s}_y^{(t)}=s_y, \hat{a}_y^{(t)}=a_y,\hat{s}_y^{(t+1)}=s_y'\mid \mathcal{P}_{\hat{\pi}_x}\right)$
前者は単純なドメイン$y$上での状態遷移の確率分布になっていて、後者はドメイン$x$でのトランジション$\mathcal{P}_{\hat{\pi}_{x}}$を経由した場合のドメイン$y$上の状態遷移の分布となっています。学習における最終的な目標は以下の2点を最適化することです。
◆ 方策$\hat{\pi}_{x}$の最適性
◆ $\sigma_{\pi_y}^y$と$\sigma^{x\rightarrow y}_{\hat{\pi}_x}$の一致性
前者はMDP alignment の定義(定義 1)の性質 1 に対応し、後者は性質 2に対応しています。上記の目標のための最適化問題は抽象的に以下のように書くことができます(図 3 中央参照)。
$\min_{f,g} - J(\hat{\pi}_x)+\lambda d(\sigma^{x\rightarrow y}_{\hat{\pi}_x},\sigma_{\pi_y}^y)$
ここで、$J$は方策の性能を表す関数で、$d$は確率分布間の"距離"を表す関数、$\lambda$は双対変数です。本研究では特に、この最適化問題を敵対的生成ネットワーク(GAN)に基づいて解くことを考えます。GANについては以下などを参照ください。
https://ledge.ai/gan/
具体的には、上の最適化問題を以下のように書き直します。
$\min_{f,g} \max_{D_{\theta_{D}^{i}}} \sum_{i=1}^{N}\left( \mathbb{E}_{s_x\sim \pi^{*}_{x,\mathcal{T}_i}}[D_{KL} (\pi^{*}_{x,\mathcal{T}_i}||\hat{\pi}_{x,\mathcal{T}_i}(\cdot|s_x))] + \lambda (\mathbb{E}_{\pi^{*}_{y,\mathcal{T}_i}}\ [ \log D_{\theta_{D}}(s_y, a_y,s_y') ]+\mathbb{E}_{\pi^{*}_{x,\mathcal{T}_i}}\ [ 1-\log D_{\theta_{D}}(\hat{s}_y, \hat{a}_y,\hat{s}_y') ])\right)$
ここで、$D_{KL}$はKLダイバージェンスで、直観的には二つの分布の離れ具合を表しています。また、$D_{\theta_D}$はGANのDiscriminatorを表しています。
基本的にはGANのDiscriminator $D_{\theta_D}$のパラメータ$\theta_D$は実際のトランジションと"偽の"トランジションを区別するように学習し、関数$f$と$g$のパラメータは$\hat{\pi}_x$が最適となり(ドメイン$x$での真の最適方策$\pi^{*}_{x,\mathcal{T}_i}$と$\hat{\pi}_{x,\mathcal{T}_i}$の分布が近くなるように)、かつDiscriminatorを騙すように学習することになります。実際には、$D_{KL} (\pi^{*}_{x,\mathcal{T}_i})||\hat{\pi}_{x,\mathcal{T}_i})$の部分はドメイン$x$上でのデモンストレーション内の行動$a_x$との比較によって評価されます。
最後に、以下にMDP alignment のアルゴリズムを示します。

ダイナミクスを表す${P}_{\theta_P^x}$, discriminator $D_{\theta_D}$, 関数 $f_{\theta_f}$ および $g_{\theta_g}$の4つのニューラルネットワークのパラメータを順に勾配方向に更新し、上の最適化問題の鞍点に収束させるようなアルゴリズムとなっています。