敵対的模倣学習(Generative Adversarial Imitation Learning)という学習手法を紹介します。
模倣学習(Imitation Learning)とは?
強化学習分野に類似の枠組みで、「何が良い行動か」を定義する数値を人間が天下りに与えるのではなく、行動履歴の事例から習得させる枠組みです。
強化学習の枠組みと報酬設計の問題点
エージェント&環境
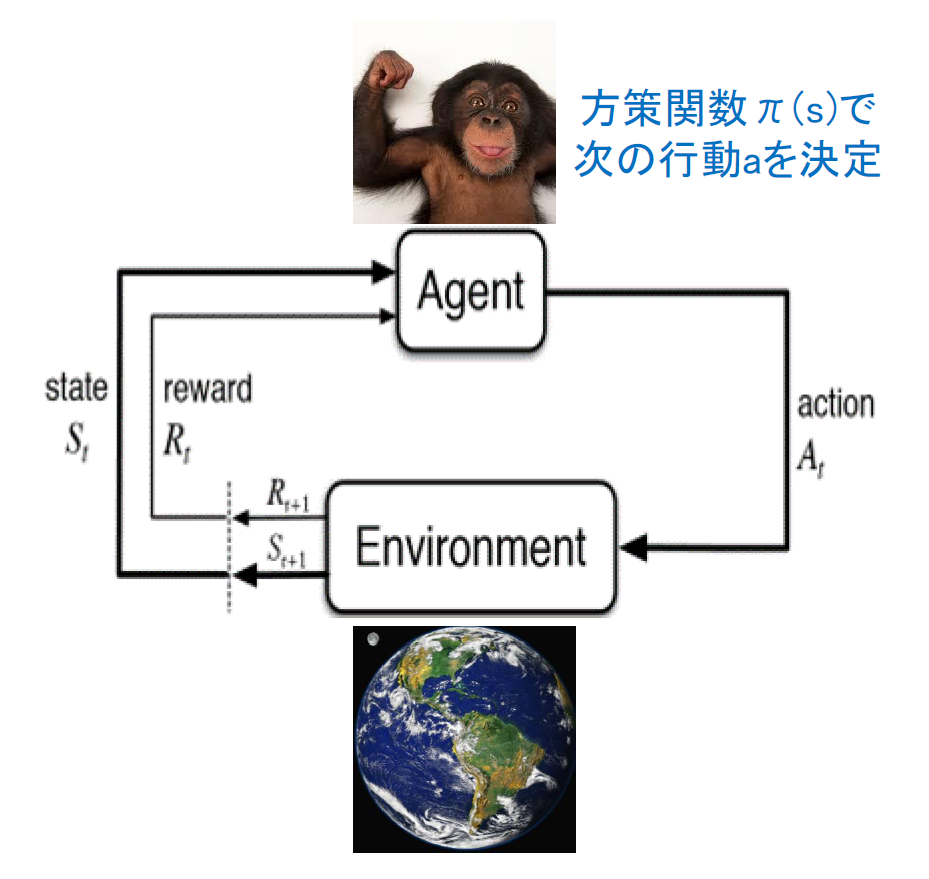
よくある強化学習のエージェントと環境の模式図は以下のように書かれます。
とはいえ、環境から与えられる報酬の設計が設計者の直感通りに上手く行くとは当然限りません。
報酬関数は人間の意図通り動作するとは限らない
古典的な例がOpenAIのブログ ( https://blog.openai.com/faulty-reward-functions/ ) で紹介されています。
このゲームでは、サークルコースをボートで巡回しながら、シューティングもするゲームですが、コース周回だけでなくシューティングすることに対しても報酬を与えた時に、コースも同時に回ってくれるだろうと期待していました。ところが、一箇所で旋回しながらシューティングだけを繰り返して、サークルコースを全く巡回しない「学習」をしてしまったという事例です。
そこで、「常識ある人間ならコースがあれば回ってくれるような行動もするし、シューティングもするよね」という事例から、どのような行動を選択するべきかの尺度を習得しようという発想がでてきます。常識ある人間の行動の軌跡をエキスパート軌跡(Expert Trajactory)と呼びます。常識ある人間が状態に対してどのように行動を選択するかの分布をエキスパート方策(Expert Policy)と呼びます。
模倣学習の従来の手法と敵対的模倣学習の違い
行動模倣( Behavioral Cloning )
一番素朴な発想です。
この状態が来たらエキスパート軌跡での行動は何か?を教師ありで予測させます。
しかし、データが大量に必要だったりする & 状態の分布(入力分布)が変化したけど、状態に対して取るべき行動の分布(入力値で条件付けられた出力分布)が不変の場合などに問題があります。
逆強化学習 (Inverse Reinforcement Learning) による報酬関数の推定
もうちょっと、迂回したやりかたとして、以下の2段階を踏むことも提案されて、そのうちの一部分が逆強化学習という分野をなしています。
1(IRL-step):状態&行動ペアに対してどれくらい取るべき軌跡に近いかのスコア(=報酬関数)のモデルを学習
2(RL-step):学習済みモデルを報酬関数に置き換えて、通常の強化学習のアルゴリズムを実行
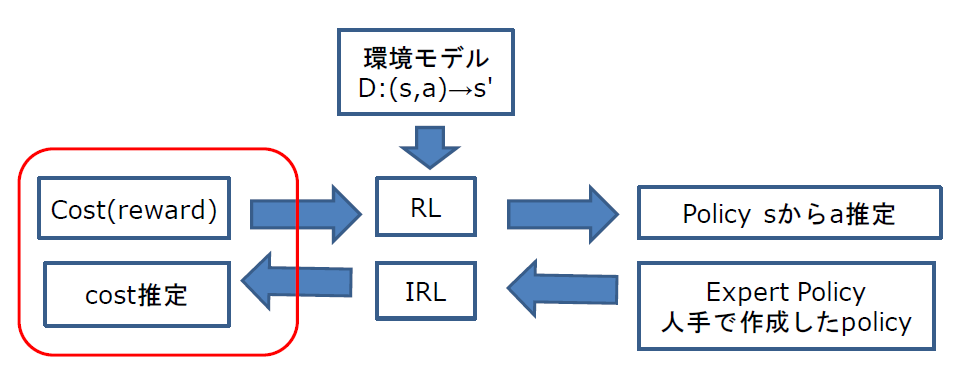
これを、図で表現すると以下のようになります。
左側から右側への矢印が1:のIRL stepに対応しています。右側から左側への矢印が2:のRL stepに対応しています。
しかしながら、2段階の学習のコストがかかってしまうという問題がありました。
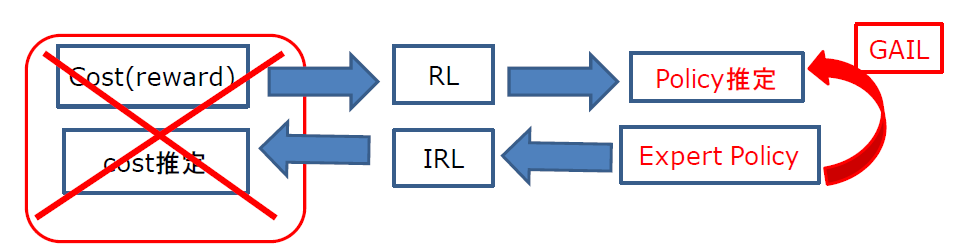
そこで、以下のようにIRLとRLのパイプラインを省略して Expert から直接Policyを推定したいという発想がでてきます。
これを実現したのが敵対的模倣学習(Generative Adversarial Imitation Learning = GAIL)です。
実は、「敵対的」というのは報酬関数(上図の cost )を限定した形状(ある凸関数)に固定すると、更新式にGAN(Generative Adversarial Netwrok)と同様の更新式が出現するということから名前が付けられているだけです。(この説明は不正確かもしれませんが、、、)
なので、別の形状の関数に固定すると別の手法になる可能性もあります。
詳細は、数式や証明が煩雑になるのでここでは省略します。原論文 ( https://arxiv.org/pdf/1606.03476.pdf ) に詳細があります。
手法の概略
Episode ごとに以下を繰り返します。
1:方策のネットワークを固定して行動させることで軌跡を採取
2:Discriminatorのネットワークの重みをExpertの軌跡と方策の生成した軌跡を入力してGANの損失関数によって学習
3:方策を更新するためのターゲットに必要なAdvantageの値と収益の値を価値関数のネットワークから計算
4:PPOの更新式によって、方策のネットワークと価値観数のネットワークを計算
以下では、ステップ2:, 3:, 4:について、pytorchのソースを使って説明します。(原論文では4:でTRPOを用いていますが、TRPOは複雑なのでTRPOの近似手法であるPPOを用います。)
Discriminatorと方策と価値関数に対応して3種類のネットワークを定義する必要がありますが、ネットワークの構造はいずれも単純なMLPです。
方策のネットワークを固定して行動させることで軌跡を採取
方策のネットワークは以下のように定義されます。以下の例では、方策の出力は、離散値の行動の確率分布です。確率分布のテンソルからmultinomialで入力された状態表現ベクトルからsample_actionによってひとつの整数を取得します。
class PolicyNet(nn.Module):
def __init__(self, dim_state, num_action, hidden_sizes=(100, 100), activation=torch.tanh):
super().__init__()
self.affine_layers = nn.ModuleList()
last_in_dim = dim_state
for out_dim in hidden_sizes:
self.affine_layers.append(nn.Linear(last_in_dim, out_dim))
last_in_dim = out_dim
self.action_head = nn.Linear(last_in_dim, num_action)
self.action_head.weight.data.mul_(0.1)
self.action_head.bias.data.mul_(0.0)
def forward(self, x):
for affine in self.affine_layers:
x = self.activation(affine(x))
action_prob = torch.softmax(self.action_head(x), dim=1)
return action_prob
def sample_action(self, state):
action_prob = self.forward(state)
action = torch.multinomial(action_prob, 1)
return action
def get_log_prob(self, x, actions):
action_prob = self.forward(x)
return torch.log(action_prob.gather(1, actions.long().unsqueeze(1)))
Expertか否かの分類
Networkの定義
class Discriminator(nn.Module):
def __init__(self, num_inputs, hidden_sizes=(100, 100), activation=torch.tanh):
super().__init__()
self._activation = activation
self._layers = nn.ModuleList()
last_in_dim = num_inputs
for out_dim in hidden_sizes:
self._layers.append(nn.Linear(last_in_dim, out_dim))
last_in_dim = out_dim
self.logits = nn.Linear(last_in_dim, 1)
self.logits.weight.data.mul_(0.1)
self.logits.bias.data.mul_(0.0)
def forward(self, x):
for linear in self._layers:
x = self._activation(linear(x))
prob = torch.sigmoid(self.logits(x))
return prob
損失関数は、2値クロスエントロピーを使用します。
disc_binary_cross_entropy = nn.BCELoss()
行動と状態をbatchの次元以外をtorch.catでconcatしてからDiscriminatorのネットワークに入力して損失関数を計算します。
expert_state_actions = torch.from_numpy(expert_traj).to(dtype).to(device)
g_o = discriminator_net(torch.cat([states, actions], 1))
e_o = discriminator_net(expert_state_actions)
optimizer_discrim.zero_grad()
discrim_loss = disc_binary_cross_entropy(g_o, ones((states.shape[0], 1), device=device))
discrim_loss += disc_binary_cross_entropy(e_o, zeros((expert_traj.shape[0], 1), device=device))
discrim_loss.backward()
optimizer_discrim.step()
方策関数と価値関数の更新
方策用のネットワークは既に定義しましたので、後は価値関数のネットワークを定義します。これも単純なMLPとなります。
class ValueNet(nn.Module):
def __init__(self, dim_state, hidden_sizes=(100, 100), activation=torch.tanh):
super().__init__()
self.activation = activation
self.layers = nn.ModuleList()
last_in_dim = dim_state
for out_dim in hidden_sizes:
self.layers.append(nn.Linear(last_in_dim, out_dim))
last_in_dim = out_dim
self.value_out = nn.Linear(last_in_dim, 1)
self.value_out.weight.data.mul_(0.1)
self.value_out.bias.data.mul_(0.0)
def forward(self, x):
for linear in self.layers:
x = self.activation(linear(x))
value = self.value_out(x)
return value
方策のネットワーク(Actor)と価値関数のネットワーク(Critic)を交互に更新するActor-Criticの一種であるPPO (Proximal Policy Optimization)の更新を実行します。
PPO更新の更新では
1:方策ネットワークとそのOptimizer
2:状態&行動
3:報酬と価値関数ネットワークの出力値に割り引き計算をして得られる収益とアドバンテージ
4:2:の状態&行動を入力とした方策のネットワークの行動の分布(対数スケール)の出力
5:PPOの方策出力を制限するためのクリップ値
6:SGDによる勾配のクリップ値
を使用して以下のように計算します。(3:&4:については、後ほど説明をします。)
def ppo_update(policy_net_and_optimizer,
value_net_and_optimizer,
states,
actions,
returns,
advantages,
target_log_probs,
clip_epsilon,
clip_grad_norm):
# Update Critic
value_net, optimizer = value_net_and_optimizer
values_pred = value_net(states)
value_loss = torch.mean(torch.pow((values_pred - returns), 2))
value_optimizer.zero_grad()
value_loss.backward()
value_optimizer.step()
# Update Actor policy
policy_net, policy_optimizer = policy_net_and_optimizer
log_probs = policy_net.get_log_prob(states, actions)
ratio = torch.exp(log_probs - target_log_probs)
bounds = [ratio * advantages, torch.clamp(ratio, 1.0 - clip_epsilon, 1.0 + clip_epsilon) * advantages]
bounded_policy = -torch.min(*bounds).mean()
policy_optimizer.zero_grad()
bounded_policy.backward()
torch.nn.utils.clip_grad_norm_(policy_net.parameters(), clip_grad_norm)
policy_optimizer.step()
torch.crampによって、強制的にratioの値域が制限されていることがPPO更新の特徴となります。
(原論文の更新に使用されているTRPO(Trust Region Policy Optimization)は、このようなクリップによって実現されている方策の限界をFisher情報行列によって定義された制約付き最適化問題を共役勾配法で計算するなど、込み入った手法です。)
さて、最後に
3:報酬と価値関数ネットワークの出力値に割り引き計算をして得られる収益とアドバンテージ
4:2:の状態&行動を入力とした方策のネットワークの行動の分布(対数スケール)の出力
についてです。
価値関数ネットワークの出力値と方策のネットワークの行動の分布(対数スケール)の出力については、計算グラフに対して.backward()で勾配が計算されないように注意します。
with torch.no_grad():
values = value_net(states)
target_log_probs = policy_net.get_log_prob(states, actions)
つまり、no_grad()によりvalues = & target_log_probs = では、逆伝搬は行われません。
収益とアドバンテージについては、時間に対する割引率gammaを用いて以下のように計算します。
def get_advantages_and_returns(rewards, dones, values, gamma, tau):
next_deltas = torch.zeros((rewards.size(0), 1))
next_advantages = torch.zeros((rewards.size(0), 1))
value = 0
advantage = 0
for t in reversed(range(rewards.size(0))):
next_deltas[t] = rewards[t] + gamma * value * dones[t] - values[t]
next_advantages[t] = next_deltas[t] + gamma * tau * advantage * dones[t]
value = values[t, 0]
advantage = next_advantages[t, 0]
return (next_advantages - next_advantages.mean()) / next_advantages.std(), values + next_advantages