3軸ロボットアーム Part1 (順運動学)

はじめに

私がロボットに関して興味を持っている．特にロボットの経路生成に興味がある．
前記事では，干渉物が存在する環境下で，2軸ロボットアームの経路生成を実装した．
(https://qiita.com/haruhiro1020/items/b42725df00e13ddcb5af)
本記事では，3軸ロボットアームの順運動学を説明する．
順運動学とは，関節角度から手先位置を計算することです．
手先位置を算出するために，三角関数(sin, cos, tan)を使用する．以下サイトはわかりやすいです．
・https://www.meikogijuku.jp/meiko-plus/study/trigonometric-function.html

本記事で実装すること

・3軸ロボットアームの順運動学

本記事では実装できないこと (将来実装したい内容)

・3軸ロボットアームの逆運動学 (逆運動学 ... ロボットの手先位置からロボットの関節角度を算出する)
・3軸ロボットアームに経路生成RRT を組み合わせる

動作環境

・macOS Sequoia (バージョン15.5)
・Python3 (3.10.9)
・Numpy (1.23.5) (数値計算用ライブラリ)
・Matplotlib (3.7.0) (アニメーション作成用ライブラリ)

順運動学

順運動学について説明する．
今回は下図のような3軸ロボットアームを考える．

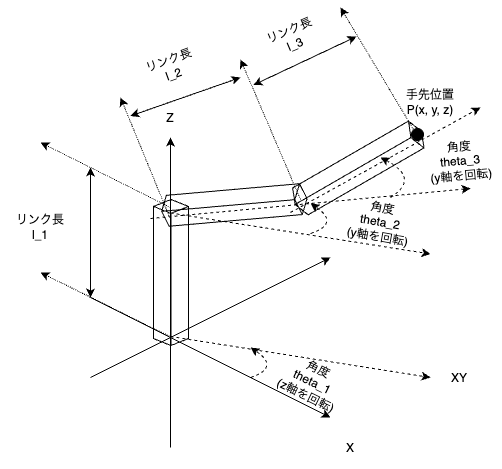
$l_{1}$はリンク1の長さ[m]，$l_{2}$はリンク2の長さ[m]，$l_{3}$はリンク3の長さ[m]です．
$\theta_{1}$は関節1の角度[rad]であり，z軸方向に回転する．
$\theta_{2}$は関節2の角度[rad]であり，y軸方向に回転する．
$\theta_{3}$は関節3の角度[rad]であり，y軸方向に回転する．
手先位置$P(x, y, z)$を各関節角度($\theta_{1}$，$\theta_{2}$, $\theta_{3}$)から計算する．

上図を一度下図のようにして考えてみる．(XY軸とZ軸を平面で表す)

はじめにリンク2の先端位置P2を計算する．
P2($xy_{2}, z_{2}$)は三角関数を使用することで，以下となる．

\displaylines{
xy_{2} = l_{2} * \cos\theta_{2} \\
 z_{2} = l_{1} + l_{2} * \sin\theta_{2} \\
}

次に手先位置Pを計算する．
P($xy, z$)は三角関数とP2($xy_{2}, z_{2}$)を使用することで，以下となる．

\displaylines{
xy = l_{2} * \cos\theta_{2} + l_{3} * \cos(\theta_{2} + \theta_{3}) \\
 z = l_{1} + l_{2} * \sin\theta_{2} + l_{3} * \sin(\theta_{2} + \theta_{3}) \\
}

次に，XY軸をX軸とY軸の平面で記載すると下図のようになる．

先ほどXY軸の位置を算出できたため，XY軸をX軸とY軸に分解することで，XとYを算出することが可能となる．
XとYは以下のように求まる．

\displaylines{
xy = l_{2} * \cos\theta_{2} + l_{3} * \cos(\theta_{2} + \theta_{3}) \\
 x = \cos\theta_{1} * xy = \cos\theta_{1} * (l_{2} * \cos\theta_{2} + l_{3} * \cos(\theta_{2} + \theta_{3}) ) \\
 y = \sin\theta_{1} * xy = \sin\theta_{1} * (l_{2} * \cos\theta_{2} + l_{3} * \cos(\theta_{2} + \theta_{3}) ) \\
}

順運動学によるロボットの手先位置

上記よりロボットの手先位置$P (x, y, z)$を計算したため，下記にまとめる．

\displaylines{
 x = \cos\theta_{1} * (l_{2} * \cos\theta_{2} + l_{3} * \cos(\theta_{2} + \theta_{3}) ) \\
 y = \sin\theta_{1} * (l_{2} * \cos\theta_{2} + l_{3} * \cos(\theta_{2} + \theta_{3}) ) \\
 z = l_{1} + l_{2} * \sin\theta_{2} + l_{3} * \sin(\theta_{2} + \theta_{3}) \\
}

順運動学のソースコード

定数を定義するファイル (constant.py)

定数を定義するファイルを下記に記す．

constant.py

# 複数ファイルで使用する定数の定義


# 次元数を定義
DIMENTION_NONE  = -1    # 未定義
DIMENTION_2D    =  2    # 2次元
DIMENTION_3D    =  3    # 3次元

# 回転軸
ROTATION_X_AXIS = "rot_x"   # x軸周りに回転
ROTATION_Y_AXIS = "rot_y"   # y軸周りに回転
ROTATION_Z_AXIS = "rot_z"   # z軸周りに回転

3軸ロボットアームを定義するファイル (robot.py)

3軸ロボットアームを定義するファイルを下記に記す．

robot.py

# ロボットアームの運動学を記載

# ライブラリの読み込み
import numpy as np

# 自作モジュールの読み込み
from constant import *              # 定数
from rotation import Rotation       # 回転行列


class Robot:
    """
    ロボットのベースクラス(抽象クラス)
    
    プロパティ
        _links(numpy.ndarray): ロボットのリンク長 [m]
        _rot(Rotation): 回転行列クラス
        _objects(list): 干渉物オブジェクト
        _manager(fcl.DynamicAABBTreeCollisionManager): 干渉判定クラス
    
    メソッド
        public
            forward_kinematics(): 順運動学 (ロボットの関節角度からロボットの手先位置を算出)
            inverse_kinematics(): 逆運動学 (ロボットの手先位置からロボットの関節角度を算出)
            forward_kinematics_all_pos(): 順運動学で全リンクの位置を取得
            update(): 角度を与えて，各リンクの直方体を更新する
            links(): _linksプロパティのゲッター
            manager(): _managerプロパティのゲッター
    """
    # 定数の定義
    _DIMENTION_POSE  = DIMENTION_NONE       # 手先位置の次元数
    _DIMENTION_THETA = DIMENTION_NONE       # 関節角度の次元数
    _DIMENTION_LINK  = DIMENTION_NONE       # リンク数
    _DIMENTION_AXIS  = DIMENTION_NONE       # 回転軸数
    
    _INITIAL_THETA   = 0.0                  # 初期回転角度 [rad]
    
    
    def __init__(self, links):
        """
        コンストラクタ

        パラメータ
            links(numpy.ndarray): ロボットのリンク長 [m]
        """
        if np.size(links) != self._DIMENTION_LINK:
            # 異常
            raise ValueError(f"links's size is abnormal. correct is {self._DIMENTION_Link}")

        # プロパティの初期化
        self._links = links
        self._rot = Rotation()
        self._objects = []
        self._manager = None

    @property
    def links(self):
        """
        _linksプロパティのゲッター
        """
        return self._links

    @property
    def manager(self):
        """
        _managerプロパティのゲッター
        """
        return self._manager

    def forward_kinematics(self, thetas):
        """
        順運動学 (ロボットの関節角度からロボットの手先位置を算出)

        パラメータ
            thetas(numpy.ndarray): ロボットの関節角度 [rad]
        
        戻り値
            pose(numpy.ndarray): ロボットの手先位置 (位置 + 姿勢) [m] + [rad]
        """
        raise NotImplementedError("forward_kinematics() is necessary override.")

    def inverse_kinematics(self, pose):
        """
        逆運動学 (ロボットの手先位置からロボットの関節角度を算出)

        パラメータ
            pose(numpy.ndarray): ロボットの手先位置 (位置 + 姿勢) [m] + [rad]
        
        戻り値
            thetas(numpy.ndarray): ロボットの関節角度 [rad]
        """
        raise NotImplementedError("inverse_kinematics() is necessary override.")

    def forward_kinematics_all_pos(self, thetas):
        """
        順運動学で全リンクの位置を取得

        パラメータ
            thetas(numpy.ndarray): ロボットの関節角度 [rad]
        
        戻り値
            all_pose(numpy.ndarray): ロボットの全リンク位置 (位置 + 姿勢) [m] + [rad]
        """
        raise NotImplementedError("forward_kinematics() is necessary override.")

    def update(self, thetas):
        """
        角度を与えて，各リンクの直方体を更新する

        パラメータ
            thetas(numpy.ndarray): ロボットの関節角度 [rad]
        """
        raise NotImplementedError("update() is necessary override.")


class Robot3DoF(Robot):
    """
    2軸ロボットクラス
    
    プロパティ
        _links(numpy.ndarray): ロボットのリンク長
        _rot(Rotation): 回転行列クラス
        _axiss(list): 関節の回転軸
    
    メソッド
        public
            forward_kinematics(): 順運動学 (ロボットの関節角度からロボットの手先位置を算出)
            inverse_kinematics(): 逆運動学 (ロボットの手先位置からロボットの関節角度を算出)
            forward_kinematics_all_pos(): 順運動学で全リンクの位置を取得
            update(): 角度を与えて，各リンクの直方体を更新する
    """
    # 定数の定義
    _DIMENTION_POSE  = DIMENTION_3D         # 手先位置の次元数
    _DIMENTION_THETA = DIMENTION_3D         # 関節角度の次元数
    _DIMENTION_LINK  = DIMENTION_3D         # リンク数
    
    
    def __init__(self, links):
        """
        コンストラクタ

        パラメータ
            links(numpy.ndarray): ロボットのリンク長 [m]
        """
        # 親クラスの初期化
        super().__init__(links)

    def forward_kinematics(self, thetas):
        """
        順運動学 (ロボットの関節角度からロボットの手先位置を算出)

        パラメータ
            thetas(numpy.ndarray): ロボットの関節角度 [rad]
        
        戻り値
            pose(numpy.ndarray): ロボットの手先位置 (位置) [m]
        """
        # パラメータの次元数を確認
        if np.size(thetas) != self._DIMENTION_THETA:
            raise ValueError(f"thetas's size is abnormal. thetas's size is {np.size(thetas)}")

        # あらかじめ三角関数を算出する
        sin1  = np.sin(thetas[0])
        sin2  = np.sin(thetas[1])
        sin23 = np.sin(thetas[1] + thetas[2])
        cos1  = np.cos(thetas[0])
        cos2  = np.cos(thetas[1])
        cos23 = np.cos(thetas[1] + thetas[2])

        # ロボットの手先位置を算出
        pxy_common = self._links[1] * cos2 + self._links[2] * cos23
        px = cos1 * pxy_common
        py = sin1 * pxy_common
        pz = self._links[0] + self._links[1] * sin2 + self._links[2] * sin23
        pose = np.array([px, py, pz])

        return pose

    def forward_kinematics_all_link_pos(self, thetas):
        """
        順運動学で全リンクの位置を取得 (グラフの描画で使用する)

        パラメータ
            thetas(numpy.ndarray): ロボットの関節角度 [rad]
        
        戻り値
            all_link_pose(numpy.ndarray): ロボットの全リンク位置 (位置 + 姿勢) [m] + [rad]
        """
        # パラメータの次元数を確認
        if np.size(thetas) != self._DIMENTION_THETA:
            raise ValueError(f"thetas's size is abnormal. thetas's size is {np.size(thetas)}")

        # 回転角度とリンク長をローカル変数に保存
        theta1 = thetas[0]
        theta2 = thetas[1]
        theta3 = thetas[2]
        link1  = self._links[0]
        link2  = self._links[1]
        link3  = self._links[2]

        # 三角関数を計算
        s1  = np.sin(theta1)
        c1  = np.cos(theta1)
        s2  = np.sin(theta2)
        c2  = np.cos(theta2)
        s3  = np.sin(theta3)
        c3  = np.cos(theta3)
        s12 = np.sin(theta1 + theta2)
        c12 = np.cos(theta1 + theta2)
        s23 = np.sin(theta2 + theta3)
        c23 = np.cos(theta2 + theta3)

        # 各リンクの位置を算出
        base_pos  = np.zeros(self._DIMENTION_POSE)
        link1_pos = np.array([0, 0, link1])
        link2_xy_common = link2 * c2
        link2_pos = np.array([c1 * link2_xy_common, s1 * link2_xy_common, link1 + link2 * s2])
        link3_xy_common = link2 * c2 + link3 * c23
        link3_pos = np.array([c1 * link3_xy_common, s1 * link3_xy_common, link1 + link2 * s2 + link3 * s23])

        # 全リンクの位置を算出
        all_link_pose = np.array([base_pos, link1_pos, link2_pos, link3_pos])

        return all_link_pose

メイン(プロットなど)処理 (main.py)

メイン処理ファイルを下記に記す．

main.py

# メイン処理

# ライブラリの読み込み
import numpy as np                  # 数値計算
import matplotlib.pyplot as plt     # 描画

# 自作モジュールの読み込み
from constant import *              # 定数
from robot import Robot3DoF         # ロボットクラス


LINE_WIDTH = 3                      # プロット時の線の太さ
GRAPH_FILE_NAME = "plot_3drob_forward_kinematics.png"


def main():
    """
    メイン処理
    """
    # 3軸ロボットのリンク長
    links = np.array([1.0, 1.0, 1.0])
    # 3軸ロボットのインスタンスを作成
    robot = Robot3DoF(links)

    # 関節角度 [deg] を定義
    deg_thetas = [0, 30, 60]
    # [deg]から[rad]へ変換
    candidate  = np.deg2rad(deg_thetas)
    all_thetas = np.array([[theta1, theta2, theta3] for theta1 in candidate for theta2 in candidate for theta3 in candidate])

    # 3次元グラフの作成
    fig = plt.figure()
    axis = fig.add_subplot(111, projection="3d")

    # 順運動学により，位置を算出
    for thetas in all_thetas:
        plot(robot, thetas, axis)

    # X軸，Y軸，Z軸の名称
    axis.set_xlabel("X [m]")
    axis.set_ylabel("Y [m]")
    axis.set_zlabel("Z [m]")

    axis.grid()
    axis.set_aspect("equal")
    plt.legend(fontsize=5, loc='center left', bbox_to_anchor=(0.8, .5))
    # # 凡例を見切れないようにするために，plt.tight_layout()
    plt.tight_layout()
    plt.savefig(GRAPH_FILE_NAME)
    plt.show()


def plot(robot, thetas, axis, label=True):
    """
    ロボットをプロット (将来的にはクラス化する)

    パラメータ
        robot(Robot3DoF): ロボット
        thetas(numpy.ndarray): 回転角度
        axis(figure.add_subplot): 3次元の描画軸
        label(bool): 描画時のラベルの有無
    """
    # 全リンクの位置を算出
    all_link_pos = robot.forward_kinematics_all_link_pos(thetas)

    # 線プロット
    if label:
        axis.plot(all_link_pos[:, 0], all_link_pos[:, 1], all_link_pos[:, 2], linewidth=LINE_WIDTH, label=f"theta1={np.rad2deg(thetas[0]):.1f} [deg], theta2={np.rad2deg(thetas[1]):.1f} [deg], theta3={np.rad2deg(thetas[2]):.1f} [deg]")
    else:
        axis.plot(all_link_pos[:, 0], all_link_pos[:, 1], all_link_pos[:, 2], linewidth=LINE_WIDTH)

    # 点プロット
    axis.scatter(all_link_pos[:, 0], all_link_pos[:, 1], all_link_pos[:, 2])


if __name__ == "__main__":
    # 本ファイルがメインで呼ばれた時の処理
    main()

処理結果

main.pyを実行し，順運動学が正しいかのグラフは下図である．

左下に判例を記載してある．グラフを見る限り，順運動学の処理は正常であることがわかる．

おわりに

本記事では，Pythonを使用して，下記内容を実装しました．
・3軸ロボットアームの順運動学 (順運動学 ... ロボットの関節角度からロボットの手先位置を算出する)

次記事では，下記内容を実装していきます．
・3軸ロボットアームの逆運動学 (逆運動学 ... ロボットの手先位置からロボットの関節角度を算出する)