はじめに
前回ロジスティック回帰の正則化のパラメーターについて調べた。
今回はその続きでsolver(最適化関数)について
前回 : https://qiita.com/hannnari0918/items/407e4fe6c0077e34ccab
公式doc solverの種類
solver : {‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}, default=’lbfgs’
Algorithm to use in the optimization problem.
- For small datasets, ‘liblinear’ is a good choice, whereas ‘sag’ and ‘saga’ are faster for large ones.
- For multiclass problems, only ‘newton-cg’, ‘sag’, ‘saga’ and ‘lbfgs’ handle multinomial loss; ‘liblinear’ is - limited to one-versus-rest schemes.
- ‘newton-cg’, ‘lbfgs’, ‘sag’ and ‘saga’ handle L2 or no penalty
- ‘liblinear’ and ‘saga’ also handle L1 penalty
- ‘saga’ also supports ‘elasticnet’ penalty
- ‘liblinear’ does not support setting penalty='none'
Note that ‘sag’ and ‘saga’ fast convergence is only guaranteed on features with approximately the same scale. You can preprocess the data with a scaler from sklearn.preprocessing.
| solver | 詳細 | 使用可能 |
|---|---|---|
| newton-cg | ニュートン共役勾配法 | L2, none |
| lbfgs | L-BFGS法 | L2, none |
| liblinear | liblinearというライブラリ 座標降下法 小さなデータセットだと早い |
L1, |
| sag(Stochastic Average Gradient ) | 確率勾配降下法(SAG)の進化系 大きなデータセットだと早い |
L2, none |
| saga | 確率勾配降下法(SAG)の進化系 大きなデータセットだと早い |
L1, L2, elasticnet, none |
Newton_cg(ニュートン共役勾配法)
ニュートン法について
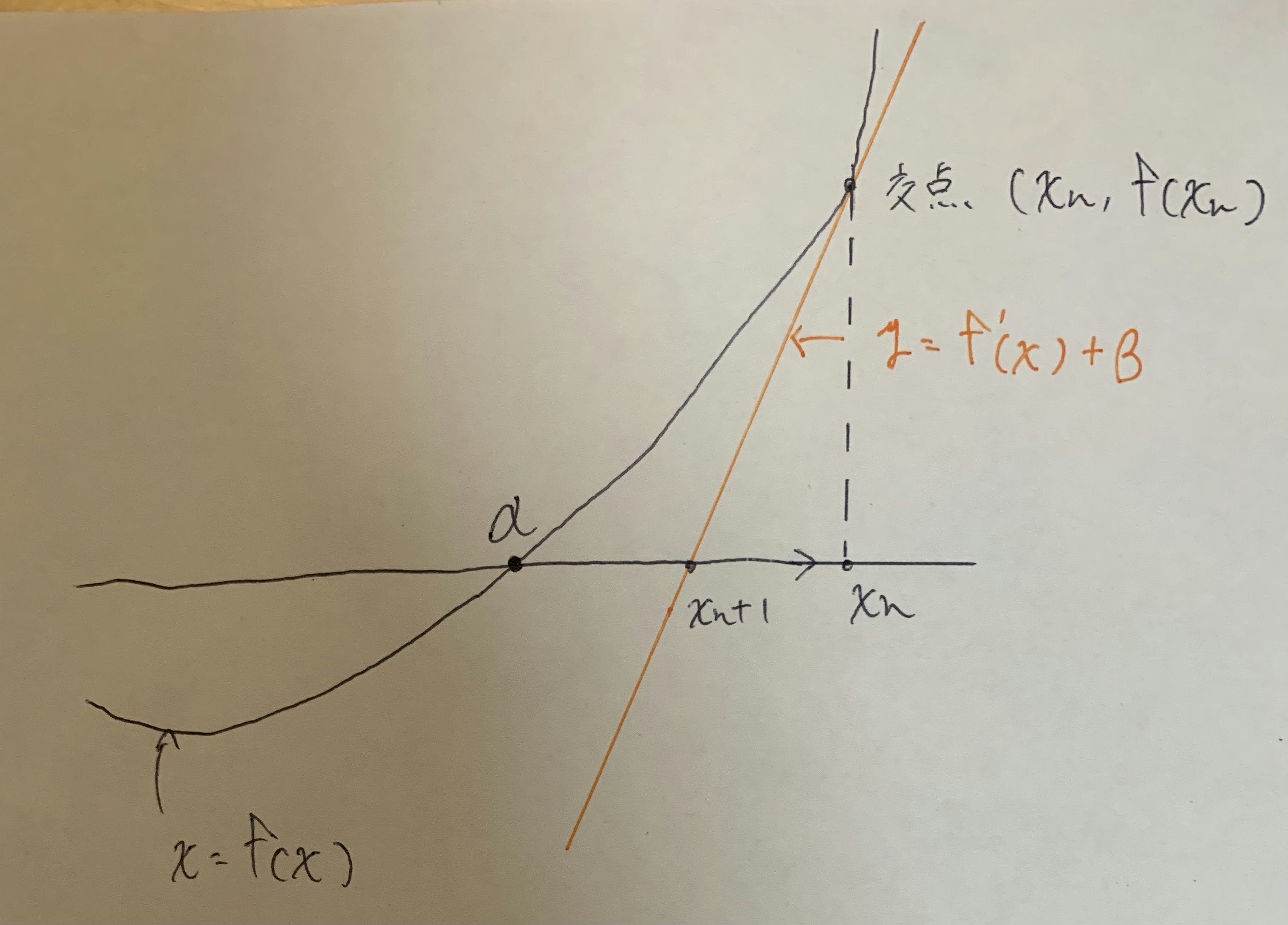
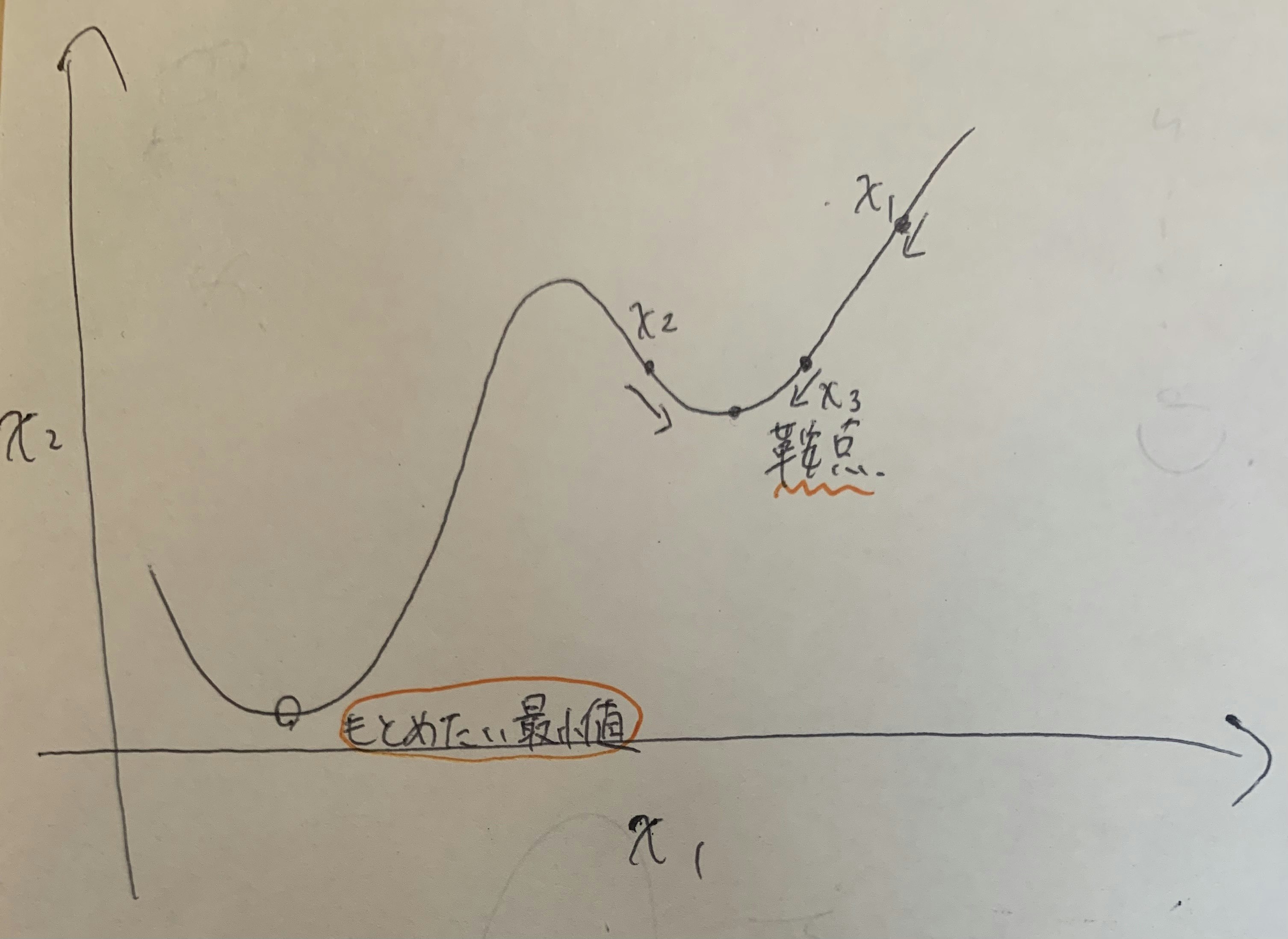
上記グラフの時x軸との交点αを求めたいという時に使うもの方法
最適化問題でグラフが複雑になったときにどんなグラフでも近似的に答えを見つけられるという関数
上記グラフの交点に対して接線の方程式を使い
$$y-f(x_n) = f'(x_n)(x-x_n)$$
が成立する。この式を式変形することで
$$x_{n+1}=x_n-\frac{f(x)}{f'(x)}$$
が成立し、この式はxだけで解けるので無限回行うことでαが求められるというもの。
共益勾配法について
この方の記事を参考にしてください : https://qiita.com/Dason08/items/27559e192a6a977dd5e5
イメージで言うと、勾配降下法で今いる地点の勾配から徐々にゴールを目指していたのを、ゴールへの向きを固定し勾配からベクトル力を決めてしまうというもの。
理論上、向きと力が100%あっていれば一発で最適化ができるよねっていう手法。
またずれていたとしても、その向きから垂直方向に調整を行うため一度調整したベクトルは変更されない。
(垂直ベクトルは0になるため)
ふたつを組み合わせると
ニュートン法や勾配降下法の弱点であった鞍点で止まってしまうことを防げるらしい
ベクトルでの調整になるのでL2ノルムでしか使えない。
lbfgs法
ニュートン法の弱点である微分をなくした最適化手法
メモリ(memoly)に優しくb,f,g,sパラメータを使うためこの名前が付けられている。
ニュートン法は次の値(n+1)を求めるののに微分を用いる。
微分によりヘッセ行列が作成される。
例えば
$$5x^2+3xy+6y^2=4$$
のヘッセ行列Hは(x^2,xy,y^2で微分)
$$
\begin{pmatrix}
10 & 3 \
3 & 12
\end{pmatrix}
$$
となる。この値が特徴量の2乗の値になるため、膨大なメモリを食ってしまうのを防ぐための手法。
ヘッセ行列を使わず、H^-1に近い行列Bを仮定し、この値を求めるやり方。
Bの求め方は省略するが、各方向への勾配gと移動量sを用いて算出できる。
またニュートン法のようにハイパーパラメータが存在せず、振動することがないのが特徴。
liblinear
オープンソースの機械学習ライブラリらしい。
公式https://www.csie.ntu.edu.tw/~cjlin/liblinear/
座標降下法をもちいてロジスティック回帰を行なっているものと、線形SVMをもちいて学習するものがある。
scikit-learnがどちらを使っているかは不明。
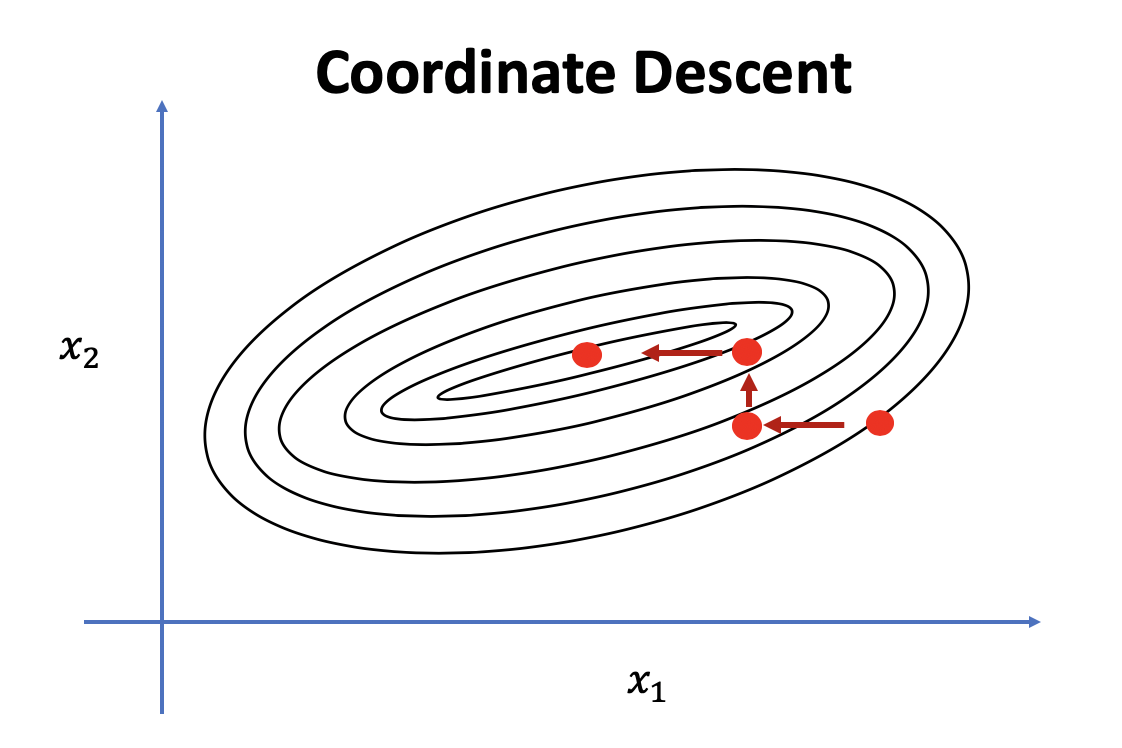
座標降下法について
イメージでいうと各特徴量にたいして順番に更新していく仕組み。
2次元だと考えると
$$x_1 , y_1 , x_2, y_2, x_3 ...$$
3次元ならば
$$x_1, y_1, z_1, x_2, y_2, z_2, x_3...$$
のように、求めたい変数以外を定数と仮定して解く方法。
メリット
- 特徴量を一つづつ更新していくため、メモリ容量に優しい。
- 超大規模データ等で使用できる
- 一度に更新するのは一つのパラメーターなので、そこまで計算に時間がかからないこと。
デメリット
- スパース問題(特徴がまんべんなくではなく、ある特徴量の比率が大きい)に使用できない。
- 最適解に精密さを必要と場合、使えない。
本題
公式docには小さなデータセットでいい選択だと記載されているため、SVMをもちいた最適化方法なのかもしれない。
他クラス分類には向かず、二値分類用に作成されている。そのため、非常に高速に学習する。
l2で使えないのはおそらくL1にしないと、そもそも超平面が作成されないから。
(L2だと合計ベクトルになるため)
noneで使用できない理由はわからない笑
SAG,SAGAについて
SGD確率的勾配降下法の進化系
ではSGDとはなんぞやという話になるので...
最急降下法
ロジスティック回帰のときに記載した、損失関数を少なくする方法の一つ。
元祖最適化関数といったイメージ。
何をしているかというと、今いる地点の勾配を求めそれを元にして次の地点に進む方法。
2次元で考えた場合、1000個のデータセットがあった場合全てを用いて各次元に対する重みを決定する。
特徴として、
- 全部のデータを用いて計算するため、パラレルで計算が可能
- 重みは決めれるが、下がるか上がるかは微分によって決まる。
- どれくらい下がるかはハイパーパラメータ
欠点として、全ての特徴量とデータを用いて計算を行うため時間がかかることと鞍点から脱出できないことが挙げられる。
(イメージでいうと全てのデータを用いるので優秀なベクトルが定められるので、幸か不幸か収束早く大きく動かない)
SGD(確率的勾配降下法)
最急降下法の後続としてできた最適化手法。
最急降下法がなんぞやとなるので唐突に上で説明した通り。
SGDがなにをしているかというと、最急降下法が全てのデータを用いてベクトルを決めていたのに対してランダムに選ばれた一つのデータを使ってベクトルを決めてしまうやり方。
はじめて聞いたとき劣化版にしか聞こえない
全データで学んだ方が確実に効率的なのに、なぜわざわざ1データのみでデータに寄与する変な方向のベクトルを見つけるのか。
変な方向のベクトルを使いたいから!
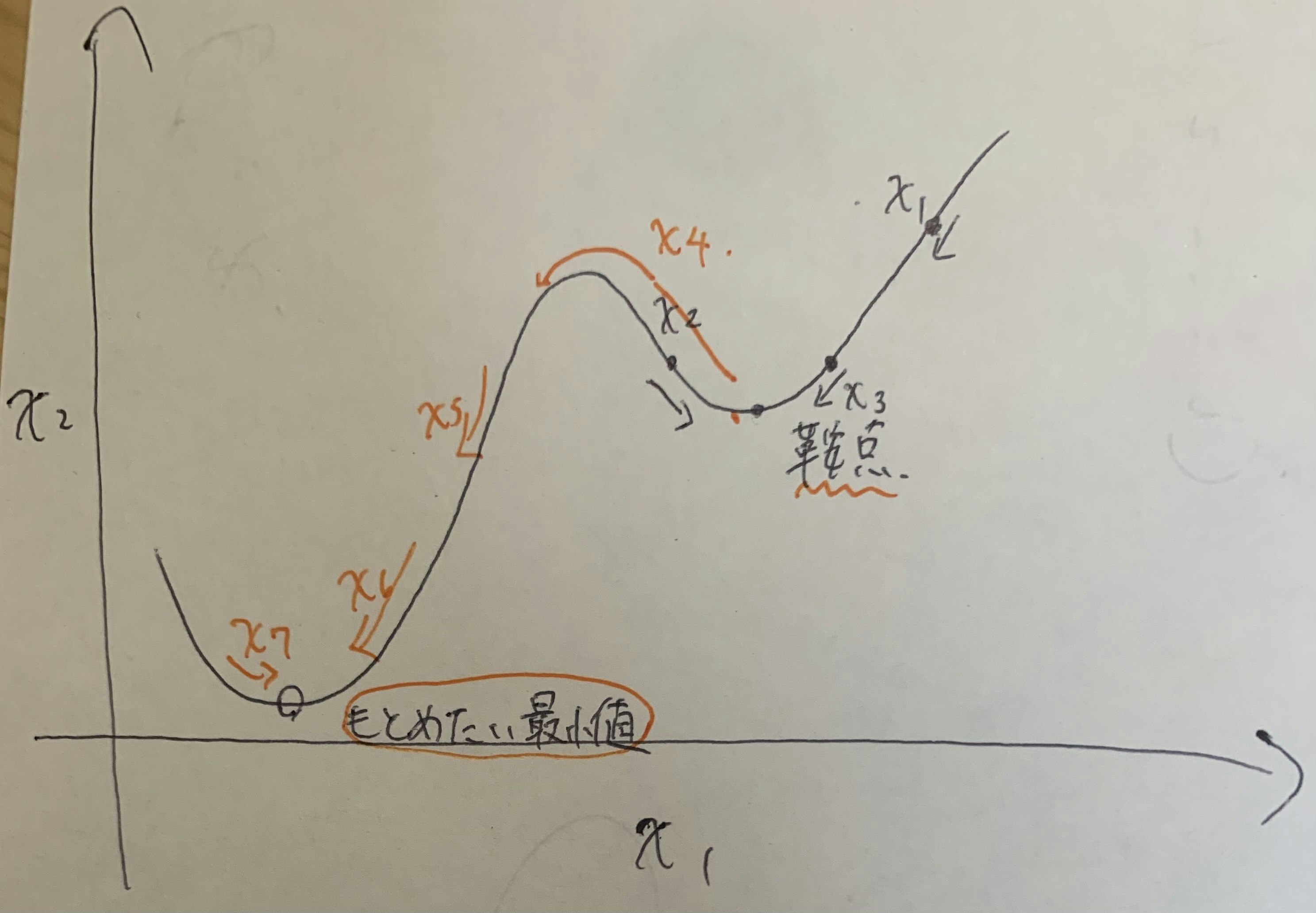
なぜそんなことをするのかというと、先の述べた鞍点の問題を解決してくれるからである。
詳しくいうと
全部のデータを用いた最高の学習方法では鞍点から抜けれなくなったのをその変なむきのベクトルを使うことで脱出できるからという理由である。
SAG
sag(Stochastic Average Gradient)という名前の通り、平均をとって勾配を決めるやり方。
根本的にはSGDとやり方は変わらないが、今までの計算してきた回数と勾配を保存しておき無限回行うことで最急降下法と同じように前データで勾配計算を行う手法となる。
勾配計算を行うやり方が一括ではなく、ランダムな順序のデータで学習するので鞍点に陥らなくて済むよね!といった話である。
勾配平均の求め方は
$$\bar{w_n} = \frac{1}{n}\sum_{n}{w_t}$$
n+1(データを一つ加えた勾配)
$$\bar{w_{n+1}} = \frac{n}{n+1}\bar{w_t} + \frac{1}{n+1}w_{t+1}$$
以上の式で求められる。
自分の感覚だとnが十分に大きくなるとほぼほぼ更新されないので、鞍点から抜け出せるかは運か反転回数が大事になってきそうに見える。
SAGA
SAGとほぼほぼ変わらないが平均を取らない計算方法になる
nで割らない計算式
(https://www.msi.co.jp/nuopt/glossary/term_da265770bed70e5f0a764f3d20c0ce3d242e6467.html)[https://www.msi.co.jp/nuopt/glossary/term_da265770bed70e5f0a764f3d20c0ce3d242e6467.html]
終わりに
手法をなんとなくだが、イメージできるようになった。
自分が思い返したときにわかりやすいように記載しただけなので、他人がみても多分わからないと思われる笑
まだまだ信じられないくらいの量の最適化手法ががあるので、暇があれば探していきたい。