意外とネット上で探しても出てこなかったので、頑張って導出してみようと思います。
2次曲線の式っていうのは$ax^2+bxy+cy^2+dx+ey+f=0$みたいな2次関数のことです。
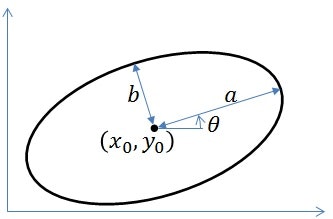
楕円パラメータっていうのは楕円中心$(x_0,y_0)$、X軸方向半径$a$、Y軸方向半径$b$、回転$\theta$のことのつもりです。
媒介変数とかのことではありません。
2次曲線の式
2次曲線の式は以下の数式で表現することにします。
\left[\begin{array}{c} x & y & f_0 \end{array}\right]
\left[\begin{array}{c} A&B&D\\B&C&E\\D&E&F \end{array}\right]
\left[\begin{array}{c}x\\y\\f_0\end{array}\right]
= Ax^2+2Bxy+Cy^2+2Dxf_0+2Eyf_0+Ff_0^2=0
この$f_0$ってのは見慣れないかと思いますが、各項の次元をそろえるための定数です。数値計算的には適当な値に設定することで計算の精度を保つことができます($F$だけめっちゃ大きくなるみたいなのを防げる)。
基本的には$f_0=1$と考えちゃっていいです。
参考- http://www.iim.cs.tut.ac.jp/~kanatani/papers/newlsellipse.pdf
結論
先に結論から述べると、
\begin{eqnarray}
x_0 &=& \frac{BE-CD}{AC-B^2}f0 \\
y_0 &=& \frac{BD-AE}{AC-B^2}f0 \\
a^2 &=&\frac{2\left(\left(CD-BE\right)D + \left(AE-BD\right)E - (AC-B^2)F\right)}{(AC-B^2)\left(A+C+\sqrt{(A-C)^2+4B^2}\right)}f_0^2 &=& -2f_0\frac{Dx_0+Ey_0+Ff_0}{A+C+\sqrt{(A-C)^2+4B^2}} \\
b^2 &=&\frac{2\left(\left(CD-BE\right)D + \left(AE-BD\right)E - (AC-B^2)F\right)}{(AC-B^2)\left(A+C-\sqrt{(A-C)^2+4B^2}\right)}f_0^2 &=& -2f_0\frac{Dx_0+Ey_0+Ff_0}{A+C-\sqrt{(A-C)^2+4B^2}} \\
\theta &=& \frac{1}{2}\tan^{-1}\frac{2B}{A-C}
\end{eqnarray}
となります。
以下頑張って導出していきます。
楕円の方程式
楕円の方程式ですが、基本的な楕円の方程式$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$を回転&平行移動させて
\left(\frac{\left(x-x_0\right)\cos\theta + \left(y-y_0\right)\sin\theta}{a}\right)^2 + \left(\frac{-\left(x-x_0\right)\sin\theta + \left(y-y_0\right)\cos\theta}{b}\right)^2 = 1
となり、これを$x,y$に関して整理して
\begin{eqnarray}
&&\left(\frac{1}{a^2}\cos^2\theta+\frac{1}{b^2}\sin^2\theta\right)x^2 \\
&+&2\left(\frac{1}{a^2}-\frac{1}{b^2}\right)\sin\theta \cos\theta xy \\
&+&\left(\frac{1}{a^2}\sin^2\theta+\frac{1}{b^2}\cos^2\theta\right)y^2 \\
&-&2\left(\frac{1}{a^2}\cos\theta\left(x_0\cos\theta + y_0\sin\theta\right) - \frac{1}{b^2}\sin\theta\left(-x_0\sin\theta + y_0\cos\theta\right)\right)x \\
&-&2\left(\frac{1}{a^2}\sin\theta\left(x_0\cos\theta + y_0\sin\theta\right) + \frac{1}{b^2}\cos\theta\left(-x_0\sin\theta + y_0\cos\theta\right)\right)y \\
&+&\frac{1}{a^2}\left(x_0\cos\theta + y_0\sin\theta\right)^2 + \frac{1}{b^2}\left(-x_0\sin\theta + y_0\cos\theta\right)^2 - 1 \\
&=&0
\end{eqnarray}
となります。
両式の比較
2次曲線の式と楕円の方程式を比較して、2次曲線の式の各パラメータにはスケールの自由度があることを考えると
\begin{eqnarray}
At &=& \frac{1}{a^2}\cos^2\theta+\frac{1}{b^2}\sin^2\theta \\
Bt &=& \left(\frac{1}{a^2}-\frac{1}{b^2}\right)\sin\theta \cos\theta \\
Ct &=& \frac{1}{a^2}\sin^2\theta+\frac{1}{b^2}\cos^2\theta \\
Dt &=& -\frac{1}{f_0}\left(\frac{1}{a^2}\cos\theta\left(x_0\cos\theta + y_0\sin\theta\right) - \frac{1}{b^2}\sin\theta\left(-x_0\sin\theta + y_0\cos\theta\right)\right) \\
Et &=& -\frac{1}{f_0}\left(\frac{1}{a^2}\sin\theta\left(x_0\cos\theta + y_0\sin\theta\right) + \frac{1}{b^2}\cos\theta\left(-x_0\sin\theta + y_0\cos\theta\right)\right) \\
Ft &=& \frac{1}{f_0^2}\left(\frac{1}{a^2}\left(x_0\cos\theta + y_0\sin\theta\right)^2 + \frac{1}{b^2}\left(-x_0\sin\theta + y_0\cos\theta\right)^2 - 1\right)
\end{eqnarray}
ここで、$t$はスケール方向の自由度です。
楕円パラメータの導出
まず$A$と$C$の式の差をとって
\begin{eqnarray}
At-Ct &=& \frac{1}{a^2}\left(\cos^2\theta-\sin^2\theta\right) + \frac{1}{b^2}\left(\sin^2\theta-\cos^2\theta\right) \\
(A-C)t &=& \left(\frac{1}{a^2}-\frac{1}{b^2}\right)\left(\cos^2\theta-\sin^2\theta\right) \\
\frac{1}{a^2}-\frac{1}{b^2} &=& \frac{A-C}{\cos^2\theta-\sin^2\theta}t
\end{eqnarray}
$B$の式に代入して
\begin{eqnarray}
Bt &=& (A-C)\frac{\sin\theta \cos\theta}{\cos^2\theta - \sin^2\theta}t \\
B &=& (A-C)\frac{1}{2}\frac{\sin2\theta}{\cos2\theta} \because 半角公式 \\
\tan2\theta &=& \frac{2B}{A-C} \\
\theta &=& \frac{1}{2}\tan^{-1}\frac{2B}{A-C}
\end{eqnarray}
となり$\theta$が求められました。
次に$D$と$E$の式を使って$\frac{1}{b^2}$を消去します。
\begin{eqnarray}
Dt\cos\theta + Et\sin\theta = -\frac{1}{f_0a^2}\left(x_0\cos\theta + y_0\sin\theta\right)
\end{eqnarray}
同様に$\frac{1}{a^2}$を消去します。
\begin{eqnarray}
-Dt\sin\theta + Et\cos\theta = -\frac{1}{f_0b^2}\left(-x_0\sin\theta + y_0\cos\theta\right)
\end{eqnarray}
この2式から$E$の項を消去して
\begin{eqnarray}
\left(Dt\cos\theta + Et\sin\theta\right)\cos\theta - \left(-Dt\sin\theta + Et\cos\theta\right)\sin\theta &=&
-\frac{1}{f_0}\left(\frac{1}{a^2}\left(x_0\cos\theta + y_0\sin\theta\right)\cos\theta
- \frac{1}{b^2}\left(-x_0\sin\theta + y_0\cos\theta\right)\sin\theta\right)\\
Dt\left(\cos^2\theta + \sin^2\theta\right) &=&
-\frac{1}{f_0}\left(\left(\frac{1}{a^2}\cos^2\theta+\frac{1}{b^2}\sin^2\theta\right)x_0
+ \left(\frac{1}{a^2}-\frac{1}{b^2}\right)\sin\theta \cos\theta y_0\right) \\
Dt &=& -\frac{1}{f_0}\left(Atx_0 + Bty_0\right) \\
Ax_0 + By_0 &=& -Df_0
\end{eqnarray}
同様に
\begin{eqnarray}
\left(Dt\cos\theta + Et\sin\theta\right)\sin\theta + \left(-Dt\sin\theta + Et\cos\theta\right)\cos\theta &=&
-\frac{1}{f_0}\left(\frac{1}{a^2}\left(x_0\cos\theta + y_0\sin\theta\right)\sin\theta
+ \frac{1}{b^2}\left(-x_0\sin\theta + y_0\cos\theta\right)\cos\theta\right)\\
Et\left(\sin^2\theta + \cos^2\theta\right) &=&
-\frac{1}{f_0}\left(\left(\frac{1}{a^2}-\frac{1}{b^2}\right)\sin\theta \cos\theta x_0
+ \left(\frac{1}{a^2}\sin^2\theta+\frac{1}{b^2}\cos^2\theta\right)y_0\right) \\
Et&=& -\frac{1}{f_0}\left(Btx_0 + Cty_0\right) \\
Bx_0 + Cy_0 &=& -Ef_0
\end{eqnarray}
連立方程式
\begin{eqnarray}
Ax_0 + By_0 &=& -Df_0 \\
Bx_0 + Cy_0 &=& -Ef_0
\end{eqnarray}
を解いて
\begin{eqnarray}
x_0 &=& \frac{BE-CD}{AC-B^2}f0 \\
y_0 &=& \frac{BD-AE}{AC-B^2}f0
\end{eqnarray}
となり、楕円中心$x_0,y_0$を求められました。
$A$と$C$の式を変形して$\frac{1}{b^2}$の項を消去すると
\begin{eqnarray}
At\cos^2\theta - Ct\sin^2\theta &=& \frac{1}{a^2}\left(\cos^4\theta - \sin^4\theta\right) \\
\left(A\cos^2\theta - C\sin^2\theta\right)t &=&
\frac{1}{a^2}\left(\cos^2\theta - \sin^2\theta\right)\left(\cos^2\theta + \sin^2\theta\right) \\
\left(A\cos^2\theta - C\sin^2\theta\right)t &=& \frac{1}{a^2}\left(\cos^2\theta - \sin^2\theta\right) \\
\frac{1}{a^2} &=& \frac{A\cos^2\theta - C\sin^2\theta}{\cos^2\theta - \sin^2\theta}t
\end{eqnarray}
となり、同様に
\begin{eqnarray}
\frac{1}{b^2} &=& \frac{A\sin^2\theta - C\cos^2\theta}{\sin^2\theta - \cos^2\theta}t
\end{eqnarray}
また、$F$の式から$t$を求めると
\begin{eqnarray}
t &=& \frac{1}{Ff_0^2}\left(\frac{1}{a^2}\left(x_0\cos\theta + y_0\sin\theta\right)^2 + \frac{1}{b^2}\left(-x_0\sin\theta + y_0\cos\theta\right)^2 - 1 \right) \\
&=& \frac{1}{Ff_0^2}\left(\frac{X^2}{a^2} + \frac{Y^2}{b^2} - 1\right)
\end{eqnarray}
となります。ただし$X=x_0\cos\theta + y_0\sin\theta, Y=-x_0\sin\theta + y_0\cos\theta$としました。これを上の$\frac{1}{a^2},\frac{1}{b^2}$の式に代入して
\begin{eqnarray}
\frac{1}{a^2} &=& \frac{A\cos^2\theta - C\sin^2\theta}{\left(\cos^2\theta - \sin^2\theta\right)Ff_0^2}\left(\frac{X^2}{a^2} + \frac{Y^2}{b^2} - 1\right)
= k_1\left(\frac{X^2}{a^2} + \frac{Y^2}{b^2} - 1\right) \\
\frac{1}{a^2} &=& \frac{A\sin^2\theta - C\cos^2\theta}{\left(\sin^2\theta - \cos^2\theta\right)Ff_0^2}\left(\frac{X^2}{a^2} + \frac{Y^2}{b^2} - 1\right)
= k_2\left(\frac{X^2}{a^2} + \frac{Y^2}{b^2} - 1\right)
\end{eqnarray}
となり、この連立方程式を$a^2,b^2$について解くと
\begin{eqnarray}
a^2 &=& \frac{k_1X^2 + k_2Y^2 - 1}{k_1} \\
b^2 &=& \frac{k_1X^2 + k_2Y^2 - 1}{k_2}
\end{eqnarray}
ただしここで、
\begin{eqnarray}
k_1 &=& \frac{A\cos^2\theta - C\sin^2\theta}{\left(\cos^2\theta - \sin^2\theta\right)Ff_0^2} \\
&=& \frac{\frac{1+\cos2\theta}{2}A - \frac{1-\cos2\theta}{2}C}{\frac{1+\cos2\theta}{2} - \frac{1-\cos2\theta}{2}}\frac{1}{Ff_0^2} \because 半角公式\\
&=& \frac{A-C + (A+C)\cos2\theta}{2Ff_0^2\cos2\theta}
\end{eqnarray}
同様に
\begin{eqnarray}
k_2 = \frac{C-A + (A+C)\cos2\theta}{2Ff_0^2\cos2\theta}
\end{eqnarray}
です。
ここで、
\begin{eqnarray}
X &=& \left(x_0\cos\theta + y_0\sin\theta\right)^2 \\
&=& x_0^2\cos^2\theta + 2x_0y_0\sin\theta\cos\theta + y_0^2\sin^2\theta \\
&=& \frac{1}{2}\left(x_0^2\left(1+\cos2\theta\right) + 2x_0y_0\sin2\theta + y_0^2\left(1-\cos2\theta\right)\right) \\
Y &=& \left(-x_0\sin\theta + y_0\cos\theta\right)^2 \\
&=& x_0^2\sin^2\theta - 2x_0y_0\sin\theta\cos\theta + y_0^2\cos^2\theta \\
&=& \frac{1}{2}\left(x_0^2\left(1-\cos2\theta\right) - 2x_0y_0\sin2\theta + y_0^2\left(1+\cos2\theta\right)\right)
\end{eqnarray}
と$k_1,k_2$を代入してまとめると
\begin{eqnarray}
a^2 &=& \frac{2\left(Ax_0^2\cos2\theta + (A-C)x_0y_0\sin2\theta + Cy_0^2\cos2\theta -Ff_0^2\cos2\theta\right)}{A-C+(A+C)\cos2\theta} \\
&=& \frac
{2\left(A(A-C)x_0^2 + 2B(A-C)x_0y_0 + C(A-C)y_0^2 - F(A-C)f_0^2\right)}
{(A-C)\sqrt{(A-C)^2+4B^2} + (A+C)(A-C)} \\
&& \because \tan2\theta = \frac{2B}{A-C} \Rightarrow \sin2\theta = \frac{2B}{\sqrt{(A-C)^2+4B^2}}, \cos2\theta = \frac{A-C}{\sqrt{(A-C)^2+4B^2}} \\
&=&\frac{2\left(Ax_0^2 + 2Bx_0y_0 + Cy_0^2 - Ff_0^2\right)}{A+C+\sqrt{(A-C)^2+4B^2}}
\end{eqnarray}
同様に
\begin{eqnarray}
b^2 =\frac{2\left(Ax_0^2 + 2Bx_0y_0 + Cy_0^2 - Ff_0^2\right)}{A+C-\sqrt{(A-C)^2+4B^2}}
\end{eqnarray}
となります。
$x_0 = \frac{BE-CD}{AC-B^2}f0, y_0 = \frac{BD-AE}{AC-B^2}f0$だったので、これを代入してまとめると
\begin{eqnarray}
a^2 &=&\frac
{2\left(\left(CD-BE\right)D + \left(AE-BD\right)E - (AC-B^2)F\right)}
{(AC-B^2)\left(A+C+\sqrt{(A-C)^2+4B^2}\right)}f_0^2 \\
b^2 &=&\frac
{2\left(\left(CD-BE\right)D + \left(AE-BD\right)E - (AC-B^2)F\right)}
{(AC-B^2)\left(A+C-\sqrt{(A-C)^2+4B^2}\right)}f_0^2
\end{eqnarray}
となり、楕円の径$a,b$を求められます。
まとめ
最後にもう一度まとめると、
\begin{eqnarray}
x_0 &=& \frac{BE-CD}{AC-B^2}f0 \\
y_0 &=& \frac{BD-AE}{AC-B^2}f0 \\
a^2 &=&\frac{2\left(\left(CD-BE\right)D + \left(AE-BD\right)E - (AC-B^2)F\right)}{(AC-B^2)\left(A+C+\sqrt{(A-C)^2+4B^2}\right)}f_0^2 &=& -2f_0\frac{Dx_0+Ey_0+Ff_0}{A+C+\sqrt{(A-C)^2+4B^2}} \\
b^2 &=&\frac{2\left(\left(CD-BE\right)D + \left(AE-BD\right)E - (AC-B^2)F\right)}{(AC-B^2)\left(A+C-\sqrt{(A-C)^2+4B^2}\right)}f_0^2 &=& -2f_0\frac{Dx_0+Ey_0+Ff_0}{A+C-\sqrt{(A-C)^2+4B^2}} \\
\theta &=& \frac{1}{2}\tan^{-1}\frac{2B}{A-C}
\end{eqnarray}
となります。
感想
とけてよかったとおもいました。
2次方程式が楕円でないときは$a^2$や$b^2$がマイナスになって$a,b$を実数で求められなくなったり、$AC-B^2$が$0$になって$x_0,y_0$が求められなくなったりするみたいです。$a,b$の式はなんかもうちょっと簡単になりそうですが私にはこれが限界でした。楕円の判別は$AC-B^2>0$なので、$AC-B^2>0$で2次曲線が図形になるなら$a^2,b^2>0$になると思うんですが、そのへんの証明もちょっと出来ませんでした。でもまぁ一応は楕円パラメータを求めることが出来たので良かったです。
それではさようなら。