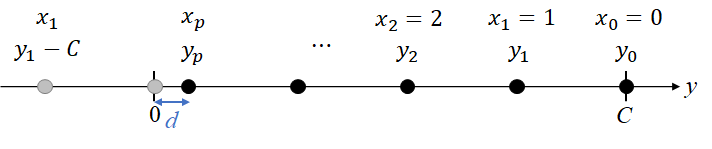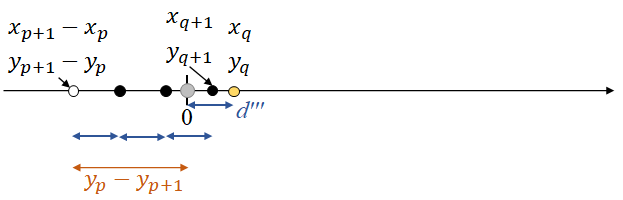問題文:AtCoder Grand Contest 045 F - Division into Multiples
よいグループになるA,Bの個数を求める
まず、よいグループになるときの$A$の個数$x$、$B$の個数$y$の組$(x,y)$を網羅することを考える。
求めるべき(x,y)の要件
以下の式を満たす組$(x,y)$を全て求めたい。
xA + yB \equiv 0 \pmod C \ \ \ \ \ \ \dots式(1)
ただし、最終目的がグループ数最大化なので、他の組より$x$も$y$も大きいような組は不要。つまり、$x$を昇順に並べると$y$が降順に並ぶように網羅する。
準備
まず、$A,B,C$の3つに共通の最大公約数で、$A,B,C$を割っておく。そうしても、$(x,y)$の組は変わらない。
更に、自分は気づかなかったが、$A,C$の最大公約数$g$で、$A$と$C$と$Y$を割っておくこともできる($Y$は割り切れなくても切り捨ててよい)。なぜなら、$B$と$g$は互いに素であるため($B$は既に$A,B,C$の共通の最大公約数で割ってあるので)、式(1)より、$y$が$g$で割り切れるはずである。そのため、$A$と$C$を$g$で割ってから求めた組$(x,y)$は、$g$で割らずに求めた組$(x,y)$に比べて$y$が$1/g$倍になっている。よって、$Y$を$g$で割っておけば、作れるよいグループ数が同じになる。
$g$で割らなくても解くことはできるが、説明が簡単になるので以下割ってあるものとする。同様に、$B,C$の最大公約数$g'$で$B$と$C$と$X$を割っておく。以上により、$A$と$C$は互いに素、$B$と$C$は互いに素になる。
基本アルゴリズム
組$(x,y)$には、以下の2つの性質がある。
- 性質1
- 組$(x,y)$が1つ求まったとする。すると、$x$と$y$を共に2倍、3倍、…してできる組$(kx,ky)$ $(k\ge 2)$も式(1)を満たす。但しこのままでは元の組$(x,y)$より大きいので不要な組。
- 性質2
- 組$(x,y)$の$y$が$C$以上なら、$C$を引いたもの$(x,y-C)$も条件を満たす。$x$についても同じ。
この2つの性質を利用し、次のようにして、$x$昇順&$y$降順な網羅をするアルゴリズムを考えることができる:
まず、$(x=0,y=C)$は解。次に、$x=1$のときの$y$を求める。$\pmod C$での割り算を使えば簡単に求まる。
\begin{align}
A+yB&\equiv 0 &\pmod C \\
y &\equiv -A/B &\pmod C
\end{align}
この$(x=1,y)$を種にして、$2$倍~$C$倍まで順に試すことを考える。$y$が$C$以上になったら常に$C$を引くものとする。すると、$y$が今までのどの$y$よりも小さい場合だけ採用していけば、$x$が昇順、$y$が降順に並ぶように組$(x,y)$を網羅できる1。
高速化
上記を愚直に実行すると計算量が$O(C)$になり、間に合わない。うまくスキップする方法を考える。
$x$昇順&$y$降順に並んだ組$(x,y)$を$(x_i,y_i)$とする。下図は、横方向に$y$の値を取り、$(x_0=0,y_0=C),$ $(x_1=1,y_1)$の$y_0$と$y_1$をプロットしたものである。また、$\pmod C$で同じになる値を同一視し、負の方にもプロットする。
ここに、$(x_1,y_1)$を$k$倍$(k=2,\dots,C)$したもの($C$を超えたら$C$を引く)を順にプロットしていくことを考える。下図のように、$y_0-y_1$間の距離と同じ幅で、$2$倍、$3$倍、… がプロットされ、それがそのまま$(x_2,y_2),$ $(x_3,y_3),$ $\dots$になる。$0$をまたぐ直前まで同様に続く。$0$をまたぐ直前を$(x_p,y_p)$とする。$y_1$が$C/2$以下の場合は、$(x_p,y_p)$ $=(x_1,y_1)$ になる。$0$と$y_p$の間の距離を$d$ $(=y_p)$とする。
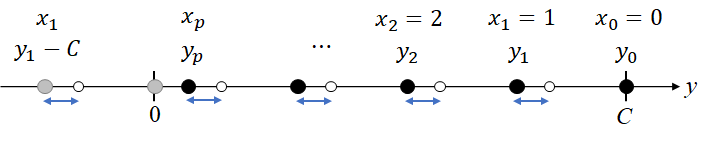
更に$k$を$1$ずつ増やしていくと、今度は$y_1$から$d$離れた場所、$y_2$から$d$離れた場所、…、というように、順にプロットされていく。
これを繰り返し、次に$x$昇順&$y$降順となる点が出現するのは、つまり次に$0$~$y_p$の間にプロットされるのは、$(x_1,y_1)$の負側の点から$d$ずつ刻んでいき、$0$を超えた瞬間である。
よって、刻む回数を$t$とすると、
\begin{align}
t &= \lceil (y_0-y_1)/d \rceil \\
x_{p+1} &= t*x_p + x_1 \\
y_{p+1} &= t*y_p + (y_1-C)
\end{align}
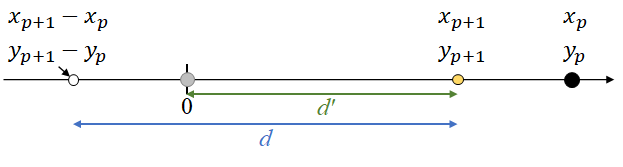
$(x_{p+1},y_{p+1})$が決まる周辺を拡大したものが下図である。$d$進むと、$x$が$x_p$増え、$y$が$y_p$増える。よって、$d$進んで$(x_{p+1},y_{p+1})$に到達する際の手前の点は、$(x=x_{p+1}-x_p,$ $y=y_{p+1}-y_p)$である。そして、その2つの点が、この時点で正負それぞれの方向で$0$に最も近い2点である。$0$と$y_{p+1}$の間の距離を$d'$ $(=y_{p+1})$とする。
この後、$k$を$1$ずつ増やしていくと、$x=1$のときの点から$d'$離れた場所、$x=2$のときの点から$d'$離れた場所、…、というように、既出の点から$d'$離れたところに必ずプロットされていく。よって、次に$x$昇順&$y$降順となる点が出現するのは、つまり次に$0$~$y_{p+1}$の間にプロットされるのは、下図のように、$(x=x_{p+1}-x_p,$ $y=y_{p+1}-y_p)$から$d'$離れた場所にプロットされるとき2。よって、
x_{p+2} = x_{p+1}-x_p + x_{p+1} = 2x_{p+1}-x_p \\
y_{p+2} = y_{p+1}-y_p + y_{p+1} = 2y_{p+1}-y_p
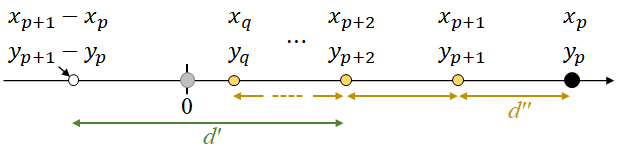
これは、$(x_p,y_p)$と$(x_{p+1},y_{p+1})$の間の距離$d''$で、等間隔に刻んでいくと見なすこともできる。これが$0$をまたぐ直前まで同様に続く。$0$をまたぐ直前を$(x_q,y_q)$とする。
同様の議論を繰り返すことで、$(x_{q+1},y_{q+1})$は、下図のとおり$d'''$を取ると、$(x_{p+1}-x_p,$ $y_{p+1}-y_p)$から$d'''$ずつ刻んで$0$を超えた瞬間の点なので、以下の計算で求まることが分かる。
\begin{align}
d''' &= y_q \\
t &= \lceil (y_p-y_{p+1})/d''' \rceil \\
x_{q+1} &= t*x_q + (x_{p+1}-x_p) \\
y_{q+1} &= t*y_q + (y_{p+1}-y_p)
\end{align}
以上を再帰的に繰り返し、$(x=C,y=0)$にたどり着いたら終了である。ただし、後述するとおり、途中で最適解を決定できるので、最後まで計算する必要はない。
また、$(x_p,y_p)$から$(x_q,y_q)$まで$d''$ずつ刻み続ける処理は、最大で$10^9$回程度繰り返す可能性があるので、実際には$(x_p,y_p)$と$(x_{p+1},y_{p+1})$と刻む回数$s$だけを持っておく。
よいグループが何個選べるか求める
問題設定
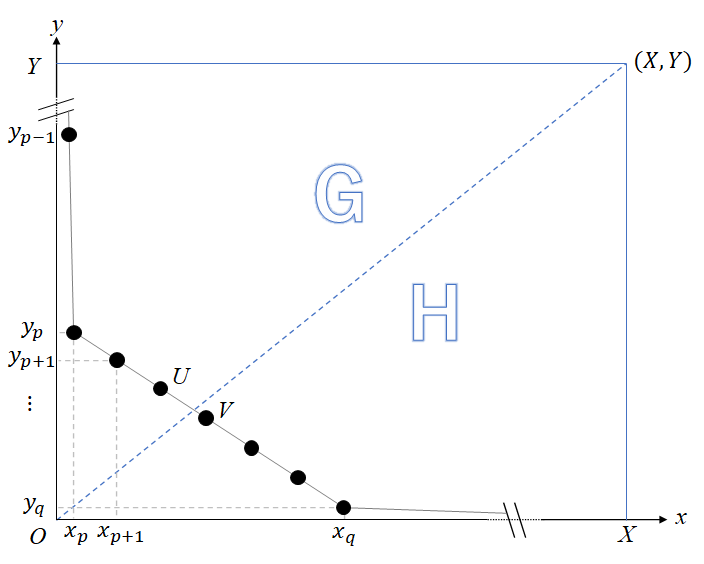
次に、$x$の合計が$X$以内、$y$の合計が$Y$以内になる制約の中で、求めた組$(x_i,y_i)$から重複を許して最大何個選べるかを考える。下図は、横軸$x$、縦軸$y$の二次元平面に組$(x_i,y_i)$をプロットしたものである。前述した、等間隔に並ぶ$(x_p,y_p),$ $(x_{p+1},y_{p+1}),$ $\dots ,$ $(x_q,y_q)$が、図でも折れ線の1つの線分上に等間隔に並ぶ。(図には折れ線を3つしか表示できないが、実際には$x$軸/$y$軸に限りなく近づきながら折れ線が多数続くこともある。)
原点$O$から、プロットした各点までの位置ベクトルを考える。これらの中から好きなベクトルを好きな個数選んで加算していき、原点と点$(X,Y)$で囲まれる長方形からはみ出さないという条件のもとで、最大何個加算できるか、という問題になる。
何となく、$(X,Y)$方向の両脇の2つのベクトル$U,V$だけを使えば良さそうに見える。そのつもりで考えると、実際にそうであることを証明できる。
「両脇」のみで良いことの証明
原点と$(X,Y)$を通る直線より左上の領域を$G$、右下の領域を$H$とする。加算したベクトルの集合$S$が個数最大の解であるとする。領域$G$内で$U$以外のベクトルが$S$に含まれていたら、$S$に含まれ領域$H$にあるベクトルを1つ選び、両ベクトルを近づけるように1つずつ動かしても、やはり条件を満たしたままであり(ベクトルの合計の$x$座標も$y$座標も同じか小さくなるため)、最適解である。これを繰り返せば、領域$G$内では$U$しか含まない最適解を構成できる。もし繰り返している途中で、領域$H$内のベクトルが$S$に1つもなくなったら、それはつまり$S$が全て領域$G$内のベクトルであるということであり、全ベクトルを$U$とするのが最適解(の1つ)である。よって、いずれにせよ領域$G$内では$U$のみ使うとしてよい。同様にして、領域$H$内では$V$のみ使うとしてよい。
個数の計算
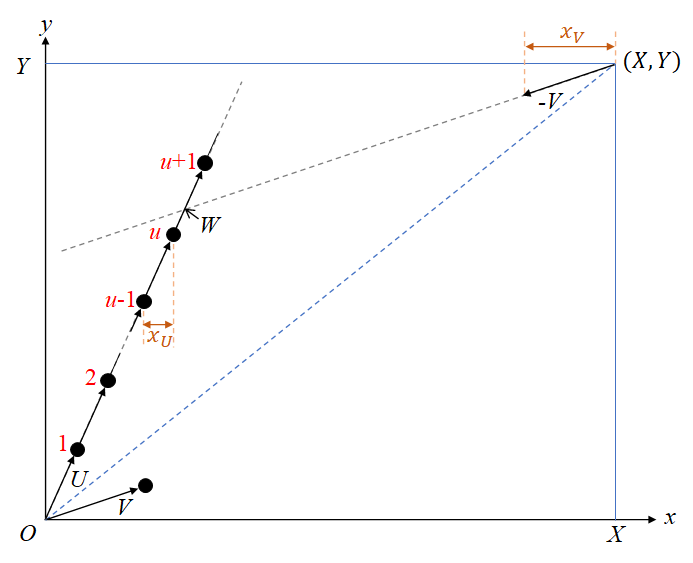
最後に、ベクトル$U$と$V$を何個ずつ足すのが最適か求める。原点からベクトル$U$を加える個数分だけ伸ばし、$(X,Y)$からベクトル$V$を加える個数分だけマイナス方向に伸ばしたときに、ベクトル$U$側が「左下」、ベクトル$V$側が「右上」になっていればよい。その条件を満たした上で、$U$と$V$の個数の和を最大にしたい。
$U=(x_U,y_U),$ $V=(x_V,y_V)$とする。下図のように、原点からベクトル$U$方向に伸びる直線と、$(X,Y)$からベクトル$-V$方向に伸びる直線の交点を$W$とする。すると、最適解の1つは、$W$をまたぐ位置の両脇、すなわち、ベクトル$U$の個数が下図における$u$個か$u+1$個のいずれかになる。なぜなら、例えばベクトル$U$が$u-1$個のときを考えてみると、$u$個のときに比べ$x$方向に$x_U$後退する。しかし、$x_V$は$x_U$より大きいので、この後退により$U$と$V$の個数の和が増加することはあり得ない。同様に、$u+2$個のときは、$y_V<y_U$であることを用いて増加があり得ないことが示せる。よって、ベクトル$U$が$u$個のときと$u+1$個のときの2通りを試すことで答が求まる。$u$の値は、二分探索をする、交点$W$を計算する、などの方法で求めることができる。
感想
問題文はシンプルで取っつきやすいのに、何段階もの考察が必要で、奥の深いすごい問題だと思いました。相当な日数を費やしましたが、解けただけで大満足です。