始めに
今回は、ビットコイン価格の予測を行います。
予測と一口に言っても、色々とやり方はあると思いますが、ここでは、
直近30日間の終値データを使い、次の日の終値を予測するRNNモデルを作成します。
CNTKのシーケンス処理
CNTKでは、RNNなどのシーケンス処理について、特定のコンセプトに基づいて実装を行っています。
ここでは概要のみを紹介しようと思いますので、詳しいことはリンク先を参照して下さい。
静的軸・動的軸・シーケンス軸
CNTKでは、テンソルの次元を軸として扱い、その軸を性質毎に種類分けしています。
- 静的軸 ... ネットワークの学習終了時まで、要素数が変化しない軸。
- 動的軸 ... バッチ軸とも呼ばれる。ミニバッチの長さに対応する軸。
- シーケンス軸 ... バッチ軸とは異なる動的軸。シーケンスの長さに対応する軸。
この中でもシーケンス軸は、名前の通りシーケンス情報に関する軸であり、
この軸を有する入力データ/出力データのプレースホルダと、それに関するパラメータを持つ処理は、
シーケンス処理専用のパッケージ/モジュールで実装しなければなりません。
CNTKテンソルの軸についての具体例
上記で紹介した、3つの軸の理解を深めるために、いくつか具体例を紹介します。
尚、どの例もミニバッチ数を10としています。
-
1次元の終値データ30点を1シーケンスとし、ネットワークに入力する場合
この時の入力データの次元は、$10×30×1$ = (batch, seq, data_vec)となり、
各軸は(動的軸、シーケンス軸、静的軸)と対応します。 -
100次元の文字ベクトル12個から成る文章を1シーケンスとし、ネットワークに入力する場合
この時の入力データの次元は、$10×12×100$ = (batch, seq, word_vec)となり、
各軸は(動的軸、シーケンス軸、静的軸)と対応します。 -
横:640pix、縦:480pix、チャネル:3、枚数:5の動画を1シーケンスとし、ネットワークに入力する場合
この時の入力データの次元は、$10×5×3×640×480$ = (batch, seq, channel, width, height)となり、
各軸は(動的軸、シーケンス軸、静的軸、静的軸、静的軸)と対応します。
シーケンス用パッケージ/モジュール
CNTKには、以下2点のシーケンス処理専用のパッケージ/モジュールが実装されており、
RNNなどのシーケンス情報を扱うモデルを作成する場合に必須となります。
モジュールのインポート
import cntk as C
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
データの準備
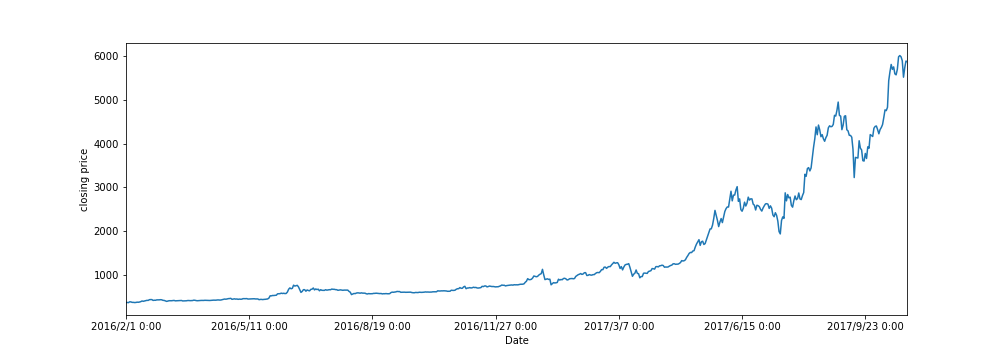
ビットコインの時系列データは、coindeskからダウンロードしました。
今回の計算では、2016/02/01 - 2017/10/27 までの各日の終値データを使用します。
(データ点は全部で635点)
# 終値データ
close_data = pd.read_csv('coindesk-bpi-USD-close_data-2016-02-01_2017-10-27.csv')
データ加工
始めに、時系列データの学習期間と検証期間について、設定を行います。
今回は、取得したデータ期間635日中、後半90日分を検証期間、それ以外の期間を学習期間とみなします。
# 検証日数
n_valid = 90
# 学習日数
n_train = len(close_data) - n_valid
次に、時系列データの標準化を行います。
ここでは、学習データ分布を$N(0,1)$の標準正規分布に変換するようなパラメータを推定し、
推定したパラメータを用いて時系列データ全体を変換しています。
# 終値データの標準化
clf = StandardScaler()
clf.fit(close_data[:n_train])
close_data_std = clf.transform(close_data)
冒頭でも述べましたが、今回の時系列予測では、『直近30日間の終値データを使い、次の日の終値を予測』する
ため、RNNの入力データは直近30日分のシーケンスデータ、出力データは翌日のデータになります。
上記の形になるよう、特徴量データ(入力データ)と教師データ(出力データの評価に使用)を作成します。
feature_list = [] # 特徴量データを保管するリスト
target_list = [] # 教師データを保管するリスト
length_of_sequences = len(close_data) # 全期間の長さ
maxlen = 30 # 入力データの最大シーケンス長
for i in range(0, length_of_sequences - maxlen):
# 1日ずつずらしながら、特徴量データと教師データを取得
feature_list.append(close_data_std[i:i+maxlen])
target_list.append(close_data_std[i+maxlen])
x = np.array(feature_list).reshape(len(feature_list), maxlen, 1).astype(np.float32) # x.shape=(batch, seq, data_vec)
y = np.array(target_list).reshape(len(target_list), 1).astype(np.float32) # y.shape=(batch, data_vec)
# 学習データと検証データに分割
x_train, x_test, y_train, y_test = x[:n_train], x[n_train:], y[:n_train], y[n_train:]
モデルの設定
RNN関数の定義
ここでは、1つの中間層(LSTM層)から成るRNNを定義します。
CNTKでは、以下のようにRNN関数を記述します。
n_in = len(x[0][0]) # =1
n_hidden = 50
n_out = len(y[0]) # =1
def lstm_sequence_model(features):
m = C.layers.Recurrence(C.layers.LSTM(n_hidden))(features)
m = C.sequence.last(m)
output = C.layers.Dense(n_out)(m)
return output
- n_in/n_outは、入力データ/出力データの静的軸のshapeになります。
各終値データは1次元ベクトルになりますので、n_in/n_outは共に1となります。 - n_hiddenは、LSTM層の出力次元数を表します。
-
C.layers.Recurrence()は、RNNモデルを実装するのに必須となる関数です。
この関数は、入力データのシーケンス長分だけ、引数で引き渡したLSTM関数を実行し、
全てのLSTM層の出力値を返します1。 -
C.sequence.last()は、引数に与えられたシーケンスの最後の要素を返します。
ここではRecurrence()の返り値を引数に与えているため、時間軸上で最後となるLSTM層の出力値を返すこと
になります2。
m = C.layers.Recurrence(C.layers.LSTM(n_hidden))(features)
m = C.sequence.last(m)
を
m = C.layers.Fold(C.layers.LSTM(n_hidden))(features)
と書き換えればよい。
モデルオブジェクトの作成
RNN関数を定義した後は、モデルオブジェクトを作成します。
features = C.sequence.input_variable(n_in) # シーケンス処理用の入力プレースホルダを作成
model_output = lstm_sequence_model(features)
targets = C.input_variable(n_out, dynamic_axes=model_output.dynamic_axes)
- 特徴量データはシーケンスデータであるため、シーケンス用のプレースホルダを作成することになります。
C.sequence.input_variable()の引数shapeには、シーケンスデータの静的軸のshapeを入力します。 - 教師データはシーケンスデータでないため、通常のプレースホルダを作成することになります。
C.input_variableには、教師データの静的軸のshapeを入力します。
学習設定
最適化手法の設定
今回は、Adamを採用します。
batch_size = 10
lr_schedule = C.learners.learning_rate_schedule(0.002, unit=C.UnitType.minibatch)
momentum_time_constant = C.momentum_as_time_constant_schedule(batch_size / -np.log(0.9))
optimizer = C.adam(model_output.parameters,
lr = lr_schedule,
momentum = momentum_time_constant)
損失関数の設定
訓練に必要となる損失関数を設定します。
今回作成するモデルは回帰問題に当たるので、損失関数に二乗誤差を採用します。
loss = C.losses.squared_error(model_output, targets)
trainer = C.Trainer(model_output, loss, optimizer)
学習実行
エポック数200、バッチサイズ10で、計算を行います。
# 学習を実行する
n_epoch = 200
batch_size = 10
n_step = 1
loss_list = []
for epoch in range(n_epoch):
for i in range(0, len(y_train), batch_size):
# バッチ毎に訓練データを抽出
x_batch = x_train[i:i+batch_size]
y_batch = y_train[i:i+batch_size]
# 訓練データを用いて、モデルパラメータを更新
trainer.train_minibatch({features: x_batch, targets: y_batch})
# 100ステップ毎に精度を出力
if n_step % 10 == 0:
# 訓練データに対して損失を算出
train_loss = loss.eval({features: x_train, targets: y_train}).mean(axis=0)
# 検証データに対して損失を算出
test_loss = loss.eval({features: x_test, targets: y_test}).mean(axis=0)
loss_list.append((train_loss, test_loss))
print("Epoch: %s, Step:%s, Train Loss: %.4f, Test Loss: %.4f,"
% (epoch+1, n_step, train_loss, test_loss))
n_step += 1
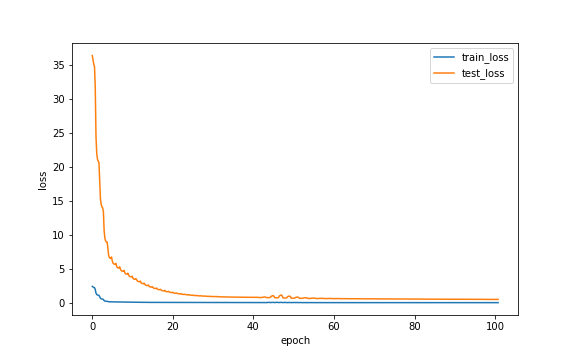
以下の図は、損失の推移を表しています。
学習データに対する損失と検証データに対する損失に大きな差異がありますが、
両者とも減少傾向にあることから、一先ず学習が進んでいることは確認できます。
予測
作成したRNNモデルを使って、検証データに対する予測値を算出してみます。
y_test_pred = model_output.eval({features: x_test})
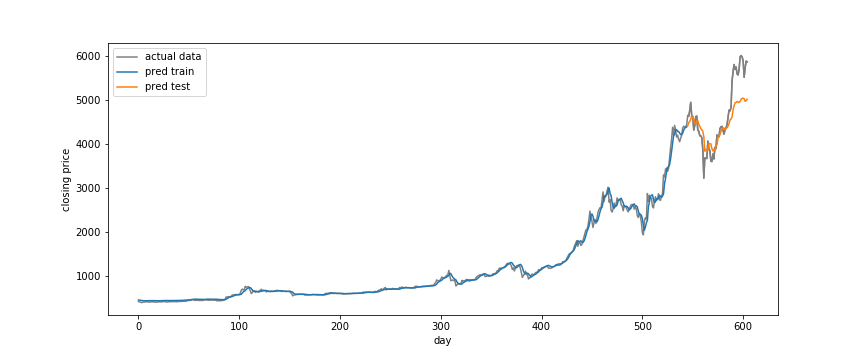
以下の図は、実際の終値データと予測値をプロットしたものです。
学習期間の予測値は実際の終値とほぼ一致しているのに対し、
検証期間の予測値は実際の終値とやや乖離しているのが確認できます。
以上