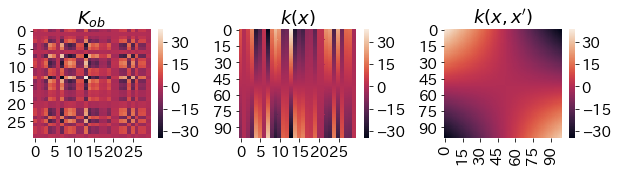scikit-learnでガウス過程回帰

from IPython.display import HTML

HTML('''
<script>  
code_show=true; 
function code_toggle() {
  if (code_show){
    $(\'div.input\').hide();
  } else {
    $(\'div.input\').show();
  }
  code_show = !code_show
}  
$( document ).ready(code_toggle);
</script>
<form action="javascript:code_toggle()">
    <input type="submit" value="Toggle code">
</form>
''')

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn.gaussian_process as gp
%matplotlib inline
plt.rcParams['font.size']=15

def plt_legend_out(frameon=True):
    plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, frameon=frameon)

線形回帰

カーネル関数

$k(x,x')=xx'+\sigma^2I\ \ \ [x=x']$

# カーネル関数 k(x,x') を定義
def GPk(xv,zv,sd=1):
    return(np.outer(xv,zv) + sd**2 * np.equal.outer(xv,zv))

n, sd = 30, 0.5;  # 設定
theta = 1           # 回帰係数
# データ生成
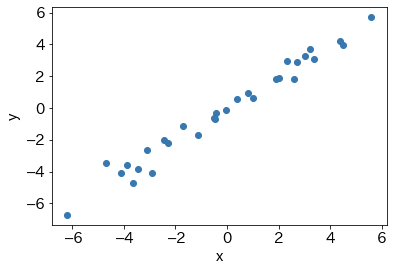
X = np.random.normal(scale=3,size=n)
Yob = np.dot(X,theta) + np.random.normal(scale=sd,size=n)
newx = np.linspace(X.min(),X.max(),100) # 予測点 

plt.scatter(X,Yob)
plt.xlabel('x')
plt.ylabel('y')
plt.show()

y\sim N(k(x)^TK^{-1}_{ob}y_{ob},k(x,x)-k(x)^TK^{-1}_{ob}k(x))

# カーネル関数の計算
Kob  = GPk(X,X,sd=sd)
kx   = GPk(newx,X,sd=sd)
knewx = GPk(newx,newx,sd=sd)

plt.figure(figsize=(10,2))
plt.subplots_adjust(wspace=0.4)

plt.subplot(131)
sns.heatmap(Kob)
plt.title('$K_{ob}$')

plt.subplot(132)
sns.heatmap(kx)
plt.title('$k(x)$')

plt.subplot(133)
sns.heatmap(knewx)
plt.title('$k(x,x\')$')

plt.show()

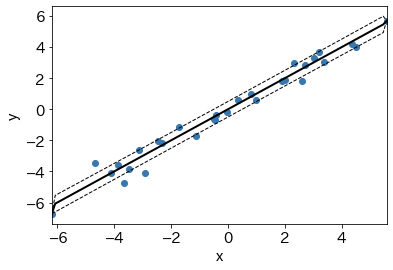
# ガウス過程による回帰関数の予測
GPf = np.dot(kx, np.linalg.solve(Kob,Yob))
GPv = np.maximum(np.diag(knewx- np.dot(kx, np.linalg.solve(Kob,kx.T))),0)

# プロット
plt.xlim(X.min(),X.max())
plt.scatter(X,Yob)                   # データ点
plt.plot(newx, GPf, 'k-', lw=2)  # 推定した回帰関数
# 信頼区間
plt.plot(newx, GPf+np.sqrt(GPv), 'k--', lw=1)
plt.plot(newx, GPf-np.sqrt(GPv), 'k--', lw=1)
plt.xlabel('x')
plt.ylabel('y')
plt.show()

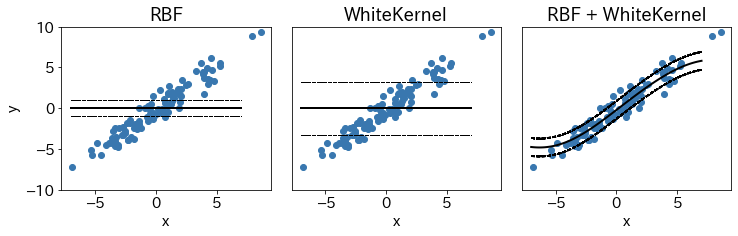
非線形回帰

• ガウスカーネル：RBF
• ホワイトカーネル：$I\ \ \ [x=x']$

# トレーニングデータの生成
n, sd = 100, 1    # 設定
theta = 1            #  回帰係数
X = np.random.normal(scale=3, size=n).reshape(n,-1)
Yob = np.dot(X,theta) + np.random.normal(scale=sd,size=n).reshape(n,-1)

# プロット
plt.figure(figsize=(12,3))
plt.subplots_adjust(wspace=0.1)

plt.subplot(131)
kk = gp.kernels.RBF()
#kk = gp.kernels.WhiteKernel()
#kk = gp.kernels.RBF() + gp.kernels.WhiteKernel()
gpm = gp.GaussianProcessRegressor(kernel=kk)
gpm.fit(X, Yob)                                # データへのフィッティング
newx = np.linspace(-7,7,100).reshape(100,-1)   # 予測点
GPf, GPv = gpm.predict(newx, return_cov=True)  # 予測値と分散共分散行列
GPsd = np.sqrt(np.diag(GPv))                   # 予測値の標準偏差
plt.ylim(-10,10)
plt.scatter(X,Yob)
plt.plot(newx, GPf,'k-', lw=2)
plt.plot(newx, GPf+GPsd,'k--', lw=1)
plt.plot(newx, GPf-GPsd,'k--', lw=1)
plt.xlabel('x')
plt.ylabel('y')
plt.title('RBF')

plt.subplot(132)
#kk = gp.kernels.RBF()
kk = gp.kernels.WhiteKernel()
#kk = gp.kernels.RBF() + gp.kernels.WhiteKernel()
gpm = gp.GaussianProcessRegressor(kernel=kk)
gpm.fit(X, Yob)                                # データへのフィッティング
newx = np.linspace(-7,7,100).reshape(100,-1)   # 予測点
GPf, GPv = gpm.predict(newx, return_cov=True)  # 予測値と分散共分散行列
GPsd = np.sqrt(np.diag(GPv))                   # 予測値の標準偏差
plt.ylim(-10,10)
plt.scatter(X,Yob)
plt.plot(newx, GPf,'k-', lw=2)
plt.plot(newx, GPf+GPsd,'k--', lw=1)
plt.plot(newx, GPf-GPsd,'k--', lw=1)
plt.xlabel('x')
plt.tick_params(left=False,labelleft=False)
plt.title('WhiteKernel')

plt.subplot(133)
#kk = gp.kernels.RBF()
#kk = gp.kernels.WhiteKernel()
kk = gp.kernels.RBF() + gp.kernels.WhiteKernel()
gpm = gp.GaussianProcessRegressor(kernel=kk)
gpm.fit(X, Yob)                                # データへのフィッティング
newx = np.linspace(-7,7,100).reshape(100,-1)   # 予測点
GPf, GPv = gpm.predict(newx, return_cov=True)  # 予測値と分散共分散行列
GPsd = np.sqrt(np.diag(GPv))                   # 予測値の標準偏差
plt.ylim(-10,10)
plt.scatter(X,Yob)
plt.plot(newx, GPf,'k-', lw=2)
plt.plot(newx, GPf+GPsd,'k--', lw=1)
plt.plot(newx, GPf-GPsd,'k--', lw=1)
plt.xlabel('x')
plt.tick_params(left=False,labelleft=False)
plt.title('RBF + WhiteKernel')

plt.show()

判別分析

まずはパラメトリックモデルの仮定。$\tau(z)$はシグモイド関数や標準正規分布の分布関数

$p(y|x;w)=\tau (y\color{red}{x^Tw})$

2値分類問題の場合、$\tau(z)$の性質より$\color{red}{x^Tw} \geq 0$なら$y=1$、$\color{red}{x^Tw} <0$なら$y=-1$

点$x$でのラベル$y$の予測分布

$p(y|x;D)=\int \tau(y\color{red}{x^Tw})p(w|D)dw$

ノンパラ

判別分析では、ラプラス近似で事後分布を求める。事後分布の対数を最大化する点を$f=\tilde{f}$とし、その周りでテーラー展開する。

$p(f|D)\propto \color{red}{p(y|f)}p(f)=\color{red}{\sum_{i=1}^n\tau(y_if(x_i))}p(f)$

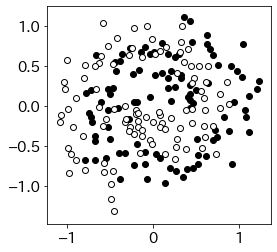
from common import mlbench as ml                      # code_mlbench.spirals を使う
X, y = ml.spirals(200,cycles=1.2,sd=0.16)           # データ生成

plt.figure(figsize=(4,4))
plt.scatter(X[y==0,0],X[y==0,1],color='k')
plt.scatter(X[y==1,0],X[y==1,1],color='w',edgecolors='k')
plt.show()

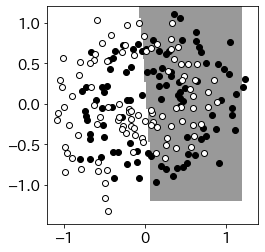
kk = gp.kernels.RBF()+gp.kernels.WhiteKernel()  # カーネル設定
gpm = gp.GaussianProcessClassifier(kernel=kk)
gpm.fit(X,y)                              # データ・フィッティング
m = 100; newx = np.linspace(-1.2,1.2,m)   # 予測点生成
newdat = np.array([(y, x) for x in newx for y in newx])
GPpred = gpm.predict(newdat)              # 予測ラベル
# プロット
ext=(-1.2,1.2,-1.2,1.2)
plt.figure(figsize=(4,4))
plt.imshow(GPpred.reshape(m,-1)[::-1],cmap='gray',extent=ext, alpha=0.4)
plt.scatter(X[y==0,0],X[y==0,1],color='k')
plt.scatter(X[y==1,0],X[y==1,1],color='w',edgecolors='k')
plt.show()

ベイズ最適化

ベイズ最適化の流れ（最小化問題の場合）

1. 繰り返し点数$T$、カーネル関数、獲得関数$a(x)$、関数評価の初期点$x_1$を定める
2. 以下を$T$回繰り返す
   1. 入力$x_t$に対する出力$y_t$を得る
   2. これまでの最適値$\hat{f}=\min_{t'=1\cdots t}{y_{t'}}$ と対応する$x_{opt}\in {x_1,\cdots x_t}$を求める
   3. 獲得関数$a(x)$を更新する
   4. $a(x)$の最適値を達成する解を$x_{t+1}$とする
3. 最適値$\hat{f}$を達成する$x_{opt}$を得る

期待改善量（EI, Expected Improvement）$a_{EI}(x)$

$a_{EI}(x)$を最大にする$x$を求め、その点における$f(x)$の値を観測する。

$$
\begin{eqnarray}
a_{EI}(x) &=& \mathbb{E}_{Z\sim N(\mu(x),v(x))}\left [\max{{0,\hat{f}-f(Z)}}\right ]\
&=& (\hat{f}-\mu(x))\color{red}{\Phi(\hat{f};\mu(x),v(x))}+v(x)\color{blue}{\phi(\hat{f};\mu(x),v(x))}
\end{eqnarray}
$$

$\color{red}{\Phi(f;\mu(x),v(x))}$は正規分布の分布関数の$f$における値、$\color{blue}{\phi(f;\mu(x),v(x))}$は対応する確率密度関数の$f$における値

上側信頼限界（UCB, upper confidence bound）※本来は最大化問題に対して使用されるため「上側」と呼ばれるが、今回は最小化問題について考えているので「下側」と考えて良い。信頼区間の下限が最も小さくなる点を選ぶ。$v$は分散、$\kappa$は重み（自分で決める）。

$a_{UCB}(x)=\mu(x)-\kappa \sqrt{v(x)}$

from sklearn.svm import SVC
from sklearn.model_selection import cross_validate
from skopt import gp_minimize
from scipy.spatial import distance           # distanceの計算

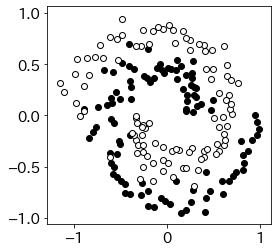
X,y = ml.spirals(200,cycles=1,sd=0.1,label=[0,1]) # データ生成

plt.figure(figsize=(4,4))
plt.scatter(X[y==0,0],X[y==0,1],color='k')
plt.scatter(X[y==1,0],X[y==1,1],color='w',edgecolors='k')
plt.show()

目的関数を定義。CV=5としたときのスコア。logCとlogsigはそれぞれ正則化パラメータ$C$の対数とカーネル幅の対数

# 目的関数を定義
def svmcv(par):
    logC, logsig = par
    sv = SVC(kernel="rbf", gamma=10**logsig, C=10**logC)
    cv = cross_validate(sv,X,y,scoring='accuracy',cv=5)
    return(1-np.mean(cv['test_score']))

# カーネル幅の範囲をデータから決める
from scipy.spatial import distance               # distanceの計算
cg = np.log10(1/np.percentile(distance.pdist(X),[1,99])**2)
space = [(-5.,5.), (cg[1],cg[0])]

%%time
x0 = [0., np.mean(cg)]
op = gp_minimize(svmcv,space,x0=x0,acq_func="EI",n_calls=100,verbose=False)
#op = gp_minimize(svmcv,space,x0=x0,acq_func="EI",n_calls=100,verbose=True)

CPU times: user 1min 41s, sys: 2min 6s, total: 3min 47s
Wall time: 37.4 s

optC,optsig = 10**np.array(op.x)
print('optC  ',optC)
print('optsig',optsig)

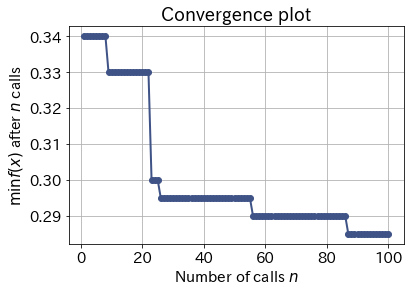
from skopt.plots import plot_convergence
plot_convergence(op)
plt.show()

optC   31405.928164443125
optsig 0.2932912067899352

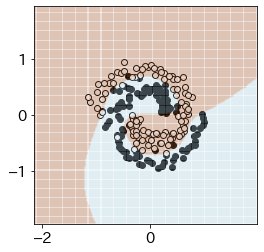
sv = SVC(kernel="rbf", gamma=optsig, C=optC)
sv.fit(X, y)

h = .02  # step size in the mesh

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = sv.predict(np.c_[xx.ravel(), yy.ravel()])

Z = Z.reshape(xx.shape)

plt.figure(figsize=(4,4))
plt.scatter(X[y==0,0],X[y==0,1],color='k')
plt.scatter(X[y==1,0],X[y==1,1],color='w',edgecolors='k')
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.1)
plt.show()