データ分析初心者のＳＥがデータサイエンス部隊と一緒に学ぶ vol.1

はじめに

こんにちは！(株) 日立製作所 Lumada Data Science Lab. の中川です。

Lumada Data Science Lab. では、お客様へのご提案品質の向上を目的として、社内の SE を積極的に実習生として受け入れて、データサイエンティストを育成しています。実習では定期的にデータ分析のお題に挑戦して、データ分析業務に従事する研究所のメンバと、お題で生じた疑問点をディスカッションしています。この記事では、そのデータ分析やディスカッションの内容をご紹介したいと思います。

データ分析を始めたばかりの方がつまづきやすい問題の解決策を共有したり、データ分析を既に業務としている方にも有効なテクニックを共有したりする事で、データ分析とは何かをみんなで考える機会となれば良いなと考えています。

実習生のプロフィール

• 松下さん (入社9年目の男性)
  • 公共システム事業部で社会保障関連の SE 業務に従事
  • Java や C 言語での開発経験はあるがデータ分析は未経験
  • 海外旅行やお酒が大好きなアクティブ系中堅 SE

演習の内容

ここでは演習について、松下さんが具体的にまとめた内容をご紹介します。

お題

• Python と scikit-learn を用いて重回帰分析をします。 (開発環境は Python を使ったデータ分析で便利な Jupyter Notebook)
• scikit-learn には、データ分析・機械学習をすぐに試せるように、いくつかの 付属データセットがあります。
• 今回は付属データセットのうち、ボストン住宅価格問題 (Boston house prices dataset) に取り組みます。
• データ分析は CRISP-DM のプロセスを参考にして行います。

0. CRISP-DM

データ分析を進める上で有効な考え方がCRISP-DM (CRoss-Industry Standard Process for Data Mining) です。以下のプロセスに分かれており、お客様のビジネス課題の理解から、実際のモデリング、その評価とビジネスへの展開 (業務改善) まで、PDCAサイクルを回しながらデータ分析を行うデータマイニングの方法論及びプロセスモデルです。

1. ビジネスの理解
2. データの理解
3. データの準備
4. モデリング
5. 評価
6. 展開

今回のお題についても、この順番に沿って取り組みました。

1. ビジネスの理解

ビジネス上の課題を明確化し、データ分析を行う上での目標を設定します。今回はすでに解くべき課題が明確になっているので以下とします。

目標：ボストン住宅価格の数値予測モデルの作成と評価

2. データの理解

データ分析の対象となるデータを確認し、そのまま使用可能か、データの加工が必要か方針を決定します。具体的には、欠損や外れ値が多くてそのままデータ分析に使えないデータがないかを確認し、使えないデータがあれば削除や補完などのデータ加工の方針を決めます。

データの読み込み

使用するライブラリをインポートし、データ分析の対象データを読み込みます。

# ライブラリのインポート
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
%matplotlib inline

# データセットの読み込み
from sklearn import datasets
boston_data = datasets.load_boston()

# 説明変数の格納
boston = pd.DataFrame(boston_data.data, columns=boston_data.feature_names)

# 目的変数 (住宅価格) の格納
boston_medv = pd.DataFrame(boston_data.target)

# データの確認
boston.info()

今回のデータ分析の対象となるBoston house prices datasetの変数は以下の通りです。

カラム名	内容
CRIM	町ごとの1人当たりの犯罪率
ZN	25,000平方フィートを超える区画に分けられた住宅地の割合
INDUS	町当たりの非小売業の面積の割合
CHAS	チャールズリバーのダミー変数 (=河川の境界にある場合は1、それ以外の場合は0)
NOX	一酸化窒素濃度 (1000万分の1)
RM	住居ごとの部屋の平均数
AGE	1940年より前に建てられた住居の割合
DIS	5つのボストンの雇用センターまでの距離 (重み付き)
RAD	放射状高速道路へのアクセシビリティの指標
TAX	10,000ドルあたりの固定資産税率
PTRATIO	町ごとの生徒-教師の比率
B	「1000(Bk - 0.63)^2」で算出した居住割合の指標 ※Bkは町ごとのアフリカ系アメリカ人の割合
LSTAT	人口当たりの低所得者の割合
MEDV	1000ドル単位での住宅価格の中央値 ※目的変数

欠損値の確認

Boston house prices dataset に欠損値がないか確認します。

# 欠損値の確認
boston.isnull().sum()

出力結果

# 欠損値の数
CRIM       0
ZN         0
INDUS      0
CHAS       0
NOX        0
RM         0
AGE        0
DIS        0
RAD        0
TAX        0
PTRATIO    0
B          0
LSTAT      0
dtype: int64

今回のデータには欠損値がないことが確認できました。

外れ値・異常値の確認

外れ値・異常値についてはそもそも何を外れ値・異常値として扱うかを考える必要があります。このためにはデータ分析の対象となるビジネス・事象の背景や、測定方法等のデータの背景を理解する必要があります。背景を理解した上で、例えば以下のような観点で外れ値・異常値を判断します。

• 変数の性質上、明らかにありえない値ではないか (例：年齢がマイナスや文字列などの値の場合)
• ビジネスや事象の性質上、ありえない値ではないか (例：ローンの申込可能年齢に制限があるが、制限を満たさない値の場合)
• 変数の確率分布が想定できる場合、大きく異なる分布となっていないか (例：正規分布の想定に対して、両極端な値が頻出している場合)

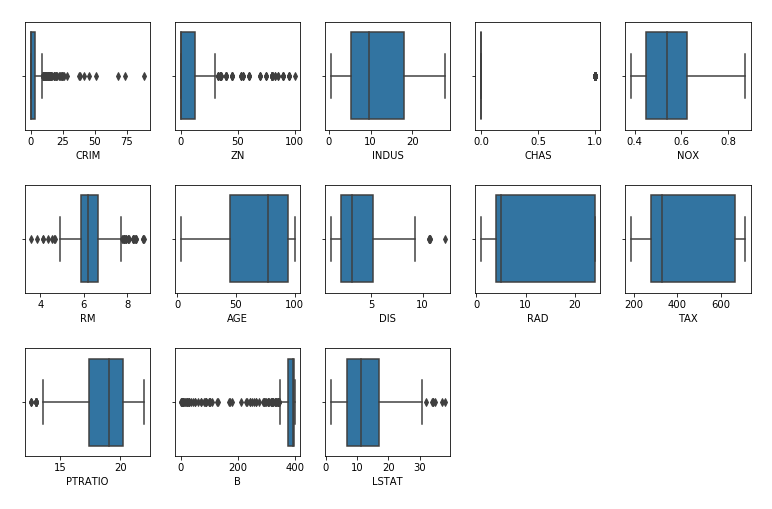
まずは値のばらつきを箱ひげ図を用いて確認します。

# 箱ひげ図で外れ値を確認 (タイル状に可視化)
fig, axs = plt.subplots(ncols=5, nrows=3, figsize=(13, 8))
for i, col in enumerate(boston.columns):
    sns.boxplot(boston[col], ax=axs[i//5, i%5])

# グラフ間隔の調整   
fig.subplots_adjust(wspace=0.2, hspace=0.5)

# 余白の削除
fig.delaxes(axs[2, 4])
fig.delaxes(axs[2, 3])

出力結果

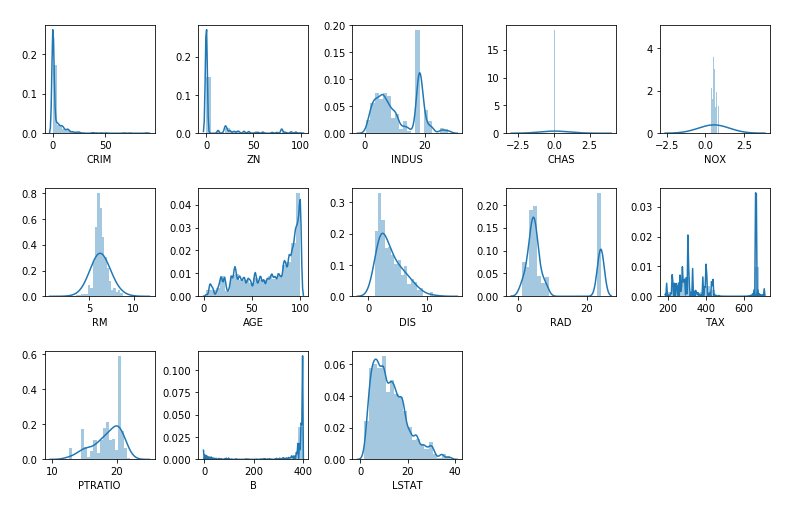
箱ひげ図を確認すると CRIM, ZN, CHAS, RM, DIS, PTRATIO, B, LSTAT の値のばらつきが多く、外れ値を含む可能性がありそうです。さらに、ヒストグラムを用いて具体的な変数の値と分布を確認します。

# ヒストグラムで分布を確認　(タイル状に可視化)
fig, axs = plt.subplots(ncols=5, nrows=3, figsize=(13, 8))
for i, col in enumerate(boston.columns):
    sns.distplot(boston[col], bins=20, kde_kws={'bw':1}, ax=axs[i//5, i%5])

#グラフ間隔の調整
fig.subplots_adjust(wspace=0.2, hspace=0.5)

#余白の削除
fig.delaxes(axs[2, 4])
fig.delaxes(axs[2, 3])

出力結果

変数の性質を想像しながらヒストグラムを確認したところ、取り得る値であると見受けられるため、ここでは外れ値・異常値として扱わないこととします。"CHAS" は箱ひげ図・ヒストグラムとも特殊な形となりますが、これは川沿いかどうかを 0, 1 でフラグ化したダミー変数であるためです。

3. データの準備

「データの理解」で決定した方針に従い、次のモデリングに投入可能な状態にデータを加工します。例えば、以下のような処理を行います。

• 欠損値・外れ値・異常値を平均値や最頻値で補完または除外
• 数値データを意味のある単位で区切り、カテゴリデータに変換
• ラベルデータを数値として取り扱うためにフラグ化

「データの理解」で確認した通り、欠損値・外れ値・異常値はないものとして次フェーズへ進みます。

4. モデリング

データ分析の条件に適した手法でモデリングを行います。モデルに投入する変数を選択し、データをモデルの学習用とテスト用に分けてデータ分析に用います。今回はモデル化のアルゴリズムとして、線形回帰分析 (重回帰) を選択します。ちなみに、scikit-learnではどのアルゴリズム・モデリング手法を使用すると良いかの選択指標がcheat sheet にまとめられています。

変数の選択

モデルに投入する変数を選択します。実際に使用する変数の数を減らしつつ、有効な組み合わせを探索するプロセスです。使用する変数を減らすことには、下記のようなメリットがあります。

• 計算コストを下げて、処理時間を短縮する
• 過学習 (オーバーフィッティング) を避けて汎化性 (未知のデータへの予測性能) を向上させる

変数の選択方法には以下のような手法があります。

• Filter Method: 評価指標に基づいて変数をランク付けし、上位の変数を選択する手法
• Wrapper Method: 複数の変数の組み合わせで実際にモデリングを行い、 最も結果の良い変数の組み合わせを選択する手法
• Embedded Method: 機械学習アルゴリズムの中で同時に変数も選択する手法

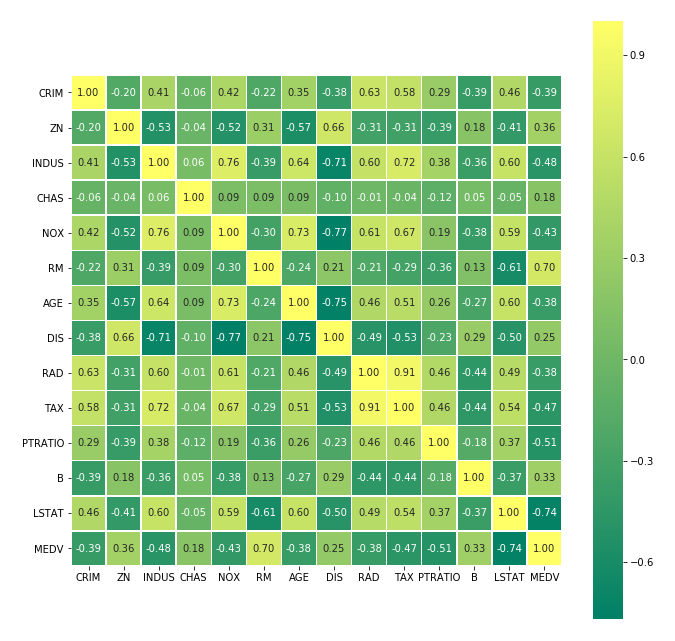
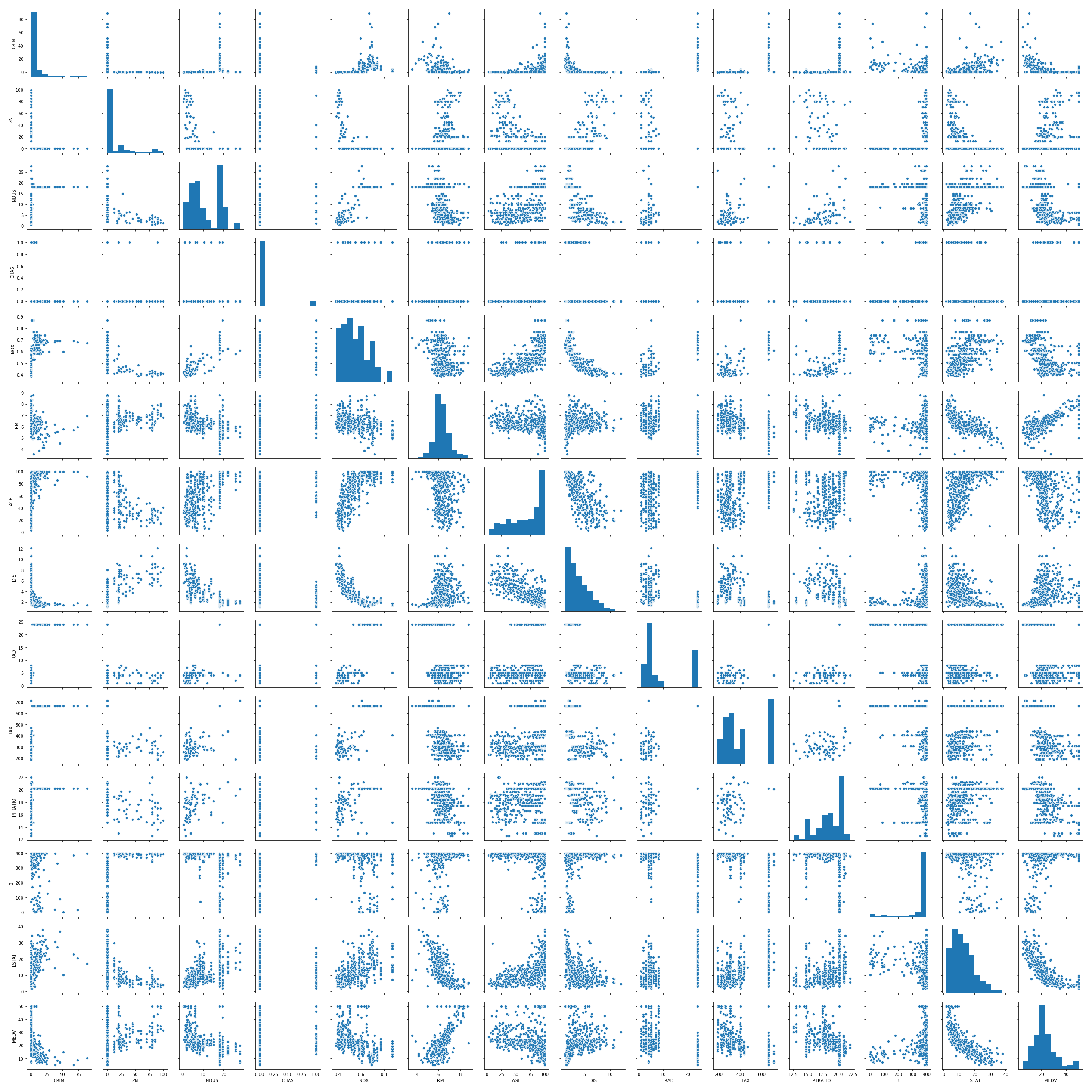
今回はFilter Method の方法論に則り、変数間の相関の強さを確認する方法を例として記載します。pairplotを用いると各変数のヒストグラムと、全ての2変数の組合せの相関を可視化してくれるので便利です。

# seaborn の heatmap を用いて量的変数の相関を数値化
boston["MEDV"] = boston_medv
plt.figure(figsize=(11, 11))
sns.heatmap(boston.corr(), cmap="summer", annot=True, fmt='.2f', square=True, linewidths=.5)
plt.ylim(0, boston.corr().shape[0])
plt.show()
# seabornのpairplotを用いて量的変数の相関をグラフで可視化
sns.pairplot(boston)
plt.show()

出力結果

heatmapを確認するとRADとTAXの間に強い正の相関があるため、ここでは2変数のうちMEDVとの負の相関がより強いTAXを選択します。

学習用・テスト用データの分割

データのうち一部をモデル学習に用い、残りを作成したモデルの予測能力の検証に用いる方法が一般的です。今回は学習用とテスト用で 50％ ずつのデータを用いることとします。

# 説明変数、目的変数を Xm, Ym にそれぞれ格納
Xm = boston.drop(['MEDV', 'RAD'], axis=1)
Ym = boston.MEDV

# trainデータとtestデータの分割を行うライブラリを import
from sklearn.model_selection import train_test_split

# X_train, X_test に振り分けられるデータはランダムに決まる
# test_size=0.5で 50% をtestに振り分け
X_train, X_test = train_test_split(Xm, test_size=0.5, random_state=1234) 
Y_train, Y_test = train_test_split(Ym, test_size=0.5, random_state=1234) 

モデルフィッティング

実際にデータを与えて線形回帰モデル (重回帰モデル) にフィッティングします。

# sklearnの線形回帰モデルをimportし、trainデータでフィッティング
from sklearn import linear_model
model_lr = linear_model.LinearRegression()
model_lr.fit(X_train, Y_train)

# 生成されたモデルを用いて、testデータの説明変数に対する予測値を取得
predict_lr = model_lr.predict(X_test)

# 回帰係数
print(model_lr.coef_)
# 切片
print(model_lr.intercept_)

出力結果

# 回帰係数
[-2.79020004e-02  5.37476665e-02 -1.78835462e-01  3.58752530e+00
 -2.01893649e+01  2.15895260e+00  1.95781711e-02 -1.66948371e+00
  6.47894480e-03 -9.66999954e-01  3.62212576e-03 -6.65471265e-01]
# 切片
48.68643686655955

　　

5. 評価

作成したモデルの精度・性能等を評価し、目標を達成可能か判断します。また、評価結果をもとに必要に応じてモデルのチューニングを行います。

モデルの評価

モデルの精度評価では、以下の指標を用いて作成したモデルの予測値と正解値の誤差や相関の強さを評価します。

• MAE (Mean Absolute Error): 誤差の絶対値の平均
• MSE (Mean Squared Error): 誤差の二乗の平均
• RMSE (Root Mean Squared Error): MSE の平方根
• 決定係数: 相関の強さの2乗

# 評価
# MAE
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(Y_test, predict_lr)
print("MAE:{}".format(mae))

# MSE
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(Y_test, predict_lr)
print("MSE:{}".format(mse))

# RMSE
rmse = np.sqrt(mse)
print("RMSE:{}".format(rmse))

# 決定係数
print("R^2:{}".format(model_lr.score(X_test, Y_test)))

#評価結果
MAE:3.544918694530246
MSE:23.394317851152568
RMSE:4.83676729346705
R^2:0.7279094372333412

決定係数が約 0.73 のモデルを作成できました。

6. 展開

ビジネス課題を解決するためにデータ分析の評価結果をビジネスに適用します。今回はモデルを作成・評価するところまでが目標ですが、実際のビジネスでは作成したモデルを用いて業務改善につなげたり、システム開発を行ったりします。

ディスカッション

実習生が実際にデータ分析を体験してみて感じた率直な疑問に対し、Lumada Data Science Lab. のメンバがお答えします。

何を外れ値として除去するか悩んだのですがどう判断すれば良いでしょうか？
箱ひげ図とヒストグラムを見てもよくわかりませんでした。

明らかにあり得ない値や、条件が特殊なレコードを除くことが目的です。これらのデータは、モデリングの結果を不用意に歪めてしまうためです。まずはデータを良く眺めることが重要です。松下さんが行ったように、箱ひげ図やヒストグラムをプロットするのも気づきを得るためによく用いられる方法です。例えば変数の値に異常な偏りがある場合、プロットすれば容易に気づくことができます。また、そのような値を取っているレコードの傾向にさらに踏み込んでみることで、背景に潜む現象や値の意味づけに気づくこともあります。

変数間の相関が強いと判断するのは、相関係数がいくつ以上の場合ですか？
もしくは別の方法で確認できますか？判断基準がよくわかりません。

相関係数が 0.7 以上で一般に相関が強いと考えられることが多いようですが、実際にはドメインによります。そのため、お客様と判断基準を議論することが非常に大切です。今回の場合は、説明変数間で相関係数が 0.9 以上の組合せに着目しましたが、相関係数だけを見るのではなく、散布図でばらつきの傾向もよく確認することが大切です。

k-fold 交差検証の cross_val_score で算出しているのは決定係数 $R^2$ ですか？

ライブラリの実装に関する情報は、API リファレンスにまとめられているので、それを参照すると良いです。質問の cross_val_score の算出指標については、引数の scoring で指定します。名前や関数で算出するスコアを指定することできます。無指定の場合には、モデリングのアルゴリズムで実装されている score 関数を利用します。LinearRegression では $R^2$ が実装されています。

k-fold 交差検証って毎回やるべきものですか？
交差検証をしない場合もあるのでしょうか。

k-fold 交差検証は一つの手段で、一般論として検証を行うことが大事です。データ量やばらつきなどの条件に応じて、hold-out 検証や k-fold 交差検証、leave-one-out 交差検証などが行われます。検証の目的は、モデルが学習に用いたデータへ過剰に適合する現象 (過学習) を検出し、未知のデータへの予測性能 (汎化性) を高めることです。母集団の統計的なふるまいを知っており、分布が明らかである場合には分布のパラメータ推定にすべてのデータを活用しても良いでしょう。

主要要因 (目的変数にもっとも影響を与える説明変数) は何を確認するべきですか？
回帰係数？相関係数？やり方は色々ありそうだけれど、何で選べきぶかよくわかりません。

重回帰モデルであれば説明変数の独立性 (多重共線性がないこと) に注意したうえで、変数の大きさや単位の違いを考慮するため、標準化した回帰係数を比較すれば良いです。多重共線性は多変数の関係を慎重に確認する必要があり、VIF (分散拡大係数) のように、ある変数を他の変数で実際に回帰して影響を評価するアプローチや、主成分回帰のように、予め相関のない変数を合成してから回帰するアプローチなどがとられます。

データ分析を一通り記述した他の方の実装を参考にしたいのです。
何か良い方法はありますか？

Qiitaを熟読するというのは言わずもがなですが、Kaggle というデータサイエンスのコンペティションを実施しているサイトがあり、Boston housingを含む様々な問題に対する Notebook (データ分析プログラム) の公開や議論が活発に行われています。他のデータ分析者がどんな方法を用いているのか、これを読むだけでもとても勉強になります。また、前提となる統計の基礎知識をつけるために、入門書を読むのも良いでしょう。

演習の感想

sklearnではデータ分析メソッドが沢山用意されているので、想像以上に順調にモデルの実装ができました。ただ、今回のように整ったサンプルデータでも、データ分析の方針では悩むことが多かったので、実際のビジネスにおけるデータ分析では、もっと試行錯誤が必要なんだろうなと想像しました。「データ分析はモデリングまでの前処理が9割」なんて言われるのも、少し分かった気がします。今回はメソッドの使いこなしがメインでしたが、演習を通じて何故その方法なのか本質まで理解して、お客様に納得感のあるデータ分析に基づいたご提案が出来るようになると良いなと考えています。

おわりに

今回は実習生の松下さんにボストン住宅価格問題 (Boston house prices dataset) に取り組んで頂きました。ディスカッションでは、外れ値や相関や検証に関する考え方など有意義な議論ができたかと思います。Lumada Data Science Lab.では、これからも様々な実習記事を投稿していきたいと考えていますので、次回の投稿をどうぞご期待下さい。ここまで読んで頂き、ありがとうございました。