ベイズ×Factorization Machines & Matrix Factorizationの研究まとめ

はじめに

今回は、Factorization Machines(FM)やMatrix Factorization(MF)とベイズを絡めた研究を調べたのでまとめていきたいと思います。

FMはICDM2010で提案されて以来、様々な方向に発展しています。
Deepと組み合わされた研究や、Fieldという概念を加えた研究などがその一例です。

実際、ICDM2010でもっとも引用されている論文がFMだそうです。すごいですね。
モデル自体がシンプルで扱いやすく、特徴量が色々入れられるなど、メリットが大きいことが理由の一つかと思います。

今回の記事では、SIGIR2019 で発表されたBayesian Personalized Feature Interaction Selection for Factorization Machines [Chen+, SIGIR2019]という論文に至るまでの流れを、
FMとベイズと組み合わせている研究という切り口で紹介していこうと思います。

FMとベイズの組み合わせを調べていると、FMの一部であるMFとの組み合わせが先に提案され、それをFMに適用した、という流れが多かったので、本記事でもMF→FMの順に論文を紹介していこうと思います。

最後に紹介するBayesian Personalized Feature Interaction Selection for Factorization Machinesを中心にまとめていくつもりなので、他の文献は軽めに、今回の主役の論文は詳しめに説明していこうと思いうので、時間がない方は最後の論文だけ読んでもらえればと思います。

Probabilistic Matrix Factorization (PMF) [Salakhutdinov+, NeurIPS2007]

MFの持つ問題点である、

• データサイズに対してスケールしない
• ratingが少ないuserで失敗しがち

という二点に対して改善を行った研究です。

PMF自体は単純にMFを確率モデルにしただけ(embeddingが従う分布を仮定)で、この確率モデルについてMAP推定すると正則化つきMFに一致するのでこれだけだとあまり新しくないですが、
これに加えて、本論文では2つのバリエーションを提案しています。

• PMF adaptive : embeddingの従う分布のパラメータの事前分布を導入してそれごと最適化
• constrained PMF : ratingが少ないuserのために、似たitemにratingつけたuserは似ているという制約を導入

PMF adaptiveでは、embeddingの従う分布のパラメータの事前分布を導入して、それごと最適化することで、正則化係数の部分にあたる事前分布の分散パラメータ自体も自動で学習することを可能にしました。
モデルの複雑度自体もデータから自動で推定しよう、という試みです。

constrained PMFでは、商品評価の少ないuserに対して上手く予測を行うために、事前分布に制約を加えています。

ただ、この論文では全て結局はMAP推定していて、事後分布自体を求めている訳ではない部分が未解決として残りました。(MCMCなどでやれば性能向上が見込めるがコストがかかるのでやってない)

PMFについてはこちらが参考になると思います。

論文紹介：Probabilistic Matrix Factorization - Speaker Deck

Bayesian Probabilistic Matrix Factorization (BPMF) [Salakhutdinov+, ICML2008]

前項のPMF adaptiveと同じ考え方で、hyperparameterにも事前分布を与えています。
次のようなグラフィカルモデルになります。
左が普通のPMFで、右側がBPMFです。

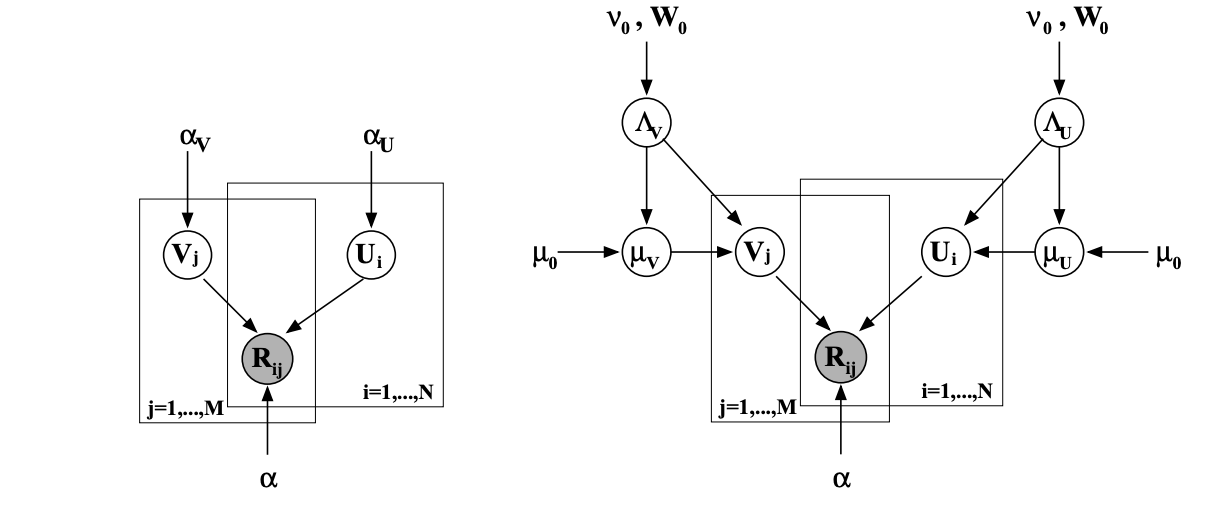
こちらはMAP推定ではなくMCMCを用いて事後分布の情報を得ています。

変分近似は過度にシンプルにすると失敗するので今回はMCMC(のなかのギブスサンプリング)を使ったそう。

user embedding, item embeddingのそれぞれのhyperparameter(ガウス分布の平均と精度)を交互に条件付けてギブスサンプリングしています。

サンプル列から予測分布を作るのは書いてあったけど、実際に何を予測に用いているか特に書いていないように見えた。
下で紹介しているブログの実装では、サンプルしたembeddingの内積とって平均したものを予測に使っていました。

BPMFについてはこちらがわかりやすいです。

Bayesian Probabilistic Matrix FactorizationをJuliaで実装 - Deep Karmaning

BPMF(Bayesian Probabilistic Matrix Factorization)によるレコメンド - LIVESENSE Data Analytics Blog

BPMFのFMバージョンがこちらです。

Bayesian Factorization Machines (2011)

Sparse Probabilistic Matrix Factorization (SPMF) [Jing+, IJCAI2015]

PMFの問題点

• sparse
• long tailed

を、embeddingの従う分布のパラメータの事前分布をガウス分布からラプラス分布にして解消した、という研究です。

ラプラス分布はガウス分布と比較して０のところで大きく、裾も厚い分布をしています。

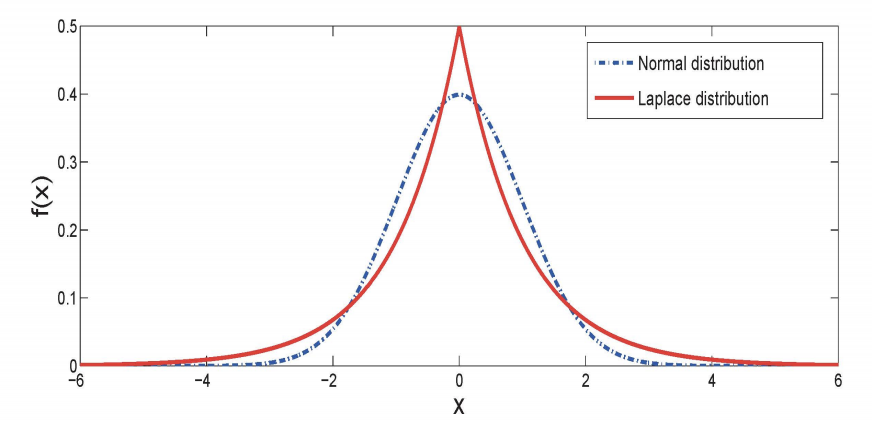
これを事前分布に用いることで、重要なところ以外は0になりやすいようなembeddingを学習できる、という気持ちが入っています。
予測に効きそうな特徴量だけうまく選択したい、ということで特徴量選択の問題に取り組んでいる研究です。
少し話が逸れますが、feature selectionの手法は二種類に大別され、

• wrapper methods:いくつか特徴量を試して重要そうなものを使う。modelに依存しないけどスケールしないという弱点あり
• embedded methods: model学習時に一緒に特徴量選択を行う。SFMや本手法はこの流れ

があるそうです。あまり詳しくないので今後勉強したいです。

で、話を戻すと、ラプラス分布を使うと解析的に計算するのが難しくなるのでは、と思うのだけど、なんかうまくできるらしい。うまいことやると条件付き分布が導出できるので、ギブスサンプリングできる、ということが書かれていました。

Sparse Factorization Machines (SFM) [Pan+, ICDM2016]

SPMFのFM バージョン。
上手いことやるというところまでほぼ同じ。

SFMと調べたらこれだけかと思ったら、他にもSFMがあるらしいです。これもSparse Factorization Machinesで、目的も同じく予測に効きそうな特徴量だけ使いたい、ノイズを入れたくない、みたいな目的で一致していましたが、
眺めた感じではベイズでもないみたいなので、今回は詳しく書きませんでした。

Synergies that Matter: Efficient Interaction Selection via Sparse Factorization Machine (SDM2016)

BP-FIS for Factorization Machines [Chen+, SIGIR2019]

いよいよ真打ち登場。

この論文では、SFMをpersonalizeするということをやっています。
予測に効きそうな特徴量の組は、userごとに異なるはずだから、そこも考慮したモデルを作らないとだよね、というモチベに基づいた研究です。

パッと思いつくのは、userごとに個別のSFMを作るという手法ですが、これは時間やストレージのコストが大きい、協調フィルタリングの良さを活かせないからという理由であまりよくありません。

論文ではまず、personalized FMを定式化しています。
FMをuser分用意しています。

(オリジナルのFMはuser idを入力に用いることでpersonalizedな予測をしていますが、これだとuser以外の特徴同士のinteractionをpersonalizeができないので、今回やりたいpersonalizedな変数選択できる形になっていないため、personalized FMの定式化が必要、とのこと)

user $u$についてのpersonalized FMを次のように定式化します。

\hat r_u(\boldsymbol x) = b_u + \sum_{i=1}^d w_{ui}x_i + \sum_{i=1}^d \sum_{j=i+1}^d w_{uij}x_ix_j

FMは$w_{uij}$をベクトルの内積にfactorizeするのが普通ですが、とりあえずは$w_{uij}$はこのままで扱い、あとでfactorizeします。

このままuserごとにFMを学習しては協調フィルタリングの良さが失われてしまうので、重み$w_{ui}, w_{uij}$を次のように分解します。

w_{ui} = \tilde w_{i} s_{ui}, \\
w_{uij} = \tilde w_{ij} s_{uij}

重みを$s$と$\tilde w$の積に分解しています。$s$はuser依存、$\tilde w$は全userで共通で学習、ということです。
$s$は0か1をとる確率変数で、ベルヌーイ分布を仮定しています。
$s_{uij}=0$だったら、user $u$がfeature $x_i$と$x_j$を予測に用いない、というようなことができます。
$\tilde w$の方はガウス分布を仮定しています。
特徴量選択をuserごとに可能にしつつ、重みは共通して学習することで協調フィルタリングぽさも活かしています。
このようなモデル化に使っている事前分布をspike-and-slab priorと呼ぶらしいです。
今回はFMの特有の構造に適したモデル化として、Hereditary spike-and-slab priorを提案しています。

Hereditary spike-and-slab priorを考えるにあたって、$s_{ui}$と$s_{uij}$には階層関係があると考えるのが自然です。
例えば、user $u$がfeature $x_i$も$x_j$も重要でないので予測に用いないのに、$x_{i}x_{j}$の交互作用項は予測に用いる、ということは考えづらいです。
なので、$s_{ui} = s_{uj}=0$なら$s_{uij}=0$であってほしい、などの階層関係が入れられると自然です。

この研究では、以下の仮定を置いてモデルを作っています。

• strong heredity : $s_{ui}$と$s_{uj}$が選ばれていたら$s_{uij}$も選ぶ
• week heredity: $s_{ui}$と$s_{uj}$のどちらかが選ばれていたら、$s_{uij}$は0ではない確率で選ばれる

こうすると、自然な構造を保ちつつパラメータの個数が減ってくれるというわけです。
このようにモデル化した後、事後分布を求めます。
解析的に求めるのは大変なので、変分近似しています。

変分近似分布は、$\tilde w$の方をガウス分布、$s$をベルヌーイ分布と仮定して分解してELBO最大化します。
ガウス分布の変分パラメータはVAEのようにReparameterization trickを使って勾配を取れるようにします。
Reparameterization trickはVAEについて書かれているここ
などを見ていただければと思います。
ベルヌーイ分布の変分パラメータは勾配を取るのが難しい($s$が離散なので)ので、[1611.01239] Reparameterization trick for discrete variables
を参考に、積分消去しています。

さて、最後に後回しにしていたFMっぽく$w_{uij}$をfactorizeする話ですが、
このモデルでは変分パラメータである$\pi_{uij}, \mu_i, \sigma_i$を以下のように分解しています。

• $s_{uij}$の従うベルヌーイ分布の変分パラメータを$\pi_{uij}$= $\pi_{ui} \pi_{uj}$と分解

• $\tilde w_{ij}$の変分パラメータ(ガウス分布の平均$\mu_i$,分散$\sigma_i$)を　$\mu_i= \boldsymbol\mu^{\top} f_{\phi}(\boldsymbol v_{i} \circ \boldsymbol v_{j})$ , $\sigma_i= \boldsymbol\sigma^{\top} f_{\phi}(\boldsymbol v_{i} \circ \boldsymbol v_{j})$　と分解

関数$f_{\phi}$のところを恒等関数にしたりdeepにしたりしてモデルを改造できるようにしています。
実験ではBP-FM (恒等関数) BP-NFM(DNN)を試しています。

おわりに

今回はFactorization MachinesやMatrix Factorizationとベイズを組み合わせた研究を、Bayesian Personalized Feature Interaction Selection for Factorization Machinesを中心に見てきました。

冒頭でも書きましたが、FMについてはたくさんの派生研究があり、様々な切り口からその流れを辿れるのが面白いと感じます。(し、FMの知識を手がかりにすることで、FMと組み合わされる側の分野の勉強もできてお得感?があります。)

参考にしていただければ嬉しいです。最後まで読んでいただきありがとうございました。

参考文献

• [Chen+, SIGIR2019] Yifan Chen et al. "Bayesian Personalized Feature Interaction Selection for Factorization Machines" SIGIR, 2019.
• [Salakhutdinov+, NeurIPS2007] Ruslan Salakhutdinov et al. "Probabilistic Matrix Factorization" NeurIPS, 2008.
• [Salakhutdinov+, ICML2008] Ruslan Salakhutdinov et al. "Bayesian Probabilistic Matrix Factorization using Markov Chain Monte Carlo" ICML, 2008.
• [Jing+, IJCAI2015] Liping Jing et al. "Sparse Probabilistic Matrix Factorization by Laplace Distribution for Collaborative Filtering" IJCAI, 2015.
• [Pan+, ICDM2016] Zhen Pan et al. "Sparse Factorization Machines for Click-through Rate Prediction" ICDM, 2016.