はじめに
今回は、協調フィルタリング(Collaborative Filtering)とMetric Learningを組み合わせたCollaborative Metric Learning (CML)とそこから発展したいくつかの論文を読んだので、まとめていきたいと思います。
割と新しめな研究だからか、あまり日本語の記事がヒットしないなと感じました。
オンラインでの計算量が大きくて大変なところを近似的に解くことで高速化できるのは魅力的だと思うので、この記事を通して興味を持ってもらえたらと思います。
Metric Learningについてはほぼ初心者なので、何かありましたらコメントいただけると嬉しいです。
よろしくお願いします。
Metric Learningについてはこの辺りを参考にさせていただきました。
Collaborative Metric Learning (CML) [Hsieh+, 2017]
- Collaborative Metric Learning(WWW 2017)
Collaborative Metric Learning (CML)が初めて提案された論文です。
以前から似たようなアイデアの研究はあったそうなのですが、explicit feedbackではなくより実用的なimplicit feedbackでの問題設定であること、Collaborative Metric Learningという名付け、定式化などがこの論文でなされており、引用されるのもこれがスタンダードなようなのでこちらをはじめに紹介します。
協調フィルタリングの問題点
協調フィルタリングの例としてシンプルなMatrix Factorizationをあげて説明します。
Matrix Factorizationなどの手法では、userとitemをある同一の空間に埋め込み、 それらのembeddingの内積によりuserがitemを好むかどうかを表現しています。
このようにして得られるuserとitemのembeddingは、userがitemを好んでいる場合、正しく学習されれば近い場所に埋め込まれるはずです。
では、似たようなuser同士や、似たようなitem同士は近くに埋め込まれるのでしょうか? 必ずしもそうはならない、というのが本論文の主張です。
論文中にある次の図を見てみます。
左がMatrix Factorizationなどの内積を用いた場合のembedding,右が今回提案するようなmetic learningを使って得られる(得られてほしい)embeddingを可視化した図です。
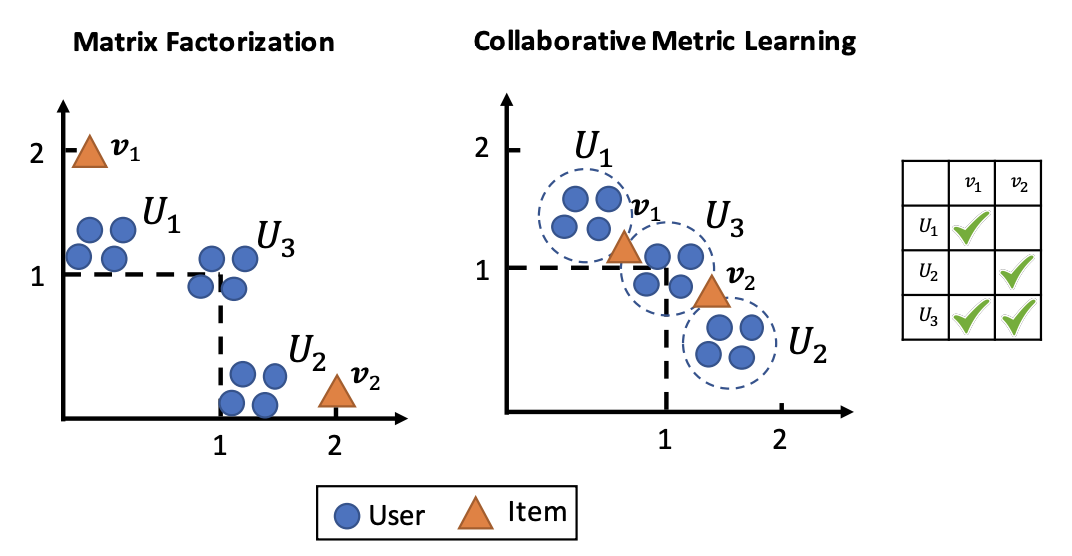
User group $U_1$はitem $v_1$を、User group $U_2$はitem $v_2$を、
User group $U_3$はitem $v_1, v_2$の両方を好む場合です。
user $U_3$がitem $v_1, v_2$の両方を好んでいるのである程度$v_1, v_2$は似ているはずなのに、$v_1, v_2$の内積を計算してみると0となってしまい、類似していないことになります。
図を見ると、$v_1, v_2$が離れた場所に埋め込まれていますね。
これは、内積が三角不等式を必ずしも満たさないために、user $U_3$が両方のitem $v_1, v_2$を好むという情報が$v_1, v_2$同士の類似度まで伝搬していないということです。
本当は右図のように、$v_1, v_2$のembedding同士が近くなってほしいよね、というのがCMLのやりたいことです。
提案手法
CMLでは、implicit feedbackでの問題設定を考えます。
implicit feedbackはクリックや購入履歴といったfeedbackを指し、正例のみが得られる(観測されないuser,itemのペアだからと言って必ずしもrelevantでないという訳ではない)点が特徴的です。
CMLでは、userのembeddingに対し、このuserと共起した(購入やクリックされた)itemを近くに、共起していないitemを遠くに埋め込むように学習します。
metric learningでいうtriplet lossのような考え方を使っているわけですね。

ただ、従来のmetric learningでは似ているもの同士を近づけ(pull loss)、似ていないものを遠ざける(push loss)ようにlossを設計するのですが、CMLでは少し異なります。
今回の問題設定ではitemに対して共起するuserが多すぎる(あるitemはたくさんのuserに購入される)と考えられます。このため、あるitemを共起した全てのuserに近づけることはできません。そのためpull lossは入れずに、共起したペアとしていないペアで相対的に近い/遠いといった関係を学習します。
学習したembeddingを用いてuserにitemを推薦するには、userの近傍のitemを探索するのが一番シンプルでしょう。ここで近似最近傍探索を使うことにより高速化できたりするメリットもあります。
詳細はこちらに紹介記事を書いたので、よろしければ参考にしてみてください!
【論文紹介】Collaborative Metric Learning (WWW2017)
以降、CMLから発展した研究をいくつか紹介します。
Latent Relational Metric Learning (LRML)[Tay+, 2018]
- [1707.05176] Latent Relational Metric Learning via Memory-based Attention for Collaborative Ranking(WWW 2018)
CMLでは、共起したuserとitemのembeddingを近づけ、それ以外は遠ざけるように学習していました。
このため、userと共起したitemを全て同じ点に埋め込もうとしてしまい、埋め込む先の空間上で制限的である、という欠点があると論文中で指摘されています。userとitemは多対多なので、理想的な埋め込みを得るのは確かに難しい気もします。
同一の点に埋め込むかはさておき、CMLが得ようとしているembeddingの制約と、embeddingの変数の個数を比べると、観測データが増えるごとに近づけなければならないペアが増えるので制約の方が多くなり、問題が退化するような状態に陥ると考えられます。
この論文では、Latent Relational Metric Learning (LRML)という、共起したuserとitemをそのまま近づけるのではなく、userのembeddingにrelationベクトルを足したものがitemのembeddingに近づくように学習する手法を提案しています。

relationベクトルの計算にはuserとitemのembeddingを入力とするMemory-basedなAttention機構を使っています。Attentionの構造はとてもシンプルなものを使っている印象でした。
Attentionの計算部分に追加したパラメータのおかげで表現力が増し、論文中で指摘されているill-posedな問題という点がある程度緩和されるのかな、と感じました。
こちらも記事を書いています。
Collaborative Translational Metric Learning (TransCF)[Park+, 2018]
LRMLと似ていて、userのembeddingにtranslationベクトルを足してitemのembeddingと近くなるように学習します。translationベクトルはLRMLのrelationベクトルと似たようなものですが、LRMLはAttention機構を援用して作っており、こちらは追加のパラメータを用いないという点で違いがあるようです。
具体的なtranslationベクトルの作り方は、
userやitemのembeddingの共起したembeddingの平均ベクトルをそれぞれ作って、それらの要素積をtranslationベクトルとしています。
\boldsymbol \beta^{nbr}_i = \frac{1}{|N_i^{\mathcal u}|}\sum_{k \in N_i^{\mathcal u}} \boldsymbol \alpha_k
\boldsymbol \alpha^{nbr}_u = \frac{1}{|N_u^{\mathcal I}|}\sum_{k \in N_u^{\mathcal I}} \boldsymbol \beta_k
\boldsymbol r_{ui}=f(\boldsymbol \beta^{nbr}_i, \boldsymbol \alpha^{nbr}_u)
$f()$を他の関数にしてもいいですが、論文中では要素積を用いています。
LRMLのrelationベクトルはuserとitemのembeddingを入力とするAttention機構によって計算されていましたが、こちらは入力それ自体は用いず、入力であるuserやitemと共起したitemやuserのembeddingを用いているところが異なります。
(おそらくLRMLもだけど)TransCFはintensityとheterogeneityをうまく扱おうというモチベーションの研究です。
userを単一のembeddingに埋め込むのでは、各itemへのrelevanceの強度が異なること、itemのカテゴリーごとに作用の仕方が異なることなどをうまく表現できないはず、というのがメインのアイデアとなっています。
論文中では、実際に解きたいタスクのデータセットを用いた事前実験によって、これらintensityとheterogeneityが存在することを確認しています。
また、userとitemのembeddingをそのまま近づけるのではなく、translationベクトルを足した時の距離を考えるようにしたため、CMLで使わなかったpull lossを復活させているのも面白いなと感じました。
CMLではあるitemがたくさんのuserと共起するので、それら全てをpullすることは難しいのでpull lossは削除し、push lossのみ採用していたわけですが、今回はtranslationベクトルのおかげでpull lossを入れても動きそうだよね、という考えです。なるほど。
Memory Network for Multi-Relational Recommender Systems (MRMN)[Zhou+, 2019]
- [1906.09882] Collaborative Metric Learning with Memory Network for Multi-Relational Recommender Systems(IJCAI 2019)
複数のfeedbackが得られた場合のLRMLに相当します。例えばクリックした、購入した、サイトに訪れた、SNSに共有した、など複数種類のfeedbackが存在する場合です。

feedbackの種類ごとにrelationベクトルを作る部分がメインの貢献かなと思い、詳細は省略です。
気になった方は読んでみてください。
Improving Collaborative Metric Learning with Efficient Negative Sampling [Tran+, 2019]
ここまではuser embeddingに何らかのembeddingを足して動かしてみよう、という研究が続いていましたが、こちらは趣向が変わってサンプリングを工夫した研究です。
CMLでは観測されていないuserとitemの組(遠ざける方のペアですね)をサンプリングする時、一様サンプリングしていましたが、この手法では小さいバッチサイズの時に性能が悪化するという問題点を指摘しています。
この論文では、popularity biasとこの問題の二つを解決する二段階サンプリングを提案しています。
一段階目では、人気度(logに出現する頻度)に応じて複数のitemをネガティブサンプリングしてきます。
Pr(j) = \frac{f(j)^\beta}{\sum_{j'}f(j')^\beta}
$f(j)$がitem $j$のlogに出現した頻度です。
ハイパーパラメータ$\beta$によってサンプリングの傾向が変わりますが、$\beta$を正の値にすると、観測されたitemほどよくネガティブサンプリングされやすくなります。これによってpopularity biasを低減する狙いがあります。一様にサンプリングする場合だと人気のitemが近くに埋め込まれやすいという問題があるので、一段階目のサンプリングではこの問題にアプローチしているというわけですね。
二段階目では、一段階目で絞ったitemの候補からより学習に効きそうな負例を選びます。
正例のitem $i$との内積が大きいほど高い確率でサンプリングされるようにしています。
これは二つの目的があるらしく、
- 勾配の分散の幅がsemi-hardなtripletサンプリングよりも大きくなる
- lossが大きくなる(より難しいデータ)
より学習に効きそうな負例を持ってくるという目的に合っています。
この論文ではサンプリングの他に、Global Orthogonal Regularizationというものも提案しています。
得られるembeddingが散らばるように正則化をかける感じです。
この辺りはmetric learningを詳しく勉強すると気持ちがもっとわかるのかなと感じています。
勉強したい。
おわりに
今回は、協調フィルタリングとmetric learningを組み合わせたCollaborative metric learning (CML)とそこから派生した研究をいくつか紹介しました。
自分でも協調フィルタリングの手法(Factorization Machinesなど)を使ってみたりするのですが、得られたembeddingを可視化してみると、user-userやitem-itemといった、直接内積を取らないembedding同士の関係って必ずしも正しく伝搬しないんじゃね?と思い、調べた結果CMLにたどり着いたという経緯です。
こちらの記事ではうまくいった例を載せたのですが、実験した中にはcapo-capoやchord-chordの関係が予想と違うような配置に埋め込まれていたりしたものもあり、協調フィルタリングの手法において三角不等式が成り立たない例を身をもって体感したといった次第です。
最後まで読んでいただきありがとうございました。
参考文献
- [Hsieh+, 2017] Cheng-Kang Hsieh et al. "Collaborative Metric Learning" WWW, 2017.
- [Tay+, 2018] Yi Tay et al. "Latent Relational Metric Learning via Memory-based Attention for Collaborative Ranking" WWW, 2018.
- [Park+, 2018] Chanyoung Park et al. "Collaborative Translational Metric Learning" ICDM, 2018.
- [Zhou+, 2019] Xiao Zhou et al. "Collaborative Metric Learning with Memory Network for Multi-Relational Recommender Systems" IJCAI, 2019.
- [Tran+, 2019] Viet-Anh Tran et al. "Improving Collaborative Metric Learning with Efficient Negative Sampling" SIGIR, 2019.