DPP (Determinantal Point Process, 行列式点過程) の理論と、推薦システムの多様性向上への挑戦

この記事では、推薦システムにおける多様性の問題と、それを解決する手法の一つであるDeterminantal Point Process（行列式点過程）について解説します。まずDPPの理論的な概要を説明し、その後推薦システムへ適用した論文を紹介します。

導入

推薦の多様性とは何か

近年の機械学習関連技術の発達により様々な驚くべき機能が実現されていますが、その主な活用先の一つに「推薦システム」があります。

推薦システムはAmazonやYouTubeに代表されるように、商品や動画などのコンテンツ情報と、ユーザのこれまでの行動履歴を元に、大量にあるアイテムの中からユーザが興味を持ちそうなアイテムを選び取るようなシステムです。うまい推薦システムを構築すれば、ランダムなアイテムや共通のランキングを提示するよりもユーザの興味を引く確率が高まり、売上等にも大きく貢献できるということで、多くのWebアプリケーションに導入されています。

Youtubeに表示されている各種レコメンド（こちらより）

推薦システムのスタンダードな手法は、「何らかのモデルでユーザとアイテムの関連度スコア（興味のある度合い）を算出し、そのスコアが高い順に提示する」というものです。例えばユーザにおすすめのアイテムを10個推薦する場合、そのユーザに関して関連度スコアが高いアイテムTop 10をリストとして並べることになります。

しかし、この方法には欠点があります。それは、選ばれた推薦リストのアイテムに似たようなものが含まれがちだということです。アイテムAとアイテムBが似た性質を持っている場合、アイテムAの関連度スコアが高いならば必然的にBの関連度スコアも高くなるため、両方とも最終的な推薦アイテムの中に含まれるはずです。

例えば動画サイトのおすすめ欄に出てくるアイテムがほとんど同じ内容の違う動画だったらどうでしょう？確かにユーザはその動画に興味があるかもしれませんが、たいてい1つか2つ見れば十分なので、Top10で全て似たような動画を提示するのは冗長です。10枠の中にもっと幅広い種類の動画を出してあげた方が、ユーザが新たなジャンルの動画を発見するのをサポートできますし、何よりユーザの動画視聴量や満足度が上がって売上を増やすこともできるでしょう。

ただし、むやみやたらに多様なアイテムを出してしまえば、ユーザがあまり興味のないアイテムもたくさん提示することになり、逆に売上や満足度は下がってしまうかもしれません。このバランスをどう取ればいいのでしょうか？

MMR: 代表的なre-ranking手法

両者のバランスをとるための代表的な手法として MMR (Maximal Marginal Relevance) があります。

ある推薦システムにおいて、既に何かしらの第一段階モデルによってざっくりとアイテム候補が選び取られているとします。そこからさらにユーザへ提示するアイテムを絞り込んで並べることを re-ranking といいます。MMRはre-rankingを実現する手法と言えます。

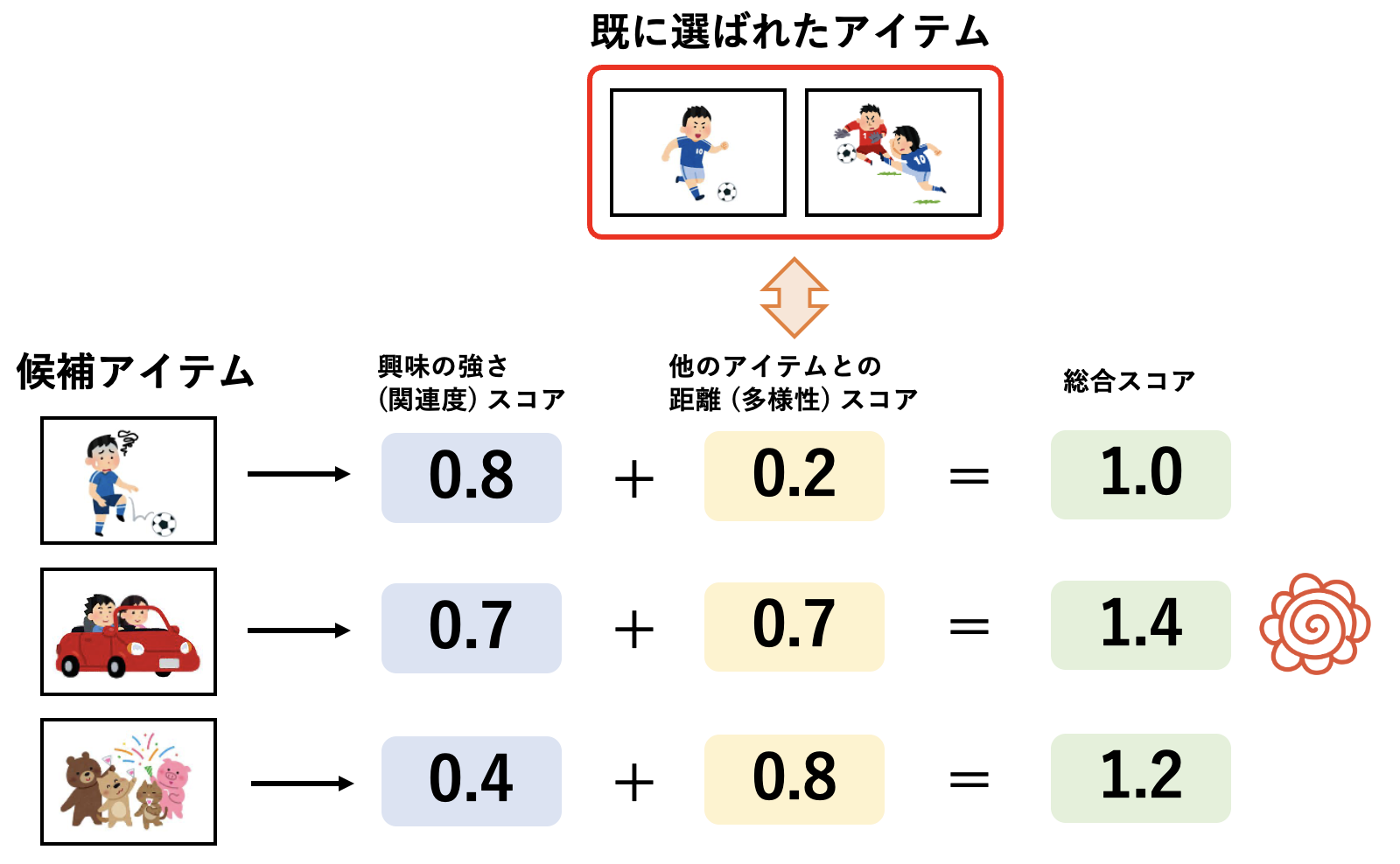
既にいくつか選ばれることが決まっているアイテムがあるとし、それらの集合を $R$ とします。さらにそれに追加するアイテムを追加で選びたい時、MMRは以下のスコア $q'_i$ を使います。

q'_i = \alpha \cdot q_i + (1 - \alpha) \cdot \frac{1}{|R|}\sum_{j \in R} dist(i, j)

$q_i$ は第一段階のモデルが候補の一つであるアイテム $i$ に与えたスコア、 $q'_i$ はMMRによって計算された新たなスコアです。$dist(i, j)$ はアイテム $i$ と $j$ の何かしらの距離を表していて、既に推薦リストに含まれることが決まっている $R$ の各アイテムと、アイテム $i$ の距離の平均が第二項となっています。つまり、$q'_i$ は、元のスコア $q_i$ と、距離に関するスコアの $\alpha~(0 <= \alpha <= 1)$ に関する重み付き和となっています。

これを使うと、既に選ばれているアイテム集合 $R$ と似ているアイテムは $q'_i$ が相対的に小さくなり、逆にあまり似ていないアイテムでは $q'_i$ が大きくなります。MMRでは $q'_i$ の大きいアイテムを順に選び取る操作を繰り返すことで、関連度と多様性の両方を考慮したアイテム選択を実現しているのです。なお、このあたりまでの説明は以下の記事が詳しいです。

Diversity(多様性)のある推薦システムとは何か？ - Wantedly Engineer Blog

しかし、MMRは非常に直感的な手法である反面、 $\alpha$ の値が性能に大きな影響を及ぼしますし、 $q_i$ や $dist(i, j)$ によって性能の良し悪しが簡単に変動してしまいます。

この記事では、複数の論文でMMRよりも性能が良いと報告されている DPP という手法について解説していきます。

DPPの理論的な話

Determinantal Point Processes（行列式点過程） は推薦や機械学習に限ったトピックではありませんが、DPPの手法を機械学習に適用することを提案した記念碑的な論文があります。

Determinantal Point Processes for Machine Learning (Alex Kulesza and Ben Taskar, 2012)

ここではこの論文の内容を中心に、DPPの理論と推薦多様性との関係を簡単に説明していきたいと思います。

DPPの定義

まず、最初にN個のアイテムがある状況を考え、それらの集合を $\mathcal{Y} = \{1,2,...,N\}$ と表します。そして、$\mathcal{P}$ を $\mathcal{Y}$ 上の 確率測度 とします。

確率測度とは、集合に対して成り立つ確率のようなものです。
全集合に対しては$\mathcal{P}(all~items) = 1$となることや、共通部分を持たない集合同士の確率測度が両者の和になる（足し算できる）ことなどが成り立つものです。
参考: 確率空間の定義と具体例

$\mathcal{Y}$ からいくつかアイテムを選んで構築されるサブセットは、$\phi$, $\{1\}$, $\{1, 2, 3\}$, $\{1,4,8, .. , N\}$など全部で$2^N$ 通り考えられます。
このうち任意のサブセット $A \subseteq \mathcal{Y}$ と、ランダムに選ばれたサブセット $\mathbf{Y}$ に対して $\mathcal{P}$ が以下を満たすとき、 $\mathcal{P}$ はdeterminantal point processです（定義）。

\mathcal{P} (A \subseteq \mathbf{Y}) = det (K_A)

ここで、 $K$ は何かしらの N x N 次元の行列であり、行と列の各インデックスが $\mathcal{Y}$ の各アイテムに対応しています。 $K_A$ は、 $K$ のうち部分集合 $A$ に対応する行と列のインデックスを取ってきたもので、 $K$ のサイズは $A$ に含まれるアイテム数となります。

上の定義式、言葉で説明しようとするとかなり分かりにくいのですが、 L-ensembles というテクニックを使って変形すると、以下のように書くことができるようです（証明略）。

\mathcal{P} (\mathbf{Y} = A) = \frac{det (L_A)}{det (L + I)} \propto det (L_A) ~,~ L = K(I - K)^{-1}

定義に現れた $K$ を $L$ に置き換えることにより、これは単に「サブセット $A$ が生起される確率」を表すようになりました。$L$ も N x N 次元の行列なので、要するに 「各アイテムが各行と各列に対応している何かしらの行列 $L$ があり、その部分行列の行列式が部分集合の生起確率 $\mathcal{P}$ になるとき、それがDPP」 と考えることができます。

これ以降は主に $K$ よりも直感的に扱いやすい $L$ を対象にして議論します。また、後述するように実用上興味があるのはもっぱら $\mathcal{P}$ の最大化なので、$\mathcal{P} (A) \propto det (L_A)$ という関係に主に着目していきます。

さて、「何かしらの行列 $L$ って何？」という話ですが、$L$ に関して条件があります。
$\mathcal{P}$ は確率測度なので常に0以上な必要があり、$L$ のあらゆる部分行列の行列式は非負である必要があります。そのためには、$L$ が半正定値行列（positive semidefinite, PSD）であることが求められます。

半正定値行列の部分行列は半正定値行列である。
また、半正定値行列の行列式は常に0以上になる。
参考: 半正定値行列の性質

逆に、PSDであることさえ満たしていれば、任意の行列 $L$ に対してdeterminantal point process $\mathcal{P}$ が定義できるようです。

ここまでのまとめ
あるアイテム集合があるとき、何かしらの半正定値行列 $L$ の部分行列の行列式でアイテム集合の生起確率 $\mathcal{P}$ が定義されるとき、 $\mathcal{P}$ はDPP。

※行列表記に関する注釈
行列の部分行列を表す際、ここでは基本的には $L_{i, j}$ や $L_{A, B}$ のように、行と列それぞれのインデックスもしくはインデックスの集合を添字として書きます。ただ、行と列の集合が同じ場合は、省略して $L_A$ のように書きます。

DPPと多様化の関係

それでは、DPPと多様化にどのような関係があるのでしょうか？ここではその直感的な関係を説明します。

まず行列 $L$ の対角成分について考えます。あるアイテム $i$ を1個だけを含む集合 $\{i\}$ の生起確率は明らかに

\mathcal{P} (\{i\}) \propto det (L_i) = L_{ii}

となるため、 $L$ の対角成分はあるアイテムがそれ単体で集合に含まれる確率になります。

また、DPPは行と列の各インデックスが $\mathcal{Y}$ の各アイテムに対応していると言いましたが、その自然な帰結として、非対角成分 $L_{ij}$ はアイテム $i$ と $j$ の間の類似度と定義すると扱いやすそうです。

ここで、2個のアイテム $i$, $j$ が同時に生起される確率は以下のように書けます。

\begin{align}
\mathcal{P}(\{i,j\}) &\propto det\begin{pmatrix}L_{ii} & L_{ji} \\L_{ij} & L_{jj} \\\end{pmatrix} \\ &= L_{ii} L_{jj} - L_{ij} L_{ji} \\ &= \mathcal{P}(\{i\}) \mathcal{P}(\{j\}) - L_{ij}^2
\end{align}

先に述べたように、 $L_{ii}$ や $L_{jj}$ は個々のアイテムが集合に含まれる確率、 $L_{ij}$ はアイテム同士の類似度のようなものと見ることができます。ということは、このスコアは （個々のアイテム自体の含まれやすさ）ー（アイテム同士の類似度） の形になっていて、個別のスコアが高くてあまり似ていないアイテムを選んだ時に最大となります。これは2次元の例ですが、サイズがより大きい場合この直感的な傾向は保たれるらしいです。

具体例として、平面状に散らばる点からいくつかをサンプルすることを考えます。DPPを用いて選ぶ場合（左）とそれぞれを独立に選ぶ場合（右）とは以下のようなイメージになります。ここでDPPは、行列の非対角成分を点同士の距離とし、 $\mathcal{P}$ を最大化するように点を選んでいます。DPPは点同士の類似度が大きくなりすぎないようサンプリングするため、より点が全体に散らばっているのが分かります。これは各点の間に斥力が働いているようなイメージで捉えるとわかりやすいです。

つまり、DPPを使って我々がやりたいのは、多くのアイテムの中から $\mathcal{P}$ を最大にするアイテムのサブセットを選ぶことだと言えます。

Y_{map} = arg max_{A \subseteq Y} det(L_A)

$\mathcal{P}$ は全集合の時に最大値を取ることが明らかなため、我々の関心はもっぱら、決まったサイズ $k$ 個のアイテムを選び取ることです。これは k-DPP と言われます。

ここまでのまとめ
行列 $L$ の対角成分をアイテム個別の生起確率スコア、非対角成分をアイテム同士の類似度スコアとして構築すると、 $L$ の部分行列の行列式を最大化するような問題を解くことで、いい感じに多様なアイテムのサブセットを得ることができる。

推薦システムにおけるDPP

DPPを個別のタスクに適用する際に問題となるのは、具体的にどうやって $L$ を構築したらいいのかということです。

DPPと推薦タスクの関係を探るため、 $L$ を分解します。
$L$ をある別の行列 $B \in \mathbb{R}^{N \times d}$ を使って $L = BB^T$ と分解します（一般に $d << N$ です）。
このとき、 $L$ の $ij$ 成分は $L_{ij} = \mathbf{B}_i \mathbf{B}^T_j$ となります。

さらに $B$ の各成分を、 $\mathbf{B_i} = r_i \mathbf{x_i}$ のように正規化されたベルトル $\mathbf{x_i}$ とそのノルム $r_i$ に分解してみると、 $L_{ij} = r_i r_j \mathbf{x}_i \mathbf{x}^T_j$ と書くことができます。

あらためて $C_{ij} = \mathbf{x}_i \mathbf{x}^T_j$ となるような行列 $C$ を置くと、 $L = Diag\{\mathbf{r}\} \cdot C \cdot Diag\{\mathbf{r}\}$ と書けます。$Diag\{\mathbf{r}\}$ は対角成分がそれぞれ $r_i$ の対角行列です。この結果、$L$ の部分行列の行列式は以下のように書けることがわかります。

det(L_A) = \sum_{i \in A} r^2_i \cdot det(C_A)

この数式は要するに、 $det(L_A)$ が 各アイテムに対応する正規化されたベクトル同士の内積で構築される $C_A$ と、それらのノルム $r$ を使って表現できる ことを意味しています。

ここで、推薦タスクにおいて、 $\mathbf{x}_i$ をアイテムの特徴ベクトル、 $r_i$ をユーザーとアイテムの関連度に対応させると、 $L$ は （ユーザーとアイテムの関連スコア成分）x（アイテム同士の類似度成分） に分解できていることになります。あらかじめユーザごとに候補となるアイテム集合の特徴ベクトルとそのスコアを計算しておいて $L$ を構築すれば、DPPを活用して多様なアイテムセットを選び取ることができます。

なお、$L_{ij} = \mathbf{B}_i \mathbf{B}^T_j$ のように、行列の $ij$ 成分がベクトルの内積で表されるような行列はグラム行列と呼ばれます。グラム行列は常にPSDであるという性質があるため、このように $L$ を定義すれば $\mathcal{P}$ がDPPになることを保証できるという嬉しさもあります。

グラム行列は常にPSDである
参考: グラム行列の定義と主な性質3つ

ここまでのまとめ
実際の推薦タスクでは、「各アイテムの特徴ベクトル」と、「ユーザとアイテムの関連度スコア」さえあれは、 $L$ を構築してDPPを計算できる。

DPPの計算の高速化

ここまで、DPPの理論を簡単に解説し、どのように推薦システムで使えるかを解説してきました。
行列 $L$ が構築できれば、あとは限られたアイテム個数でそれを最大化する問題を解けば良いです。ただ前述したように、可能なアイテムサブセットの組み合わせは $2^N$ 通りあり、$\mathcal{P}$ を最大化するサブセットを正確に求めるのはNP困難です。この計算は現実的ではないので、なんとか高速化したいです。

以下ではそれに関する2つの高速化手法を紹介します。

劣モジュラー性を使った近似的な最適化

高速化のため以下の性質を使います。
$\mathcal{P}$ はその定義より、 submodular function（劣モジュラー関数） です。

劣モジュラ関数とは集合関数の一種で、簡単にいうと、関数に渡される集合に1つ要素が加わった場合に増える関数の値が、もとの集合が大きくなるにつれ小さくなるような関数です。
参考: 集合関数，劣モジュラ性とは

数学的にいうと、 $A \subseteq B \subseteq Y \backslash {i}$ となるサブセット $A$ , $B$ について、 $f(A \cup {i}) - f(A) \geq f(B \cup {i}) - f(B)$ となるような $f$ のことです。

ともかく、劣モジュラー関数はよく知られた近似最適化があります。それは、最初空集合から始めて、最も行列式を大きくするようなアイテムを1つずつ選んで加えていく操作を繰り返していく方法です。式で書くと以下のように $j$ を選び取る操作を繰り返すことになります。

j = arg max_{i \subseteq \mathcal{Y} \backslash Y_g} ~det(L_{Y_g \cup i}) - det(L_{Y_g})

1つずつ貪欲に選んでいくため、最終的に得られた集合が最適である保証はないのですが、集合の拡大に対して広義単調増加するような場合であれば (1 - 1/e)-approximation が成り立つことがわかっています（少なくとも理想的な値の $(1-\frac{1}{e})$ 倍の範囲に収まるということ）。

このように逐次的にアイテムを選び取ることで計算が簡単になるため、ベーシックな計算手法として広く使われています。

コレスキー分解を使った高速化

劣モジュラー関数の性質を使った近似的な最適化によってだいぶ高速になりましたが、候補アイテム全てに対して行列式を計算する、という操作をアイテムを一つ選び取るたびに行うのはまだまだ計算コストが高いです（実直にやると $O(N^4)$ かかります）。

これから紹介する以下の論文は、これを $O(N^3)$ 、k-DPPでは $O(k^2 N)$ に減らすアルゴリズムを提案し、広く引用されています。

Fast Greedy MAP Inference for Determinantal Point Process to Improve Recommendation Diversity

まず、行列 $L$ をある行列 $V$ を使って分解します。

L = VV^T

ただこの際、コレスキー分解を用いることで、$V$ を下三角行列とすることができます。

ある行列が正定値対称行列の場合、それを下三角行列の積に分解できることをこれスキー分解と言う。
これまでのようにアイテム特徴ベクトルの積で $L$ を構築するならば $L$は対称行列になる。
また、半正定値対称行列についても一定の条件でコレスキー分解が可能らしい。
参照: Cholesky decomposition - Wikipedia

ここで、既に選び取っているアイテムの集合を $Y_g$ , これから選び取るアイテム候補の一つを $i$ とすると、$L$ に関して、それを含めた部分行列は以下の2個目のように書けます（$L$ のインデックスは各アイテムに対応するので）。さらにそれを以下の3個目のように分解していきます。

L_{Y_g \cup \{i\}} = \begin{bmatrix}L_{Y_g} & L_{Y_g, i} \\L_{i, Y_g} & L_{i} \\\end{bmatrix} = \begin{bmatrix}\mathbf{V} & \mathbf{0} \\\mathbf{c}_i & d_i \\\end{bmatrix} \begin{bmatrix}\mathbf{V} & \mathbf{0} \\\mathbf{c}_i & d_i \\\end{bmatrix} ^T

ここで、 $\mathbf{c}_i$ と $d_i$ は以下を満たすものです。

\begin{align}
\mathbf{V} \mathbf{c}^T_i &= L_{Y_g, i} \\
d_i &= L_i - \| c_i \|^2
\end{align}

上の式の両辺の行列式を取って変形すると、以下が得られます。

det( L_{Y_g \cup \{i\}}) = det(\mathbf{V} \mathbf{V}^T) \cdot d^2_i = det(L_{Y_g}) \cdot d^2_i

ここで、 $det(L_{Y_g})$ は固定なので、この行列式を最大にする $i$ を選ぶ場合は、 $d^2_i$ を最大にする $i$ を選び、新たな行列 $L_{Y_g \cup {i}}$ を構築しさえすれば良いということになります。

ということは、行列式を最大にするアイテムをインクリメンタルに選び取っていくとき、全ての行列式を計算する必要はなく、 気にするべきなのは $\mathbf{c}_i$ と $d_i$ だけということがわかります。

よって、 $\mathbf{c}_i$ と $d_i$ を効率的に計算する方法を考えます。
最初アイテムが全く選択されていない状況では, $\mathbf{c}_i = []$, $d_i = det(L_i) = L_i$が成り立っています。アイテムが選び取られてが更新されていくたびに、各 $i$ に対する $\mathbf{c}_i$ と $d_i$ も更新しなければなりません。

あるアイテム $j$ が選び取られた後、まだ選ばれていないアイテム $i$ に対して、更新後の $\mathbf{c}_i$ , $d_i$ をそれぞれ $\mathbf{c}'_i$ , $d'_i$ とすると、これらは以下を満たしていてほしいです（上の式に代入しただけ）。

\begin{bmatrix}\mathbf{V} & \mathbf{0} \\\mathbf{c}_j & d_j \\\end{bmatrix} \mathbf{c}^{'T}_i =L_{Y_g \cup \{j\}, i} =\begin{bmatrix}L_{Y_g, i} \\L_{j, i} \\\end{bmatrix}

1行目は自明として、2行目に注目すると、 $e_i = L_{ji} - \langle \mathbf{c}_j, \mathbf{c}_i \rangle / d_j$ とおいて、 $\mathbf{c}'_i = [\mathbf{c}_i, e_i]$ と書けます。
さらに上の式より、 $d^{'2}_i = L_i - | \mathbf{c}'_i | ^2 =d^2_i - e^2_i$ となることもわかります。

まとめると、更新のステップとしては以下のようになります。

1. $Y_g = \phi$, $\mathbf{c}_i = []$, $d_i = det(L_i) = L_i$ で初期化する
2. $d_i$ を最大にする $i$ （ $j$ とする）を選んで $Y_g$ に追加する
3. $j$ と上の更新式を使って、まだ選び取られていないアイテムそれぞれについて $\mathbf{c}_i$ と $d_i$ を更新する（具体的には $\mathbf{c}'_i = [\mathbf{c}_i, e_i]$ と $d'_i = \sqrt{d^2_i - e^2_i}$ の部分）。
4. 欲しい個数 $k$ に達するまでStep 2, 3を繰り返す

論文中に書かれているアルゴリズムは以下の通りです。

最後に時間計算量についても考えてみます。
1つのアイテムを新たに選び取る際、まだ選ばれていないアイテム $O(N)$ に対して、 $\mathbf{c}_i$ と $d_i$ を更新します。このボトルネックになるのは内積の計算 $O(k)$ なので、 合計では $O(kN)$ となります。
これを $k$ 個のアイテムを選び取れるまで毎回繰り返すので、全体の計算量は $O(k^2N)$ となります。

DPPの応用

DPPの使い方がわかったところで、DPPの推薦多様性の改善に使っている論文をいくつか紹介します。

Fast Greedy MAP Inference for Determinantal Point Process to Improve Recommendation Diversity (NeurIPS 2018)

こちらは上で紹介したコレスキー分解による高速化を提案したのと同じ論文ですが、それ以外にも、「アイテムとユーザの関連度」と「アイテム同士の類似度」のバランスを調整するハイパーパラメータである $\theta \in [0, 1]$ を導入して、$\theta$ を動かした時の変化を見る実験をおこなっています。

Netflix prizeという映画の評価スコアに関するデータなどを使って実験を行い、MMRなどの比較手法に対して安定して性能が向上したと報告されています。また、高速化に関する評価も行っていて、実行時間は実用上問題ない程度に改善されたとのことです。

Practical Diversified Recommendations on YouTube with Determinantal Point Processes (CIKM 2018)

こちらはYoutubeのレコメンドシステムに関する論文です。
既存の推薦システムはそのままに、後処理としてDPPを導入することにより、既存システムを変更することなく低コストで多様性を導入できると主張しています。

まず提案手法の第一段階として、RBF-kernelライクな変数変換ででDPP matrixを構築し、grid searchで最適なパラメータを探索しています。こちらは直感的に理解しやすく導入も簡単そうでした。

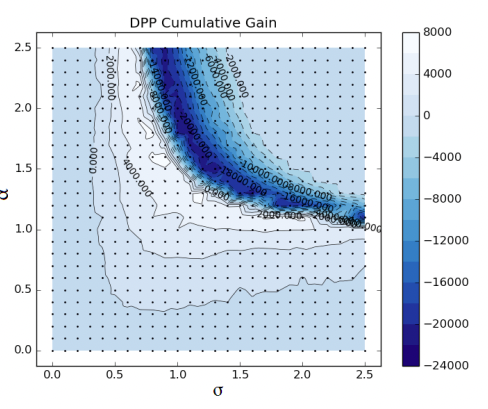
続いて、単純なNNを使った学習可能なDPPも提案しています。こちらも直感的で、上述したようにDPP matrixをユーザ特徴とアイテム特徴の成分に分解し、それぞれをシンプルなネットワークで出力しています。

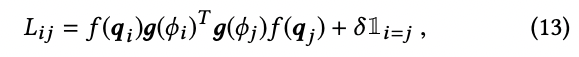
この手法は実際にYoutubeのプラットフォーム上でABtestが行われ、ユーザの長期的な満足度を向上させたと報告されています。1つ目の提案手法であるシンプルなDPPは、実際にYoutubeシステムに導入されたそうです（やや古い論文なので今どうなっているかわかりませんが...）。実験が充実しているのが好印象でした。

Determinantal Point Process Likelihoods for Sequential Recommendation (SIGIR 2022)

こちらは、ショッピングなどでユーザに次々とアイテムを提示していくようなSequential Recommendation（逐次推薦システム）にDPPを適用した論文です。

この論文の興味深いところは、推薦システムの後処理でなく、推薦モデル自体の損失関数としてDPPを導入したところです（DPP Set Likelihood loss, DSL）。以下のように、ユーザが過去に正のフィードバックを残したアイテム集合 $T^{(+)}$ と、負のフィードバックを残したアイテム集合 $T^{(-)}$ を使ってDPPスコアを計算します。
損失関数に変更を加えるだけなので、既存の手法のモデル構造を変えることなく導入できるのがメリットとされています。

Sequentialなレコメンドなので、直近にインタラクションしたアイテム集合と、今推薦候補となっているアイテムがまとまって存在しやすい確率を推定、最大化しようとしているイメージです。

推薦タスクでよく使われるMovieLensやAmazonデータセットを使って実験し、既存手法に対して提案する損失を加えた方が性能が向上することを示しています。

Diversity-Promoting Deep Reinforcement Learning for Interactive Recommendation (ICCSE 2021)

こちらは強化学習にDPP損失を導入した興味深い論文です。

まず、この記事で先に述べたように、DPPで最適化すべき行列式は以下のように「ユーザーとアイテムの関連度スコア」と「アイテム同士の類似度行列」に分解できます。

det(L_A) = \sum_{i \in A} r^2_i \cdot det(C_A)

ユーザとアイテム $i$ の関連度スコア $r_i$ は前段の推定モデルなどから与えられる場合が多いですが、この論文では $r_i = \mathbf{a} \cdot \mathbf{x}_i$ というように、アイテムベクトル $\mathbf{x}_i$ と ユーザの性質を表すベクトル $\mathbf{a}$ の内積で表すことにしています。そして、 $\mathbf{a}$ を強化学習のアクションとして捉えます。

モデルの図を見た方がわかりやすいかもしれません。

強化学習の文脈でActor-Criticモデルを学習するのですが、出てきたactionをそのまま使うのではなく、DPPの計算におけるuser vectorとして使っているイメージです。

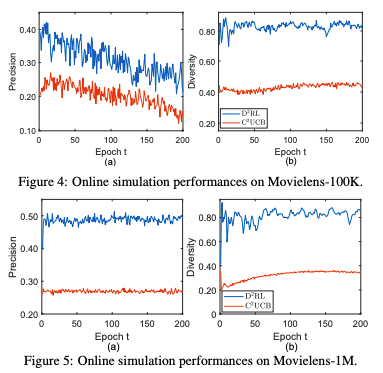
こちらもMovieLensデータセットを使って推薦性能を評価されました。
オフラインの評価ではそこまで目立った性能改善はありませんでしたが、MovieLensを使って構築したオンラインシュミレータで評価したところ、Contextual BanditモデルのC2UCBより遥かに性能が良かったと報告されています。

DPPNET: Approximating Determinantal Point Processes with Deep Networks (NeurIPS 2019)

こちらはやや独特な論文で、DPPを計算する際にmatrixを構築せずDeep networkに任せてしまう手法を提案しています。

アイテムを毎回1つずづ選び取っていくのはこれまでの手法と同じなのですが、その際、既に選び取ったアイテムとこれから選ぶアイテム候補を入力としてattention modelを学習し、出力されたprobabilityを元に選び取るアイテムを決める操作を繰り返しています。

個人的にこれがどの程度DPPの理論に即しているのかまだ理解しきれておらず、また実験で使っているデータセットも小さめなのでどの程度現実のアプリケーションに適用可能か未知数な部分があります。ただ少なくともアイデアとしては興味深い論文だと思いました。

まとめ

DPPは理論的には難解な部分もありますが、使い方は非常にシンプルで、既にYoutubeなど様々な実サービスにも適用されていることがわかりました。

推薦多様性というと売上やユーザの興味とのトレードオフと考えられがちですが、実は両者は両立可能で、多様化によって結果的にユーザのインタラクションや満足度も向上させられるのではないかと思います。

多様性万歳！！