最近データサイエンティストが多くなってきて、めでたいな~、いいことだな~と思っているのですが、多くの人は機械学習寄りの話から入っていくことが多く、統計学から入っていく人は少ないような気もします。
重回帰分析は、おそらく最も多くのデータサイエンティストと呼ばれる人達がお世話になっている手法だと思いますが、回帰診断は聞いたことすらないという人も結構多いようです。
正直、実務であまり使うことはないような気もしますし、私自身も使う機会がほとんどないのですが、復習も兼ねて勉強をし直したので、今回はそんな回帰診断について紹介したいと思います。
目次はこんな感じ。
・回帰診断とは
・前提知識(読み飛ばしてもOK)
・使うデータ(swiss)
・Q-Qプロット
・梃子比
・スチューデント化残差
・Cook距離
・まとめ
回帰診断とは
ざっくりいえば、回帰診断とは、回帰モデルの妥当性をチェックするためのツールのことです。
具体的には、ガウス・マルコフの仮定や誤差の正規性に関する妥当性、影響度の大きいデータはないか等のチェックをします。
前提知識(読み飛ばしてもOK)
◆線形モデル
今回扱うのは、線形回帰モデルです。
線形モデルというのは、$n$ 組の観測 $ \{ y_i, x_{i1},\cdots, x_{ip} \} , \ i=1,\cdots,n$ の間に
y_i = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip} + \varepsilon_i \,\,\,,\,\,\,i=1,\cdots,n \tag{1}
が成り立つことを想定するモデルのことです。
※ちなみに一般的な回帰分析の仮定では、説明変数は確率変数ではありません。固定された既知の定数であると考えます。(意外と知らない人が多いみたいなので…)
行列で表現した方が色々と便利なので、行列で表現すると、
Y=X\beta+\varepsilon \tag{2}
となります。
ここで、$Y = (y_1, \ \cdots, \ y_n)^T$ は目的変数ベクトル、$X$ は説明変数の行列(計画行列とも呼ばれます)
X = \left(
\begin{array}{cccc}
1 & x_{11} & \cdots & x_{1p}\\\
\vdots & \vdots & \ddots & \vdots \\\
1 & x_{n1} & \cdots & x_{np}
\end{array}
\right)
で、$\beta = (\beta_0\,,\,\beta_1\,,\,...\,,\,\beta_p)^T$ は、実数パラメータベクトル(係数ベクトルとも言います)。
また、$\varepsilon = (\varepsilon_1, \ ..., \ \varepsilon_n)^T$ は、誤差ベクトルです。
◆標準的な仮定
線形モデルがよく使われている理由の一つに、ガウス・マルコフの定理という、ある種の最適性を持つというのがあります。このガウス・マルコフの定理に基づいた仮定を置くのが一般的なのですが、今回もその仮定を(少しきつめに)置きます。
\varepsilon_i \stackrel{i.i.d}{\sim} N(0 \,,\, \sigma^2) \,\,\,,\,\,\,i=1,\cdots,n \tag{3}
絶対にこの仮定じゃないといけないということはないのですが、おそらくこの設定が一般的だと思うので、今回はこれでいきます。
※このように誤差の分布を仮定することによって、パラメータ $\beta$ の推定量の分布などを求められるようになり、検定などもできるようになります。(仮定する分布の中で、正規分布は最も一般的な仮定です。現実問題に対して妥当であることが多く、議論も比較的簡単で、分かりやすいためだと思われます。)
◆最小二乗法による解
パラメータ $\beta$ を最小二乗法によって推定すると、
\hat{\beta}=(X^TX)^{-1}X^Ty \tag{4}
が求まります。これを最小二乗推定量と呼びます。
また、
H = X(X^TX)^{-1}X^T
と置き、これをハット行列と呼びます。$I$ を $n$ 次元単位行列とすれば、
\begin{eqnarray}
\hat{y} &=& X\hat{\beta} = Hy \tag{5} \\
\\
\hat{\varepsilon} &=& y - \hat{y} = (I-H)y \tag{6} \\
\end{eqnarray}
が成り立ちます。
◆誤差分散の不偏推定量
誤差分散の不偏推定量 $\hat{\sigma}^2$ は以下で与えられます。
\begin{eqnarray}
\hat{\sigma}^2 &=& \frac{1}{n-(p+1)} \hat{\varepsilon}^T \hat{\varepsilon} \tag{7} \\
\\
&=& \frac{1}{\nu_e} \hat{\varepsilon}^T \hat{\varepsilon} \tag{8}
\end{eqnarray}
※最後のところは自由度 $n-(p+1)$ を $\nu_e$ で置きました。
0.使うデータ(swissのデータ)
今回はswissのデータセットを使います。
このデータセットは、1888年のフランス語圏スイス47地域の社会指標データセットです。
各変数は、
| 変数名 | 説明 |
|---|---|
| Fertility | 出生率 |
| Agriculture | 職業として農業に関わる男性の割合 |
| Examination | 被徴兵者のうち、軍事テストで最高点を取った被との割合 |
| Catholic | カトリック教徒の割合 |
| Education | 被徴兵者のうち、小学校を卒業している人の割合 |
| Infant.Mortality | 1歳未満の死亡率 |
となっています。
今回は、Fertility(出生率)を目的変数、他の変数全てを説明変数とした重回帰分析をRで行います。
### Rで重回帰分析 ###
data(swiss)
LModel <- lm(Fertility~., data=swiss) #Fertility(出生率)を目的変数とした重回帰分析
summary(LModel)
### 出力 ###
Call:
lm(formula = Fertility ~ ., data = swiss)
Residuals:
Min 1Q Median 3Q Max
-15.2743 -5.2617 0.5032 4.1198 15.3213
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 66.91518 10.70604 6.250 1.91e-07 ***
Agriculture -0.17211 0.07030 -2.448 0.01873 *
Examination -0.25801 0.25388 -1.016 0.31546
Education -0.87094 0.18303 -4.758 2.43e-05 ***
Catholic 0.10412 0.03526 2.953 0.00519 **
Infant.Mortality 1.07705 0.38172 2.822 0.00734 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.165 on 41 degrees of freedom
Multiple R-squared: 0.7067, Adjusted R-squared: 0.671
F-statistic: 19.76 on 5 and 41 DF, p-value: 5.594e-10
というわけで、
\begin{eqnarray}
Fertility = && 66.9 \\
&-& 0.17×Agriculture \\
&-& 0.26×Examination \\
&-& 0.87×Education \\
&+& 0.10×Cathoric \\
&+& 1.01×Infant.Mortality \tag{8}
\end{eqnarray}
と推定されました。
さて、ここからが本題です。
※回帰診断図自体は、
plot(LModel)
とするだけで出力することができます。順番に
A. 予測値 $\hat{y_i}$ と残差 $y_i - \hat{y}$ の散布図
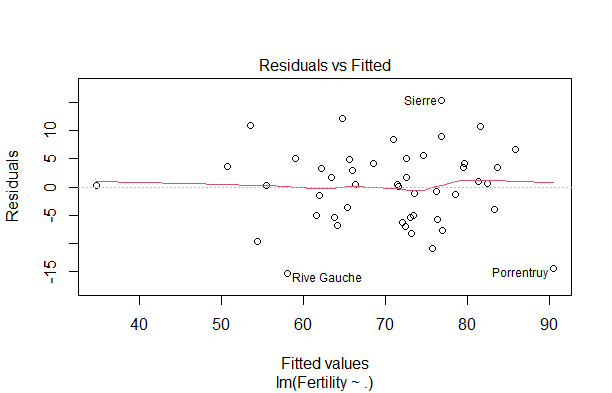
C. 予測値 $\hat{y_i}$ と標準化残差の絶対値の散布図
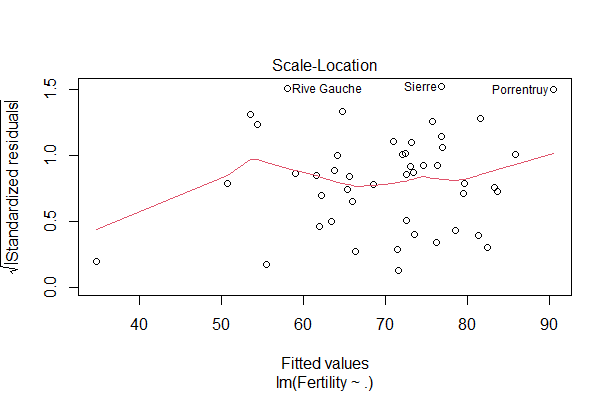
D. 標準化残差と梃子比の散布図(赤色の点線はCook距離)
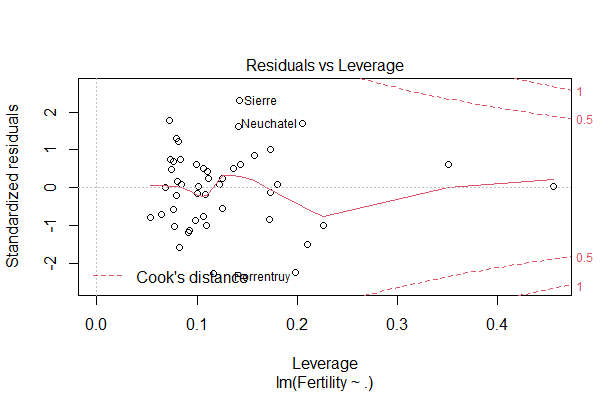
簡単ですね。
今回は勉強も兼ねてggplotを使って、図示していこうと思います。
1.誤差の正規性(正規Q-Qプロット)
ガウス=マルコフの仮定に誤差の正規性は必要ありませんが、一般的によく設定される仮定です。
正規性を仮定することにより、推定量に関する様々な議論ができるようになります。
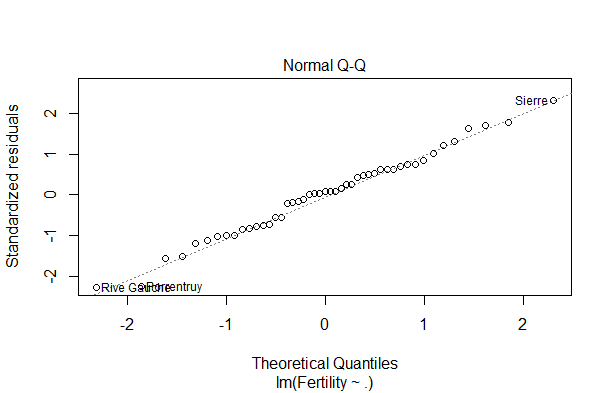
正規性を確認するには、正規Q-Qプロットが役立ちます。
※Q-Qプロットは、省略せずに書くとQuantile-Quantile plotといいます。Q-Qプロットは、2つの確率分布が似ているかを比較するための視覚的な方法です。縦軸、横軸にそれぞれの確率分布の分位数を取り、2つの確率分布が類似していれば、プロットした点が直線に並ぶというわけです。
正規Q-Qプロットは、Q-Qプロットの頭に「正規」の文字が付いていることからも分かる通り、データが正規分布に従っているかを確認します。特に回帰分析で使う場合は、残差が正規分布に従っているかをチェックします。
library(ggplot2)
LModel.resid <- data.frame(LModel$residuals) #ggplotがdata.frameしか扱ってくれないみたいなので。
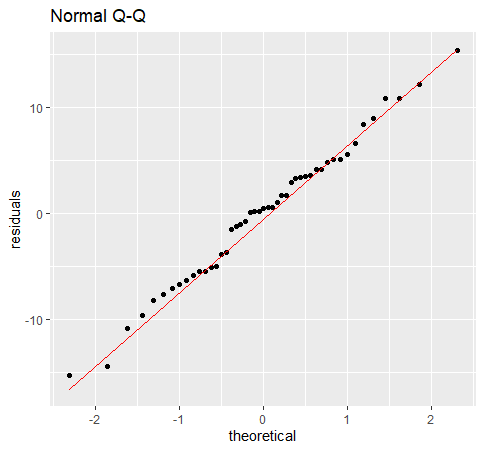
ggplot(data=LModel.resid, aes(sample=LModel.residuals)) +
geom_qq() +
stat_qq_line(color="Red") +
ggtitle("Normal Q-Q") +
ylab("residuals")
この図を見る限り、直線に乗っているような乗っていないような、、、
結構微妙ですね。
同じことをやっている書籍では、「残差の正規性に関しては疑わしい」と書いてありましたが、うーん、私の場合は正規性を容認しちゃうような気がします。
※もちろん検定も役立ちます。
正規性の検定は、それだけで1冊の本があるほど奥が深いので、ここでは割愛しますが、例えば『欠測データ処理(高橋・渡辺 2017)』P100には $JB$ 検定が取り上げられています。
$JB$ 検定の帰無仮説は、
$H_0$:誤差項は正規分布である。
であり、検定統計量は、
JB = n \left[\frac{S^2}{6} + \frac{(K-3)^2}{24} \right] \tag{9}
で与えられます。ここで、$S$ は歪度、$K$ は尖度です。
この $JB$ が漸近的に自由度 $2$ のカイ二乗分布に従うことを利用した検定らしいのですが(ちゃんと自分で確かめてない…)、カイ二乗近似が成立するためには大きなサンプルサイズが必要になるっぽいです。wikipediaによると、MATLABでは $2000$ 以上の時にカイ二乗近似を適用しているらしいです。
ちなみにRでは、
### 正規性の検定(JB検定) ###
library(normtest)
jb.norm.test(LModel$residuals)
### 出力 ###
Jarque-Bera test for normality
data: LModel$residuals
JB = 0.15512, p-value = 0.93
となり、誤差の正規性に問題があるという証拠はないという結論が得られます。
2.影響の大きいデータはないか(梃子比)
ここでは梃子比を見ていくのですが、ややこしいので少し順を追って「梃子比ってなんぞや」という部分を考えていきたいと思います。
もし、各誤差の等分散性 $V\left[, \varepsilon ,\right]=\sigma^2I$ が正しければ、残差ベクトル $\hat{\varepsilon}$ の分散共分散行列は、
\begin{eqnarray}
V\left[\, \hat{\varepsilon} \,\right] &=& V\left[\, (I-H)y\,\right] \,\,\,\,\, ∵式(6)\,:\,\hat{\varepsilon} &=& y - \hat{y} = (I-H)y \\
\\
&=& (I-H)V\left[\, y\,\right](I-H)^T\\
\\
&=& (I-H)(I-H)^T\sigma^2I\\
\\
&=& (I-H)\sigma^2 \tag{10}
\end{eqnarray}
となります。最後の変形では、$H$ の対称性と冪等性の性質を用いています。詳しくは『自然科学の統計学』のP69を参照頂ければなと思います。
個々の残差に目を向ければ、
V\left[\, \hat{\varepsilon_i} \,\right] = (1-h_{ii})\sigma^2 \tag{11}
(ただし $h_{ii}$ は $H$ の第 $(i,i)$ 成分であり、梃子比と呼ばれます。また、$\frac{1}{n}≤h_{ii}≤1$ です。)
となるので、$h_{ii}$ が $1$ に近いほど、真の $\varepsilon$ の分散 $\sigma^2$ よりも小さくなり、推定値 $\hat{y_i}$ と観測 $y_i$ が近くなると考えられます。
つまり、梃子比 $h_{ii}$ が $1$ に近ければ、推定された直線が $i$ 番目のデータに近くなります。
このことについて、式$(5)$ $\hat{y} = Hy$ を変形することで、もう少しスッキリさせてみます。
式$(5)$を変形すると、
\begin{eqnarray}
\hat{y_i} &=& H_iy \,\,\,\,\, \tag{12}\\
\\
&=& \sum_{j=1}^{n}h_{ij}y_j \,\,\,\,\, \tag{13}
\end{eqnarray}
というように予測値 $\hat{y}$ が、各観測 $y_i ,,,i=1,\cdots,n$ の線形結合で表せることが分かります。
分かりやすいようにシグマのない形で書くと、
\hat{y_i} = h_{i1}y_1 + h_{i2}y_2 + \cdots + \color{red}{h_{ii}y_i} + \cdots + h_{in}y_n \tag{13'}
です。
ということは、$h_{ii}$ が大きければ、予測 $\hat{y_i}$ に対して、その点における観測 $y_i$ が与えている影響が大きいと考えることができます。
梃子比の一般的な使われ方
梃子比 $h_{ii}$ の一般的な使われ方としては、
| 規準 | 対処 |
|---|---|
| $h_{ii} ≥ 2×\frac{p+1}{n}$ | $i$ 番目のデータを除外(異常値の懸念) |
| $0.2 < h_{ii} ≤ 0.5$ | $i$ 番目のデータは危険 |
| $0.5 < h_{ii}$ | $i$ 番目のデータを除外 |
とされています。
説明が長くなりましたが、実際にRで実行してみると、
X <- model.matrix(LModel) #モデルの計画行列
lev <- hat(X) #梃子比ベクトル。
names(lev) <- rownames(swiss) #梃子比にデータ名を対応させる。
cx <- 2 * sum(lev) / dim(swiss)[1] #異常値の閾値の計算。
#ggplot用のラベルデータを作る。
#異常知の懸念がある閾値以上の梃子比を持つデータの地域名を抽出する。
Name <- rownames(swiss)
selected_Name <- rownames(data.frame(lev[lev > cx]))
Name[!Name %in% selected_Name] <- ""
#ggplot用のデータフレーム
lev <- data.frame(c(1:47), lev)
names(lev) <- c("index", "leverage")
lev$PlotName <- Name
#ggplotでプロットする。
ggplot(data=lev, aes(x=index, y=leverage)) +
geom_point() + #点を打って
ggtitle("leverage") + #タイトルをつけて
ylab("levarage") + #yラベルと
xlab("index") + #xラベルもつけて
geom_hline(yintercept=cx, linetype="solid", color = "red") + #異常値の懸念がある閾値の線を引いて
geom_text(aes(x=index-8, y=leverage-0.02,label=PlotName), size=4, hjust=0, color="red") #異常っぽいデータにラベルを付ける。
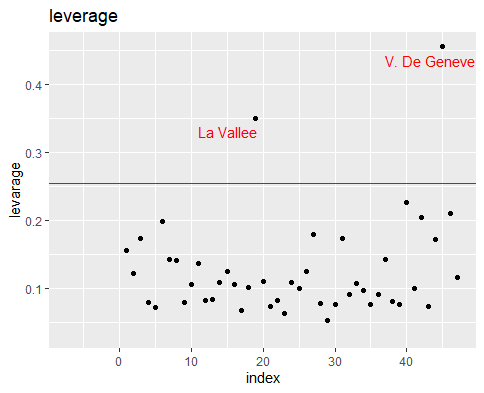
閾値は、$2×\frac{5+1}{47}≒0.255$ です。
図を見ると、La Vallee と V.De Geneve の梃子比に異常値の懸念があるっぽいですね。
具体的な値を見てみると、
lev[lev$leverage > cx,]
### 出力 ###
index leverage PlotName
La Vallee 19 0.3512078 La Vallee
V. De Geneve 45 0.4558363 V. De Geneve
というようになっています。
ただまぁ、梃子比だけを見て何かを判断するというのは正直微妙で、残差などと組み合わせてみることが多いみたいです。
例えば、梃子比が大きい場合、残差の分散は小さくなるはずです。しかし、実際に残差を見てみると、他の残差に比べて大きかったりした場合、そのデータは「おかしい…」というような判断をするようです。
今回でいうと、
### 残差と梃子比の散布図 ###
res_lev <- data.frame(lev, LModel.resid)
cx <- 2 * sum(lev) / dim(swiss)[1] #異常値の閾値の計算。
ggplot(data=res_lev, aes(x=LModel.residuals, y=leverage)) +
geom_point() +
geom_text(aes(x=LModel.residuals+0.5, y=leverage, label=PlotName), size=4, hjust=0, color="red") +
geom_hline(yintercept=cx, linetype="solid", color = "red") +
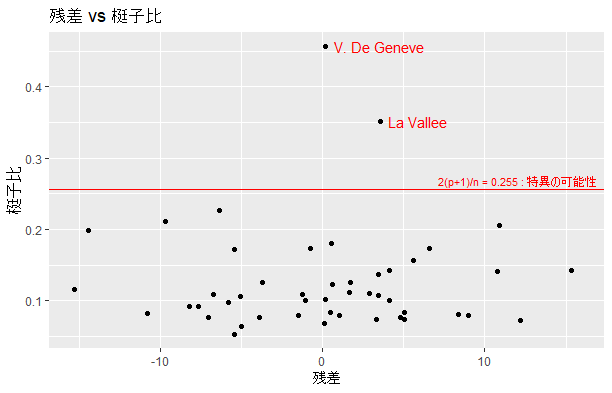
annotate("text", x=12, y=cx+0.012, label="2(p+1)/n = 0.255 : 特異の可能性", colour="red", size=3) +
ggtitle("残差 vs 梃子比") +
ylab("梃子比") +
xlab("残差")
となり、先ほどのLa ValleeとV. De Geneveは、梃子比が大きく、残差は小さいので、まぁ挙動不審というわけではなさそうです。ただ警戒しておいた方がいいということなんでしょう(解釈が難しすぎると思うけど、ほんとに使われているのか・・?)
3.残差のばらつきの一様性(スチューデント化残差)
梃子比のところでも見たように、個々のデータに対する残差の分散は、
V\left[\, \hat{\varepsilon_i} \,\right] = (1-h_{ii})\sigma^2 \tag{11}
となっています。これは $h_{ii}$ に依存しており、一様にバラついているしているとはいえないものになっています。
そこでスチューデント化残差というものを考えます。スチューデント化残差とは、次の式で定義される量です。
r_i = \frac{\hat{\varepsilon_i}}{\hat{\sigma} \sqrt{1-h_{ii}}} \tag{14}
こうすることによって、$V\left[, r_i ,\right]=1$ となり、残差そのものを見るよりも異常を発見しやすくなります。
ほんとに $V\left[, r_i ,\right]=1$ となっているのか確かめます。まず、
\frac{\hat{\varepsilon_i}}{\sigma\sqrt{1-h_{ii}}} \sim N(0,1) \tag{15}
で、また、
\frac{\hat{\varepsilon_i}^T\hat{\varepsilon_i}}{\sigma^2} \sim \chi^2(\nu_e) \tag{16}
なので、誤差の不偏分散 $\hat{\sigma}^2 = \frac{1}{\nu_e} \hat{\varepsilon}^T \hat{\varepsilon} $ を $\sigma^2$ で割ると
\begin{eqnarray}
\frac{\hat{\sigma}^2}{\sigma^2} &=& \frac{\hat{\varepsilon_i}^T\hat{\varepsilon_i}}{\sigma^2}\,\frac{1}{\nu_e} \\
\\
&=& \frac{\chi^2(\nu_e)}{\nu_e} \tag{17}
\end{eqnarray}
式(14),(16) より、
\begin{eqnarray}
r_i &=& \frac{\hat{\varepsilon_i}}{\sigma\sqrt{1-h_{ii}}} × \frac{\sigma}{\hat{\sigma}} \\
\\
&=& \frac{N(0,1)}{\sqrt{\frac{\chi^2(\nu_e)}{\nu_e}}} \sim t(\nu_e) \tag{18}
\end{eqnarray}
となります。その分散は、
\begin{eqnarray}
V\left[\,r_i\,\right] &=& \frac{\nu_e}{\nu_e-2} \\
\\
&=& \frac{n-(p+1)}{\{n-(p+1)\}-2} \tag{19}
\end{eqnarray}
となります。サンプルサイズ $n$ が説明変数の数 $p$ (定数項を含めれば $p+1$)に比べて十分に大きければ、各データにおけるスチューデント化残差の分散は $V\left[,r_i,\right]≃1$ となるというわけです。
スチューデント化残差の一般的な使われ方
スチューデント化残差の絶対値を取った時に $2$ よりも大きな値を持つものが多いと、誤差の分散の一様性を疑うというよな使い方をするみたいです。
### スチューデント化残差 ###
stdres <- data.frame(rstudent(LModel))
stdres <- data.frame(stdres)
stdres <- data.frame(c(1:47), stdres)
names(stdres) <- c("index", "Studentized_Residuals")
ggplot(data=stdres, aes(x=index, y=Studentized_Residuals)) +
geom_point() +
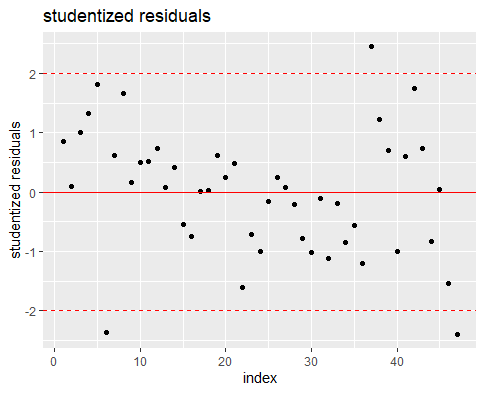
ggtitle("studentized residuals") +
ylab("studentized residuals") +
geom_hline(yintercept=0, linetype="solid", color = "red") +
geom_hline(yintercept=2, linetype="dashed", color = "red") +
geom_hline(yintercept=-2, linetype="dashed", color = "red")
図を見ると、$|r_i|>2$ となっているデータの割合は、$\frac{3}{47}≒0.064$ なので、特別多いというわけではなく、誤差の分散の一様性は、ある程度妥当だったと考えてよさそうです。
(このへんのよく使われる基準ってあるのかなあ)
※もちろん検定も役立ちます。
正直、『欠測データ処理(高橋・渡辺 2017)』P102を読むまで知らなかったのですが、誤差の分散が均一であるかを調べる $BP$ 検定というものがあります。(調べてみると経済系では割と有名っぽい??)
ちなみにRでは、
### 分散の均一性の検定(BP検定) ###
library(lmtest)
bptest(LModel)
### 出力 ###
studentized Breusch-Pagan test
data: LModel
BP = 5.8511, df = 5, p-value = 0.321
となり、誤差の分散が不均一であるという証拠はないという結果が得られます。
4.個々のデータの影響度(Cook距離)
Cook距離は、個々のデータが推定にどの程度影響したかを表したものです。
各データに対するCook距離は、次のように定義されます。
D_i^{\,Cook} = \frac{\hat{y_i} - \hat{y}_{(-i)}}{p \hat{\sigma}^2} \tag{20}
ただし、
$\hat{y_i}$ :全データを用いて得られた、目的変数の推定値
$\hat{y}_{(-i)}$ :$i$ 番目のデータを取り除いて得られた、目的変数の推定値
です。
$i$ 番目のデータにおけるCook距離が大きければ大きいほど、$i$ 番目のデータは推定に大きな影響があると判断することができます。
じゃあ、Cook距離は何がどうなると大きくなるのかということが気になると思うので、それを知るためにCook距離を少し変形してみます。
\begin{eqnarray}
D_i^{\,Cook} &=& \frac{\hat{y_i} - \hat{y}_{(-i)}}{p \hat{\sigma}^2} \tag{21} \\
\\
&=& \frac{1}{p} \, r_i^2 \, \frac{h_{ii}}{1-h_{ii}} \tag{22}
\end{eqnarray}
となります。
この式$(22)$から2つのことが分かります。
① 各観測におけるスチューデント化残差 $r_i$ が大きくなればなるほど、Cook距離は大きくなる。
② 梃子比 $h_{ii}$ が $1$ に近づくほど(大きくなるほど)、Cook距離は大きくなる。
Cook距離の一般的な使われ方
一般的には、
| 規準 | 解釈 |
|---|---|
| $D_i^{,Cook} > 0.5$ | $i$ 番目のデータは、影響度が大きめ。 |
| $D_i^{,Cook} > 1$ | $i$ 番目のデータは、影響度が異常に大きい。 |
という判断基準のようです。
### Cook 距離 ###
cook <- cooks.distance(LModel)
gg_cook <- data.frame(cook) #ggplot用にデータフレーム化
ggplot(data=gg_cook, aes(x=row.names(gg_cook), y=cook)) +
geom_col() + #棒グラフ。
theme(axis.text.x = element_text(angle = 90, hjust = 1)) + #x軸が横だと重なって見にくいので縦にする。
geom_hline(yintercept=0.5, linetype="solid", color = "red") + #影響力が大きめ(cook距離0.5)に線を引く。
annotate("text", x=38, y=0.52, label="Cook 距離 = 0.5 : 影響力大きめ", colour="red", size=3) + #線の上に文字を書く。
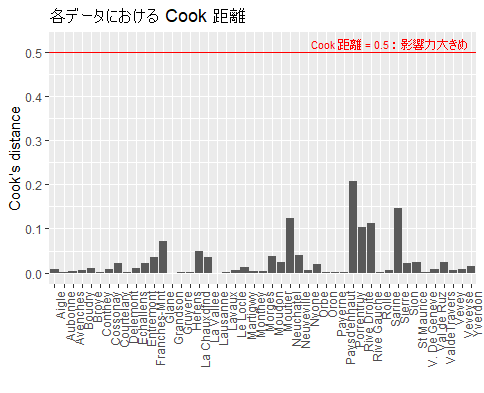
ggtitle("各データにおける Cook 距離") + #グラフタイトルをつける。
ylab("Cook's distance") + #y軸ラベル
xlab("") #x軸ラベルは邪魔だから消す。
推定に対する影響力が、大きすぎるという懸念のあるデータは、ないみたいですね。
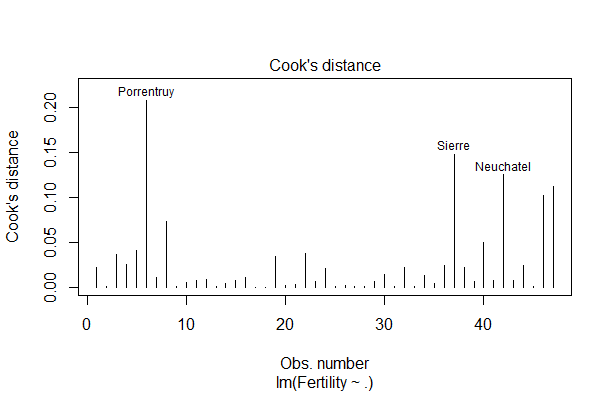
ちなみに、Cook距離の図は、
plot(LModel, 4)
#LModelは、上の方で計算した LModel <- lm(Fertility~., data=swiss) です。
とするだけで書けます↓↓
楽ちん。
まとめ
基本的なことだと舐めていましたが、勉強してみると意外と難しくて苦戦しました。
今回、取り上げたものを表にまとめると、
| 見るもの | 何が知れるか |
|---|---|
| 正規QQプロット | 誤差の正規性 |
| 梃子比 | 予測 $\hat{y_i}$ に対して、その点における観測 $y_i$ が与えている影響の大きさ |
| スチューデント化残差 | 残差のバラツキの一様性 |
| Cook距離 | 個々のデータが推定にどの程度影響したか |
というような感じになるでしょうか。
誰かの参考になれば幸いです。
★参考文献
[1] 間瀬, 神保, 鎌倉, 金藤:工学のためのデータサイエンス入門(2004)
[2] 宮岡, 野田:数理統計学の基礎(1992)
[3] 高橋, 渡辺:欠測データ処理(2017)
[4] 矢島, 廣津, 藤野, 竹村, 竹内, 縄田, 松原, 伏見:自然科学の統計学(2016)