※以下、個人的な勉強のためのレポートです。
※間違い多々あると存じますが、現在の理解レベルのスナップショットのようなものです。
※勉強のためWebサイトや書籍からとても参考になったものを引用させていただいております。
http://ai999.careers/rabbit/
AI、機械学習、ディープラーニング
AI(Artificial Inteligence:人工知能)とは、「『計算(computation)』という概念と『コンピュータ(computer)』という道具を用いて『知能』を研究する計算機科学(computer science)の一分野」を指す語[1]。「言語の理解や推論、問題解決などの知的行動を人間に代わってコンピューターに行わせる技術」、または、「計算機(コンピュータ)による知的な情報処理システムの設計や実現に関する研究分野」ともされる。
(Wikipedia https://ja.wikipedia.org/wiki/%E4%BA%BA%E5%B7%A5%E7%9F%A5%E8%83%BD#%E4%BA%BA%E5%B7%A5%E7%9F%A5%E8%83%BD%E3%81%AE%E7%A8%AE%E9%A1%9E)
AI、機械学習、ディープラーニングが混在して語られることがあるため、「人工知能ブーム」と合わせて再整理。
包含関係としては、AI ∍ 機械学習 ∍ ディープラーニング
https://markezine.jp/article/detail/29471
今話題のディープラーニング(深層学習)は、機械学習の手法の一つであり、機械学習はAIの第二次人工知能ブームの中心的存在。第一次人工知能ブームでは、コンピュータに「ルール」と「ゴール」を示してあげることで問題を解けるとしたもの。網羅的に選択枝の探索を行うことで解答にたどり着ける。しかしこれには限界があることがわかり、第一次人工知能ブームは終焉した。
https://ritsuan.com/blog/4134/
従来人間のみがこなしていた知的活動を、機械(主としてコンピュータ)に行わせる研究分野ととらえるならば、電卓だって立派なAI。しかし電卓は、入力に対してあらかじめ作成された演算ルールの結果を出力するのみ。それに対して、第二次人工知能ブームの火付け役となった機械学習は、学習する機械(マシーン)。データから学習を行い、学習した結果をモデル化する。
例えば不動産価格に関する統計データをコンピュータに読み込みませる。この統計データには、「部屋の数」「主要道路へのアクセスのしやすさ」「部屋の数」「近隣の犯罪発生率」などの諸要素が含まれる。不動産価格がどういった要素や条件により、または組み合わせの相関により影響を受け決定されるのか、統計的手法によるモデルを形成する。この形成されたモデルに、新たに不動産価格を算出したい物件の諸要素を入力すれば、モデルから算出された不動産価格が出力される。
第三次人工知能ブームを引き起こしたのが、ディープラーニング。ディープラーニングでは、学習データからマシン側が自動的に特徴を抽出する点が大きく違う。つまり、何に着目すればよいかを教える必要がなく、どんな特徴を利用すれば識別できるのかを機械が自動的に学習する。しかし逆に言えば、従来の機械学習手法はコンピュータにどのような計算を行わせたのか反証可能であり、算出されたモデルについても考察を行うことができる。対してディープラーニングにより形成されたモデルは、コンピュータがどのような経緯でそのような解を算出するモデルを形成するに至ったのかは学習の結果としか言いようがない。人間の脳を模している以上、人間の脳を開けても思考パターンはわからないように、ディープラーニングについても同様のことが言える。
https://www.sbbit.jp/article/cont1/32033#head2
https://blogs.nvidia.co.jp/2016/08/09/whats-difference-artificial-intelligence-machine-learning-deep-learning-ai/
解きたい問題が解けるのであれば、必ずしもディープラーニングによらなければならない必要はない。問題を解くためのアルゴリズムが記述できるのであれば、従来の手続きを記述するプログラミングにより可能であるし、機械学習の各種手法については、scikit-learnなどの機械学習のオープンソースライブラリ容易に入手でき、試行可能である。
https://techacademy.jp/magazine/17375
機械学習
機械学習の代表的な手法に、「線形回帰」「非線形回帰」「ロジスティック回帰」「主成分分析」「k近傍法」「k-平均法」「サポートベクターマシーン」などがある。以下、いわゆるディープラーニング以外の手法について記載。
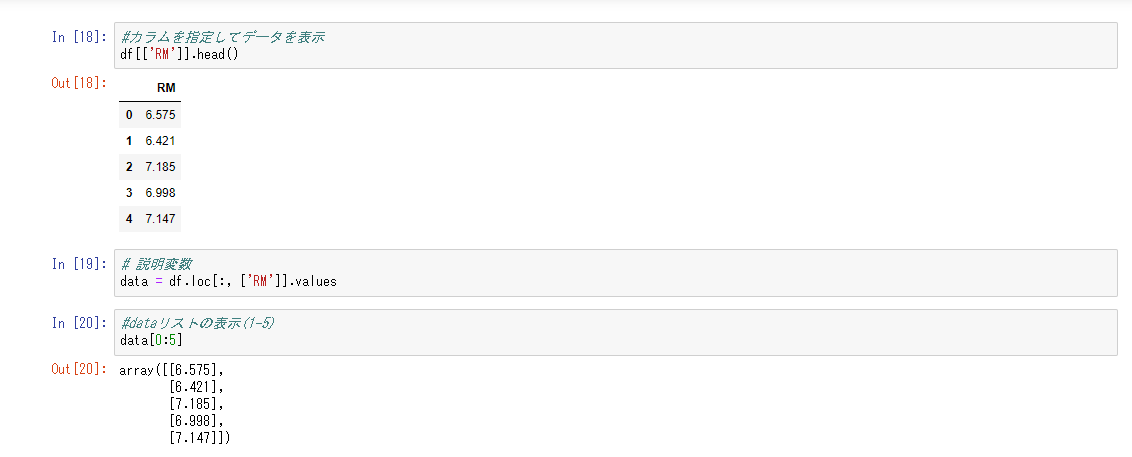
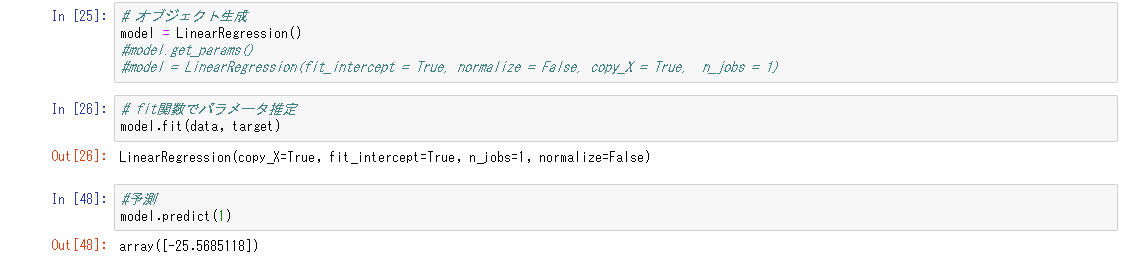
線形回帰モデル
回帰分析とは、ある変数x(説明変数)が与えられたとき、それと相関関係のあるy(目的変数)の値を説明・予測すること。線形回帰(linear regression)とは、統計学における回帰分析の一種。線形回帰は非線形回帰と対比される。線形回帰では、線形関数(1次関数)を仮定しているが、非線形関数を仮定したものは、非線形回帰となる。
https://ja.wikipedia.org/wiki/%E7%B7%9A%E5%BD%A2%E5%9B%9E%E5%B8%B0
http://www.randpy.tokyo/entry/2017/06/16/153435
線形回帰にはさらに、単回帰分析のほかに重回帰分析とがある。単回帰分析が1つの目的変数を1つの説明変数で予測したのに対し、重回帰分析は1つの目的変数を複数の説明変数で予測しようとするもの。身長から体重を予測するのが単回帰分析、身長と腹囲と胸囲から体重を予測するのが重回帰分析。
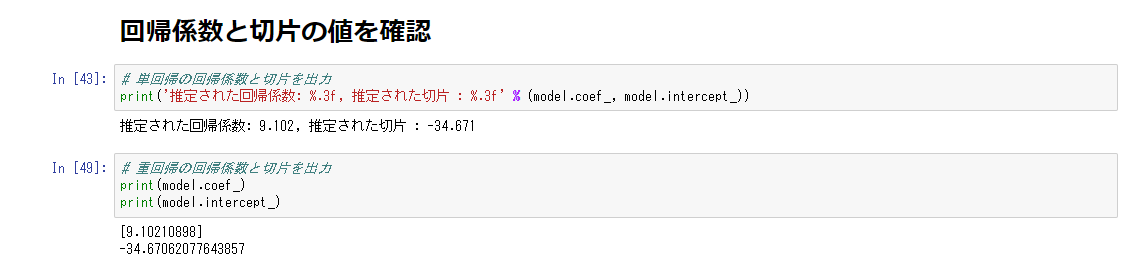
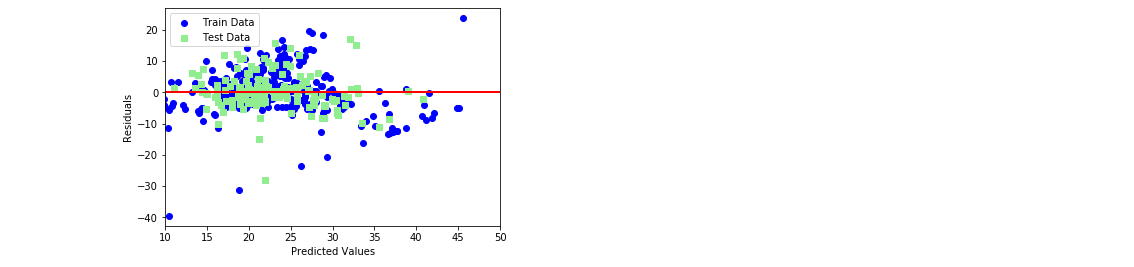
相関関係が直線で表される一次関数に近似できると予想する場合、線形回帰モデルを選択する。ここで直線を引く場合の、「傾き(重み、パラメータ)をどのように決めるのか」が肝要になる。線形回帰モデルでは、**最小二乗法(OLS:Ordinary Least Squares)**を用いる。
説明変数と目的変数との相関をある一次関数で表したとき、データは直線の真上には乗らない。上下へのばらつきが生じる。直線とデータとの誤差(差異)を残差と呼び、各店における残差の和が最小になるようにパラメータを決定する手法が最小二乗法である。生じた残差をできるだけ小さくなるように直線を引くためにパラメータを調節する計算である。
i番目の説明変数を入力して得られる目的変数と、i+1番目のデータを入力して得られる目的変数の差は、+になることもあるし、-になることもある。よって、2乗する。ここで得られたものの総和を取る。直線の傾きにあたるaと、切片にあたるbがともに2乗された関数が得られるので、これの最小となる値を得るため、微分を行う。変数が複数あるため偏微分を用いる。最小の値となるということは傾きである微分値が0となる。方程式を解いた形は、説明変数Xと,目的変数Yの標本共分散をXの標本分散で割った形になる。この場合、上記の最小二乗法が使うためには、誤差項に正規分布を仮定する必要がある。
データの分割
機械学習によって得られたモデルがどのくらいの精度を出せるのか。学習のためにもデータが必要になり、検証のためにもデータが必要となる。よってデータの分割が必要になる。しかしこの分割によって、どの部分を使用するかでモデルも、検証も異なったアウトプットになる。この誤差を少なくする方法としてクロスバリデーション(交差検証)という手法がある。
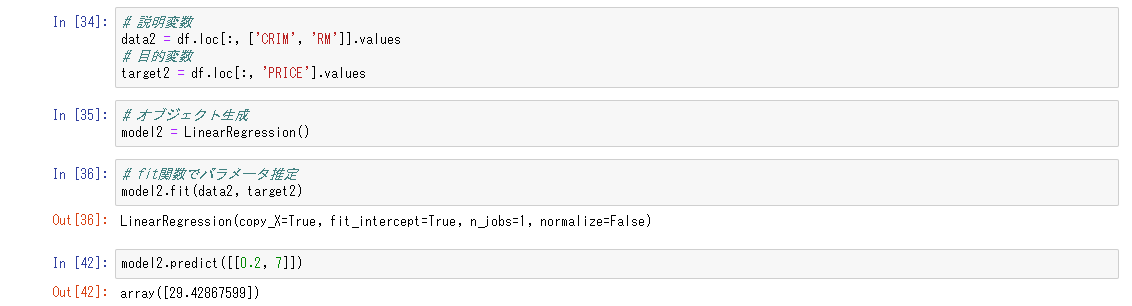
重回帰分析
複数の説明変数を用いて、目的変数を得る回帰式を得る方法。
ex)身長(x1)と、胸囲(x2)から体重(y)を予測する
https://bellcurve.jp/statistics/course/9702.html
複数の説明変数を使用する場合、回帰直線は2次元空間で視覚化できない。ただし、この回帰直線は、単一の説明変数の線形回帰を表す方程式を拡張し、各説明変数に対応するパラメータを追加することによって計算できる。
http://otndnld.oracle.co.jp/document/products/oracle11g/111/doc_dvd/datamine.111/E05704-02/regress.htm
非線形回帰モデル
説明変数xと目的変数yとの関係は、直線では近似できないことがある。この場合、非線形回帰の手法を使用する。
線形でないということは、非線形回帰式がとりうる形式は無限。よって事前に期待関数を指定する必要がある。どの関数を選択するかは、予備知識に基づいて決定する。起こり得る非線形形状としては、凹、凸、指数的な増加または減少、シグモイド(S)、および漸近曲線などがある。さまざまな関数形式を指定できるという柔軟性は非常に強力であるが、データに最適適合する関数形式を決定するために相当な労力が必要になる。このため、追加の調査や対象分野に関する知識、試行錯誤による分析が必要になることが多々ある。また、非線形式の場合、各予測変数が応答に及ぼす影響を判断するということは、線形式の場合ほど直観的ではない。
「多項式関数」「ガウス式基底関数」「スプライン関数/Bスプライン関数」といった関数を基底関数として、既知の非線形関数として用い、パラメータベクトルの線形結合を使用する。
線形結合とは、例えば基底ベクトルを定数倍して足し合わせる計算のことを言う。基底ベクトルは、平面空間であれば(1,0)と(0,1)という線形独立にあるベクトルを定数倍することであらゆる点を表すことができるベクトルのことを言う。
https://qiita.com/nognog/items/f6b6e64792ae1f8ac20c
パラメータの算出には線形回帰で用いた最小二乗法や、最尤法を用いる。
最尤法
統計的推定の際、実際に得られた標本があるとき、それが得られる確率が最大になるような母数の値をその推定値とする手法。
https://kotobank.jp/word/%E6%9C%80%E5%B0%A4%E6%B3%95-68290
ロジスティック回帰モデル
ロジスティック回帰とは、「ある入力が、Aにあたるのか、Bにあたるのか」、という分類問題を解くために使用される手法。
http://tkengo.github.io/blog/2016/06/04/yaruo-machine-learning5/
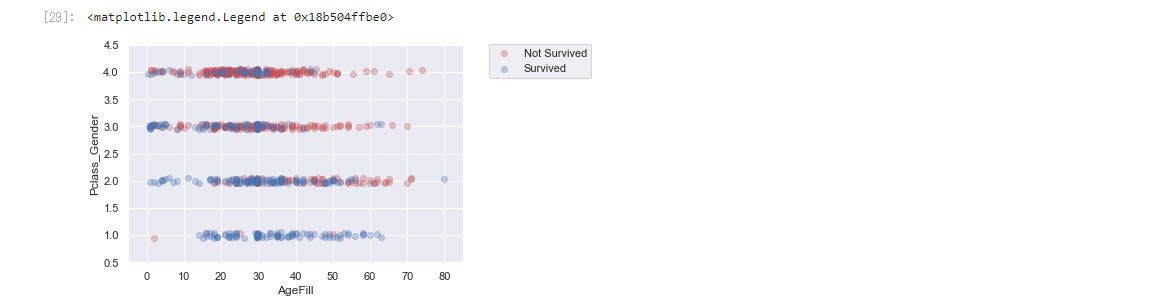
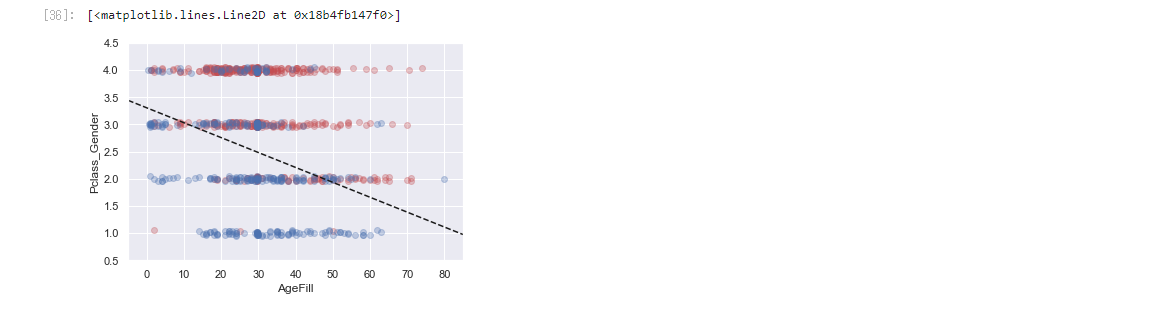
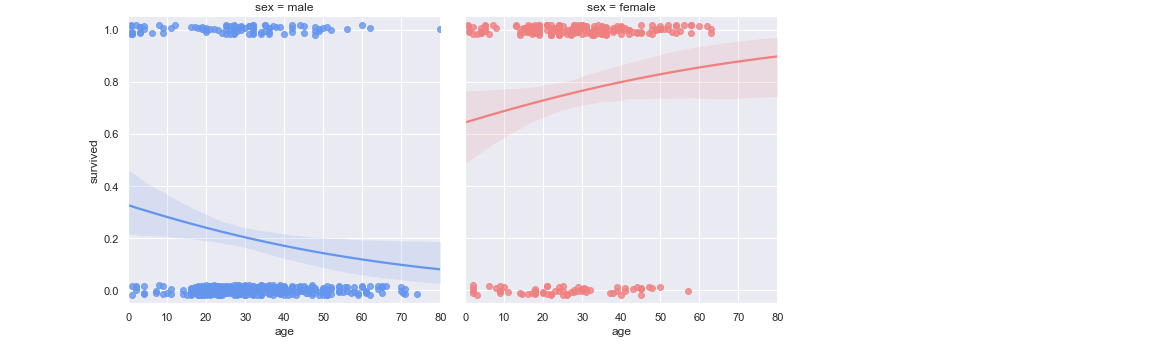
ex)タイタニック号のある乗船客(性別、年齢、乗船した船室の等級)が、生存したのか、命を落としたのか
ロジスティック回帰は分類を確率として考える。先の例でいえば、「死亡する確率60%、生存する確率40%」。
重みの更新式を簡潔に記載するために、生存を「1」、死亡を「0」のように置く。
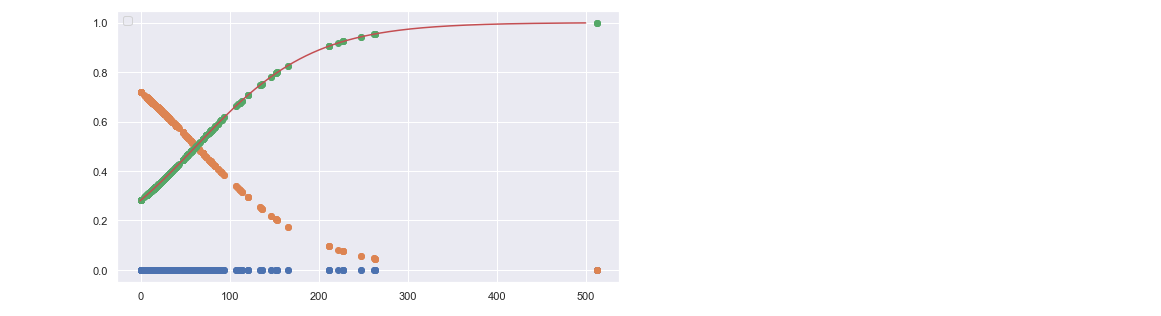
パラメータの算出には、シグモイド関数を用いる。
f(x) = \frac{1}{1+e^{-ax}} \ \ (a>0)
シグモイド関数は、生物の神経細胞が持つ性質をモデル化したものとして用いられる。
ex)ニューロンの発火
シグモイド関数は、微分が自分自身の関数(シグモイド関数)を使って簡単に表現できる。よって、ある値を閾値として、微分値が「0」に近くなるか、「1」に近くなるかを表現しやすい。
次に、モデルを導出するにあたり必要となるパラメータ決定の問題を考える。回帰分析の際には、誤差を最小とするような、各データの並びを近似するような線を引くために、最小二乗法を用いた。しかし、分類問題を目的とするロジスティック回帰では、データを分類する問題を考えたいために、回帰分析とは違うアプローチを考える必要がある。つまりそれは、「0」か「1」になる確率を最大化するパラメータを見つける手法である。
「0」か「1」かという問題は、コインを投げたときに「表」が出るか、「裏」が出るかというベルヌーイ分布を考える問題としてとらえることができる。
〇目的変数yが1のときには、xが1である確率を最大にしたい
〇目的変数yが0のときには、xが0である確率を最大にしたい
学習用データについて、上記条件の直積を取る、つまり同時確率を求め、これを最大とするパラメータを求める。確率が、学習用データに最大限フィットする、尤もらしい値を取る関数、これを尤度関数という。
https://tkengo.github.io/blog/2016/06/16/yaruo-machine-learning6/
尤度関数をを最大とするパラメータを探すため、勾配降下法を用いる。また、同時確率の計算は1より小さい数の直積となることからコンピュータにとって大変な計算となるため、積を和に変換するため対数を用いる。これが対数尤度関数を用いる理由である。勾配降下法より、簡便な計算手法として、確率的勾配降下法がある。
主成分分析
多変量解析とは、統計学において、複数の独立変数(説明変数)からなる多変量データを統計的に扱う手法である。主成分分析、因子分析、クラスター分析などがある。一般に、多変量解析を行うためには計算負荷が高く手計算ではきわめて困難だが、コンピュータの発展により、容易に実行できるようになった。
多変量解析の手法は、目的変数がある場合とない場合の二つに分けられる。目的変数のない場合の手法は、説明変数が数量データの場合とカテゴリーデータの場合の二つに分けられる。説明変数が数量データの場合の手法は、主成分分析と因子分析がある。どちらの手法も、数多くの変数から新しい概念の変数を作る。新しく作られた概念の変数を潜在変数といいう。これに対し、元の変数を観測変数という。
本項は、目的変数がなく、説明変数が数量データである場合の手法である、主成分分析(principal component analysis; PCA)について述べる。
https://logics-of-blue.com/principal-components-analysis/
https://qiita.com/NoriakiOshita/items/460247bb57c22973a5f0
http://bdm.change-jp.com/?p=2761
https://istat.co.jp/ta_commentary/analysis
https://ja.wikipedia.org/wiki/%E5%A4%9A%E5%A4%89%E9%87%8F%E8%A7%A3%E6%9E%90
企業規模や、学力など、単一の説明変数だけでは順位付けや分析が困難なものを考える。複数の企業を企業規模で順位付けしたい場合、従業員数、資産、売り上げ、ROEなど複数の説明変数が存在し、単一の説明変数だけでは企業規模を順位付けすることはできない。また、堅実経営の企業や、ブランド価値が高い企業など、企業には単一の説明変数だけを見ていてはわからない評価基準が存在することが予想される。また学力についても、英語・数学・理科・社会・国語など単一の説明変数だけでは、科目ごとの順位・得意不得意は容易に算出できても、個人の総合的な順位付けや集団で見た場合の傾向をとらえることができない。単純な5教科の合計点では、科目ごとに平均点が異なることから、単純な合算値では総合的かつ多角的な学力評価とはなりえない。
「5」教科からなる観測変数を、「文系能力」「理系能力」のような2つの潜在変数に集約するような作業、つまり次元数を落としながら、もとの情報の損失を抑える分析手法である。傾向をとらえるような潜在変数を導出する次元圧縮を行うのが因子分析であり、総合力をとらえるような潜在変数を導出する次元圧縮を行うのが主成分分析である。
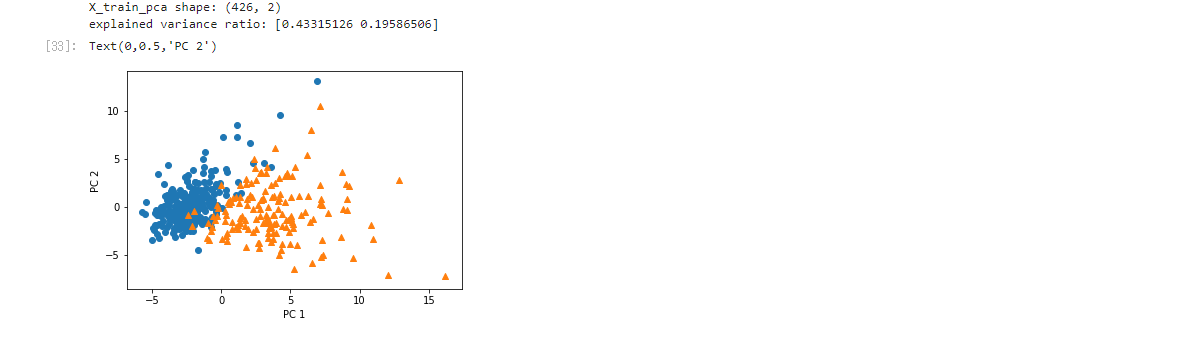
多変量・多次元のビッグデータをそのままマトリクス的に眺めても、比較や傾向把握は困難である。主成分分析では、全体をわかりやすく見通しの良い1~3程度の次元に要約し、かつデータの持つ情報をできる限り損なわずにデータ全体の見通しを可視化することを目的とする。
複数の変数から最初に生み出した潜在変数を「第一主成分」、2番目に生み出した潜在変数を「第2主成分」と呼ぶ。「第1主成分」だけでなく「第2主成分」、「第3主成分」などを組み合わせて散布図を作成し、分析結果を解釈するのが一般的。
主成分を見つけるためには,分散が最大になるような軸を探す。分散共分散行列の固有ベクトルについて解き、最大固有値に対応する固有ベクトルで線形変換された特長量を第一主成分と呼ぶ。k番目の固有値に対応する固有ベクトルで変換された特長量を第k主成分と呼ぶ。分散に対応する最大固有値に対応する固有ベクトルを選ぶことによって、データを圧縮していると考えられる。
次に寄与率について考える。第1主成分の寄与率は第1主成分がデータ全体のデータの散らばり具合をどれくらいカバーしているかを表す。第2主成分以降も同様。累積寄与率とは、第1主成分から第m主成分までの寄与率の和である。
第1主成分から第k主成分での圧縮がデータの散らばり具合をどの程度カバーしているかの説明する割合である(1に近ければデータの散らばり具合を説明できている割合が高いことになる)。
k近傍法
https://ja.wikipedia.org/wiki/K%E8%BF%91%E5%82%8D%E6%B3%95
https://qiita.com/yshi12/items/26771139672d40a0be32
https://qiita.com/NoriakiOshita/items/698056cb74819624461f
k近傍法(k-nearest neighbor :k-NN)は分類問題を解くための機械学習のアルゴリズムの一つであり、最も簡単な機械学習のアルゴリズムの一つとされている。教師あり学習に属する。後述するk平均法はクラスタリングのアルゴリズムの一種であり、教師なし学習に属する。
k近傍法では、学習データをベクトル空間上にプロットしておき、未知のデータが得られたら、そこから距離が近い順に任意のK個を取得し、多数決でデータが属するクラスを推定する。分類したいデータを中心とした円を描き、ラベル付き学習済みデータをk個含んだとき、その中でラベルの多いものに、未知のデータの分類が決定される。
Kの値を変化させることで、結果も異なってくる。kの選び方には諸説あり、より多く用いられてるのはkの総数の平方根を取るものである。
k-平均法
https://qiita.com/NoriakiOshita/items/698056cb74819624461f
https://www.albert2005.co.jp/knowledge/data_mining/cluster/non-hierarchical_clustering
k平均法はクラスタリングのアルゴリズムの一種である。教師なし学習に属する。k近傍法は教師あり学習であったので、データラベルが既知であった。しかしk平均法においてはそのようなデータを前提としない学習である。
k平均法のアプローチではまず最初に乱数でクラスタ中心を割り当てる。クラスタ数の決め方も乱数で決めたり,試行錯誤による。標本数にもよるが,重心を求め、標本を近いクラスタ中心に割り当てるという作業を何回が繰り返す。k平均法は、各クラスタの散らばり具合を最小にするようなクラスタラベルを割り当てる。
k平均法は、非階層クラスター分析の代表的手法である。非階層クラスター分析とは、異なる性質のものが混ざり合った集団から、互いに似た性質を持つものを集め、クラスターを作る方法の1つである。階層クラスター分析と異なり、階層的な構造を持たず、あらかじめいくつのクラスターに分けるかを決め、決めた数の塊(排他的部分集合)にサンプルを分割する方法といえる。階層クラスター分析と違い、サンプル数が大きいビッグデータを分析するときに適している。ただし、あらかじめいくつのクラスターに分けるかは、分析者が決める必要があり、最適クラスター数を自動的には計算する方法は確立されていない。
サポートベクターマシーン
https://ja.wikipedia.org/wiki/%E3%82%B5%E3%83%9D%E3%83%BC%E3%83%88%E3%83%99%E3%82%AF%E3%82%BF%E3%83%BC%E3%83%9E%E3%82%B7%E3%83%B3
https://logics-of-blue.com/svm-concept/
http://proger.blog10.fc2.com/blog-entry-34.html
http://www.sist.ac.jp/~kanakubo/research/neuro/supportvectormachine.html
サポートベクターマシン(support vector machine, SVM)は、教師あり学習を用いるパターン認識モデルの一つである。分類や回帰へ適用できる。サポートベクターマシンは、現在知られている手法の中でも認識性能が優れた学習モデルの一つである。サポートベクターマシンが優れた認識性能を発揮することができる理由は、未学習データに対して高い識別性能を得るための工夫があるためである。
「部分的な最適解に系が収束し、本当の最適解にたどり着かない」という局所解問題(ローカルミニマム問題:local minumum problem)や、「特定の入力と出力の組み合わせ(学習データ)に対して系が収束しすぎたために、その他の入力(非学習データ)に対する汎用性がなくなってしまう状態」過学習への対処があるという特徴も有す。
SVMは厳密にはニューラルネットワークではないが、中間層から出力層への結合係数に該当するものを計算し、ニューラルネットワークと関連付けられることもある。
SVMはデータを2つのグループに分類する問題に優れている。
予測には過去のデータを使用する。しかし、外れ値のような余計なデータまで使ってしまうと、予測精度が下がる。そこで「本当に予測に必要となる一部のデータ」だけを使用する。「本当に予測に必要となる一部のデータ」のことをサポートベクトルと呼び、サポートベクトルを用いた機械学習法がサポートベクトルマシン(Sapport vector machine:SVM)である。
名前の由来である「サポートベクトル」とは、先にあげた「予測に必要となる一部のデータ」である。「予測に必要となる一部のデータ」を定めるのに「マージン最大化」と呼ばれる考え方を使用する。マージンとは、「判別する境界とデータとの距離」を指す。これが大きければ、「ほんの少しデータが変わっただけで誤判定してしまう」というミスをなくすことができる。なお、境界線と最も近くにあるデータを「サポートベクトル」と呼びます。
境界の近くにあるデータは、言い換えると「AかBか微妙」な位置にあるデータだとみなすことができる。「どちらか分けにくいデータ」が多い場合、予測が困難になるので、境界とデータとの距離、すなわちマージンを大きくするようにして誤判別を防ぐ。
逆にいれば、誤判別を防ぐには「境界の近くにあるデータ」だけあれば十分である。明らかに、分類可能なデータをすべて計算する必要はなく、境界の近くにあるデータ、すなわちサポートベクトルのみを用いて分類を行う。サポートベクトル以外のデータの値が多少変化したとしても、分類のための境界線の位置は変化しない。
AかBか確実に分類できることを前提としたマージンを「ハードマージン」と呼ぶ。「手持ちのデータ」に対して無理に適合性を高めてしまい、「まだ手に入れていないデータ」への予測精度が下がってしまう問題を「過学習」と呼ぶ。過学習をせずに予測ができることを「汎化性」と呼び、この汎化性能を高めるために、あえて誤分類を許すように工夫する。このような誤判別を許すことを前提としたマージンのことを「ソフトマージン」と呼びます。
ソフトマージンは以下の2つを満たすように調整する。
・境界線とデータとはなるべく離れていたほうがいい
・誤判別はなるべく少ないほうがいい
そこで、以下のように、マージンを最小にする目的関数を計算する。
min{1/マージン(サポートベクトルと境界線の距離)+C×誤判別数}
※Cは、「誤判別をどこまで許容するか」を現すパラメタ
パラメタCが∞に大きかった場合は「誤判別は1回も許さない」という強い制約となり、実質ハードマージンと変わらなくなる。パラメタCが小さければ、多少誤判別があっても上記の式の合計は大きくならないので誤判別を許しやすくなる。
パラメタCは人間があらかじめ決めてやる必要がある。このように「あらかじめ与えられていることが前提のパラメタ」のことを「ハイパーパラメタ」などと呼ぶ。パラメタCは暫定的に決めるしかないが、グリッドサーチなどを使って「最も予測精度が高くなるようにパラメタをチューニングする」技術もある。なお、ソフトマージンの場合は、誤判別されたデータに関しても「識別境界線を決める要素」すなわちサポートベクトルだとみなす。