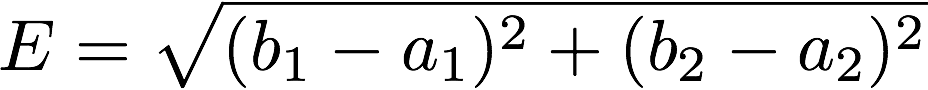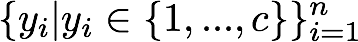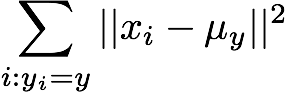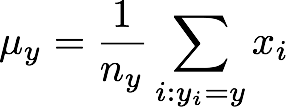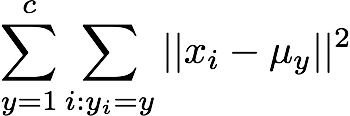この記事の内容
・k近傍法とk平均法の説明
・k近傍法とk平均法の違いについて軽く説明
・k近傍法の具体的な手法の説明
・k平均法の具体的な手法の説明
・あとがき
という流れになっています.
k近傍法とk平均法とは
k近傍法(k-nearest neighbor :k-NN)とk平均法(k-means clustering)というのは名前も似てて最初は同じものだと誤解する人もいるでしょう.現に私もそう思っていました.実際には似たようなアルゴリズムの考え方ですが,若干その考え方が違います.
まずk近傍法は機械学習のアルゴリズムの一つです.最も簡単な機械学習のアルゴリズムの一つとされており,遅延学習に分類されます.
k平均法はクラスタリングのアルゴリズムの一種です.クラスリングと機械学習の用語の違いの定義を確認しましょう.
k近傍法とk平均法の違いとは.
二つとも広義的には機械学習のアルゴリズムとみなすことができますが,明確に違いを分けることによって二つの異なるアルゴリズムの違いについて理解することができます.
k近傍法とは教師あり(付き)学習の分類問題とみなすことができます.そしてk平均法はクラスタリングという手法であり,教師なし学習の分類問題とみなします.
この可愛らしい絵は私が数十分かけて描いたものですが,k近傍法は教師あり学習であるので,イメージ的には答えが分かってる問題を教師が教えながら学習していきます.(実際には学習前に教師ラベルが既知です.)k平均法を代表とするクラスタリングは教師なし学習なので,ウェブのデータなど特に人がどういうデータであると定義していないようなデータであり入手も簡単ですが,教師あり学習よりも学習が難しかったり複雑である場合が多いです.
k近傍法の数学的理解
k近傍法での距離はユークリッド距離を使うことが一般的です.理由は詳しくは知りませんが,慣習的にそうということとマンハッタン距離よりも計算手間が少なく,また直感的に理解がしやすいということが挙げられると思います.
この場合のユークリッド距離E(画像の青い線分の長さ)は次のように表されます.
これは三平方の定理を使えばすぐに求めることができるので問題ないと思います.
具体的な問題
メロンが野菜であるか,果物であるか,脂質であるかを分類する問題を考えます.メロン以外に複数の食材があり,メロン以外の食材の甘さと歯ごたえ,タイプが分かっているとします.(教師あり学習のため当然の前提です)甘さと歯ごたえから距離を求めることができます.
次に具体的な食材の甘さと歯ごたえの数値を表に示す.
| 食材 | 甘さ | 歯ごたえ | タイプ | メロンとの距離 |
|---|---|---|---|---|
| メロン | 9 | 6 | -------- | -------- |
| レンコン | 2 | 6 | 野菜 | √((9-2)^2+(6-6)^2) = 7.00 |
| キュウリ | 1 | 9 | 野菜 | √((9-1)^2+(6-9)^2) = 8.54 |
| 豚肉 | 1 | 2 | 脂質 | √((9-1)^2+(6-2)^2) = 8.94 |
| お米 | 2 | 1 | 脂質 | √((9-2)^2+(6-1)^2) = 8.60 |
| チョコ | 10 | 3 | 脂質 | √((9-10)^2+(6-3)^2) = 3.16 |
| 桃 | 8 | 5 | 果物 | √((9-7)^2+(6-2)^2) = 4.47 |
| オレンジ | 5 | 3 | 果物 | √((9-5)^2+(6-3)^2) = 5.0 |
k近傍法において$k$とはインスタンスの数を意味します.
$$ \{ k \in \mathbb{N}|k \geq 1 \} (kは自然数に属し、kは1以上のものを一つ固定する。)$$
ここでのインスタンスとはメロン以外の食材を表します.kが1(1-NNによる分類)の場合は最も近いインスタンス(食材)が選ばれます.
簡単な数理的説明
この時インスタンスを $\{x_k | k = 1,2,3,\cdots , n\}$とすると
これはメロンを中心点として2次元球の円を広げて一つのインスタンスすなわち$x_1$が入る時k=1と言っているともいえます。
$x_n$は一番遠いい食材を表す。
さて先ほどの場合は表から3.16のチョコが選ばれ脂質と分類されてしまいます.チョコはノイズと考えるのが妥当でしょう.この場合,kが小さすぎるため,ノイズによって過少適合になってしまいました.ではkの値を3にするとどうなるでしょう.
答えは,果物である,桃とオレンジが加わるので頻度で算出すれば果物と分類してくれます.下の図を見てもらうとわかりやすいかと思います。
kの選び方には諸説ありますが,より多く用いられてるのはkの総数の平方根です.
今回の問題だとkの総数は8です.
√8は約2.82なので3という数字は妥当ですね.
ここでk近傍法のメリットとデメリットについて表に示します.
| メリット | デメリット |
|---|---|
| 単純で効果的. | モデルを作らないので,特徴量がクラスとどのような関連があるかの理解が難しい. |
| 土台となるデータの分布について前提条件を設けない. | 適切なkを選択しなければならない. |
| 高速に訓練できる | 分類フェーズが遅い. |
| 名義特徴量と欠損値のために別の処理が必要になる. |
k平均法とは
k平均法(k-means clustering)とはクラスタリングの最も簡単な手法の一つであり,教師なし学習です.
k近傍法は教師あり学習だったのでデータが果物か野菜かなどのラベルが既知でしたがk平均法においてはそのようなデータを前提としない学習です.
一例として適当に集めたウェブのデータなどが該当します.
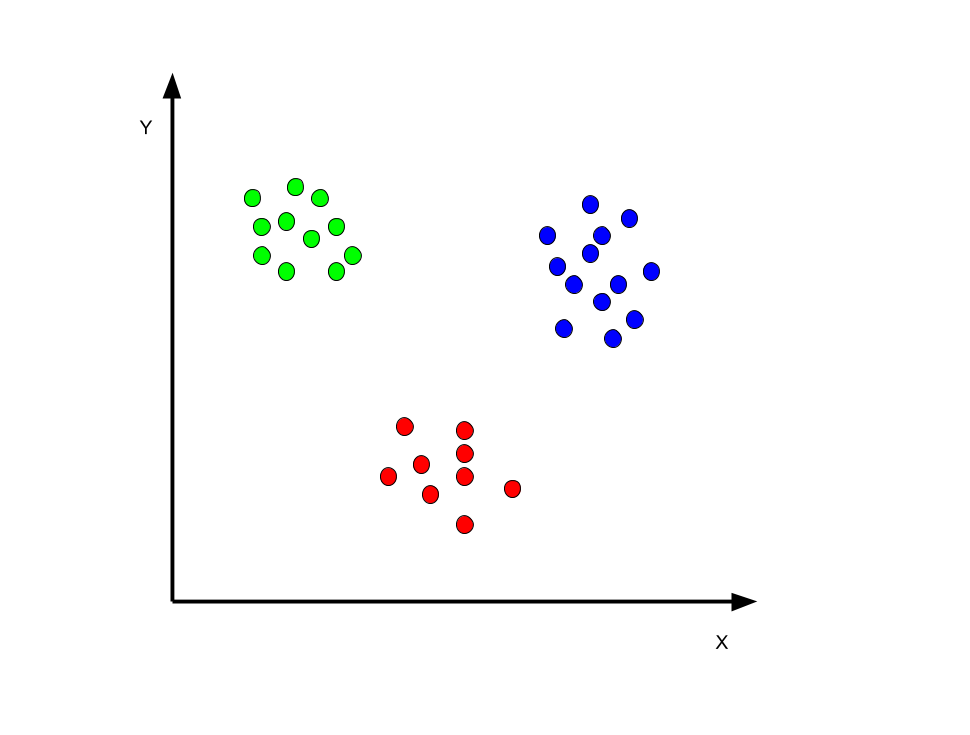
まずはイラストで理解しましょう.以下の図のように何の変哲も無い点の集合があるとします.
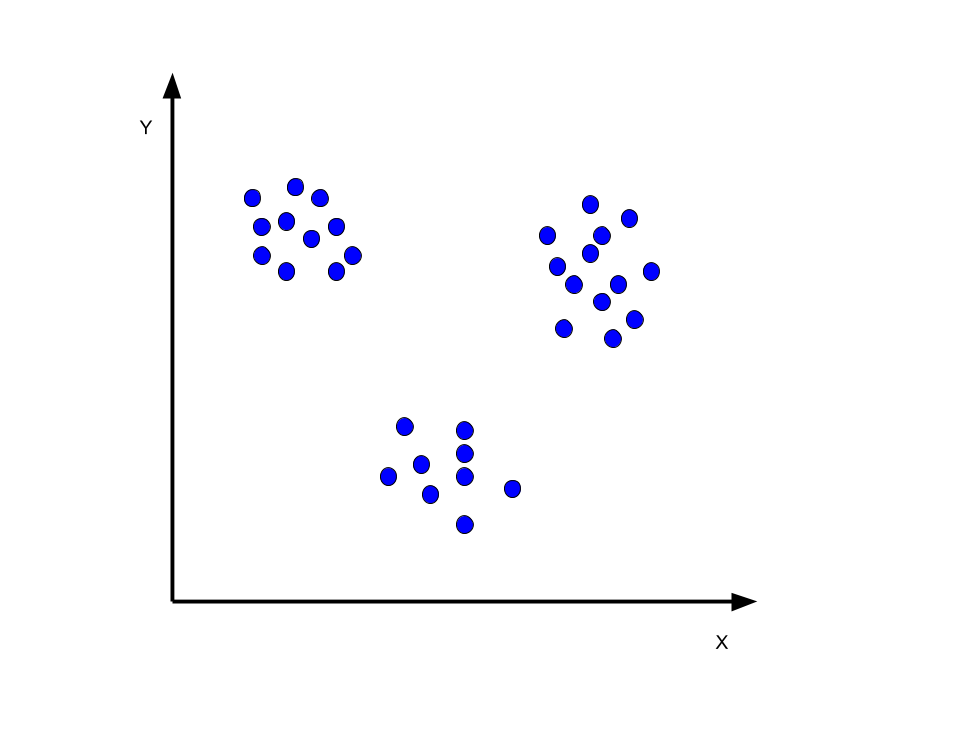
あなたはこの青い点が何を意味しているのを知りません.あなたには教師はいません.独学でデータを分類しなくてはいけません.
青い点を見ると何となく三つの塊に分類できそうです.(現実問題としてこのようなデータは考えにくいです笑)
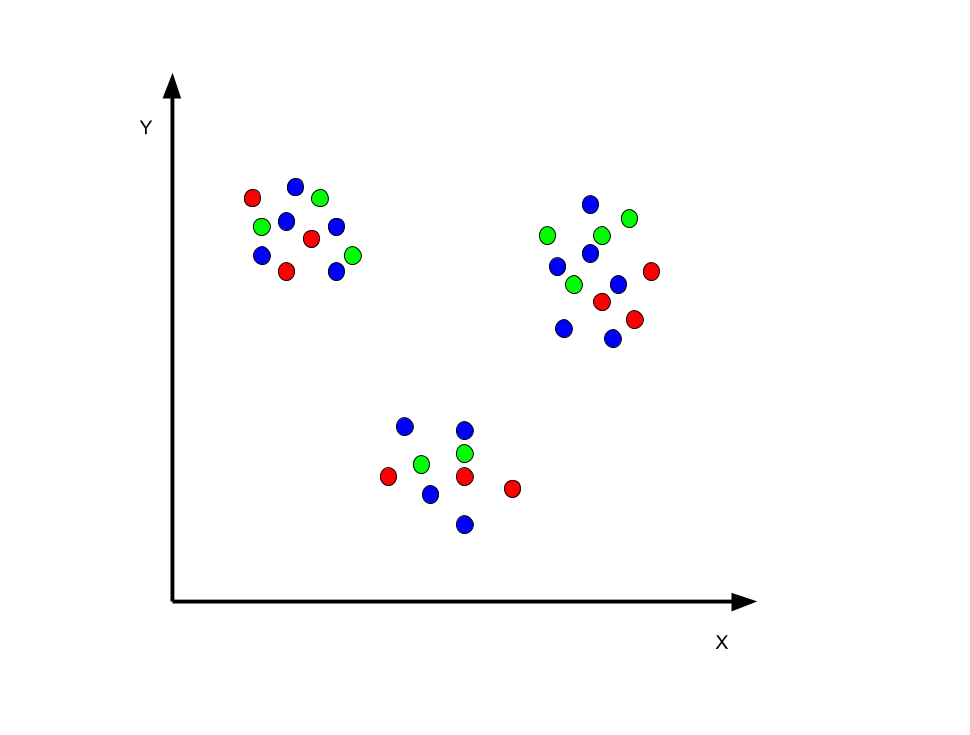
k平均法のアプローチではまず最初に乱数でクラスタ中心を割り当てます.
現実ではクラスタ数の決め方も乱数で決めたり,試行錯誤で決めたりするかと思いますが,今回はクラスタ数を3としましょう.
すると上のように全くデタラメなクラスタに分類されます.乱数で決めるのでこのプロセスは仕方ないのです.
ここでは重心を求めています.
重心を求めたら標本xiを自分のクラスタ中心に近いクラスタに割り当てます.
標本Xの個数にもよりますが,重心を求める,標本xiを近いクラスタ中心に割り当てるというこの作業を何回が繰り返すと,上の図のようになります.
[追記]
実際の動作とコードがあった方が理解が進むと思うので作ってみました.
重心の数を9にして実際にGIF動画にして動作を描画したものが以下になります.
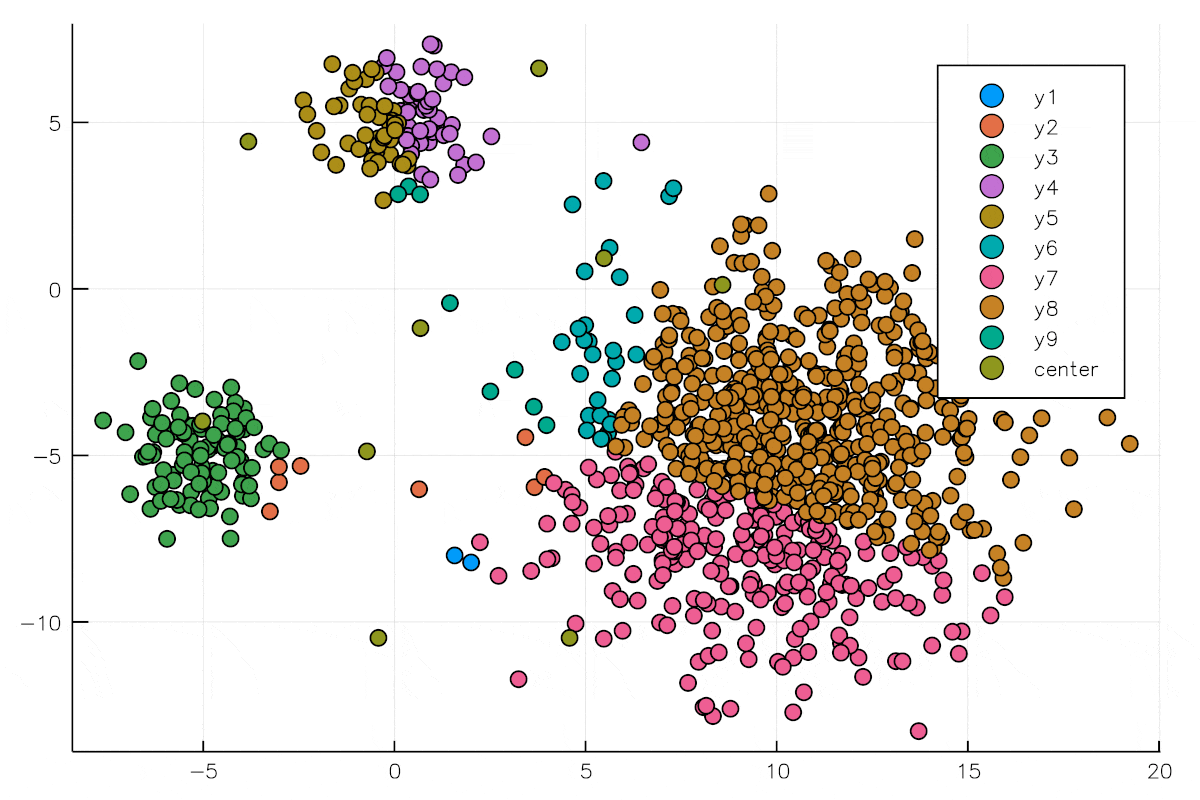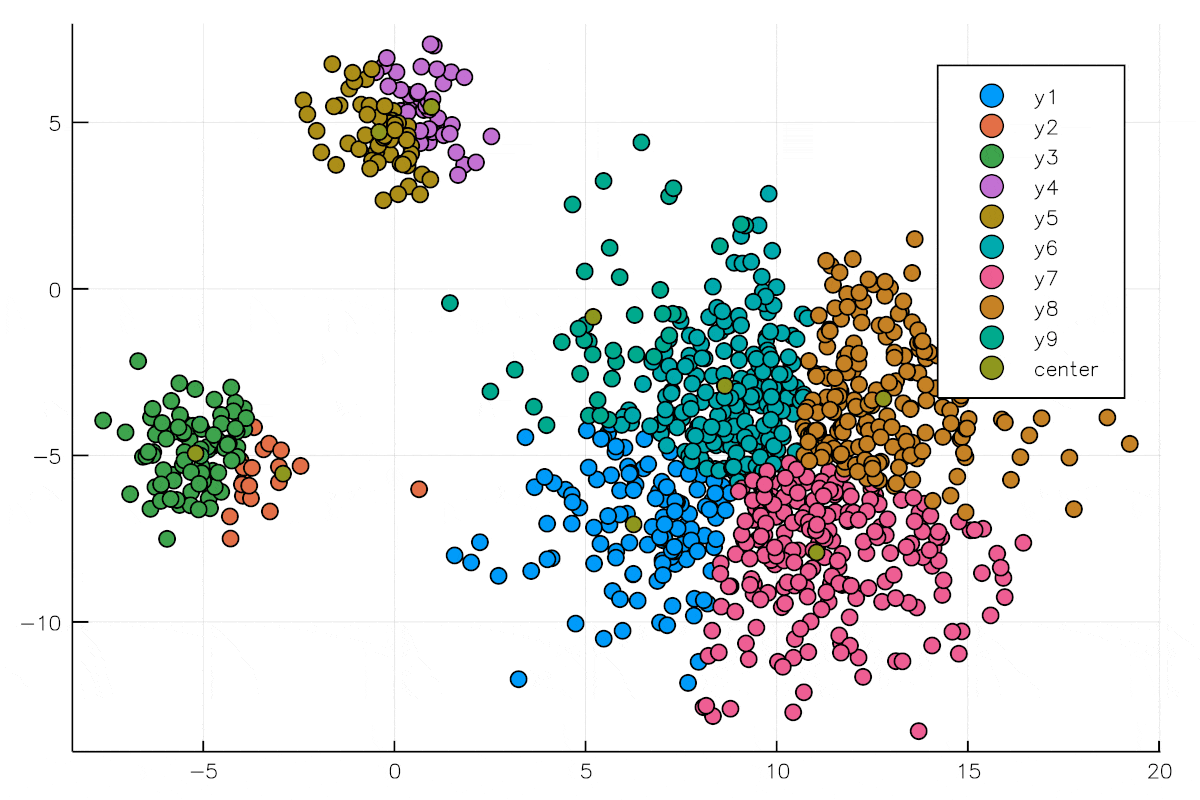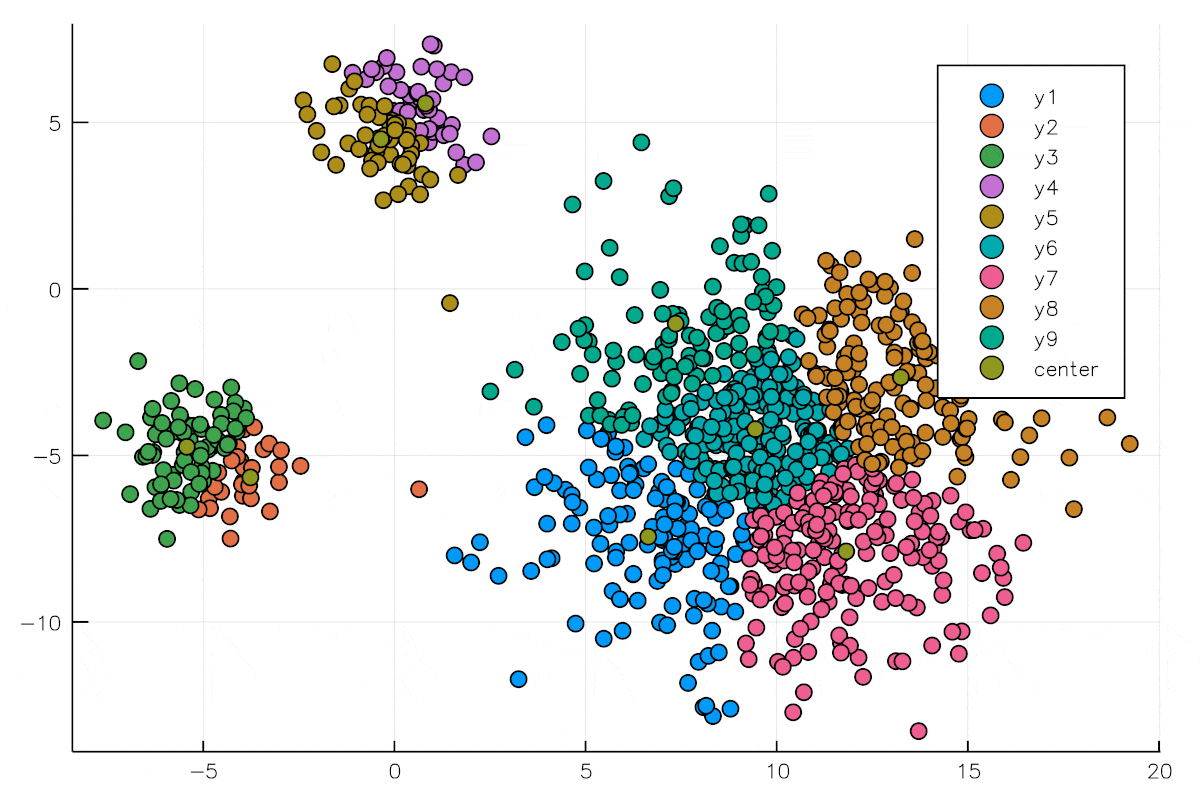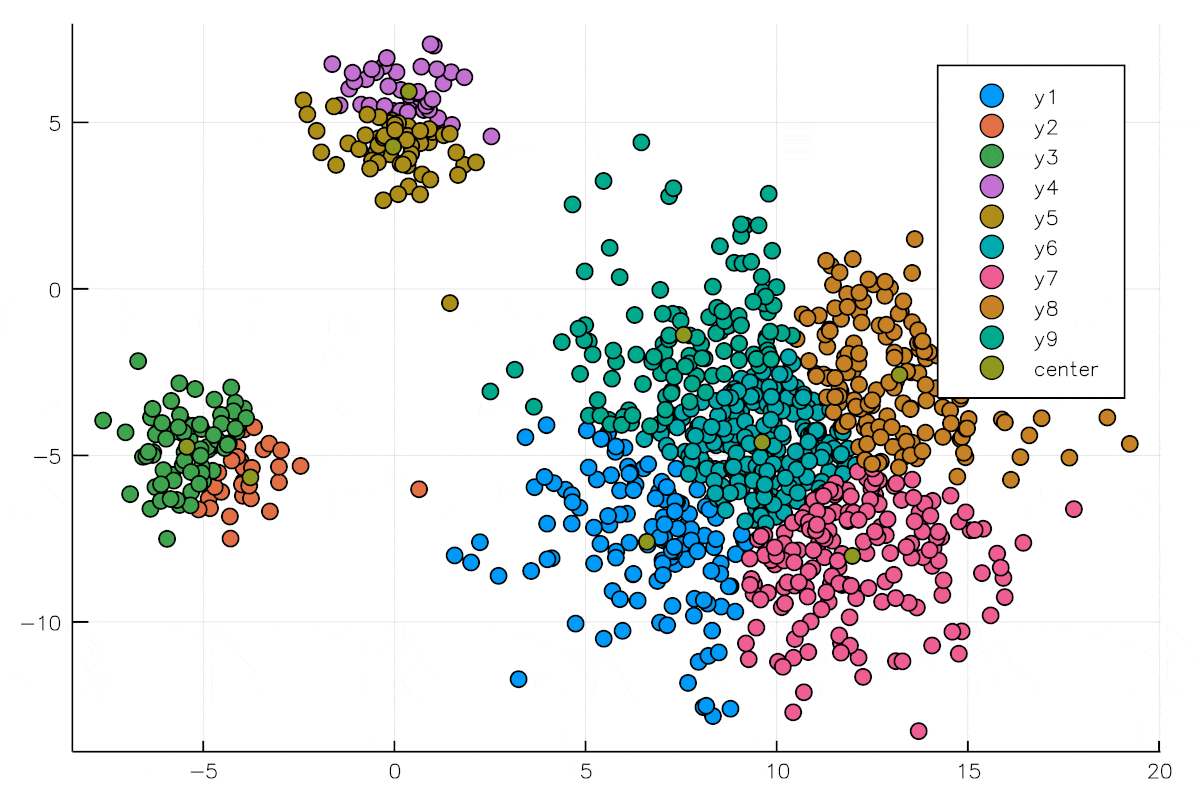
コードは以下に置いております.
https://nbviewer.jupyter.org/github/Ooshita/ml_page/blob/master/julia/kmeans実装2.ipynb
k平均法を数式で理解
k平均法は,各クラスタの散らばり具合を最小にするようなクラスタラベル
を標本
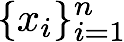
に割り当てます.この時に上で説明したように通常は乱数によって標本を各クラスタ中心に割り当てます.cはクラスタを意味しています.クラスタを3に設定した場合,クラスタラベルyiは1から3までのクラスタの要素ということになります.具体的には,
上の数式によって,クラスタyの散らばり具合を測ります.i:yi=yの意味はyi=yであるiに関する和を表しています.
このμyはクラスタyの中心を表しています.nyはクラスタyに属する標本数です.
この規準を全てのクラスター1からcに関して足し合わせたものを最小にするようにクラスタラベル
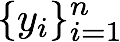
を決定します.
k平均法の問題点
k平均法は見てもらって分かる通り,非常に簡素な考え方で構成されており(数学が苦手な人は面を食らったかもしれませんが...ひとつひとつ意味を理解していけばさほど難しくありません.)強力なクラスタリングの手法ですが,線形分離可能なデータしか分けることができません.この問題を解決するにはカーネルトリックと言われる手法やk平均法の問題を改善したEM法を使う必要があります.
あとがき
どうでしょうか,k近傍法とk平均法の違いについて理解していただけたでしょうか?
どちらも名前が似ていますが,以外に並べて手法を説明して見ると結構違うということがわかったと思います.
数式をできるだけ使用している理由としては本当に理解するということは数式を見て分かることだと僕が思っているからです.プログラムもこの記事では一切書いていませんが,その理由はQiitaにも沢山そのような記事があったこと,なので僕は理論的に手法を説明した記事を書いてみたかったからです.
次はまた勉強が進行具合によってまた別の手法に関する記事を書けたらと思います.
何か間違いや質問などあれば遠慮せずコメント欄に書いてくださると嬉しいです.
参考文献
Rによる機械学習
鈴木先生の資料
http://ibis.t.u-tokyo.ac.jp/suzuki/lecture/2015/dataanalysis/L10.pdf