1. Overview
"Sample Adaptive MCMC$^{[1]}$"という新しいMCMCをNIPS2019のProseedingで見つけたので実験してみた。Numpyroには既に実装済み。興味を持たれた方は是非論文を見てください。
MCMC法では提案分布の調整が重要だが、本手法はサンプル値に基づいてパラメトリック提案分布(正規分布等)のパラメータ(平均、共分散行列)を適応的に調整する手法である。また、有効サンプルサイズを稼ぎやすい手法である。
[1] Michael Zhu, Sample Adaptive MCMC (https://papers.nips.cc/paper/9107-sample-adaptive-mcmc)
2. Algorithm
アルゴリズムの概要は、$N$個のサンプル値から平均$μ$と共分散行列$Σ$を計算し、この平均$μ$と共分散行列$Σ$をパラメータとするパラメトリック提案分布から新たなサンプル値$θ_{N+1}$をサンプリングする。これらの$N+1$個のサンプル値から確率的にどれか一つを破棄し、新たに構成された$N$個のサンプル値の平均$μ$と共分散行列$Σ$を計算し…という手順を繰り返し、最終的に得られたサンプル値の和集合が目的分布の近似となる。
アルゴリズムは下記のとおりである。ここで、サンプル対象である$θ$は多次元ベクトルとする。
Input:目的分布$p(θ)$、初期提案分布$q_0(・)$、パラメトリック提案分布$q(・|μ,Σ)$、粒子数$N$、サンプル数$K$、バーンイン数$κ$
Step.1
初期提案分布$q_0(・)$から$N$個のサンプル値$S_0=${$θ_1, θ_2,...θ_N$}を取得する。$k=1$とする。
Step.2
・$S_{k-1}$を$S$に代入し、サンプル値$S$から平均$μ$と共分散行列$Σ$を計算する。
・パラメトリック提案分布$q(・|μ,Σ)$から新たなサンプル値$θ_{N+1}$を取得し、$S$に追加する。
・$S$の$n$番目のサンプル値$θ_n$を除外した$S_{-n}$を$N+1$セット作り、平均$μ_{-n}$と共分散行列$Σ_{-n}$を$N+1$個計算する。
・$λ_n=q(θ_n|μ_{-n},Σ_{-n})/p(θn)$を全ての$n(=1~N+1)$に対して計算し、総和が$1$になるよう規格化する。
・$λ_n$が$z_n=1$となる確率としてカテゴリカル分布から$z_n=1$となる$n$を取得し、$S_k=S_{-n}$とする。
Step.3
繰り返し数がサンプル数$K$に至る迄、__Step.2__を繰り返す。
Output:$S_k(k=κ+1~K)$の要素$θ$の和集合
下図は論文に記載されている$N=3$とした時のイメージ図です。
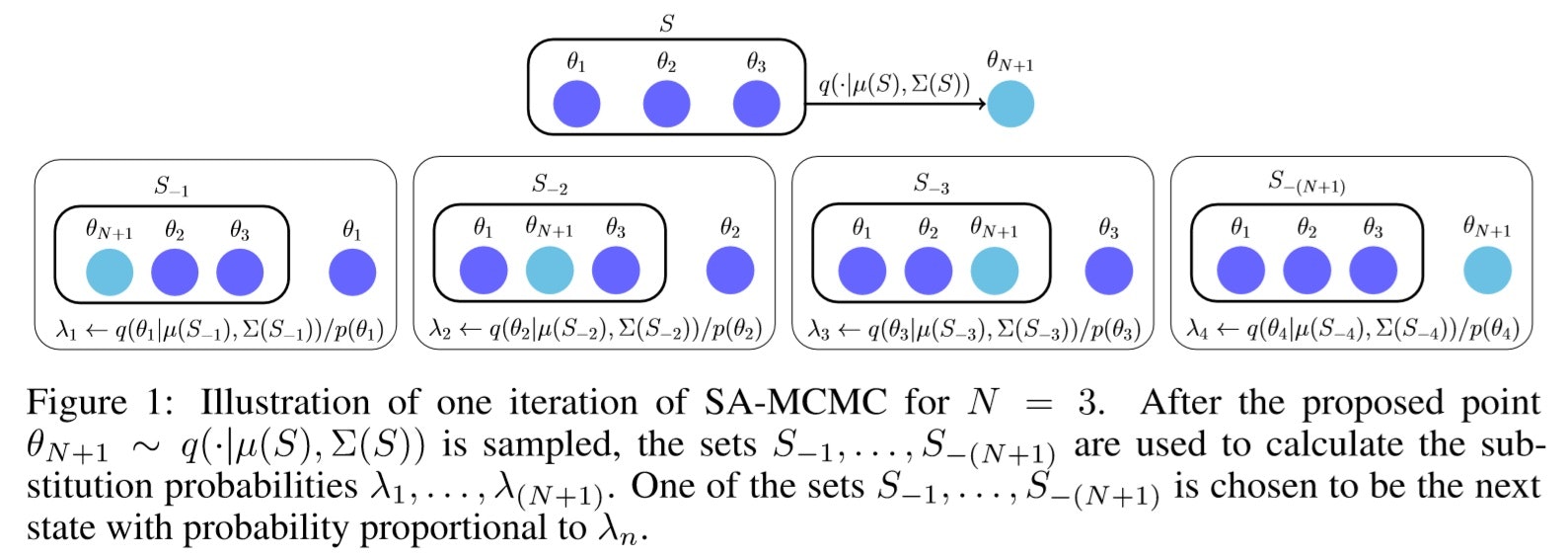
なお、$θ$が多次元の場合、共分散行列を用いると計算負荷が高くなるため、共分散行列の非対角成分を$0$にして近似することで高速化することが可能である。また、パラメトリック提案分布には混合ガウス分布を使用することも可能。
3. Implementation
理解促進のめにPythonで実装してみた。ここでは、線形モデルを想定して計画行列、観測値、測定精度もinputとして与えている。
# SA-MCMC
import numpy as np
from numba import jit
# 規格化していない目的分布pの対数確率密度
@jit("f8(f8[:,:],f8[:],f8[:],f8)", nopython=True)
def target(X, y, w, ram):
mu_w0 = 0.0
ram_w0 =1.0
logp1 = np.sum(-0.5 * ram_w0 * (w - mu_w0) ** 2)# logP(w)+C
logp2 = np.sum(-0.5 * ram * (y - X @ w) ** 2) # logP(y|X, w, ram)+C
logp = logp1 + logp2
return logp
# 規格化していない提案分布qの対数確率密度
@jit("f8(f8[:],f8[:,:],f8[:])", nopython=True)
def proposal(mu, cov, sita):
A = -0.5 * np.linalg.slogdet(cov)[1]
B = -0.5 * (sita - mu).T @ np.linalg.solve(cov, (sita - mu))
return A+B
# 提案分布qからのサンプリング
@jit("f8[:](f8[:],f8[:,:], i8)", nopython=True)
def sampling(mu, cov, w_dim):
L = np.linalg.cholesky(cov)
t = np.random.randn(w_dim)
return L @ t + mu
# 平均値の逐次更新
@jit("f8[:](f8[:], f8[:], f8[:], i8)", nopython=True)
def update_mean(mean, new_s, old_s, N):
mu = mean + 1/N * (new_s - old_s)
return mu
@jit("f8[:,:](f8[:,:],f8[:],f8,i8,i8,i8,f8[:])", nopython=True)
def SA_MCMC(X, y, ram, N, K, paradim, U):
"""
X :計画行列
y :測定値
ram :測定精度
N :粒子数
K :サンプル数
paradim:推定パラメータ数
U :一様乱数(0~1), numbaによる制約のため引数とした
"""
# Step.1:初期化
# 変数定義
np.random.seed(8)
chain = np.zeros((K, paradim))
S = np.random.randn(N+1, paradim)
S_mean = np.zeros(paradim)
S_replace = np.zeros((N+1, paradim))
q = np.zeros(N+1)
r = np.zeros(N+1)
# 平均、共分散行列及び提案分布から得られる対数確率密度の初期値の設定
for d in range(paradim):
S_mean[d] = S[:-1, d].mean()
S_cov = np.cov(S[:-1, :].T)
for n in range(N):
q[n] = target(X, y, S[n, :], ram)
# Step.2:サンプリング
cnt = 0
for i in range(K):
s = sampling(S_mean, S_cov, paradim)
q[-1] = target(X, y, s, ram)
for n in range(N+1):
S_replace[:, :] = S[:, :]
S_replace[n, :] = s
S_mean_replace = update_mean(S_mean, s, S[n,:], N)
S_cov_replace = np.cov(S_replace[:-1, :].T)
p = proposal(S_mean_replace, S_cov_replace, sita=S[n, :])
r[n] = p - q[n]
rmax = r.max()
r = np.exp(r - rmax)
r = r / np.sum(r)
# 棄却ステップ:J=N+1以外の場合は採択
c = 0
u=U[i]
for j in range(N+1):
c += r[j]
if c > u:
J = j
break
S_mean = update_mean(S_mean, s, S[J,:], N)
S[J, :] = s
S_cov = np.cov(S[:-1, :].T)
q[J] = q[-1]
if J != N+1:
chain[cnt] = s
cnt += 1
# Step.3:和集合に相当
chian = chain[:cnt-1, :]
return chain
4. Experiment
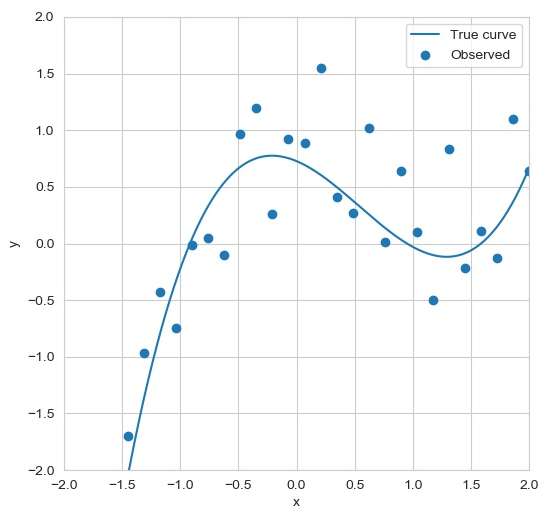
本実験ではベイズ線形回帰を対象とする。
(a) 実験用データ作成
# make data
def makedata(n, w_dim, vmin, vmax, seed, ram=0.0, Train=False):
np.random.seed(seed)
x = np.linspace(vmin, vmax, n)
w = np.random.uniform(-1, 1, w_dim)
X = np.zeros((n, w_dim))
for d in range(w_dim):
X[:, d] = x ** d
y = X @ w
if Train:
y += np.random.randn(n) / ram ** 0.5
return x, w, X, y
w_dim = 4
vmin = -2
vmax = 2
seed = 29
ram = 5
x_true, w_true, X_true, y_true = makedata(2000, w_dim, vmin-2, vmax+2, seed, Train=False)
x_train, _, X_train, y_train = makedata(30, w_dim, vmin, vmax, seed, ram, Train=True)
print(w_true)
# [ 0.72751997 -0.43018807 -0.85348722 0.52647441]
(b) SA-MCMC
%%time
sample_n = 10000
U1 = np.random.uniform(size=sample_n)
chain1 = SA_MCMC(X_train, y_train, ram, 100, sample_n, w_dim, U1)
U2 = np.random.uniform(size=sample_n)
chain2 = SA_MCMC(X_train, y_train, ram, 100, sample_n, w_dim, U2)
U3 = np.random.uniform(size=sample_n)
chain3 = SA_MCMC(X_train, y_train, ram, 100, sample_n, w_dim, U3)
# Wall time: 19.2 s
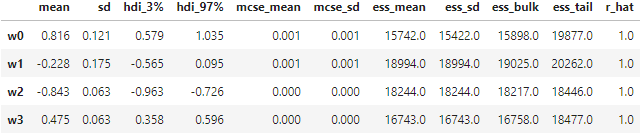
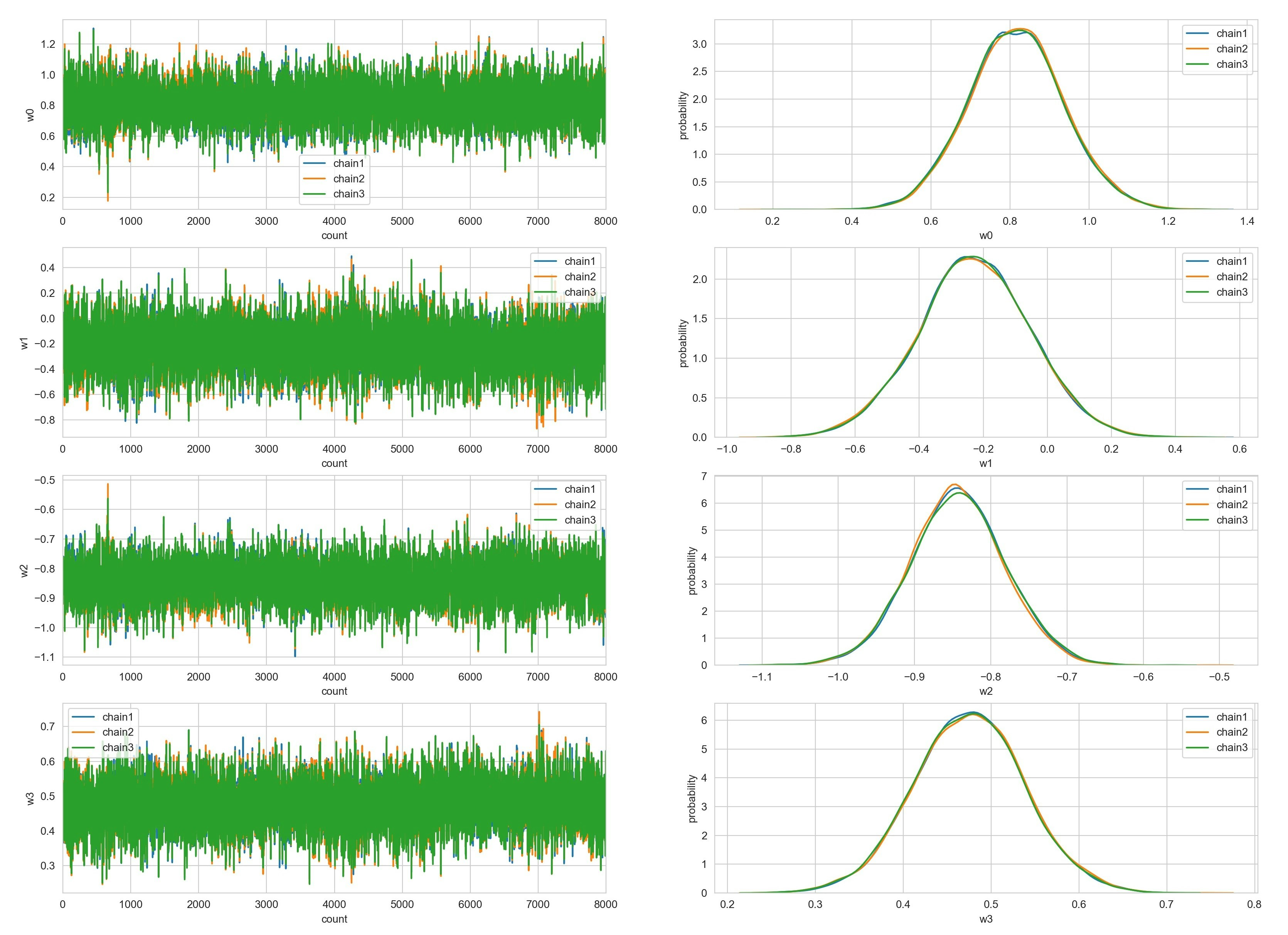
パラメータ推定結果は下記のとおり(burnin:2000)。有効サンプルサイズ(ess)が非常に大きい。目的分布による尤度評価は、1回のサンプリングあたりに1回であるが、粒子数$N$でパラメータ次元が$M$だとすると、尤度評価に加えて$O(NM^2)$の計算時間を要する。共分散行列の非対角成分を0にすることで、追加の計算時間を$O(NM)$に減少させることが可能であるが、その場合は性能が結構低下するようだ。
5. Summary
Sample Adaptive MCMCを実装してみました。いかがでしたか?