1.目的
本稿では、リッジ回帰にカーネル法及び乱択化フーリエ特徴(Random Fourier Features)を適用した回帰モデルを実装します。
一般的にリッジ回帰の学習時間は$O(N)$で高速なのですが、問題に応じた特徴量(基底関数)を設定する必要があります。これに対し、カーネル法を適用することで特徴量(基底関数)の設計が不要となりますが、学習時間は$O(N^2)$となります。したがいまして、教師データ数が多い(数万点)場合にはカーネル法の適用は困難です。
乱択化フーリエ特徴はカーネルを近似可能な基底関数を与え、これを用いることで学習時間は$O(N)$でありながら、カーネル法と同様に特徴量(基底関数)の設計を不要とすることが可能となります。
なお、リッジ回帰及びカーネル法については下記に導出も含めて詳細に記載されています。
https://qiita.com/wsuzume/items/09a59036c8944fd563ff
また、乱択化フーリエ特徴の概要については下記に概略があります。
https://tech.nikkeibp.co.jp/dm/atcl/mag/15/00144/00019/
2.リッジ回帰
最初に通常のリッジ回帰を実装してみます。リッジ回帰による回帰モデルは下式のとおりです。
\begin{align}
&f(x)=\sum_{m=0}^{M}w_{m}\phi_m (x)\\
&\phi_m (x)=x^m
\end{align}
ここで、$x$は入力、$w$は重み係数です。重み係数$w$は$N$個の教師データ$(x_1,t_1),(x_2,t_2)\dots(x_n,t_n)$及びハイパーパラメータ$\lambda$に基づき下式より得られます。
\begin{align}
&w=(\Phi^{T}\Phi+\lambda I)^{-1}\Phi^{T}\boldsymbol{t}\\
\\
&\Phi=\left(\begin{matrix}
\phi_1(x_1) & \phi_2(x_1) & \dots & \phi_M(x_1)\\
\phi_1(x_2) & \phi_2(x_2) & \dots & \phi_M(x_2)\\
\vdots & \vdots & \ddots& \vdots \\
\phi_1(x_N) & \phi_2(x_N) & \dots & \phi_M(x_N)\\
\end{matrix}
\right)
\boldsymbol{t}=\left(\begin{matrix}
t_1\\
t_2\\
\vdots\\
t_N
\end{matrix}
\right)
\end{align}
実装は下記のとおりとなり、1次元の場合は非常に簡単です。
import numpy as np
class RidgeRegression(object):
def __init__(self, lamda, M):
self.lamda = lamda
self.M = M + 1
def fit(self, X, t):
self.X = X
self.N = len(t)
Phi = np.zeros((self.N, self.M))
for n in range(self.N):
Phi[n, :] = self.func(X[n])
A = np.dot(Phi.T, Phi) + np.identity(self.M) * self.lamda
b = np.dot(Phi.T, t)
self.w = np.linalg.solve(A, b)
def predict(self, x):
return np.dot(self.w, self.func(x))
def func(self, x):
xlist = [x ** i for i in range(self.M)]
return np.array(xlist)
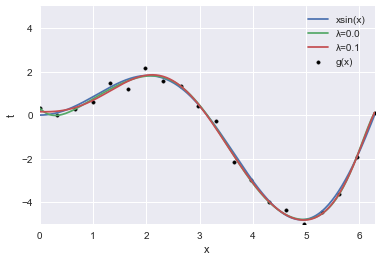
$g(x)=x\sin(x)+\varepsilon$に基づき作成された20点の教師データに対して得られた回帰曲線を示します。ここで、$\varepsilon$は平均0、分散0.2の正規分布です。ここでは、$M=10$、$\lambda=0,0.1$とします。本稿の検討で用いる試計算用データは非常に単純な関数から生成されているため、カーネル法を適用せずとも、多項式回帰で十分良くフィッテイングされます。
3.カーネル法
次にリッジ回帰にカーネル法を適用してみます。回帰モデルは下記のとおりです。ここでは無限次元の特徴量を考えていることに相当するガウスカーネルを用います。
\begin{align}
&f(x)=\sum_{n=1}^{N}\alpha_{n}k(x,x_n)\\
&k(x, x_n)=\exp(-\gamma(x-x_n)^2)\\
\end{align}
ここで、$\alpha$は重み係数ですが、先程のリッジ回帰とは$N$次元ベクトルとなっている点が異なります。また、$\lambda$、$\gamma$はハイパーパラメータです。重み係数$\alpha$は下式より得られます。
\begin{align}
&\alpha=(K+\lambda I)^{-1}t\\
&K=\left(\begin{matrix}
k(x_1,x_1) & k(x_1,x_2) & \dots & k(x_1, x_N)\\
k(x_2,x_1) & k(x_2,x_2) & \dots & k(x_2, x_N)\\
\vdots & \vdots & \ddots& \vdots \\
k(x_N,x_1) & k(x_N,x_2) & \dots & k(x_N, x_N)
\end{matrix}
\right)
\end{align}
実装は下記のとおりです。こちらも1次元の場合は非常に簡単に実装可能です。
import numpy as np
class KernelRegression(object):
def __init__(self, lamda=0.1, gamma=0.1):
self.lamda = lamda
self.gamma = gamma
def fit(self, X, t):
self.X = X
self.N = len(t)
x1, x2 = np.meshgrid(X, X)
dx = x1 - x2
K = self.func(dx)
A = K + np.identity(self.N) * self.lamda
self.alpha = np.linalg.solve(A, t)
def predict(self, x):
dx = self.X - x
k = self.func(dx)
return np.dot(self.alpha, k)
def func(self, dx):
return np.exp(-self.gamma * dx ** 2)
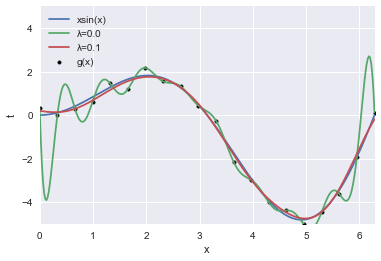
カーネル法により得られる回帰曲線を示します。ここでは、$\lambda=0,0.1$、$\gamma=1$とします。単純な関数形状から生成されたデータであるため、カーネル法適用による利得は皆無ですが、複雑で多次元な関数から生成されたデータに対して回帰モデルを作成する場合には、特徴量(基底関数)の設計が不要となるカーネル法の利得は大きくなります(ただし、正則化効果を調整しなければ酷い過学習状態となりますが)。
3.乱択化フーリエ特徴
最後に、乱択化フーリエ特徴を適用する場合を実装します。ガウスカーネルは乱択化フーリエ特徴により下記のように近似されます。また、$p(u)$は正規分布$N(0, s^2)$に従います。ここで、$u$は$p(u)$に従いランダムに$M$個サンプリングします。
\begin{align}
k(x, x_n)&=\int_{R}\exp(iu(x-x_n))dp(u)=\int_{R}\cos(u(x-x_n))dp(u)\\
&\approx\sum_{m=1}^M\cos(u_m(x-x_n))\\
&=\sum_{m=1}^M\cos(u_mx)\cos(u_mx_n)+\sin(u_mx)\sin(u_mx_n)
\end{align}
また、カーネルは下式に示すような基底関数に分解できます。
$$k(x, x_n)=\sum_{m=1}^{2M}\phi_m(x)\phi_m(x_n)$$
\begin{align}
&\phi_m(x)=\cos(u_mx)\quad (m=1,2,3\dots,M)\\
&\phi_m(x)=\sin(u_{m-M}x)\quad (m=M+1,M+2,M+3\dots,2M)\\
\end{align}
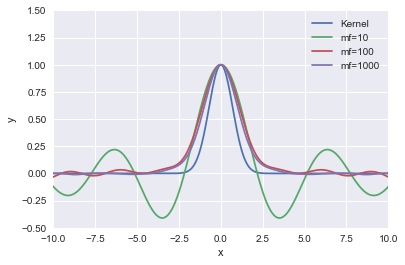
したがって、乱択化フーリエ特徴によりカーネルは有限次元の特徴量(基底関数)の内積として近似されます。この近似は、サンプリング数が少ない場合でもガウスカーネルをよく近似するそうです。実装の前に上記近似の妥当性について確認しました。サンプリング数$m=10,100,1000$としてガウスカーネルと比較したところ、100点程度サンプリングすれば良い近似となることが確認できました。ただし、サンプリング数が少ない場合は裾側で暴れます。また、$x=0$付近の形状も正規分布とは異なります。
乱択化フーリエ特徴を適用した実装は下記のとおりです。
import numpy as np
class RffRegression(object):
def __init__(self, lamda=0.1, sigma=1, mf=100):
self.lamda = lamda
self.sigma = sigma
self.mf = mf
self.u = np.random.normal(0, sigma*sigma, mf)
def fit(self, X, t):
self.X = X
self.N = len(t)
Phi = np.zeros((self.N, 2*self.mf))
for n in range(self.N):
Phi[n, :] = self.func(X[n])
A = np.dot(Phi.T, Phi) + np.identity(2*self.mf) * self.lamda
b = np.dot(Phi.T, t)
self.w = np.linalg.solve(A, b)
def predict(self, x):
return np.dot(self.w, self.func(x))
def func(self, x):
cosf = np.cos(self.u * x)
sinf = np.sin(self.u * x)
return np.hstack((cosf, sinf))
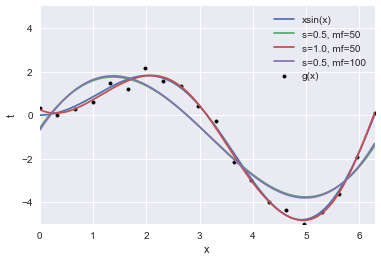
乱択化フーリエ特徴を適用した場合の回帰曲線です。ここでは、$\lambda=0.1$、$s=0.5,1.0$、$mf=50,100$とします。サンプリング数は少なくても良くフィッテイングできますが、少ない場合はフィッテイングの良し悪しは当然乱数に依存することになります。また、分散とサンプリング数でバイアス-バリアンスは調整可能ですが、ここら辺は未検討です。いずれにせよ、得られる回帰曲線が乱数による確率的なものであることには留意する必要があると思います。
4.まとめ
リッジ回帰にカーネル法及び乱択化フーリエ特徴を適用した場合の実装をしてみた。本稿では、試計算用データが単純な関数から生成されていることから、カーネル法適用による利得は見られなかったが、複雑多次元な関数に基づきデータが生成される場合には、特徴量(基底関数)の設計が不要となるカーネル法の導入による利得は大きなものとなる。したがって、カーネル法と同様の効果を大規模データにも適用可能な乱択化フーリエ特徴の適用は非常に有用であると考えられる。