はじめに
2022年のノーベル物理学賞は量子コンピュータの根底をなす量子もつれ(エンタングルメント)に関係する実証をしたアスペ等に贈られた。それ故、量子コンピュータがもっと騒がれるのかと思いきやそうでもない気が・・・そもそも充分騒がれているからか?それで、もつれにまつわるような投稿をアドベントカレンダーで投稿しようと考えていたところ、タイトルのようなナンセンスなことを思いついた。
最近、パブリックブロックチェーンでも情報を秘匿したいというニーズから、ゼロ知識証明(ZKP: Zero Knowledge Proof)なる、ひと昔前からある暗号技術が注目されているようだ。ゼロ知識証明とは、ウィキペディアからの引用では
ある人が他の人に、自分の持っている(通常、数学的な)命題が真であることを伝えるのに、真であること以外の知識を伝えることなく証明できるやりとりの手法
と。例えば、Pさんは金庫の鍵をもっているが、Vさんに鍵の実物を見せることなく、鍵を持っていることを証明すること等。Qiitaにもこのゼロ知識証明に関する投稿がちらほらあるが、専門家ではない私には @kenmaro 氏の「ゼロ知識証明」について解説!!が、分かり易かった。その中でも、あるいは先のウィキペディアの中でも、ジャン=ジャック・キスケータの「我が子にゼロ知識証明をどう教えるか 」というのがあり、これは洞窟の問題と言われている。この洞窟の問題の図を見ていたら、ふと本当は鍵を持っていないPさんが量子だったらこの問題はどうなってしまうのだろうというナンセンスなことが気になってしまった。
洞窟の問題
キスケータの文献ではアリババから始まり、現代へと変わる展開で面白いが、ここでは、そのエッセン部分のみを都合に合わせて説明する。
下の図1のような入口が一つで途中でAルートとBルートに分岐しており、それが奥で繋がっている洞窟を考える。AとBの繋がっているところには、ドアがあり、それは鍵を持っていないと開かない。図ではそれを鍵絵のついた黒のブロックで示している。

Pさんは、実は鍵を持っているが、その鍵自体はVさんに見せたくない。が、Vさんに持っているという事実は証明したい。そのためにまずPさんは洞窟に入りAまたはBルートを進む。この時、VさんはPさんがどちらのルートに進んだかはわからない。最奥のドアにさしかかった時に、ドアのそばにはスピーカーがあり、Vさんから「Aルートから戻れ」または「Bルートから戻れ」とPさんは指示を受ける。Aルートを進んでいった場合、Vさんの指示がAルートであれば鍵を使わずにAルートから戻られるし、指示がBルートであったとしても、当然、Pさんは鍵を持っているので、鍵を開けてBルートから戻ることが可能である。つまり、鍵をもっているPさんは、はじめにどちらのルートから進もうが、このことを何回繰り返しても、必ずVさんの指示したルートから戻ることができる。尚Vさんはこの時は入口から洞窟を覗いていてPさんがどちらのルートから戻ってきたかを確認できる。
もしPさんが鍵を持っていなかったとしたら、指示に従える確率は1/2である。このことをn回繰り返した場合、指示通り戻ることができる確率は$(1/2)^n$であり、例えばnが8回だとすれば確率は0.004、つまり実質ゼロとなる。このことより例えばPさんが8回中8回指示通りに戻ってこられたらPさんはVさんに鍵を見せないでも鍵を持っていることを実質的に証明できたことになる。・・・初めからVさんがPさんにAルートから進みBルートから戻ってくるように指示すれば事足りるのでは?この場合、Pさんが不正をしないように、VさんはPさんがAルートから進むことを見届ける。逆にVさんはPさんの後をこっそりつけて、ドアの前でPさんが鍵を使うのを目撃できてしまう恐れがある。
トンネル効果が使えたら
実はPさんは鍵を持っていないとする。そして鍵のないPさんはドアの前まで来る。ここまでは普通である。がここでPさんは突如、量子となってしまう。ここで、Vさんはどちらか一方から戻るようにPさんに指示。その指示に従って、Pさんは指示された側にそもそも居るのであればそのまま引き返すし、もし、指示された側ではない側に居た場合は、Pさんは量子化しているので、ドアの鍵を開けなくてもトンネル効果でドアをすり抜けてしまうことができ指示に応じたルートで戻ることができる。その後Pさんは量子からまた古典的実在に復帰する・・・Pさんは鍵を持っていなくてもこれでVさんに鍵を持っていることを証明できてしまう???
否、トンネル効果の場合、全てがすり抜けるのではなくドアのサイズ(高さや厚み)やPさんのエネルギーや質量によって、どの程度すり抜けられるのか、つまり透過率が決まり、透過できなかった分は反射、つまり元のルートに戻ることになる。
がそもそも、トンネル効果をゲート型コンピュータでどう扱うのか全く知らないし。それ以前に、ゲート型の量子コンピュータで洞窟問題をどうモデル化するのか?まずはそこから。
洞窟の問題の量子コンピュータモデル
量子コンピュータ的にどうモデル化するのか?まず洞窟の経路は図2のようなセルの繋がりと考える。セルの一つ一つを一つのqubitで表し、Pさんは、このセル上の、つまりあるqubitでの'1'として表す。こうすることにより、Pさんの動きはセル上での移動として表すことができ、あたかもセルオートマトンのように見立てていくことができる。こうすれば、例えばセルオートマトンのウルフラムコードのルール184(つまり渋滞系)などで前進させていくことができる。ただし、セルオートマトンと異なり、動かすのはPさんのみである。尚、ウルフラムコードやセルオートマトンについては、4回目 セルオートマトンの量子アルゴリズムを、ルール184については5回目 セルオートマトンの量子アルゴリズムをそれぞれ参照されたし。で、ルール184の場合、自分の前のセルが空いていれば進める、逆に前のセルが既に埋まっていれば進めないというルールである。だとすると、最奥のドアのセルが埋まっていれば(このセルは動かさない)、Pさんはここで前進できなくなる。ここで登場するPさんは鍵を持っていないので、Vさんの指示後、もと来たルートを引き返さざるを得ない。Vさんの指示のさせ方は後述する。ここまではqubitを使ってはいるがPさんは1という古典的実在のままである。ここから、Pさんそのものを量子化してみよう。その狙いはPさんを量子化させることによって、重ね合わせにより両ルートにPさんを存在させ常にVさんの指示通りの戻り方ができるようにするためである。
古典的な実在のPさんを量子化するのはPさんのいるセルのqubitにアダマールゲートを適用することに他ならない。するとPさんは、'1'と'0'が均一に重ね合わせされた状態となる。観測をするとPさんが「いる」場合と「いない」場合が半々の確率で出現することになる。この重ね合わせを、少し工夫をして、AルートとBルートにPさんを割り振ることを考える。仮にAルートに'1'を割り振ると、Bルートには'0=いない'を割り振ることになる。'0=いない'では結局いないことになってしまい割り振りの意味がないので、この'0=いない'は反転させ、強制的に'1=いる'にする。では、そもそもAルートのPさんをBルートに振り分けるのはどうするのか。これはAルートのPさんをBルートにコピーすることで実現する。ここまでのプロセスを図3とともに整理し、またblueqatのコードを記載する。
➀ Pさんのいる X qubitにアダマールゲートを適用する c.h[X]
➁ このqubitの内容を反対側のルートの Y qubitにコピーする c.cx[X,Y]
➂ コピーされたY qubitを反転(フリップ)させる c.x[Y]
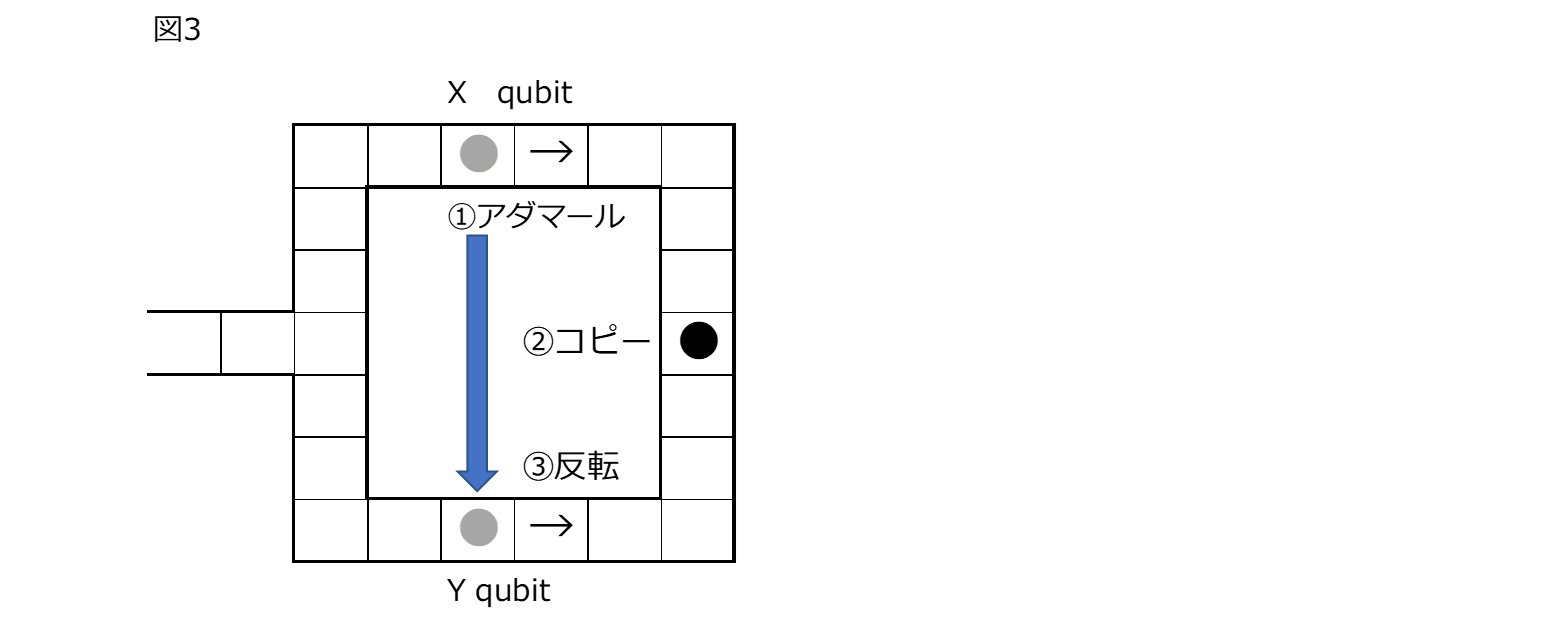
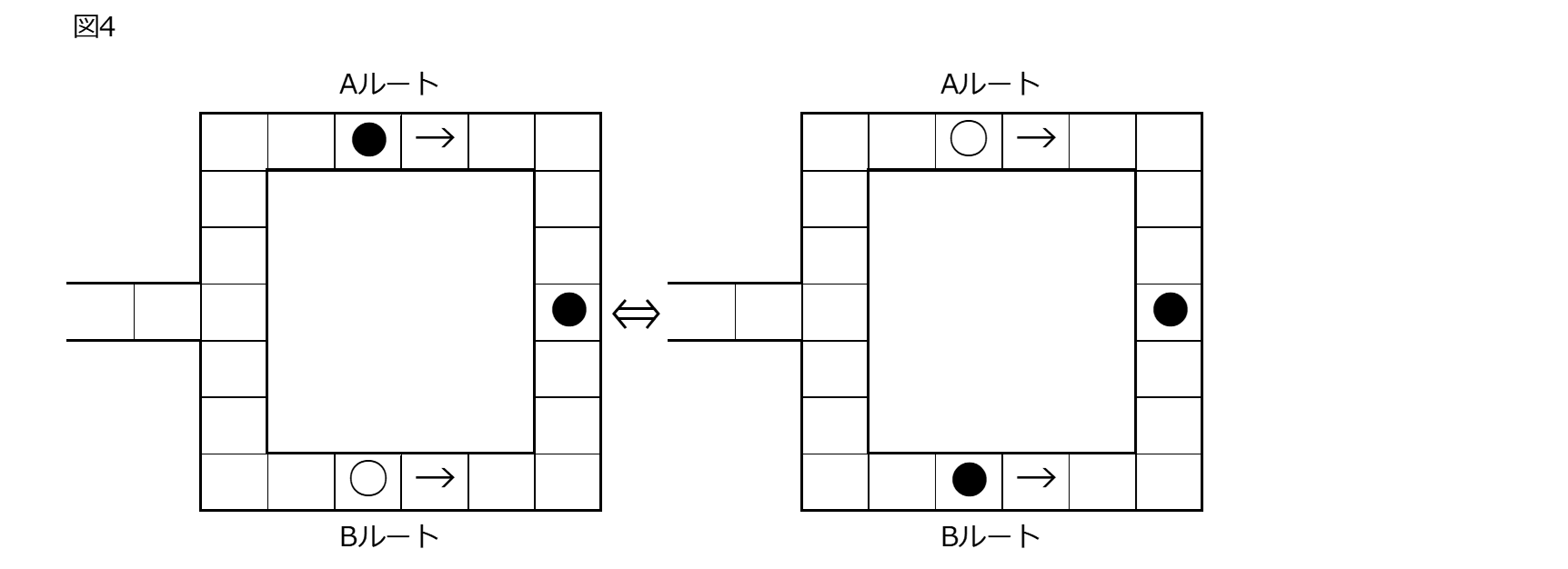
➁のコピーは制御NOTゲートで実施しているので、これは、X qubitとY qubit間でエンタングルメントさせたことに他ならない。だとすると、もしAルートのPさんが何かの拍子でフリップするとBルートのPさんも同時にフリップすることになる。➁の段階ですでに両qubit間はエンタングルメントしているので➂の操作をすればもとのX qubitも反転するはずである。従って図3の状態で観測をすると、Pさんが「いる」を黒丸●、「いない」を白丸○で現した図4のいずれか一方の状態が必ず観測されるはずで、どちらも黒丸●であったり、どちらも白丸○であるような状態は現れないはずである。つまり、➀➁➂をすることによって、図4の二つの絵の状態が重ね合わさっていると考えられる。
以下の非常に簡単なコードで確かめてみる。図3のX qubitを第0qubit目とし、Y qubitを第1qubit目として、100回試行した結果をコードの下に表示した。
from blueqat import Circuit
c=Circuit(2)
c.x[0] #AルートのPさんを'1=いる'とする
c.h[0] #AルートのPさんを量子化
c.cx[0,1] #AルートのPさんをBルートにコピー
c.x[1] #Bルートを反転
ans=c.m[:].run(shots=100)
print(ans)
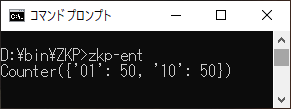
ご覧通り'10'と'01'がほぼ半々で観測されるが、'11'や'00'は全く出現しない。つまり、右ルートにPさんが「いる」時には左ルートには「いない」し、右ルートにPさんが「いない」ときには左ルートに「いる」。この二つの状態が重ね合わさっていると言えよう。
Vさんの指示
Vさんの指示をモデルに如何に組み込むか少々悩むところである。ここで、ずるいと思われる方もいるかもしれないが、グローバーアルゴリズムのマーキングを適用してみる。今、Pさんは洞窟を進んで最奥のドアの前に来て進めなくなった状況を図5に示した。ここで、Aルート側のPさんのいるセルをqubitのa、Bルート側のPさんのいるセルをqubitのbとしよう。またドアのセルをqubitのcとしよう。
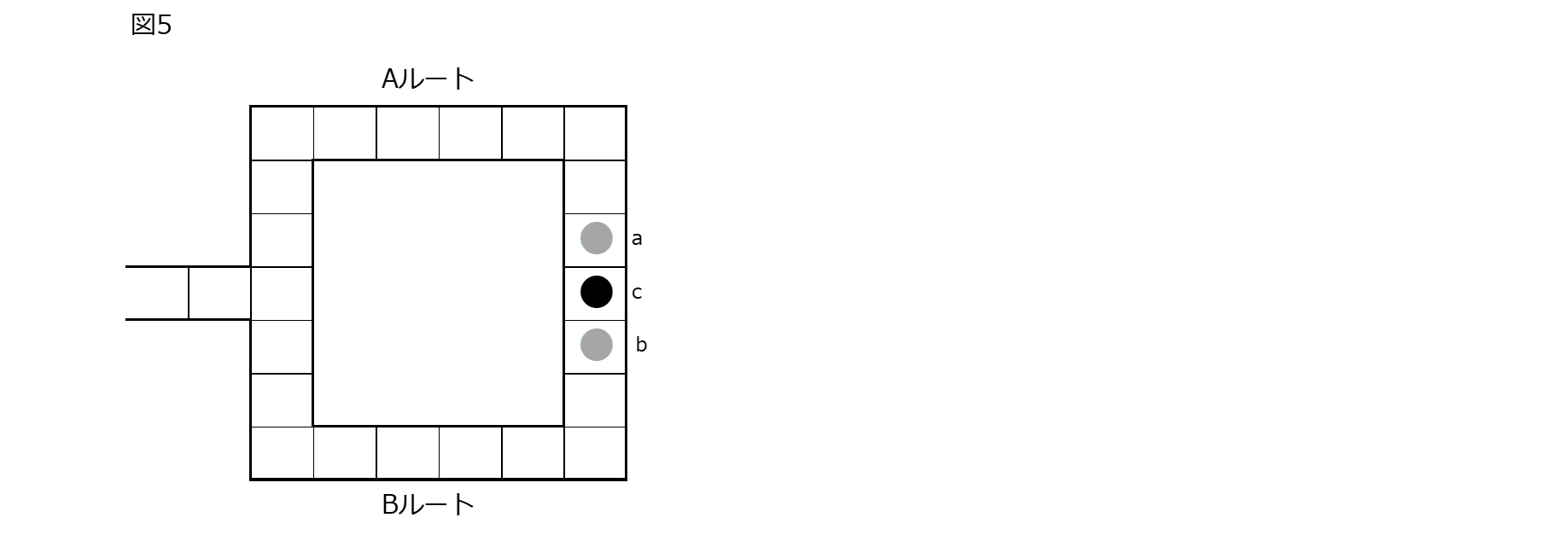
Vさんの指示を、もし「Aルートで戻れ」であれば、aを'1'とし、bを'0'としたベクトルで表現しよう。つまり(a,b)=(1,0)。「Bルートで戻れ」であれば(a,b)=(0,1)である。これをグローバーアルゴリズで言うこの状態ベクトルをマーキングすることで指示の履行を行う。マーキングとは、この状態ベクトルのみ、他の状態ベクトルとは異なる位相に反転、つまり異なる符号を付与、させることである。式で表すと以下の通りである。$k_i$を正の係数としており、(a,b)=(1,0)に相当する、第3項の符号のみ負にしている。
$$ψ=+k_1|00>+k_2|01>\boldsymbol{-k_3}|10>+k_4|11>(式1)$$
グローバーアルゴリズのマーキングや後述する増幅に関しては、7回目 グローバーアルゴリズ一考を参照されたし。
Pさんの帰還
Vさんの指示はグローバーアルゴリズムでのマーキングを用いることにしたので、Pさんの帰還はグローバーアルゴリズムでの増幅を適用しよう。であれば、Vさんの指示した状態ベクトルが増幅されるので、ドアに無関係にPさんは当然、Vさんの指示通りの側に存在できることになろう。が、そうはいかない!
具体的なコードと簡単な式で上手くいかないことを示そう。以下に、シナリオとして、PさんはAルートに入り、VさんはBルート帰還を指示、というblueqatのコードとその結果を示した。尚、aを第0qubit、bを第1qubitとしている。
from blueqat import Circuit
import numpy as np
import math
c=Circuit(2) #以下、シナリオ
c.x[0].h[0] #AルートのPさんを実在化させ、その後、量子化
c.cx[0,1] #Bルートへコピー:エンタングルメント
c.x[1] #BルートのPさんを反転
c.s[1].cz[0,1].s[1] #Vさんの指示(Bルートで帰還せよ)でB側 |01>をマーキングのつもり
c.h[:].x[:].cz[0,1].x[:].h[:] #増幅
ans=c.m[:].run(shots=100)
print(ans)
ご覧の通り、観測の結果は、何故か|00>と|11>が半々である。これは定石通りのグローバーアルゴリズムと異なり、マーキング後の状態は以下の式2のようになっている。エンタングルメントによりそもそも1項と4項は存在しないし、増幅させたい3項も位相反転していない。
ψ=+0|00>+1/\sqrt{2}|10>+1/\sqrt{2}|01>+0|11>\\
=\boldsymbol{+1/\sqrt{2}|10>+1/\sqrt{2}|01>}(式2)
この状態では正しい増幅は行われない。
そこで、少し工夫が必要となる。増幅やマーキングのための工夫として図5のc、つまりドアをベクトルに加えてみる。cは勿論'1'である。Vさんの指示が「Aルートで戻れ」であれば、(a,c,b)=(1,1,0)、逆に「Bルート側で戻れ」であれば、(a,c,b)=(0,1,1)となる。これらの状態ベクトルをマーキングすることで指示する。以下にコードを記す。
from blueqat import Circuit
import numpy as np
import math
c=Circuit(3) # a(A側)を第0qubit、c(ドア)を第1qubit、b(B側)を第2qubit
c.x[1].x[0] # ドアの設定とPさんをAルートで実在化
c.h[0] # Pさんの量子化
c.cx[0,2].x[2] # Bルートへのコピーと反転
c.x[2].h[2].ccx[0,1,2].h[2].x[2] # 1回目のマーキング Bルート戻りを指示 |011>マーキングのつもり
c.h[:].x[:].h[2].ccx[0,1,2].h[2].x[:].h[:] # 1回目の増幅
c.x[2].h[2].ccx[0,1,2].h[2].x[2] # 2回目のマーキング Bルート戻りを指示 |011>マーキング
c.h[:].x[:].h[2].ccx[0,1,2].h[2].x[:].h[:] # 2回目の増幅
ans=c.m[:].run(shots=100)
print(ans)
1回目のマーキング後ではどのような状況になっているのであろう?実は式3のようになる。
ψ=+1/\sqrt{2}|110>+1/\sqrt{2}|011> (式3)
あれ、マーキングはおろか、エンタングルで|110>と|011>しか存在しない。これでは先ほどと同じである。が、しかし 1回目の増幅後はと言うと、
ψ=+1/\sqrt{8}|000>+1/\sqrt{8}|100>+1/\sqrt{8}|010>\boldsymbol{-1/\sqrt{8}|110>}\\
+1/\sqrt{8}|001>+1/\sqrt{8}|101>\boldsymbol{-1/\sqrt{8}|011>}+1/\sqrt{8}|111>(式4)
おお、なんと全状態ベクトルが現れ、|110>と|011>の符号が反転した状態となる。この状態で2回目のマーキングをしてみる。すると
ψ=+1/\sqrt{8}|000>+1/\sqrt{8}|100>+1/\sqrt{8}|010>+1/\sqrt{8}|110>\\
+1/\sqrt{8}|001>+1/\sqrt{8}|101>\boldsymbol{-1/\sqrt{8}|011>}+1/\sqrt{8}|111>(式5)
となり、|011>の符号のみが反転している状態となる。これなら|011>のみが増幅される。で、最終的な結果はというと

ご覧の通り、100回のショットで7割強から9割近く、011が出現する。理屈上の振幅確率は78%である。つまり、鍵を持っていなくてもPさんは8割がたVさんの指示通りの帰還を果たせることを意味している。
Pさんを量子にした挙句とトンネル効果
1回の洞窟トライで鍵を持たないPさんがVさんの指示通り戻れる確率は、古典Pさんでは50%、量子Pさんでは78%である。量子Pさんはすごいのか、あるいは古典とさして変わらないのか?もし8回トライした後でもVさんを欺ける可能性は、古典では、0.4%・・・1/250、一方、量子では14%・・・1/7・・・存外、高確率。が、しかし、鍵があればこれは100%。Pさんを量子にした価値とは一体何だったのであろう?
唐突ながらトンネル効果でも所詮100%のドアのすり抜けはできないとこの投稿の初めの方で書いたことを思い出して欲しい。そして、すり抜けられる確率、つまり透過率はPさんの条件を固定すれば、ドアの厚みに依存。(洞窟の場合ドアの高さは洞窟断面全面にドアが広がっているので一定)そう、ドアはポテンシャルバリアに相当する。今回の洞窟の問題のPさんのVさんの指示に対する成功率の古典に対する上昇率は、いわばドアのトンネル効果と考えられないだろうか。するとドアのポテンシャルを変えるとPさんの透過率はどうなるのであろうかと気になる。ドアのポテンシャルはこのモデルでは以下の図6のようにドアに相当するセル数を増やすことになろう。
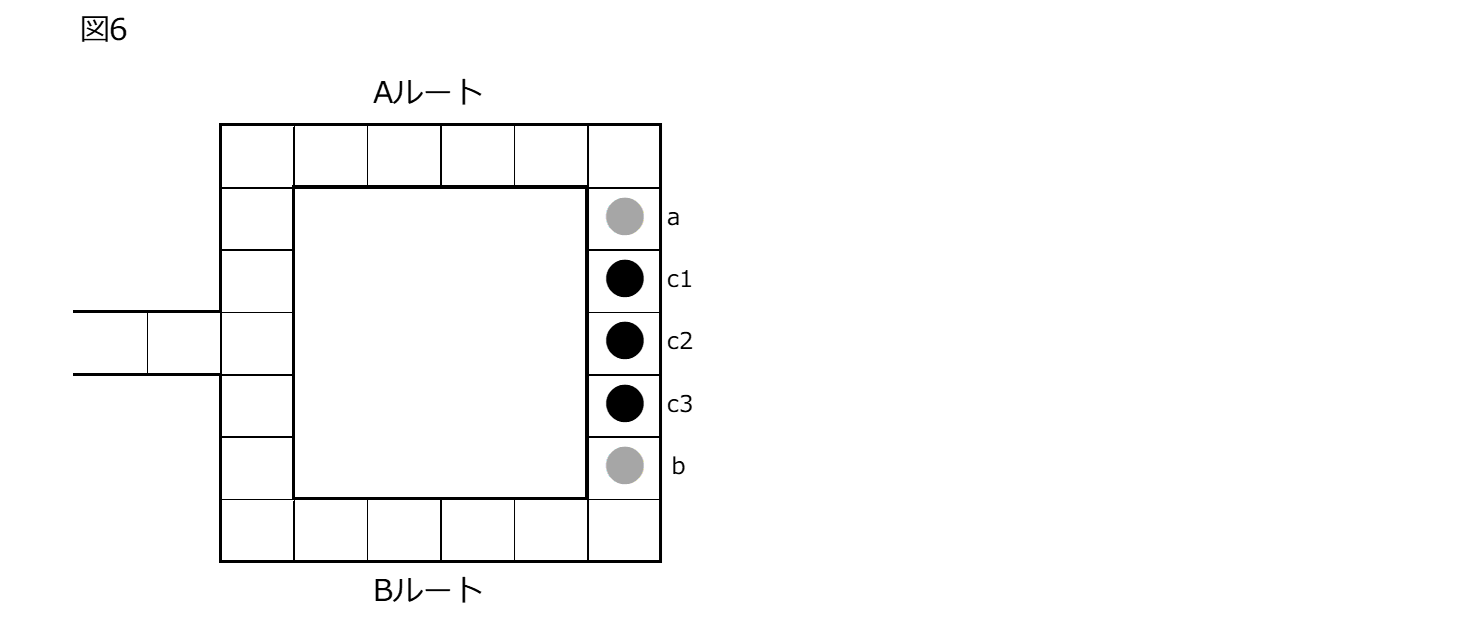
結論から言おう。このようにドアの厚みを増していくと、グローバーアルゴリズムで増幅できる最高値の振幅は減ってくる。ただし、ドアの厚みが奇数の時のみで、偶数の時は式2から発展せず増幅はされない。が奇数の時のみとは言え、いうなればポテンシャルバリアを増加させると透過率が減ってくるように見える、あたかもトンネル効果のように。
Pさんの持つべき鍵は?
最後に、Pさんは鍵を持っていないことが前提だが、もし今回のモデルでPさんが鍵を持っているとしたら、それはどんな鍵であろうか?