TeX言語で型なしλ計算を評価するVMを書いた話

※本記事では型なしλ計算は多少程度知っている前提とします．

概要

半ばネタOSSとして実装した tex_of_ocaml¹ について簡単に紹介します．以下のリポジトリで実装を公開しています（執筆時点での最新のcommit hashは e6e3997）：

GitHub - gfngfn/tex_of_ocaml: A compiler for untyped lambda terms to TeX code

これは以下の2つの構成要素からなっています：

OCaml風の構文をもつ型なしラムダ項をTeX言語コードへとコンパイルする，Rust製の小さいコンパイラ
1のコンパイラから吐かれるコードを評価するTeX言語製のVM（＝バイトコードインタプリタ）

1はあまり非自明なことをしておらず，かなり単純なコンパイラです²．非自明なのは2で，これは SECDマシン³ と呼ばれるVMを，TeX言語で 完全展開 によって評価が進む（すなわち，簡単に言えば \edef による定義の中で使える）ような形で実装したものです．

こうして型なしλ計算は完全展開可能な処理に限定したTeX言語コードにもエンコードすることができ，TeX言語は完全展開だけでTuring完全性をもつらしいことが体現できました．

動作例

リポジトリ直下で以下のように動かせます：

入力を用意する

リポジトリに置いている例を使いましょう：

examples/example3.txt

(fun x -> fun f -> f (arabic (add 1 x))) 42 (append "foo")

add は自然数の加算，arabic は自然数から十進文字列への変換，append は文字列結合です．

出力の準備

出力先ディレクトリ _generated/ を準備します．ここにVMの実装である secd.sty を置いておきます（このファイルもコンパイラに自動で出力させればいいのですが，サボってやっていません）：

$ mkdir -p _generated
$ cp src_tex/secd.sty _generated

コンパイルする

$ cargo run examples/example3.txt -o _generated/example3.tex

ちなみに中身を見てみると以下のようなコードが出ています：

実行

評価を走らせ，処理結果のPDFを得ます：

$ cd _generated
$ latexmk example3.tex

これを行なうと _generated/example3.pdf に結果のPDFが出力され，見てみると以下のようになっています：

たしかに (fun x -> fun f -> f (arabic (add 1 x))) 42 (append "foo") の計算結果である "foo43" という文字列が出ていることがわかります．ちなみに最終結果は文字列だけでなく整数や真偽値でも適切に表示します⁴．

もっと複雑な計算もできて，例えば階乗の計算も可能です．以下を入力とすると⁵，

examples/factorial.txt

let fix = (fun f -> (fun x -> f (fun v -> x x v)) (fun x -> f (fun v -> x x v))) in
let fact = fix (fun f -> fun n -> if iszero n then 1 else mult n (f (sub n 1))) in
fact 5

以下のゴチャッとしたLaTeXコードが出てきて，

処理すると意図通り次のような計算結果の載ったPDFが出てきます：

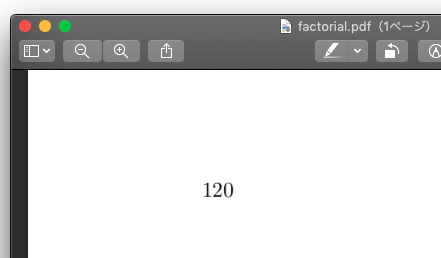
やったぜ．

完全展開とは

念のためTeX言語での展開制御に親しみのない方向けに説明すると，完全展開 とは簡単に言えばTeX処理系がTeX言語プログラムを処理する過程に於いてレジスタへの代入をはじめとする種々の “手続き的な処理” を行なわずに飛ばして展開（≒項書き換え）のみを行なうことであり，例えば \edef〈Command〉{〈Tokens〉} による定義では定義の右辺に相当する部分 〈Tokens〉 が完全展開によって書き換えられた結果がコマンド 〈Command〉 の書き換え後の列と定義されます．完全展開中で展開できないトークンに出会った場合は単にそれを “処理する必要のないもの” として読み飛ばす⁶ ので，完全展開が行なわれる文脈では “純粋函数的な処理” となります．

SECDマシンとは

詳細は言語処理系の論文や教科書を読めばあると思いますが，SECDマシン³ はラムダ計算やそれに準ずる言語のプログラムを評価するVMを実現する方法のひとつで，その名の由来になっている通り $S$ (Stack), $E$ (Environment), $C$ (Code), $D$ (Dump) の4つ組の書き換え規則として定式化されています．これは次のような形式をとります：

\begin{align}
  &\text{stacks}       & S &::= [V]^{*}\\
  &\text{environments} & E &::= [V]^{*}\\
  &\text{code}         & C &::= [I]^{*}\\
  &\text{dumps}        & D &::= [(C, E)]^{*}\\
  &\text{values}       & V &::= c\ |\ \langle C, E\rangle
\end{align}

ただし，$[X]^{*}$ は $X$ が動く範囲のものを0個以上有限個並べた列を動くことを表し，$c$ は整数や真偽値などの定数を動くとします．$I$ は インストラクション と呼ばれる “VMに於ける命令の最小単位” であり，以下で定義されます⁷：

\begin{align}
  &\text{instructions} & I &::=\\
  &&&|\ \mathrm{Access}(i)\\
  &&&|\ \mathrm{Closure}(C)\\
  &&&|\ \mathrm{Apply}\\
  &&&|\ \mathrm{Return}\\
  &&&|\ \mathrm{Const}(c)\\
  &&&|\ \mathrm{Prim}(p)
\end{align}

ここで $i$ はインデックスと呼ばれる機構で変数に相当し，自然数⁸を動きます．また，$p$ はプリミティヴ，すなわち整数の加算 $+$ や真偽値の論理積 $\land$ などといった，定数上の計算の方法を表したものを動きます．プリミティヴは各々アリティ（＝引数を何個とるか）をもち，$p$ のアリティを $\mathrm{arity}(p)$ と書くことにします．また $p(V_1, \ldots, V_n)$ でその計算結果を表すことにします（例えば $+(42, 57) = 99$）．

直観を説明すると，$S$ は計算中に用いる値がスタックとして積み重なっているもので，これは（スタックという名前が示す通り）上（＝手前）からしか値を出し入れしない機構です．$E$ は環境で，変数に相当するインデックスに対してそれがどんな値であるかを保持しています．これはランダムアクセスされる機構です．コード $C$ はインストラクション列であり，以下で見るように各インストラクションは次の書き換え処理を指示します．変換規則は後述しますが，この $C$ がユーザの書いたプログラムからコンパイラによって変換されて出てくるものです．$D$ は退避場所であり，“函数の呼び出し中に復帰後のコードと環境を保持しておく” という役割を果たします．

上記の直観を形式化して述べると，SECDマシンはコード $C$ の評価にあたり $(\epsilon, \epsilon, C, \epsilon)$ を初期状態として以下の評価規則による書き換えを繰り返します（ただし $\epsilon$ は空列，$(-) \cdot (-)$ は列の結合を表します）：

\begin{align}
  (S, E, \mathrm{Access}(i) \cdot C, D) &\longrightarrow
    (E[i] \cdot S, E, C, D)
\\
  (S, E, \mathrm{Closure}(C') \cdot C, D) &\longrightarrow
    (\langle C', E\rangle \cdot S, E, C, D)
\\
  (V \cdot \langle C', E'\rangle \cdot S, E, \mathrm{Apply} \cdot C, D) &\longrightarrow
    (S, V \cdot E', C', (C, E) \cdot D)
\\
  (S, E, \mathrm{Return} \cdot C, (C', E') \cdot D) &\longrightarrow
    (S, E', C', D)
\\
  (S, E, \mathrm{Const}(c) \cdot C, D) &\longrightarrow
    (c \cdot S, E, C, D)
\\
  (V_n \cdot \cdots \cdot V_1 \cdot S, E, \mathrm{Prim}(p) \cdot C, D) &\longrightarrow
    (p(V_1, \ldots, V_n) \cdot S, E, C, D)\quad(\text{where}\ n = \mathrm{arity}(p))
\end{align}

ただし $E[i]$ は “$E$ の $i$ 番目の値を取り出したもの” で，以下のように定義されます：

\begin{align}
  (V \cdot E)[0] &:= V
\\
  (V \cdot E)[j + 1] &:= E[j]
\end{align}

上記の評価規則について直観を添えておくと，$\langle C, E\rangle$ の形の値は クロージャ と呼ばれ，“計算 $C$ とそのための環境 $E$ が凍結されたもの” です．λ抽象に相当するインストラクション $\mathrm{Closure}(C)$ はコード $C$ とそのときの環境 $E$ からクロージャをつくってスタックに積む命令です．$\mathrm{Apply}$ は函数呼び出しに相当し，そのときのスタックの頂上から引数を，そのひとつ下から “呼び出され待ちの函数” にあたるクロージャを取り出して適用します．

そして最終的に $(V, E, \epsilon, \epsilon)$ の形で書き換えられなくなったら $V$ が計算結果です．これ以外の形で書き換えられなくなった場合は不正な計算です（型なしの言語でいう動的エラーです）．また，書き換えが停止しないこともありえます（所謂無限ループに相当します）．

以上がSECDマシンというVMの定式化であり，後述するように今回TeX言語で実装したものです．

コンパイラによるプログラムからVMのコードへの変換

SECDマシンの初期状態の $C$ にあたるコードはコンパイラが出力します．これは次のような2段階の変換を経ます（これも学部生向けの一般的な教科書などで触れられているような内容だと思います）：

ユーザの書いたプログラムを受け取り，変数名をなくした de Bruijn表現 へと変換する
1で変換した結果のde Bruijn表現を受け取り，VM用コードに変換する

1は簡単に言えば変数を de Bruijnインデックス という番号による参照に置き換える処理です．まず，通常のλ項とde Bruijn表現の構文はそれぞれ以下の $e$ と $t$ で定義されます：

\begin{align}
  e &::= x\ |\ \lambda x.\ e\ |\ e\ e\ |\ c\ |\ p([e]*)
\\
  t &::= i\ |\ \lambda.\ t\ |\ t\ t\ |\ c\ |\ p([t]*)
\end{align}

ここで出てくるde Bruijnインデックス $i$ は自然数で，簡単に言えば “何重の外側のλによってその変数が束縛されたか” を表します．変換は例を見ればわかりやすいと思います：

$(\lambda x.\ \lambda y.\ x\ y)$ ↦ $(\lambda.\ \lambda.\ 1\ 0)$
$(\lambda x.\ \lambda y.\ (\lambda z.\ z\ x)\ y)$ ↦ $(\lambda.\ \lambda.\ (\lambda.\ 0\ 2)\ 0)$

これを一般化した変換規則が以下で，通常の変数名をもつλ項 $e$ に対応するde Bruijn表現は $\mathrm{dB}(e)$ で定義されます：

\begin{align}
  \mathrm{dB}(e) &:= \mathrm{dB}(\epsilon, e)
\\
  \mathrm{dB}(w, x) &:=
    \mathrm{Index}(w, x)
\\
  \mathrm{dB}(w, \lambda x.\ e) &:=
    \lambda.\ \mathrm{dB}(x \cdot w, e)
\\
  \mathrm{dB}(w, e_1\ e_2) &:=
    \mathrm{dB}(w, e_1)\ \mathrm{dB}(w, e_2)
\\
  \mathrm{dB}(w, c) &:=
    c
\\
  \mathrm{dB}(w, p(e_1, \ldots, e_n)) &:=
    p(\mathrm{dB}(w, e_1), \ldots, \mathrm{dB}(w, e_n))
\\
  \mathrm{Index}(y \cdot w, x) &:= 1 + \mathrm{Index}(w, x)\quad(\text{if}\ y \neq x)
\\
  \mathrm{Index}(x \cdot w, x) &:= 0
\end{align}

2のde Bruijn表現からバイトコードへの変換もそれほど複雑ではなく，de Bruijn表現 $t$ に対して以下の変換でVM用バイトコード $\lfloor t\rfloor$ が得られます：

\begin{align}
  \lfloor i\rfloor &:=
    \mathrm{Access}(i)
\\
  \lfloor \lambda.\ t\rfloor &:=
    \mathrm{Closure}(\lfloor t\rfloor \cdot \mathrm{Return})
\\
  \lfloor t_1\ t_2\rfloor &:=
    \lfloor t_1\rfloor \cdot \lfloor t_2\rfloor \cdot \mathrm{Apply}
\\
  \lfloor c \rfloor &:=
    \mathrm{Const}(c)
\\
  \lfloor p(t_1, \ldots, p_n) \rfloor &:=
    \lfloor t_1\rfloor \cdot \cdots \cdot \lfloor t_n\rfloor \cdot \mathrm{Prim}(p)
\end{align}

以上がユーザの書いたλ項のプログラム $e$ をVMバイトコード $C := \lfloor\mathrm{dB}(e)\rfloor$ に変換する過程です．

どうやってVMをTeX言語で完全展開可能に実装したか

で，肝腎のVMをどうやってTeX言語で完全展開可能になるように実装したかですが，SECDマシンを知っていてTeX言語の展開制御に慣れているなら，大域的な実装方針としては意外に変態技巧を要する箇所はありません．実装を見てもらうのが早いですが，思ったよりは読めるTeX言語コードになっていると思います（大量にコメントを書いたので，一般的なTeX言語コードに比べると読めると思います）：

参考： tex_of_ocaml/secd.sty at e3f146e9d76f898a81e3ef62555a2413c1d26266 · gfngfn/tex_of_ocaml · GitHub

VMの定義自体は370行目で終わっており，それより後ろは全てプリミティヴの定義です．VMの処理としては以下の \secd@Run が根幹で，\secd@Run{〈S〉}{〈E〉}{〈C〉}{〈D〉} の展開が行なわれることで $(S, E, C, D)$ から次の状態へと遷移してまた \secd@Run が展開されるに至り，それを繰り返してやがて（うまくいけば） $C$ が空列になって停止します．

\def\secd@Run#1#2#3#4{%
  %% #1 : stack
  %% #2 : environment
  %% #3 : code
  %% #4 : dump
  （中略）
}

内部表現

内部表現についても実装の冒頭のコメントにメモしていますが，主な特徴をここにも記しておきます．

まず $S$, $E$, $C$, $D$ については結構素直で，単に要素を並べただけだったりします（以下では ［X］ で X の0個以上有限個の列を表すとします）：

〈Stack〉 ::= ［〈Value〉］

〈Environment〉 ::= ［〈Value〉］

〈Code〉 ::= ［〈Instruction〉］

〈Dump〉 ::= ［\secd@DUMP{〈Code〉}{〈Environment〉}］

値は以下のように先頭にタグとなる制御綴，末尾に終端を示す制御綴，その間にエンコードされた値を置く，という形式をとっています：

〈Value〉 ::=
   | \secd@CLOS{〈Code〉}{〈Environment〉}\secd@ENDVAL
   | \secd@INT{〈Number〉}\secd@ENDVAL
   | \secd@BOOL{〈Bool〉}\secd@ENDVAL
   | \secd@STRING{〈String〉}\secd@ENDVAL

この先頭のタグが展開不能（具体的には \relax に \let されている）のが \romannumeral による先頭完全展開を停止させる仕組みとして結構重要だったりします．

インストラクションもわりと素直ですが，いずれも1引数限定という形式をとっています：

〈Instruction〉 ::=
  | \secd@ACCESS{〈Index〉}
  | \secd@CLOSURE{〈Code〉}
  | \secd@APPLY{}
  | \secd@RETURN{}
  | \secd@CONST{〈Value〉}
  | \secd@PRIM{〈PrimitiveCommand〉}

de Bruijnインデックスはその個数だけ * を並べるという一進法で表しています：

〈Index〉 ::= ［*］

まあde Bruijnインデックスは動的には増えないしプログラムの大きさ程度にしかならないので1進法でも別にいいという感じではありますが，実は定数である自然数もその個数だけ o を並べるという一進法でエンコードされています：

〈Number〉 ::= ［o］

〈Bool〉 ::= T | F

要するに計算途中に5億とか出たら o が5億個並ぶ内部表現になります．全然スケールせずやばい．二進法に修正することも可能なはずですが，実は最終結果をPDFに十進法で印字することを目指した都合で「とりあえず一進法なら実装が楽そうだな」と思いひとまずこういう形式化になっています．もし本気でこのソフトウェアを発達させるなら二進法の内部表現に切り替えたいですが，本気で発達させる気が今後起きる気はあまりしません．

多少技巧的なところ

今回の実装で技巧的な箇所があるとすれば以下の2つです（かなりTeX言語に詳しい方向けの端折った解説になっています）：

`\expandafter` と `\romannumeral` トリックによる先頭完全展開の促進

$\mathrm{Access}(i)$ に対する処理でインデックス $i$ を使って環境 $E$ から値を取り出す処理や，加算などのプリミティヴによる計算を行なってその計算結果をスタックに積み直す処理など，いくつかの箇所で \romannumeral による先頭完全展開をふんだんに利用しています．

`\hop` トリック

これは伏線としてアドベントカレンダーで先週紹介しましたが，\romannumeral トリックによる先頭完全展開可能にするために \hop トリックを多用しています．

TeX言語の条件分岐の展開規則と \hop トリック＋応用 - Qiita

制御綴としては実装中の \secd@Hop，\secd@Then，\secd@HopOr がそれに相当します．実は \hop トリック以外にも条件分岐を早期脱出する手法はあるのですが，\hop トリックは \ifcase によって3つ以上の条件分岐がある状況でも簡単に拡張できるのが利点だな，と書いていて感じました．

まとめ

かなり雑然とした紹介になりましたが，型なしλ計算が完全展開可能な形で値呼びで評価できることを示しました．今回の記事では階乗の具体例で登場するだけで解説していませんが，（値呼びだと言語機能として追加しなけれなならない）条件分岐も扱うことができています．

現時点では特に実用性があるわけではありませんが，完全展開に限定してもTeX言語はTuring完全性をもつことを簡潔に示せたということが意義としてはあるかなという気がします．

もしもっと実用的なものにするなら，型なしλ計算で実装した処理をTeX/LaTeX側から呼べるようにするFFIの仕組みを導入してもいいかもしれません．

想定される質問：完全展開可能で嬉しいことあるか？
- 回答：わからん．まあ実装できたことは嬉しい
想定される質問：そういえばコンパイラ自体はTeX言語で書かなかったの？
- 回答：それをやるには人生が惜しいのでやめました
想定される質問：こんなソフトウェアを書いた時点で既に時間を無駄にしていないか？
- 回答：はい

OCamlユーザにとっては言わずもがなですが，名前は js_of_ocaml が元ネタです．この js_of_ocaml もさらに string_of_int などの標準ライブラリの特徴的な函数名を元ネタとしてつけられたと思しき名前ではあります． ↩
主にRustを学習する機会にちょうどいいやと思い簡単に書いたものです．コードはあまり洗煉されていません． ↩
Peter J. Landin. The Mechanical Evaluation of Expression. Computer Journal, 6, pp.308–320. 1964. ↩
ただし最終結果がクロージャの場合は単に (closure) と印字されます．OCamlのREPLで函数が計算結果だった場合に <fun> と標準出力に出るようなものです． ↩
なお，コード中の fix は 不動点コンビネータ と呼ばれる機構で，ここでは型なしの言語設定のため言語機能として用意せずとも定義できます（型つきの言語だと言語機能として入れないと使えません）． ↩
これはTeX言語の展開や実行の仕組みをほぼ知らない方向けに説明することが限りなく難しいですが，トークンには展開できるものとできないものの区別があり，展開できないものは通常の文字や一部プリミティヴが該当します．完全展開の文脈で展開できないトークンに出会った場合は単なる文字のように “出力の一部になるもの” としてその場では読み飛ばされます．展開できないトークンが消えたり，それに出会うとエラーになったりするわけではありません． ↩
実際には言語機能に応じてインストラクションの種類がいろいろ増えたりします． ↩
勿論0以上の整数のことです． ↩