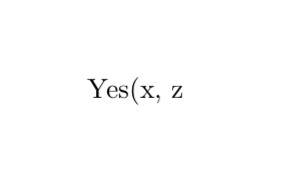TeX言語の条件分岐の展開規則と \hop トリック ＋応用

※この記事は背景知識の説明がそこそこ不親切です．多少TeX言語プログラミングで展開制御を経験している方向けです（そんな人日本語が読める人のうちでは数百人くらいしかいないんじゃないか？）．

概要

TeX言語に於ける条件分岐の処理は，そのままで使うには複雑な展開制御とやや相性の悪い定式化が為されています．展開制御中に見通しよく条件分岐を行なう方法として TeX by Topic¹ で紹介されている \hop トリックと呼ばれる技法が知られており，これを紹介します．またこの \hop トリックはelse節のみに使えるものでしたが，then節版も簡単に作れるので，それも紹介します．

条件分岐を展開する際の意味論

TeX言語には \if や \ifx をはじめとして種々の条件分岐があります（ここでは逐一紹介しませんが，The TeXbook² や TeX by Topic¹ で網羅的に触れられています）．どんな条件分岐かはここでは特に重要ではないので以降では \ifx を使うことにします．

\ifx はご存知のとおり通常以下のような形で使用します：

\ifx〈T1: token〉〈T2: token〉〈P1: tokens〉\else〈P2: tokens〉\fi

この記述が大雑把に言えば「〈T1〉 と 〈T2〉 が “\ifx の意味で等しい” 場合はthen節に相当する 〈P1〉 が，“等しくない” 場合はelse節に相当する 〈P2〉 がそれぞれ選ばれる」という機能を有することもよくご存知かと思います．

ただ，この記述がどのように展開されるかは案外非自明です．最初に 〈T1〉 と 〈T2〉 が等しいか否かを判定するまではまあ良いとして（\ifnum など数字列が条件式中に現れうる場合は条件式の終端がどこなのかを探索するために複雑になりますが，それは終端を示す \relax を置くなどの簡単な回避方法がある ³ のでここでは触れないことにします），判定後の動作がやや特殊とも思える定式化をとっています．一般的なプログラミング言語とのアナロジーを考えると，展開は以下の例のように “ifの部分全体がスッパリとthen節かelse節のトークン列に置き換わる” ような規則で行なわれると思うかもしれません：

\ifx\cmdA\cmdB␣Yes\hoge{x}\else␣No\piyo{y}\fi{z}
    ↓ \cmdA と \cmdB は等しいと判定し，then節だけ取り出される
Yes\hoge{x}{z}
    ↓
Yes(x, z)

ただし，\hoge と \piyo は以下で定義されているとします（後者は使われないのでなんでも良いです）：

\def\hoge#1#2{(#1, #2)}
\def\piyo#1#2{PIYO}

しかし，実はこうはなりません．実際に以下の例を使って試してみましょう（かなりLaTeXとして行儀の悪い書き方ですが，簡単のため）：

\documentclass{jsarticle}
\makeatletter
  \def\hoge#1#2{(#1, #2)}
  \def\piyo#1#2{PIYO}
  \def\cmdA{\dummy}
  \def\cmdB{\dummy}
\makeatother
\begin{document}
  \ifx\cmdA\cmdB Yes\hoge{x}\else No\piyo{y}\fi{z}
\end{document}

これを処理すると次のような結果になります：

なんと閉じ括弧が消えます！（どうしてこんなことに？ そんなところだけヘンテコになることあるか？）と思うかもしれませんが，これは次節のように説明がつきます．

（おそらく）実際の展開規則

特にこの展開規則について正確に記述した文献も知る限りありませんし，また処理系の実装を読んだわけでもありませんが，振舞いからするにおそらく以下のような規則で展開されているものと推測されます．まずは簡単のため最初の例とは少し違うトークン列を用います（▶ で現在の展開を開始する位置を，▷ でトークン化を開始する位置を，［ … ］ で既にトークン化された入力を示します）：

▶［\ifx］▷\cmdA\cmdB␣Yes\else␣No\fi!
    ↓ \ifx を読んだので次の2トークンを探す
▶［\ifx］［\cmdA］［\cmdB］▷Yes\else␣No\fi!
    ↓ \cmdA と \cmdB の等しさを定義を見て判定し，等しいとわかった．
      そこで現在の条件分岐の入れ子ではthen節を見るというフラグを入れ，条件式のトークン列は捨てる
     （フラグはスタックをなしており，条件分岐に入るたびにスタックにthenかelseのフラグが積まれる）
▶▷Yes\else␣No\fi!
    ↓ then節を普通にトークン化・展開し始める
［Y］［e］［s］▶［\else］▷No\fi!
    ↓ \else を読んだので，以降は \fi を見るまでトークン化しつつ読み捨てる
［Y］［e］［s］▶［\fi］▷!
    ↓ \fi を読んだので，\fi と条件分岐の現在の入れ子でのフラグを捨てる（スタックの頂上のフラグを捨てる）
［Y］［e］［s］▶▷!
    ↓ 以降は通常どおり
［Y］［e］［s］［!］▶▷

同様にelse節の場合は以下のように振舞うと推測されます：

▶［\ifx］▷\cmdA\cmdB␣Yes\else␣No\fi!
    ↓ \ifx を読んだので次の2トークンを探す
▶［\ifx］［\cmdA］［\cmdB］▷Yes\else␣No\fi!
    ↓ \cmdA と \cmdB の等しさを定義を見て判定し，等しくないとわかった．
      そこでelse節を見るというフラグをスタックに積み，条件式のトークン列を捨てる
▶▷Yes\else␣No\fi!
    ↓ \else か \fi を見るまでトークン化しつつ捨てる
▶［\else］▷No\fi!
    ↓ \else を読んだので，以降は \fi を見るまで通常どおり処理する
［N］［o］▶［\fi］▷!
    ↓ \fi を読んだので，\fi とスタックの頂上のフラグを捨てる
［N］［o］▶▷!
    ↓ 以降は通常どおり
［N］［o］［!］▶▷

さて，これをもとに当初の例に当てはめてみると次のようになります：

▶［\ifx］▷\cmdA\cmdB␣Yes\hoge{x}\else␣No\piyo{y}\fi{z}
    ↓ \ifx を読んだので次の2トークンを探す
▶［\ifx］［\cmdA］［\cmdB］▷Yes\hoge{x}\else␣No\piyo{y}\fi{z}
    ↓ \cmdA と \cmdB の等しさを定義を見て判定し，等しいとわかった．
      then節を見るというフラグをスタックにプッシュし，条件式のトークン列は捨てる
▶▷Yes\hoge{x}\else␣No\piyo{y}\fi{z}
    ↓ then節を普通にトークン化・展開し始める
［Y］［e］［s］▶［\hoge］▷{x}\else␣No\piyo{y}\fi{z}
    ↓ \hoge の定義に合致するまでトークン化する
［Y］［e］［s］▶［\hoge］［{］［x］［}］［\else］▷No\piyo{y}\fi{z}
    ↓ \hoge の定義に合致したので，定義に基づいて展開する
     （ここで \else を読んではいるが，それを展開する文脈で出会ったわけではないので以降を捨てたりはしない）
［Y］［e］［s］▶［(］［x］［,］［␣］［\else］［)］▷No\piyo{y}\fi{z}
    ↓ 展開不能なのでそのまま飛ばす
［Y］［e］［s］［(］［x］［,］［␣］▶［\else］［)］▷No\piyo{y}\fi{z}
    ↓ \else を読んだので，以降は \fi を見るまでトークン化しては捨てる
［Y］［e］［s］［(］［x］［,］［␣］▶［\fi］▷{z}
    ↓ \fi を読んだので，\fi とスタックの頂上のフラグを捨てる
［Y］［e］［s］［(］［x］［,］［␣］▶▷{z}
    ↓ 以降は通常どおり
［Y］［e］［s］［(］［x］［,］［␣］［{］［z］［}］▶▷

というわけでたしかに “閉じ括弧だけ消えた” 結果になるようなトークン列となりました（上記の処理を見れば「\hoge の定義中の #2 に \else がきてしまったことでそれより後ろが吹き飛んだ．z はたまたま後ろにくっついただけ」という様相です）．

なお，このような時系列的な振舞いは \tracingmacros=1\relax をこの展開を行なう手前の箇所に書いて処理しログファイルに出力される展開履歴を見ても観察できます．

条件分岐が展開制御で邪魔になる例

しかし，現実にはTeX言語プログラミングをしていると “スッパリthen節かelse節の一方の内容だけになる条件分岐” が欲しいときはあります．特に顕著なのは，\romannumeral トリック⁴ で先頭完全展開されて欲しいときに，通常の \ifx などを使うとthen節やelse節の中で展開不能なトークンが出てきて完全展開が終わり，そのまま \else … \fi や \fi が残ってしまったりする状況です．

例として自然数の前者函数 \predec を実装する状況を見てみましょう．自然数はその個数の o を並べることによって表現するとします（例によってとても行儀の悪いLaTeXコードです）：

\documentclass{jsarticle}
\makeatletter
%定義：
  \def\local@unique{\local@unique@inner}
  \def\predec#1{%
    \ifx\local@unique#1\local@unique
      % 空列のとき，すなわち 0 のときは，空列を返す
    \else
      % 正整数のときは 1 個削る
      \predec@positive#1\local@end
    \fi
  }
  \def\predec@positive o#1\local@end{#1}
%計算：
  % 4 - 1 = 3
  \edef\resultA{\predec{oooo}}
\makeatother
\begin{document}
  \resultA
\end{document}

これを実行するとたしかに「ooo」と表示され，$4 - 1$ が \edef による完全展開の下で計算できています．しかし，実はこの実装は完全展開可能ながら “函数として合成” することができません．試しに \resultA の下に以下のような定義を入れ，文書の本文を \resultA, \resultB に変えて処理してみましょう：

  % (4 - 1) - 1 = 2
  \edef\resultB{\expandafter\predec\expandafter{\romannumeral-`0\predec{oooo}}}

合成可能なら「ooo, oo」と出るはずですが，実際には次のようなエラーが出ます：

! Undefined control sequence.
\local@unique ->\local@unique@inner

l.17 ...expandafter{\romannumeral-`0\predec{oooo}}
                                                  }
No pages of output.

何が起こったのかは順を追えばわかります（\tracingmacros=1\relax でも様子を見ることができます）：

▶［\expandafter］▷\predec\expandafter{\romannumeral-`0\predec{oooo}}
    ↓ \expandafter を読んだので，次のトークンを読んで一時的に飛ばす
▶［\predec］▶▷\expandafter{\romannumeral-`0\predec{oooo}}
    ↓
▶［\predec］▶［\expandafter］▷{\romannumeral-`0\predec{oooo}}
    ↓ また \expandafter なので同様
▶［\predec］［{］▶▷\romannumeral-`0\predec{oooo}}
    ↓
▶［\predec］［{］▶［\romannumeral］▷-`0\predec{oooo}}
    ↓ \rommannumeral を読んだので，先頭完全展開を始める
▶［\predec］［{］▶［\romannumeral］［-］［`］［0］［\predec］▷{oooo}}
    ↓ \predec を読んだので，これの定義に合致するまでトークン化する
      （以降 ［\romannumeral］［-］［`］［0］ は R と書くことにする）
▶［\predec］［{］▶ R ［\predec］［{］［o］［o］［o］［o］［}］▷}
    ↓ 展開
▶［\predec］［{］▶ R ▶［\ifx］［\local@unique］［o］［o］［o］［o］［\local@unique］［\else］
    ［\local@predec@positive］［o］［o］［o］［o］［\local@end］［\fi］▷}
    ↓ 条件式の2トークンは \ifx の意味で等しくないので，
      else節を見るというフラグをスタックに積んで \else か \fi まで読み捨てる
▶［\predec］［{］▶ R ▶［\local@predec@positive］［o］［o］［o］［o］［\local@end］［\fi］▷}
    ↓ 定義に基づいて展開
▶［\predec］［{］▶ R ▶［o］［o］［o］［\fi］▷}
    ↓ 展開できないトークンに出くわしたので，ここで先頭完全展開が終わる．
      0 以下の数になったので \romannumeral の結果は空列になる．
      \expandafter で生じていた一時的な ▶ は消え，本来の展開開始位置に戻る．
      **このとき，\fi は消えずに残る！**
▶［\predec］［{］［o］［o］［o］［\fi］▷}
    ↓ \predec の定義に合致するまでトークン化
▶［\predec］［{］［o］［o］［o］［\fi］［}］▷
    ↓ 展開
▶［\ifx］［\local@unique］［o］［o］［o］［\fi］［\local@unique］［\else］（中略）［\fi］［}］▷
    ↓ \ifx の意味で等しくないので，else節を見るというフラグをスタックに積んで \else か \fi まで読み捨てる
▶［\fi］［\local@unique］［\else］（中略）［\fi］［}］▷
    ↓ **残ってしまった \fi が終端だと思われてしまう！** フラグをひとつスタック頂上から取り除く
▶［\local@unique］［\else］（中略）［\fi］［}］
    ↓ 展開
▶［\local@unique@inner］［\else］（中略）［\fi］［}］
未定義でエラー

\fi が残るために，こういうかなり厄介なことが起こっていたのです．いずれにせよ，こうした状況でも機能する条件分岐を実現したいというモティヴェーションがあるわけです．

\hop トリック

実は \hop トリックと呼ばれる簡単な解決方法が知られています¹（ただし，後述しますが少しだけ注意が必要です）．まず，以下で \hop を定義します（勿論，名前は \hop でなくても構いません）：

\def\hop#1\fi{\fi#1}

そしてこの \hop を \else の直後に置きます．これだけでうまい具合に “else節内の展開が始まる前に条件分岐を脱出できる” のです．

では，前節の例にこの \hop トリックを適用してみましょう．\hop の定義を追加し，\else の後ろに追記します：

\documentclass{jsarticle}
\makeatletter
%定義：
  \def\hop#1\fi{\fi#1}
  \def\local@unique{\local@unique@inner}
  \def\predec#1{%
    \ifx\local@unique#1\local@unique
      % 0 に対しては 0 として空列を返す
    \else\hop
      % 正整数に対しては 1 個削る
      \predec@positive#1\local@end
    \fi
  }
  \def\predec@positive o#1\local@end{#1}
%計算：
  % 4 - 1 = 3
  \edef\resultA{\predec{oooo}}
  % (4 - 1) - 1 = 2
  \edef\resultB{\expandafter\predec\expandafter{\romannumeral-`0\predec{oooo}}}
\makeatother
\begin{document}
  \resultA, \resultB
\end{document}

これで処理すると文書生成に成功し，たしかに「ooo, oo」と印字されています．めでたし．

“うまい具合にelse節が条件分岐の外に押し出され，else節が展開されるより先に条件分岐を脱出する” 様子を具体的に追ってみます：

▶［\predec］［{］ R ▶［\ifx］［\local@unique］［o］［o］［o］［o］［\local@unique］［\else］
    ［\hop］［\local@predec@positive］［o］［o］［o］［o］［\local@end］［\fi］▷}
    ↓ 条件式の2トークンは \ifx の意味で等しくないので，else節を見るというフラグをスタックに積んで \else か \fi まで読み捨てる
▶［\predec］［{］ R ▶［\hop］［\local@predec@positive］［o］［o］［o］［o］［\local@end］［\fi］▷}
    ↓ **\hop の定義に基づいて展開**
▶［\predec］［{］ R ▶［\fi］［\local@predec@positive］［o］［o］［o］［o］［\local@end］▷}
    ↓ **\fi を読んだので，スタック頂上からフラグを捨てる**
▶［\predec］［{］ R ▶［\local@predec@positive］［o］［o］［o］［o］［\local@end］▷}
    ↓ 展開
▶［\predec］［{］ R ▶［o］［o］［o］▷}
    ↓ 展開できないトークンに出くわしたので，ここで先頭完全展開が終わる．
      0 以下の数だったので \romannumeral の結果は空列になる．
      \expandafter で生じていた一時的な ▶ は消え，本来の展開開始位置に戻る．
▶［\predec］［{］［o］［o］［o］▷}
    ↓ \predec の定義に合致するまでトークン化
▶［\predec］［{］［o］［o］［o］［}］▷
    ↓ 展開
▶［\ifx］［\local@unique］［o］［o］［o］［\local@unique］［\else］
    ［\hop］［\local@predec@positive］［o］［o］［o］［\local@end］［\fi］▷
    ↓ \ifx の意味で等しくないので，else節を見るというフラグをスタックに積んで \else か \fi まで読み捨てる
▶［\hop］［\local@predec@positive］［o］［o］［o］［\local@end］［\fi］▷
    ↓ **\hop の定義に基づいて展開**
▶［\fi］［\local@predec@positive］［o］［o］［o］［\local@end］▷
    ↓ **\fi を読んだので，スタック頂上からフラグを捨てる**
▶［\local@predec@positive］［o］［o］［o］［\local@end］▷
    ↓ 展開
［o］［o］

というわけでうまくいっていることがわかります．

ただしこれは万能ではなく，注意点があります．勘の良い方はお気づきかもしれませんが，陽に書かれた入れ子の条件分岐には対応していません．すなわち，例えば以下のような使い方はできません：

%% 1トークン受け取り，それが a か b かそれ以外かを印字するコマンド
\def\check#1{
  \ifx a#1%
    A%
  \else\hop
    \ifx b#1%
      B%
    \else\hop
      Other%
    \fi
  \fi
}

これだと2つ \fi がトークン列に出現し，外側の \hop を展開する際に手前側の意図しない \fi が使われてしまいます．したがって，入れ子の条件分岐を書きたい場合は定義を分ける必要があります：

%% 1トークン受け取り，それが a か b かそれ以外かを印字するコマンド
\def\check#1{
  \ifx a#1%
    A%
  \else\hop
    \checkSub{#1}%
  \fi
}
\def\checkSub#1{%
  \ifx b#1%
    B%
  \else\hop
    Other%
  \fi
}

\hop トリックをthen節に拡張する

前節の \hop トリックはelse節にしか適用できないものでしたが，then節にも同様のトリックが欲しいはずです．実際，上で例に挙げた \predec で 0 の場合に対応する必要がなかったのはたまたま “戻り値” が空列で，後続する \else も先頭完全展開によって展開されたからでしかありません．もし 0 の場合だけ例えば z という表現をするように変えたければ，then節にも \hop トリックめいたことをやらねばならないはずです．

で，その \hop トリックのthen節版も簡単にできるなと思ったので紹介します．

以下で定義される \then を条件式の直後に置くとよいです：

\def\then#1\else#2\fi{\fi#1}

動作原理は \hop と全く同様です．ここまで読んでくださった方なら（ああ，これはたしかに動きそうだな）と感じられるかと思います．ちなみに，特に意味はありませんが以下の定義でも動きます（一方で \hop の場合は \else を加えると当然ながら動きません）：

\def\then#1\else#2\fi{\else\fi#1}

\hop と同様に，こちらの \then も陽に入れ子になった条件分岐には対応できないので注意してください．

まとめ

本記事では，TeX言語の条件分岐プリミティヴが非自明な展開規則をもち，しばしば（特に先頭完全展開の文脈に於いて顕著に）“意図した展開と整合しない” という落とし穴があることを前提として紹介し，その解決方法としてelse節に対する \hop トリックが知られていること，またそれを応用してthen節に対する “\then トリック” も実現できることを解説しました．

蛇足

ちなみに，もし仮に条件分岐が “スッパリthen節だけかelse節だけになる ”ような展開規則だとすると，展開とトークン化は同時進行なので \fi を見つけるまで先読みしてトークン化しなければならないはずで，したがって以下のような処理になるはずです：

▶［\ifx］▷\cmdA\cmdB␣Yes\hoge\else␣No\piyo\fi{x}
    ↓ \ifx を読んだので次の2トークンを探す
▶［\ifx］［\cmdA］［\cmdB］▷Yes\hoge\else␣No\piyo\fi{x}
    ↓ \cmdA と \cmdB が等しいとわかった．そこでthen節だけを残すべく \fi を見つけるまでトークン化する
▶［\ifx］［\cmdA］［\cmdB］［Y］［e］［s］［\hoge］［\else］［N］［o］［\piyo］［\fi］▷{x}
    ↓ \else と \fi を読んだので，then節にあったトークンだけ残す
▶［Y］［e］［s］［\hoge］▷{x}
    ↓ 展開不能なトークンなので読み進める
［Y］［e］［s］▶［\hoge］▷{x}
    ↓ \hoge の定義に合致するところまでトークン化する
［Y］［e］［s］▶［\hoge］［{］［x］［}］▷
    ↓
［Y］［e］［s］▶［(］［x］［,］［␣］［z］［)］▷

要するに \fi を見つけるまでトークン化を一気に行なわないことには成り立たない規則です．勿論こういう規則として定式化してもよかったかもしれませんが，実際のTeX言語の展開規則はこうはなっていないということです．どうしてこうした規則を採用しなかったのか正確な意図は知りませんが，おそらくはthen節内やelse節内でカテゴリーコードを弄ったりしたいという都合があり，それゆえ “展開せずトークン化だけどんどん進める” ような展開規則にはしたくなかったのかもしれません（もし上記のような規則だと，then節内やelse節内でのカテゴリーコード変更は \fi よりも後方でしか反映されなくなってしまうため）．

1. Victor Eijkhout. TeX by Topic. Addison–Wesley, 1991. ↩ ↩² ↩³

2. Donald. E. Knuth. The TeXbook. Addison–Wisley, 1986. ↩

3. @wtsnjp. \relax の使い方 12連発 - 0番染色体. 2015. ↩

4. @zr_tex8r. \romannumeral の基本的な使い方（“関数”の合成） - マクロツイーター. 2015. ↩