はじめに
皆さんはモデルベース開発(MBD)という言葉を知っているでしょうか?
MBDは設計プロセスの1手法であり、その名の通りモデルを使った開発ワークフローの総称となります。
MBDといえば下図のV字ワークフローで示されることが代表的です。
(各フェーズでの工程の定義は人によってまちまちです)

左のVが設計の上流工程となっており、右が下流工程を表しています。
まず最上流の工程にて設計の要件や仕様を定義していきます。
システムアーキテクチャーを設計してシステムのインターフェイスを固めていく、いわゆるシステムズエンジニアリングを行う場合もここに含まれます。
要件がある程度固まった後に実際に制御系のモデル作成やプラントモデリングを行って、モデルを使った机上シミュレーション(MILS : Model Loop In the Simulation)を繰り返していきます。
その際にはモデルの安全性の検証作業として、テストシナリオでの評価やカバレッジ分析なども行ったりします。
また設計の段階で実機を用いたコンセプト検証を行うラピッドプロトタイピング(RCP : Rapid Control Prototyping)を実施する場合もあります。
RCPでは、SpeedgoatのようなリアルタイムOS(RTOS)搭載のターゲットにコントローラーのモデルを自動コード生成して実装し、実機の制御対象を制御するというものです。
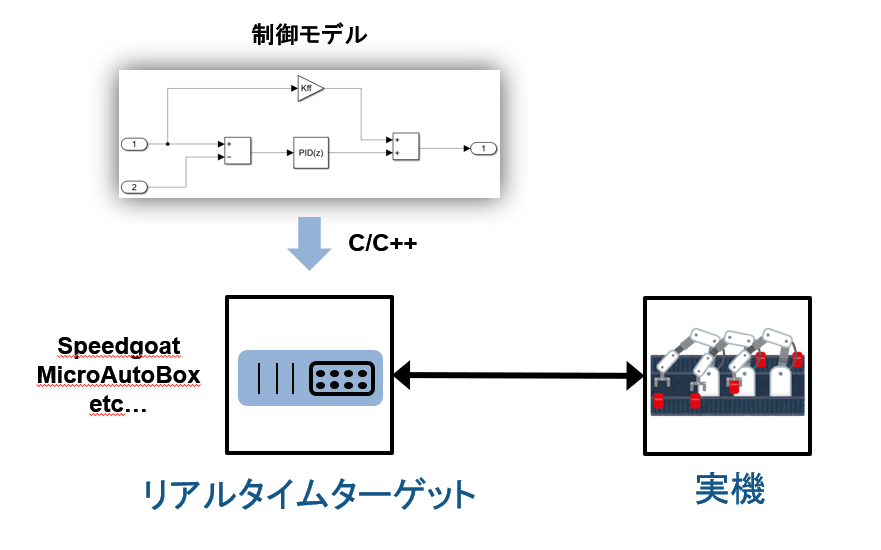
制御系設計の早い段階で実機検証が行えるため、性能の評価や複数の制御アルゴの検討などを行うことができます。
基本設計が完了した後、インターロック等を盛り込んだより詳細な制御ソフトウェア用のコントローラーモデル開発を行い、また同様にテストのループを繰り返します。
そうして、確認されたコントローラーモデルから自動コード生成(PCG : Product Code Generation)を行います。
コード生成を行う機能としては、MATLAB製品ファミリーであるMATLAB Coder™、Simulink Coder™、Embedded Coder®の機能が利用できます。
!Coder機能の違い!
MATLAB Coder™ :
MATLABコードからのC/C++コード生成
Simulink Coder™:
モデルからのC/C++コード生成、RCP/HILやシミュレーションのアクセラレータ用途が主(要MATLAB Coder™)
Embedded Coder®:
MATLAB Coder™、Simulink Coder™の強化機能、組み込みシステム用にコードを最適化するオプションを提供(要MATLAB Coder™、Simulink Coder™)
コード生成のフェーズを通過すると、V字の右側に行きます。
下流ではモデルと生成コードとの等価性検証、いわゆるBack to Back検証や生成コード上におけるランタイムエラーといった致命的な欠陥がないことを確認する静的、動的なテスト検証を行います。
この際、コントローラーのモデルをコード生成してシミュレーションを行うSILS : Software In the Loop Simulationやコード生成した結果を実際のマイコンなどのターゲット上に実装してシミュレーションするPILS : Processor In the Loop Simulationを行うこともあります。
PILSはターゲット上でコントローラーが動きますのでリアルタイム性の計測に用いることができます。
検証が終了した後は、結合試験としてコントローラーのソフトウェアを統合した動作検証を行います。
その際には、制御を実際のターゲット(マイコンなど)に実装し、制御対象であるプラントモデルをコード生成してSpeedgoatなどのリアルタイムターゲットに実装し試験する、いわゆるHILS : Hardware In the Loop Simulationを行うこともあります。
HILSはプラントモデルがリアルタイムに動作するという点と、故障ケースなど実機では簡単に試せない様々なテスト検証を行う目的があります。
結合試験が完了したあとは、実際に実機での評価、量産展開に向けた適合となります。
以上のようにMBDの根幹にあるのは、モデルです。
モデルを使って洗練した設計を行うことで、後戻りによる余計な工数の削減や設計そのもののパフォーマンス向上を図ることを狙いとしています。
MBDのワークフローを意識して制御設計を行う
では、実際にMBDを意識して設計を行ってみます。
今回題材とするのは、High Power Gearboxによるアーム回転角の制御です。

こちらはTechShare社から販売されている以下の教材で紹介されているものになります。
ArduinoとMATLABで制御系設計をはじめよう! [ISBN-M-978-4906864003]
ArduinoとMATLABで制御系設計をはじめよう!実験キット [TSI-S001]
使用機材としては以下の通り。
なお、↑のキットを購入するとマイコン以外全部ついてきます。
(詳細は販売先の情報を確認してください)
| 使用機材 |
|---|
| High Power Gearbox H.E. |
| ユニバーサルプレート |
| ポテンショメータ取り付け専用プレート |
| ポテンショメータ |
| モータードライバーIC 東芝製TA7291P |
| NUCLEO-H743ZI2 |
教材と違うのは、ArduinoではなくSTMicroelectronicsのNucleoボードを使用している点のみです。
MATLAB/SimulinkではArduinoはもちろんのこと、Nucleoなど特定のボード向けに無償のハードウェアサポートパッケージというものが提供されています。
ハードウェアサポートパッケージはマイコン搭載のペリフェラル(周辺機能)を叩くためのブロックやマイコンへの実装、PILS、実行などを支援してくれる機能が提供されており、基本コーディングレスでソフトをモデルから生成できます。
なお、コード生成を伴うので必要に応じてSimulink Coder™などの製品が必要となるものがありますので事前にサポートパッケージの製品情報を確認してください。
Arduino Support from Simulink
STMicroelectronics Hardware Support from Simulink
!重要!
サポートパッケージがないボードは、Coder製品によるモデルからのC/C++コード生成を行った後は、デバイスドライバーなどのペリフェラルの外部ソース結合やmain.c作成、マイコンへの割り込みハンドラの登録など含むソフト作成を外部の統合環境(IDE)にて自前で行う必要があります。要するに、Simulinkモデルは制御のアプリ部分のコードが出ているのみになるので、残りはコーディングし、ビルド及びターゲット展開まで自前で行います。
制御系設計から実装までの流れ
まず目指すべき設計の要求仕様は以下の通りです。
・High Power Gearboxのアーム回転角を±90[deg]の範囲でサーボ制御する
・コントローラーはセンサ(ポテンショメーター)から回転角(電圧)で受け取り、degに変換してフィードバック制御する
・コントローラーはアームの目標回転角とセンサからの実測値を比較して、制御偏差を小さくするように適切なPWM出力を計算する
システムアーキテクチャー図(System Composer™利用)を構成すると以下のイメージです。

ナンチャッテな要求仕様の策定ができたので、コントローラー開発を以下の流れに沿ってやっていきたいと思います。

①~④が基本設計、⑤でコード生成及びPILSによる検証といって実機試験と進めていくことにします。
なお、使用するMATLABはR2021bです。
①実験データの取得
今回は実験データの取得にもSimulinkモデルを利用したいと思います。
先に紹介したSimulink Coder Support for STMicroelectronics Nucleo BoardsというサポートパッケージをMATLABのAdd-onからインストールすると、Simulinkのライブラリブラウザにライブラリのブロックが登録されます。
ライブラリには、アナログIO、デジタルIO、PWMなどペリフェラルのブロックなどが登録されています。
実験用にコード生成して利用するモデルは下図の通りです。

(NUCLEO-H743ZI2の基準電圧としてVref=5[V]としています)
実験ではNUCLEO-H743ZI2のアナログ入力ピンA0からアームに取り付けているポテンショメータの電圧値(0-1で正規化されてAnalog IOブロックから入力される)を読み取って、それを対応する角度[deg]にモデル上で変換し、これを出力データとします。
またアーム回転角と出力電圧の関係は事前にラフに計測して、一次関数としてフィッティングを行っています。
アーム回転角と電圧値の関係
| 角度[deg] | 電圧[V] |
|---|---|
| -90 | 0 |
| 0 | 2.5 |
| 90 | 5 |
入力データは振幅3[V]、周期1秒、パルス幅50%の矩形波入力として、これをPWM[%]に変換してボードのPWM対応ピンから出力し、モーターを駆動します。
実験を行う前に、まずNucleoボードのドライバーのインストールとしてSetupを済ましておきます。
その後、モデルのコンフィギュレーション設定>ハードウェア実行にてハードウェアボードの種類とハードウェアボード設定にてCOMポートの設定を行います。
(ボードとはUSBケーブルをつないでホストPCとの間でシリアル通信を行いますので、PCのデバイスマネージャーでCOMポートの確認をしておきます)

以上でモデルをコード生成して、ボードに実装して動かす準備が整いました。
あとは、Simulinkモデル上でモードをボード上で実行として、監視と調整ボタンを押すとコード生成~実験が開始されます。

なお、監視と調整はSimulinkのエクスターナルモードと呼ばれる実行方法の一つで、ターゲット上に実装したスタンドロンのコントローラーとMATLABのSimulinkモデルにおいて対応する信号の監視やロギングのほか、Gainなど調整可能な変数のオンライン変更を行うことができます。
これで実験を行って、システム同定に使う実験データをMATLAB上で取得できます。
以下は実験の様子を収めたGIFアニメーションです。
取得した実験データは以下の通りです。
②プラントモデルの同定
このデータを使ってプラントモデルを構築していきます。
プラントモデルの構築には3種類あります。
1.ホワイトボックスモデリング:
原理式からプラントやパラメーターを構築する
2.ブラックボックスモデリング:
モデルを完全な未知として扱ってデータからすべてを推定する
3.グレーボックスモデリング:
ホワイトとブラックの中間のモデリング、式やモデルの一部分が未知のためデータなどから推定する
今回対象とする制御対象はDCモーター及びギアが支配的な要素であり、原理式から立式すると、最終的に入力からアーム角速度までは一次遅れ(時定数+ゲイン)で簡略化することができます。
よって、一次遅れの時定数とゲインをデータから求める3のグレーボックスモデリングを行います。
なお、2のブラックボックスモデリングを行う場合にはMATLABの製品であるSystem Identification Toolbox™によって行うことができます。
さて、グレーボックスモデリングを行うにあたり、まずは下図の通りSimulinkモデルを用意します。

一次遅れ+積分器でモーター入力~アーム回転角までのプラントを表現し、その出力でradからdeg変換しています。
またプラント入力は実験で用いたものと同じです。
時定数TとゲインKをデータからフィッティングを掛けます。
この際にMATLABの製品であるSimulink Design Optimization™(以降、SDOで省略)を利用したいと思います。
SDOはモデルのパラメーター最適化やモンテカルロシミュレーションに基づく感度解析機能を提供している製品です。
プラントモデリングから制御系設計、感度評価まで実用上幅広く利用することが可能です。
今回のタスクであるグレーボックスモデリングを行う機能として、SDOのパラメーター推定器というアプリを利用します。
パラメーター推定器は実験データとモデルのパラメーターフィッティングをサポートしてくれる機能で、Simulinkモデルのアプリからアイコンをクリックして起動できます。

アプリが起動したら新しい実験をクリックして、データに対応するモデル上のライン選択及びデータ(時系列)の対応付けを行います。
また、パラメーターの選択をクリックして、モデルで使用されている変数から調整を行うものを抽出します。

データはアーム回転角[deg]のデータ、調整する変数はK、T(初期値はどちらも1とする)としてフィッティングを実施します。
計算を始めるには、推定という再生ボタンをクリックします。
パラメーター推定器は最適化手法(要Optimization Toolbox™、推奨Global Optimization Toolbox)に基づいて、シミュレーションを反復しながら計算を行っていきます。
最終的に収束解が得られると計算がストップし、パラメーターが更新されます。

| パラメーター | 値 |
|---|---|
| 時定数T | 0.1399 |
| ゲインK | 1.3685 |
上図及び表が最終的な結果です。
どうやらモデルでは考慮していない要素(おそらくガタや摩擦)によって多少応答に差異が残っていますが、概ね良好な推定結果になっていると判断します。
なお、今回は省略しますが、学習に使用したデータ以外のデータを複数取っておいてモデルの検証(バリデーション)を行うことが大切です。
検証を行う理由は得られた結果が学習データに過適合、いわゆるオーバーフィッティングしていないかを確かめるためです。
パラメーター推定器では検証を行う機能も含まれています。
③コントローラー開発(制御系設計)
得られたプラントモデルをベースに制御系を設計していきます。
今回はModel Predictive Control Toolbox™を使ってモデル予測制御:MPCのコントローラーを設計します。
MPCについては過去の記事でも紹介しているので良ければどうぞ。
モデル予測制御を使ってロケットを垂直着陸させてみた
PID制御を極めよう ~原理から調整まで~(MPCも少し)
今回同定したモデルでは、モデル化していない要素の影響によってモデル化誤差が見込まれます。
そのため、制御にオフセットが発生する可能性が懸念されるため、MPCの予測モデルとしてプラントの状態量に積分器を追加した拡大系、いわゆるサーボ系を構成し対処することを考えます。
なお、Toolboxで提供されている線形なMPCのコントローラーには、デフォルトでオフセットフリー機構が入っています。
原理は、出力に未知な外乱が重畳されると仮定して、出力外乱モデルを状態量に含めて、拡大系を推定&制御するというアプローチです。
考え方は以下の論文が参考になります。
Combined Design of Disturbance Model and Observer for Offset-Free Model Predictive Control
ただし、今回は調整のし易さを考慮して、オフセットフリーの機構を殺して、外側から積分器で補償するアプローチをとります。
まずは予測モデル(拡大系)を構成して、MPCオブジェクトを設計します。
MPCは線形モデル予測制御で構成し、主なパラメーターは以下の通りとします。
| パラメーター | 値 |
|---|---|
| 制御周期 | 10[ms] |
| 予測ホライズン | 40 |
| 制御ホライズン | 2 |
| 操作量MVの上下限 | ±5[V] |
| 出力OVの重み(積分器, 出力) | (40, 20) |
評価関数
MPCの調整のポイントですが、予測ホライズンはプラントの過渡応答をカバーするように設定することが良いとされています。
今回同定によって得られたプラントの時定数Tは約0.1[s]なのでそれをカバーする0.4[s] (=制御周期0.01[s]×予測ホライズン40)としています。
制御ホライズンはMPCの設計変数の数に対応するので、あまり大きくすると計算負荷が上がります。一般には、2~4の間が良いようです。
出力の重みについては、積分器の状態、すなわち誤差の積算量を小さくすることに比重を置いて、回転角の2倍大きく設定しています。
ただし、積分制御のみだと回転角が目標値に対してオーバーシュートしやすくなるので、適度にレギュレーター制御を狙いたい意図で回転角の重みもある程度設けている形になります。
なお、MPCの調整Tipsについては、以下の情報が参考になります。
Toolbox開発者の一人であり、MPCの研究で世界的に著名なAlberto Bemporad教授のインタビュー動画:
How to Design Model Predictive Controllers
ペーパー資料:
モデル予測制御(MPC) 実時間最適制御により制御系のさらなる高性能化を目指す
MPCの設計スクリプトは次の通りです。
最後の行で組込みのオフセットフリー機構を殺しています。
% Grey box model
Ki = 2; % Integral gain
A = [0 1;0 -1/T];
B = [0;K/T];
C = [180/pi 0];
D = 0;
Aa = [0 Ki*C;zeros(2,1) A];
Ba = [0 -Ki;B zeros(2,1)];
Ca = [1 zeros(1,2);0 C];
Da = zeros(2,2);
sys = ss(A,B,C,D);
sysa = ss(Aa,Ba,Ca,Da);
sysa.InputName = {'volt','theta_ref'};
sya.OutputName = {'err','theta'};
sysa.InputGroup.MV = 1; % Manipulated Variable
sysa.InputGroup.MD = 2; % Measured Disturbance Input
% MPC Design
ts = 1e-2;
mpcobj = mpc(sysa,ts);
mpcobj.PredictionHorizon = 40;
mpcobj.ControlHorizon = 2;
mpcobj.ManipulatedVariables(1).Max = 5;
mpcobj.ManipulatedVariables(1).Min = -5;
mpcobj.Weights.OutputVariables = [40 20];
mpcobj.Weights.ManipulatedVariables = 0.1;
mpcobj.OutputVariables(1).ScaleFactor = 40;
mpcobj.OutputVariables(2).ScaleFactor = 40;
mpcobj.ManipulatedVariables.ScaleFactor = 5;
setoutdist(mpcobj,'model',tf(zeros(2,1))) % Disabling default offset-Free mechanism
④MILS検討
設計したコントローラーモデル及びMILS環境は下図の通りです。
コントローラーのモデルは単独のモデルとして作成し、モデル参照(Model Reference)という機能を利用してMILS用の統合モデルに呼んでいます。
シミュレーションのシナリオとして、アームの目標回転角±40[deg]を与えるのに加え、50[s]経過した時点で単位ステップの入力外乱を加えます。
下図はシミュレーション結果で、上段がアーム回転角、下段がMPCで計算した操作量です。
結果から分かるように、回転角は多少オーバーシュートしつつも目標角に追従しています。
また50[s]で外乱が発生しますが、すぐに影響を抑制していることが伺えます。
一方、操作量は制約値である±5[V]の範囲内で動作していることが分かります。
以上からMPCによる制御によって、良好な目標値追従性ならびに外乱抑制性を確保していることが確認できたとします。
⑤PILS検証
MILSの評価が完了したので、次はコントローラーのモデルをコード生成して、ターゲットボード上に実装した上でシミュレーションを行います。
PILSでは、制御はターゲットで計算して、プラントはPCのSimulinkモデルで計算します。

PILSによるBack to Back検証をサポートする機能がEmbedded Coder™から提供されています。
それがSIL/PILマネージャーです。
Simulinkモデルのツールストリップのアプリからアイコンをクリックすると起動します。
SIL/PILマネージャーではモデル参照を含むトップ階層のモデルにおいて、テスト対象のモデル参照をSILまたはPIL実行し、Back to Backの検証を自動化してくれる機能となっています。
今回は、MPCで設計したコントローラーモデルのモデル参照ブロックにおいてシミュレーションモードをプロセッサインザループに設定し、自動検証を行います。
検証が終了すると[実行の比較]アイコンから結果を確認できます。

上図はSimulinkのシミュレータデータインスペクター(SDI)という可視化機能の差分比較結果の様子であり、MILSとPILS実行の等価性を示しています。
×の場合には差分があることをレポートしているので、実際に誤差がどれだけあるのかをトレンドから確認します。
結果からみると浮動小数点誤差のオーダーで非常に小さい差分であるので許容範囲と判断することができます。
なお、MATLABの検証ツールであるSimulink Test™を用いるとBack 2 Back検証や期待値検証などのテスト管理及び実行をサポートしてくれます。
またSIL/PILマネージャーからSimulink Test™のテスト管理機能のテンプレートを吐き出すことも可能です。
さらにコンフィギュレーション設定において実行時間計測を行うことができるので、実際にMPCの計算にリアルタイム性があるのかを実行後に評価できます。

上図の2.Profiled Sections of Codeにて生成コードの各セクションにおいて実行に要した時間(最大、平均etc)を示しています。
この中で、mpcController[0.01 0]が実行本体であるループ中で制御周期10[ms]で呼ばれる制御ルーチンとなります。
上図は横軸がシミュレーション時間、縦軸が毎周期で要した時間を示しています。
図から10[ms]よりも十分に短い時間で計算が完了しているのでリアルタイム性があることを確認できます。
⑥実機試験
PILS検証も問題ないことを確認できたので、最後に実機を用いた試験を行います。
実行手順は①のデータ取得で紹介したエクスターナルモードの方法です。
手順は同じで異なるのはコード生成の対象がMPCのコントローラーモデルとなります。
実験では2つのパターンで評価を行います。
①無負荷での制御
②負荷がある場合の制御
②の負荷ありでは、アームに重り(30g)をつないだ状態で目標回転角に追従するかを評価します。
上図は2パターンの実験結果です。
アーム回転角の結果を見ると、MILSで確認されたオーバーシュートの傾向が出ていますが、良好に目標値に追従していることが確認できます。
特に重りをつけたことによる追従性の劣化は少なく、ロバストに制御できています。
またMPCで計算された操作量(入力)は指定した上下限±5[V]の範囲で計算されています。
最後のQP StatusはMPCで解かれたQP(2次計画問題)のステータスを表示しています。
これは、任意の正の値が出ていれば、その反復回数で最適解を見つけられたことを示しています。
結果から、概ね1-2回の反復で最適解が求められていることが分かります。
また重なって分かりにくいですが、負荷のあるケース②の方が反復数が多い傾向にあることが分かります。
以下のGifは2つのケースの実験結果を収めたアニメーション(4倍速)です。
(スマホで撮ったので手ブレがだいぶあります苦笑)
終わりに
今回はMBDのワークフローを意識して制御系設計を行ってみました。
あくまで個人の趣味の範囲なので簡単に実施していますが、実際の製品開発では基本設計や検証フェーズに重点を置いて、さらに詳細かつ厳格な対応を行っています。
特に自動車や航空機の業界ではソフトウェアの機能安全という文化が浸透し、規格に準拠した開発を行っていることが多いようです。(ISO26262とかDO-178Cとかとか)
自分もまだまだ勉強している身ではありますが、MBDって何だろうという人に本記事が少しでも参考になれば。












