時系列予測モデリング ~将来の電力需要を予測する~

はじめに

今冬、国内の電力需給がかなり厳しいと言われる中、電力会社各社では休止中の電源（火力）の再稼働、再エネの最大限活用、需要者側のデマンドレスポンス普及対策、需要家の節電効果など各種施策によって、供給の予備率3%をなんとか確保できる見込みが立っています。

【参考】
・経済産業省 2022年度冬季の電力需給対策資料
・JERAプレスリリース 2022年度の冬季重負荷期の需給対策について

ところで、なぜ3％なのか。
資源エネルギー庁によると需要には3%程度のブレがあるためとされています。

・資源エネルギー庁 電力需給状況

以前の記事でも紹介したように電気は、いま使っている電気と同じ分だけ発電することで安定的に利用することが出来ます。
これを同時同量と呼び、発電、送電事業者は毎日30分単位で1日の需要と供給力を合わせ込むように発電計画を立てて運用しています。
もちろん、発電計画通りにシナリオが進むばかりではなく、また30分よりも早い周期での変動もあるため、電力の制御では系統慣性（タービン発電機の慣性力）、ガバナフリー(GF)、LFC、EDC（発電計画）といういくつかの応答速度の異なる制御を使い分けて行われています。
発電所の制御は過去の記事で少し紹介しています。

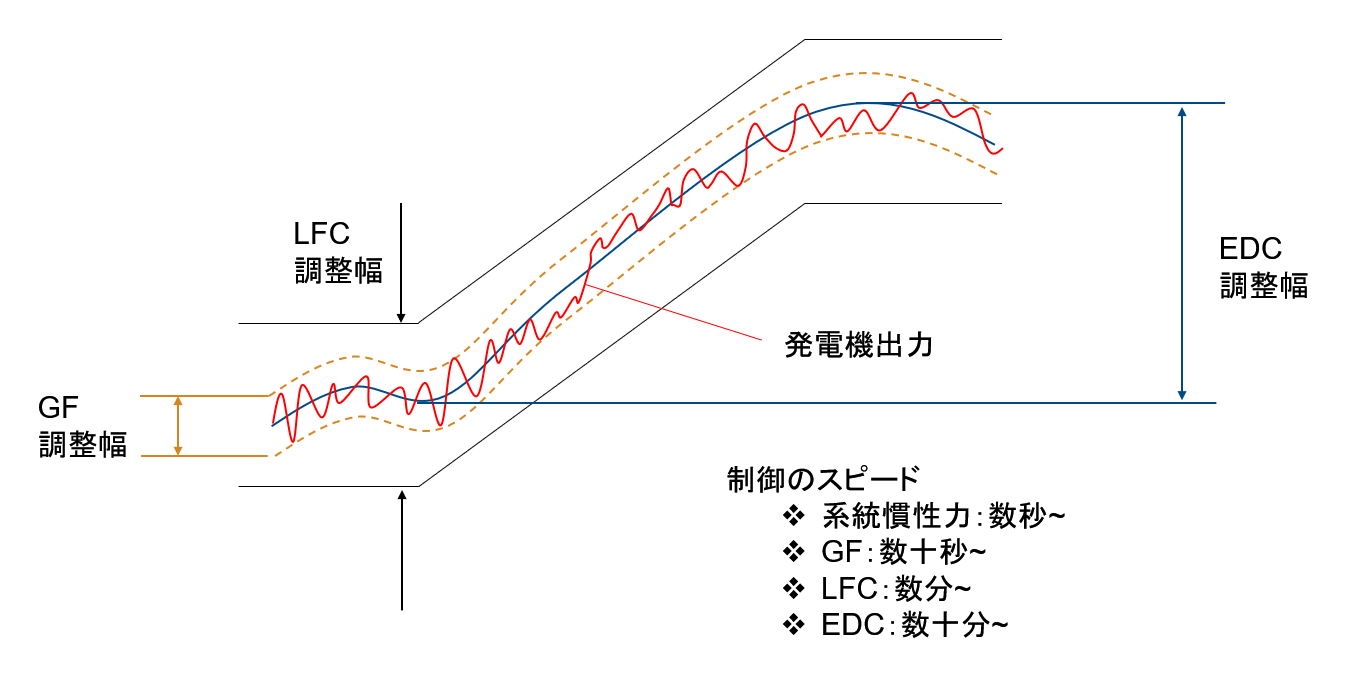
（参考：資源エネルギー庁 需給調整市場について）

ただし、想定外の気象変動や電力需要の伸びがあったり、発電所がトラブルで運転できなくなった場合、供給力が不足し、予備率3%を下回る危険水域となります。
特に関東首都圏では、現在、設備が古く休止されていた火力発電所をメンテナンスしてフル稼働させていますので、故障などのトラブルで停止してしまう恐れを含んでいます。
火力は100万kW(原発1基クラス)の大型電源もあるため、それが一基停止することによる損失は計り知れません。

実際、2022年の6月末にあった首都圏の需給ひっ迫時には、福島の勿来火力発電所9号機（60万kW）がボイラー設備トラブルによって緊急停止してしまい、それが異例の猛暑による冷房需要増加に重なり、予備率が1%を切るブラックアウト目前のかなり危ない状態に陥っていました。
この時は、元々2022年7月1日から再稼働を計画していた姉崎火力発電所5号機（60万kW）を前倒しで稼働することで何とか凌げたということのようです。
この姉崎5号機も老朽化で休止していた火力でありますが、夏場の重負荷期に対応するために再稼働を決めていました。

【参考】
ABEMA NEWS 「停電もありえた」電力危機救った“姉崎”

そういった中で、いかに精度良く将来の電力需要を予測するかが、安定供給やコスト削減のカギとなってきます。
なぜなら、精度の高い予測ができれば、確度の高い発電計画が作れるからです。
需要予測の分野では、近年AIや機械学習によるデータドリブンなアプローチが主流となってきています。
電力需要予測は既にPythonによる方法などいくつもの記事がありますが、ここではMATLABを使ってやってみたいと思います。

浅いニューラルネットワーク及びLSTMによる電力需要予測

それでは、実際に電力需要予測を行うためのプログラミングを行っていきます。
今回は、曜日や時間、過去の需要実績、気温を学習データとして将来の電力需要を予測する予測モデルを開発します。
予測モデルには、古典的な3層のフィードフォワードニューラルネットワーク及びLSTMの2つを用意して性能の比較を行います。

データ取得

まずは電力需要の過去の実績データおよび気温のデータを取得します。
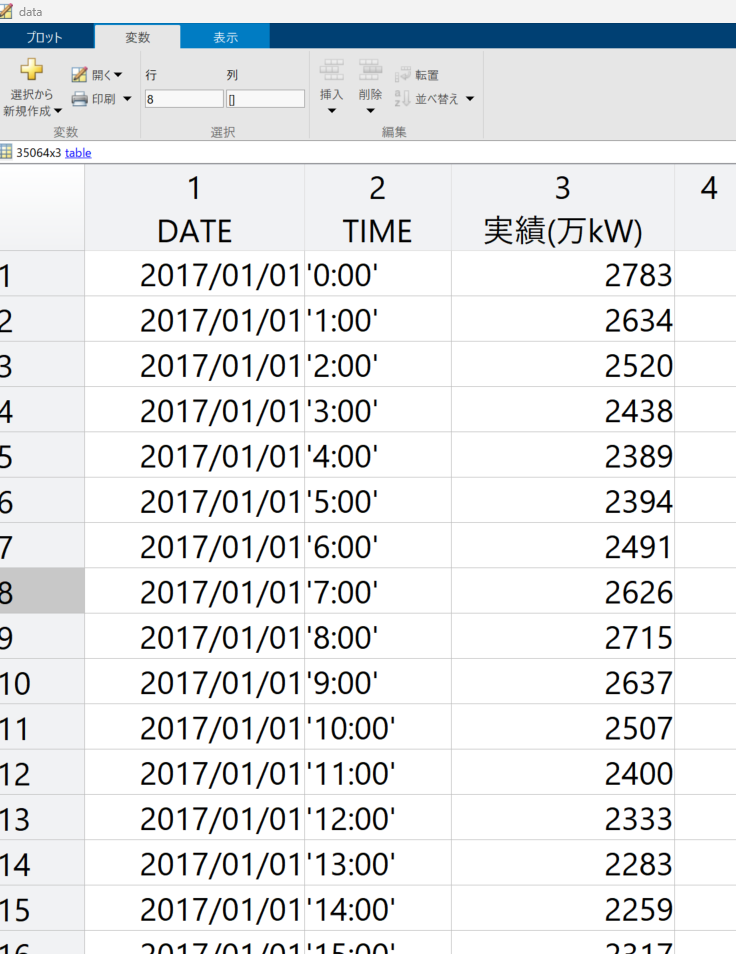
電力需要の実績データは東京電力パワーグリッドが提供しているデータを使用します。

東京電力パワーグリッド 過去の電力使用実績データ

データを取得するためのコード例は以下

データ取得のコード

data = [];
years = [2017 2018 2019 2020]; % 取得期間

for i = 1:length(years)
    str = "https://www.tepco.co.jp/forecast/html/images/juyo-" + num2str(years(i)) + ".csv";
    data = [data; readtable(str,VariableNamingRule="preserve") ];
end

csvデータ等の取り込みについてはtableデータ型形式で読み込み可能なreadtable関数を利用できます。
この関数の引数に読み込むcsvデータのURLパスを文字列で与えれば、ネットからも読み込み可能です。
上記コードでは2017年～2020年までの4年間を訓練データとして活用するためにforを回して年数のところだけを可変にした文字列strによってデータをreadtableによって読み出し、結果をdataという空の配列に行方向に繋げていく処理を行っています。
実際に実行すると以下のイメージとなります。

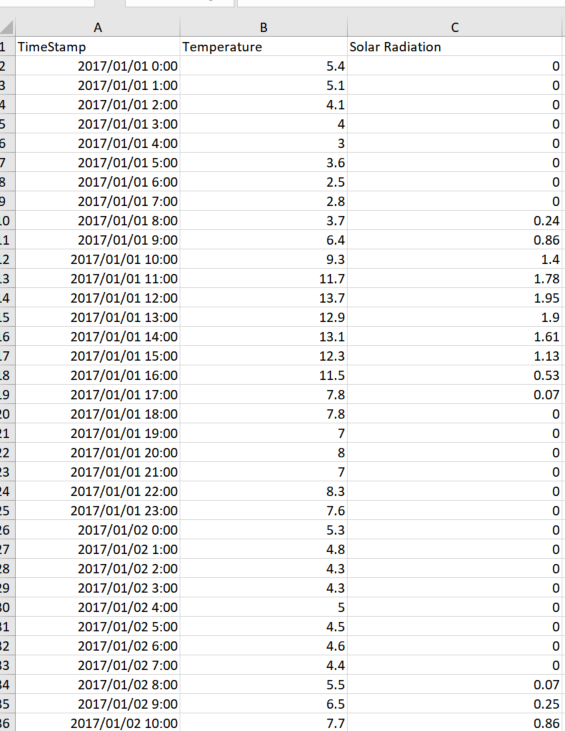
また気温については、気象庁のHPからcsvでダウンロードできますが、いろいろと選択項目があり、かつ1回でダウンロードできるデータ容量に限りがあるため、少々手間ですが、一つ一つ気温データをダウンロードしていきます。
ちなみに取得するのは東京の気温データ（1時間毎）です。

気象庁 過去の気象データ・ダウンロード

直接ダウンロードしたデータでは余計な文字列や情報があるため、少しだけ手作業で加工して以下のようにしておきます。
（太陽の日射量を含んでいますが、今回は使いませんでした）

電力需要と気温データを便宜上一つのデータに繋げておきます。
そこで、上記のreadtable関数の処理を修正して最終的には以下のようにします。

訓練データの取得コード

data = [];
years = [2017 2018 2019 2020]; % 取得期間

for i = 1:length(years)
    str1 = "https://www.tepco.co.jp/forecast/html/images/juyo-" + num2str(years(i)) + ".csv";
    str2 = "weatherData_" + num2str(years(i)) + ".csv";
    data = [data; [readtable(str1,VariableNamingRule="preserve") readtable(str2,VariableNamingRule="preserve")]];
end

date = string(data.DATE);
time = data.TIME;
str_datetime = date + ' ' +time;
dt = datetime(str_datetime);
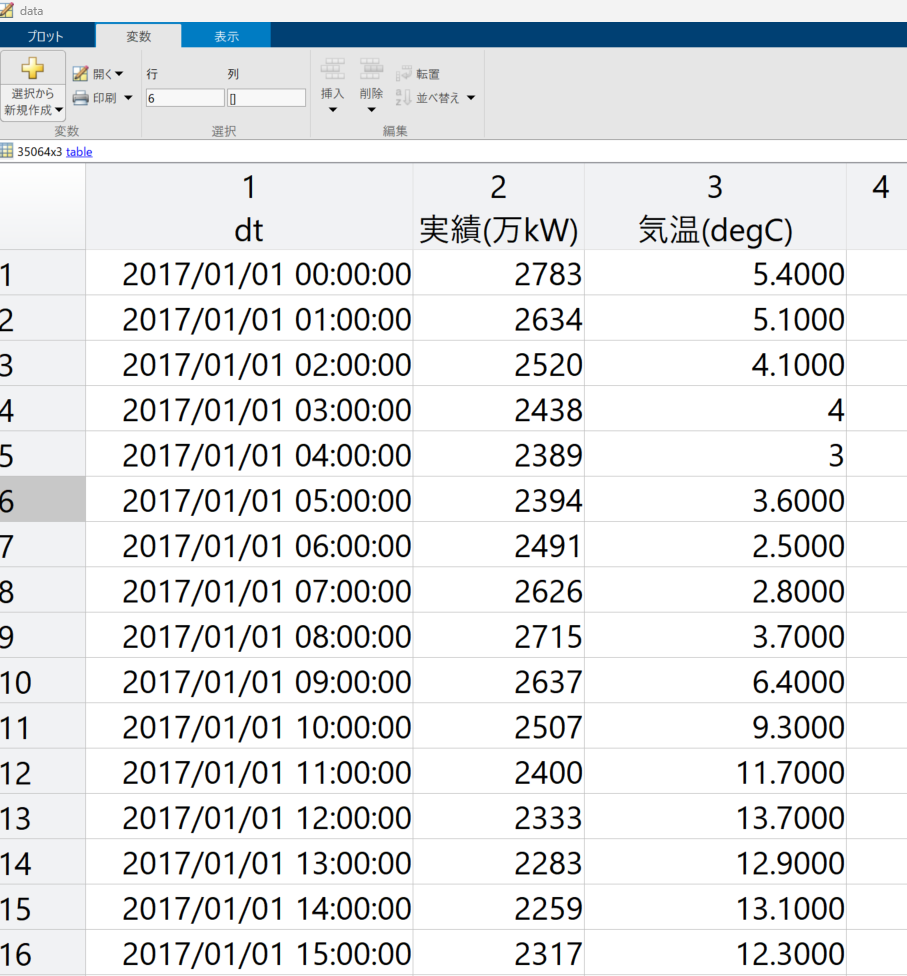
data = table(dt,data.("実績(万kW)"),data.("Temperature"),VariableNames={'dt','実績(万kW)','気温(degC)'});

上記コードではreadtable関数を2回読んで、各年の電力と気象のデータを列方向に繋いだ後、data配列に行方向で繋いでいっています。
その後は、日時情報をdatetime型に変換して、最終的には日時と需要、気温を要素に持つ下記のテーブルデータを作成します。

同じ要領で検証用のデータも用意しておきます。
検証データは2021年1月～2022年12月（作成日時点まで）までのデータです。

検証データの取得コード

test_data = [];
test_years = [2021 2022];
for i = 1:length(test_years)
    str1 = "https://www.tepco.co.jp/forecast/html/images/juyo-" + num2str(test_years(i)) + ".csv";
    str2 = "weatherData_" + num2str(test_years(i)) + ".csv";
    test_data = [test_data; [readtable(str1,VariableNamingRule="preserve") readtable(str2,VariableNamingRule="preserve")]];
end

date = string(test_data.DATE);
time = test_data.TIME;
str_datetime = date + ' ' +time;
dt = datetime(str_datetime);
test_data = table(dt,test_data.("実績(万kW)"),test_data.("Temperature"),VariableNames={'dt','実績(万kW)','気温(degC)'});

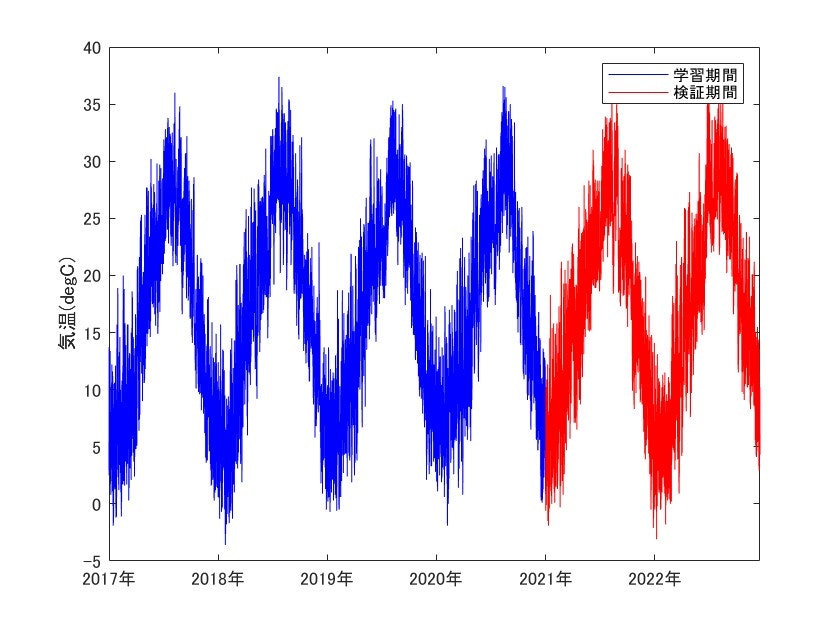
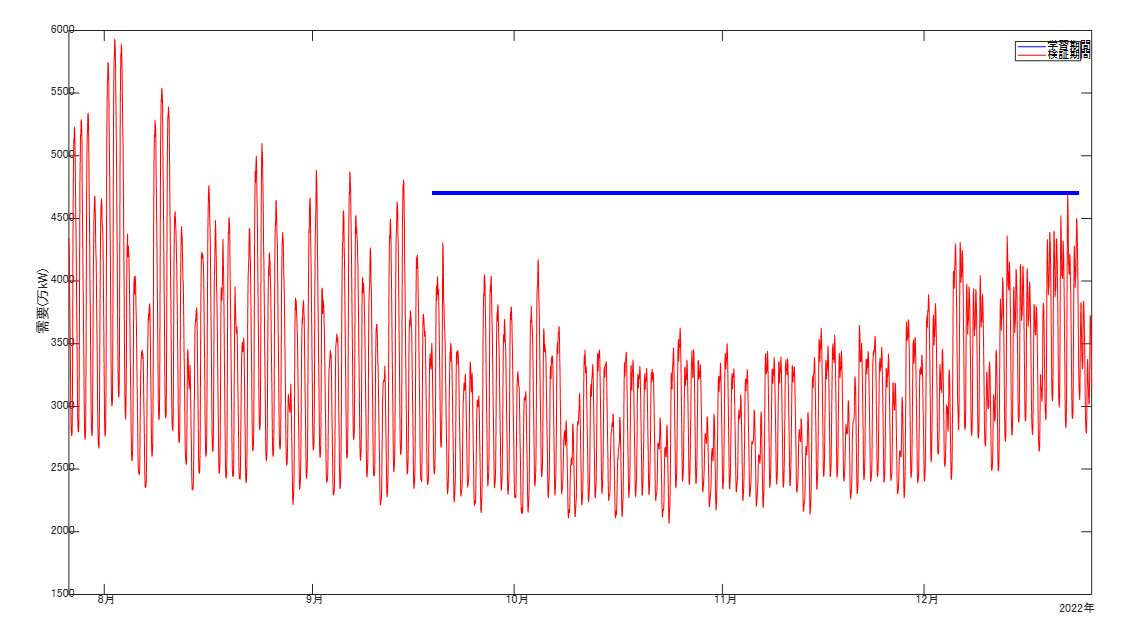
取り込んだデータを描画して確認しておきます。

可視化のコード

figure,clf
plot(data.dt,data.("実績(万kW)"),'b-'),hold on
plot(test_data.dt,test_data.("実績(万kW)"),'r-'),hold off
ylabel('需要(万kW)')
legend('学習期間','検証期間')

figure,clf
plot(data.dt,data.("気温(degC)"),'b-'),hold on
plot(test_data.dt,test_data.("気温(degC)"),'r-'),hold off
ylabel('気温(degC)')
legend('学習期間','検証期間')

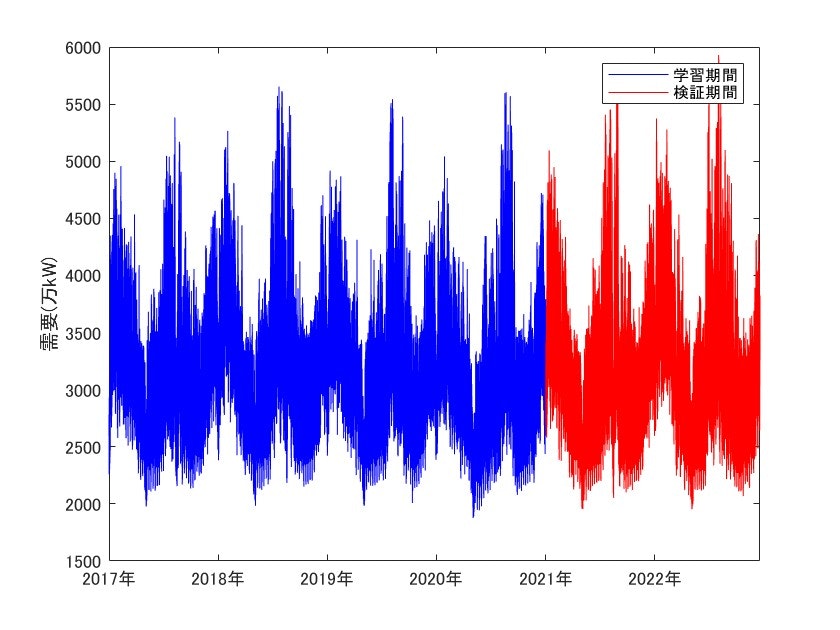
上図はそれぞれ需要(万kW)と気温のグラフであり、青が訓練に使用するデータ、赤が検証に使用するデータです。
図を見ての通り、需要は周期性のある波形となっています。
夏季に需要のピーク（約5500万kW）を迎えるのに加え、冬季にも夏季ほどではありませんが高いピークがあります。
また需要は気温との有意な相関があることが分かっています。
グラフを見比べてみると、夏場の最高気温を計測するあたりが年間の最高需要と当たっており、また冬場の最低気温を迎えるあたりでも需要のピークに当たっているのが分かります。

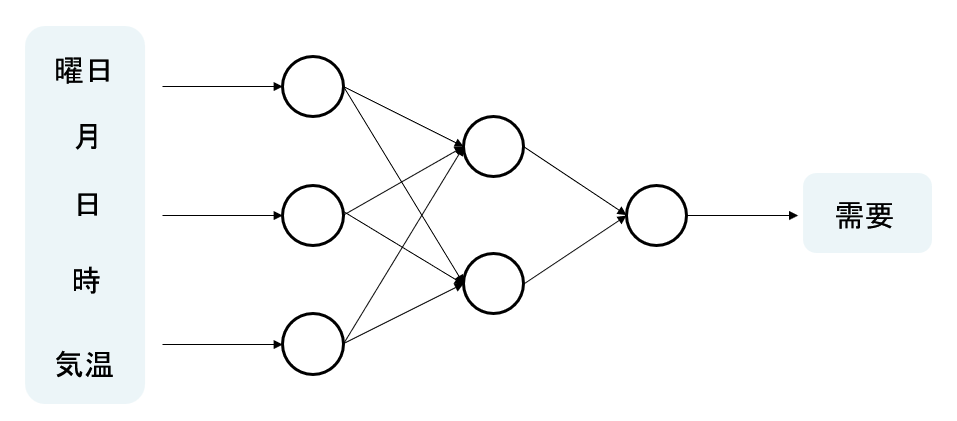
続いて、訓練データを各予測モデルに与えるために、加工していきます。
予測モデルに与える入力は下図の通り、曜日、月、日、時、気温の5つであり、そこから需要(万kW)を予測します。

訓練データの前処理のコード

dweekday = weekday(data.dt);
dhour = hour(data.dt);
dmonth = month(data.dt);
dday = day(data.dt);
dload = data.("実績(万kW)");
dtemp = data.("気温(degC)");
dtemp = fillmissing(dtemp,'linear');       % 欠損値を線形補間
traindata = [dweekday dhour dmonth dday dtemp dload];

% 正規化処理
XTrain = traindata(:,1:end-1)';
TTrain = traindata(:,end)';
[XTrain,XTs] = mapminmax(XTrain);
[TTrain,TTs] = mapminmax(TTrain);

MATLABではdatetimeから曜日や月数などを数値データとして抽出する関数が各々用意されているため、それを使って入力データを作っていきます。
また気象庁のデータには欠損値が一部含まれているため、欠損値をその前後のデータを利用して線形補間して埋める処理をfillmissing関数を使ってやっておきます。

最後に、訓練データは様々な単位を有しており、それを直接予測モデルの学習に使用すると数値オーダーのバラつきによって適切に学習ができない可能性があるため、データをあらかじめ正規化してオーダーをそろえておくことが有効です。
MATLABではDeep Learning Toolboxよりデータを[-1,1]の範囲で正規化してくれるmapminmax関数があるので、これを使用して前処理を施しておきます。

同じ要領で検証データにも前処理を施しておきます。

検証データの前処理のコード

dweekday = weekday(test_data.dt);
dhour = hour(test_data.dt);
dmonth = month(test_data.dt);
dday = day(test_data.dt);
dload = test_data.("実績(万kW)");
dtemp = test_data.("気温(degC)");
dtemp = fillmissing(dtemp,'linear');      % 欠損値を線形補間
testdata = [dweekday dhour dmonth dday dtemp dload];
XTest = testdata(:,1:end-1)';
TTest = testdata(:,end)';
[XTest,~] = mapminmax('apply',XTest,XTs);

なお、正規化処理では訓練データで算出したスケーリングを以降の処理でも使っていきます。
そのため、検証データの正規化処理時にはmapminmax関数の引数に訓練データのスケーリング値を渡して適用させています。

ネットワークの設計と学習

データの準備ができたので、続いては予測モデルの設計と学習を行っていきます。
MATLABのDeep Learning Toolboxでは古典的な浅いニューラルネットワークの設計に加えて、深層学習ネットワークの設計も行うことが出来ます。

先述の通り、今回は予測モデルとして3層のフィードフォワードニューラルネットワーク（以後NNと略記）とLSTMの2つを利用するため、それぞれの予測モデルを設計していきます。

まずNNの設計においては、関数近似を行うニューラルネットワークを設計するための関数fitnetを利用します。
関数の引数には隠れ層の個数を与えることができ、これがハイパーパラメーターの一つです。

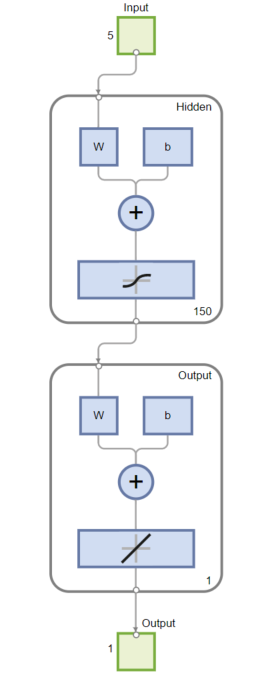
今回は150個の隠れ層ユニットを持つネットワークとしていきます。

NNの設計コード

numChannels = size(XTrain,1);

% 浅いNNでの学習
hiddenSizes = 150;
shallow_net = fitnet(hiddenSizes);

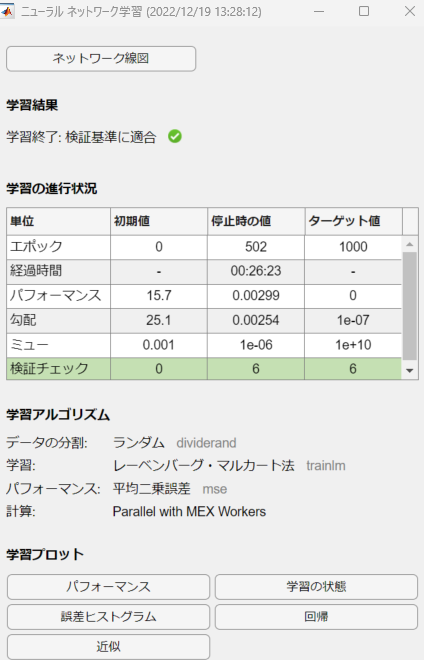
ネットワークが構成出来たら、train関数を呼び出して、引数にNN、訓練データ（入力＆出力）を与えて実行するだけで訓練が始まります。
ちなみに、Parallel Computing Toolboxという製品があるとuseParallelオプションによってCPUを使った並列計算によって学習を進めることが出来ます。
（※並列化したからといって全てのケースで学習時間が短縮化されるわけではないので注意）

NNの学習コード

shallow_net = train(shallow_net,XTrain,TTrain,useParallel='yes');

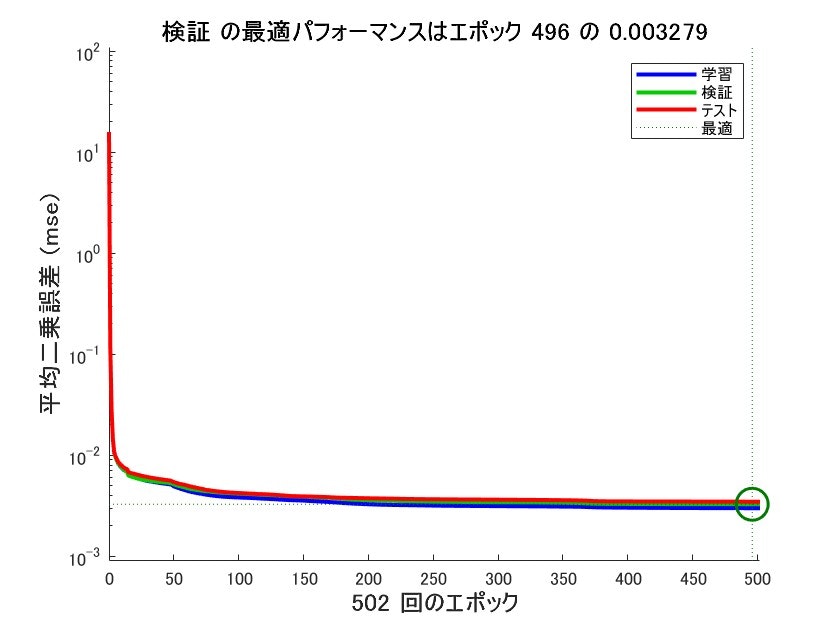
学習中に進捗状況や性能を確認することが出来ます。
結果から有限のエポック内で学習が収束し、回帰直線にも載っているので性能もそこそこあることが分かります。

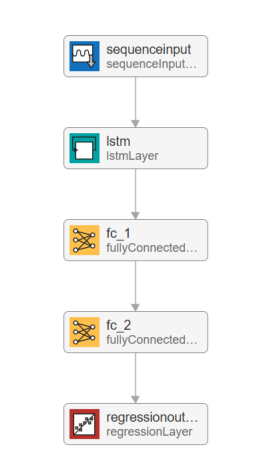
続いて、LSTMの設計を行っていきます。
LSTMを含む深層学習ネットワークの設計では、あらかじめ用意されているレイヤーを組み合わせていくことで任意の構成でネットワークを構築することが出来ます。
今回はLSTMレイヤーを加え、かつ全結合層を2つ繋げることでLSTMを構成します。

LSTM及び1つ目の全結合層のユニット数は20個とします。

LSTMの設計コード

hiddenSizes = 20;
numChannels = size(XTrain,1);
layers = [
        sequenceInputLayer(numChannels)
        lstmLayer(hiddenSizes)
        fullyConnectedLayer(hiddenSizes)
        fullyConnectedLayer(1)
        regressionLayer];

ネットワークの設計ができたら、学習のための各種オプションを指定し、trainNetwork関数に食わせることで学習が始まります。
LSTMでも並列計算のオプションに加え、GPUでの計算もマシンによっては行うことが可能です。

LSTMの学習コード

options = trainingOptions("adam", ...
        InitialLearnRate=0.005, ... 
        MaxEpochs=3000, ...
        Plots="training-progress", ...
        Shuffle="every-epoch", ...
        ExecutionEnvironment="parallel", ...
        Verbose=0);
    
lstm_net = trainNetwork(XTrain,TTrain,layers,options);

学習進行中では、RMSE値に加え、損失値も表示されます。

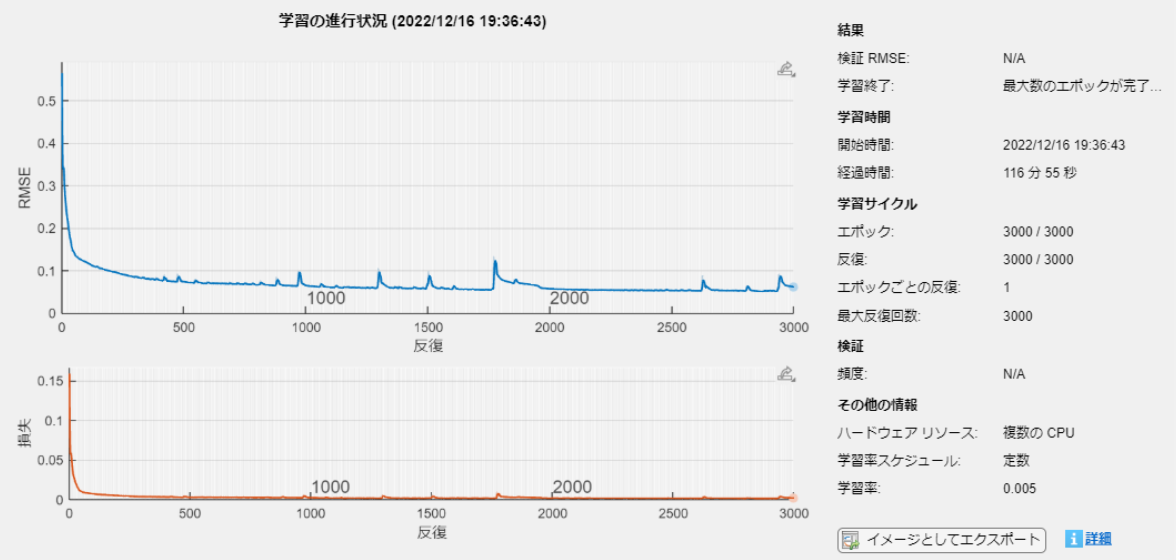
LSTMも学習が大体収束し、損失がかなり小さくなっているのでそこそこ性能を期待できそうです。

検証実験

前の章で予測モデルの構築ができたので、検証データを使って各モデルの性能を確かめてみます。

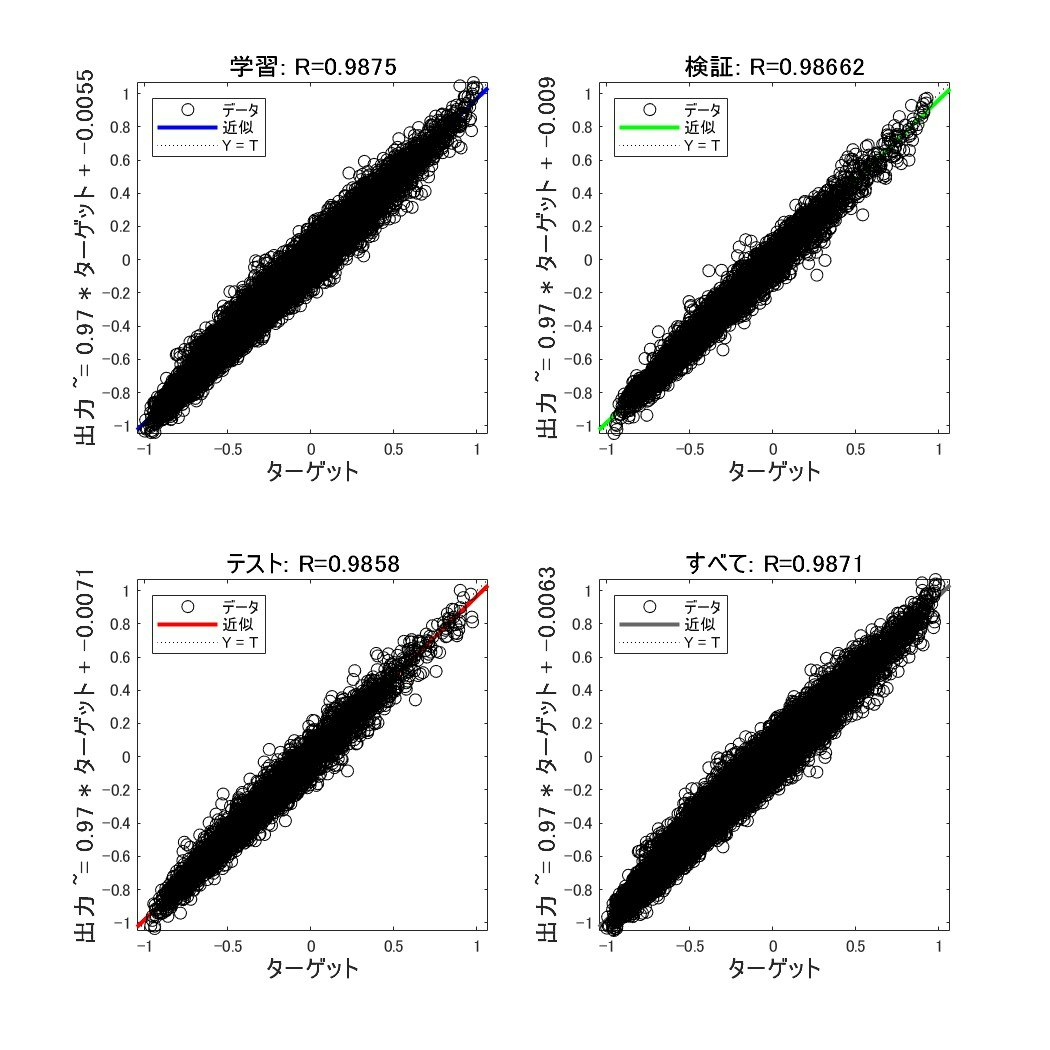
まずはNNの方から結果を掲載します。
予測を実行するのは簡単で、学習済みネットワークにデータを入力するだけです。

NNの予測実行のコード

yhat = shallow_net(XTest);

結果を次の図に示します。

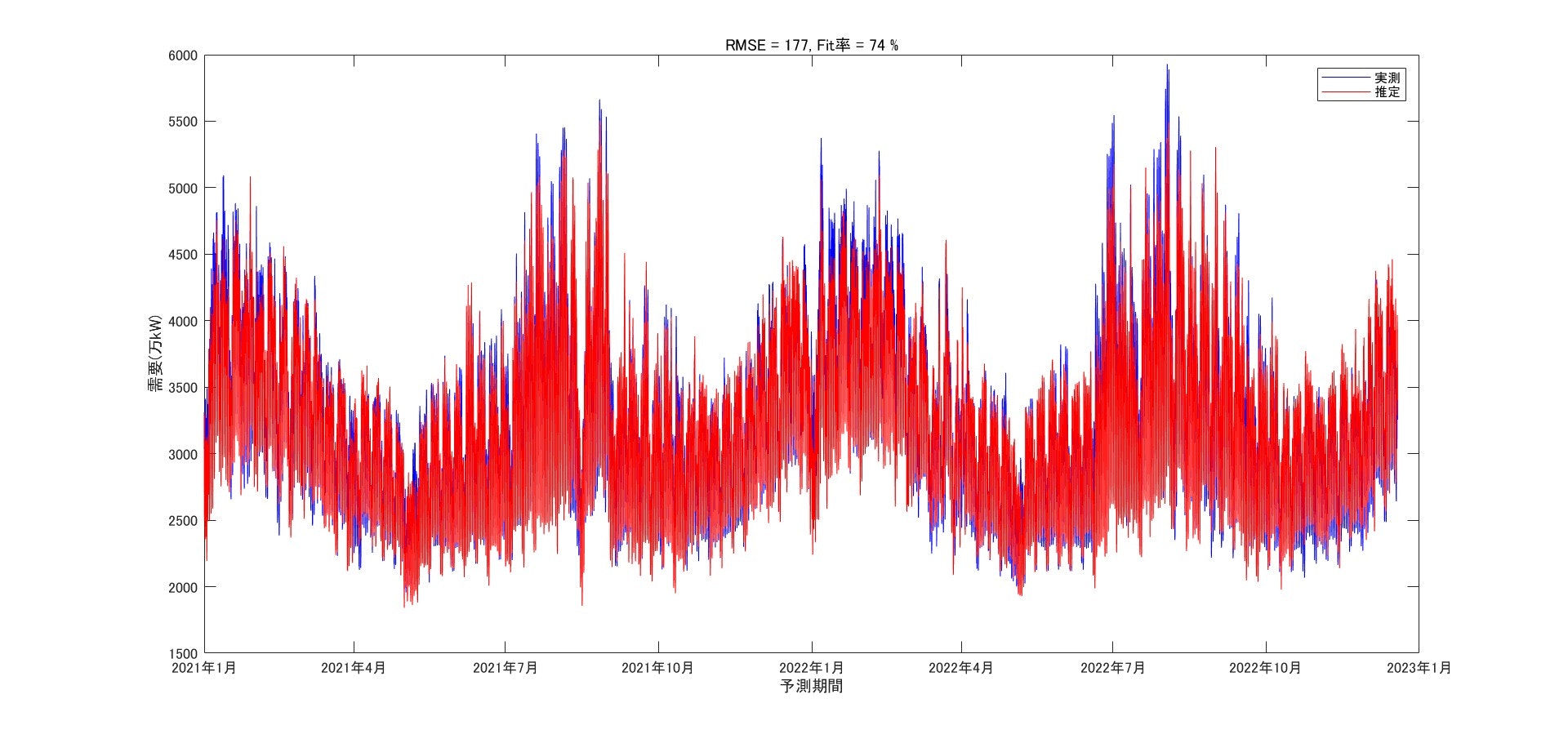
図中、青が実測、赤が予測ですが、概ね全体の傾向は捉えており、まずまずの予測性能と言えそうです。
図中にデータに対する一致率を評価する指標としてRMSE値とFit率を表示しています。
特にFit率＝74％ということで、まずまず合ってそうだと評価できます。
細かいところを拡大して見てみます。

ピーク値の誤差が多少ありますが、的外れな値ではなさそうです。

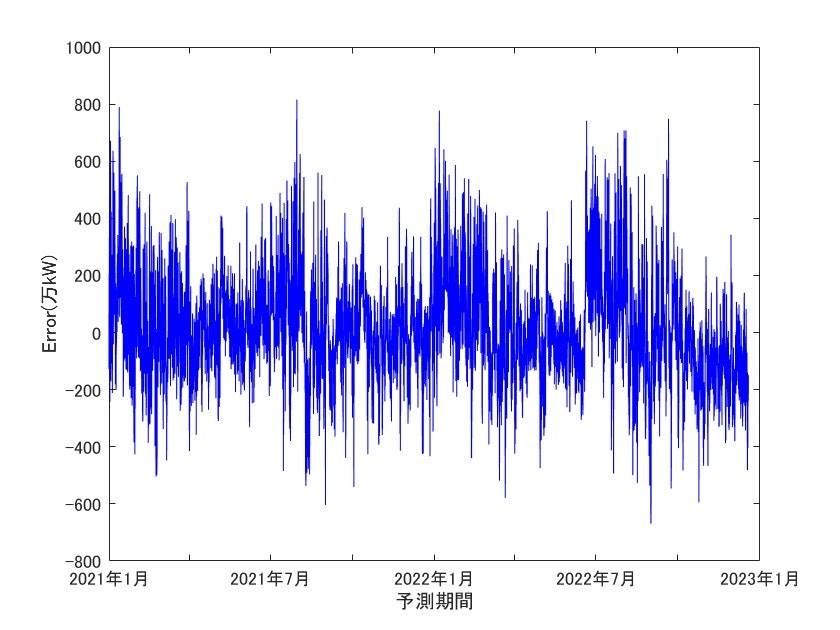
誤差(実測-予測)の図も掲載します。最大で800万kW程度の誤差があります。

続いて、同じデータに対するLSTMの予測を行います。
LSTMでは、内部の各状態をリセットし、かつ学習データを使って更新した上で、predict関数によって予測を行います。

LSTMの予測実行のコード

resetState(lstm_net);
[lstm_net,~] = predictAndUpdateState(lstm_net,XTrain);
yhat = predict(lstm_net,XTest);

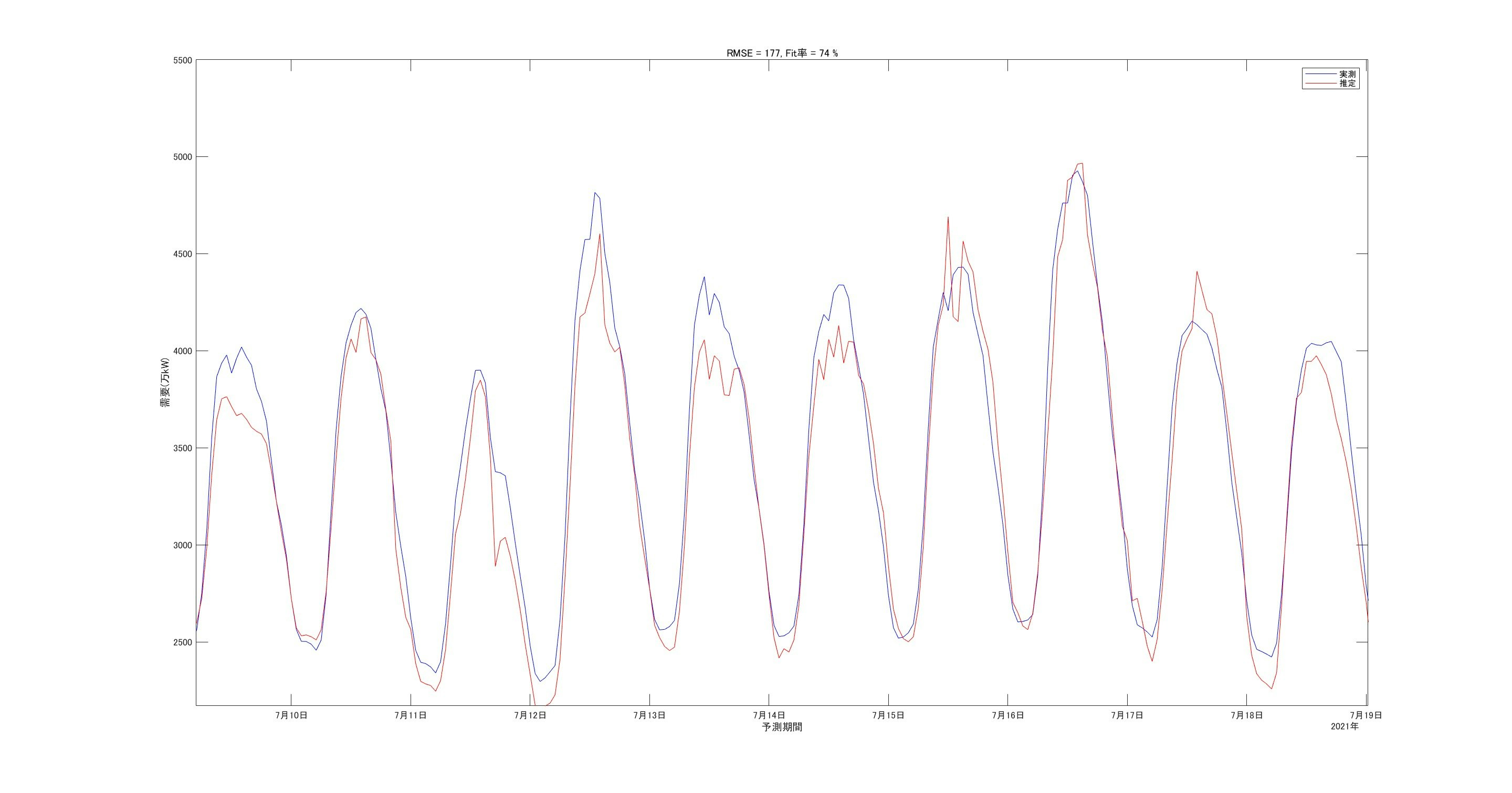
結果は次の通りです。

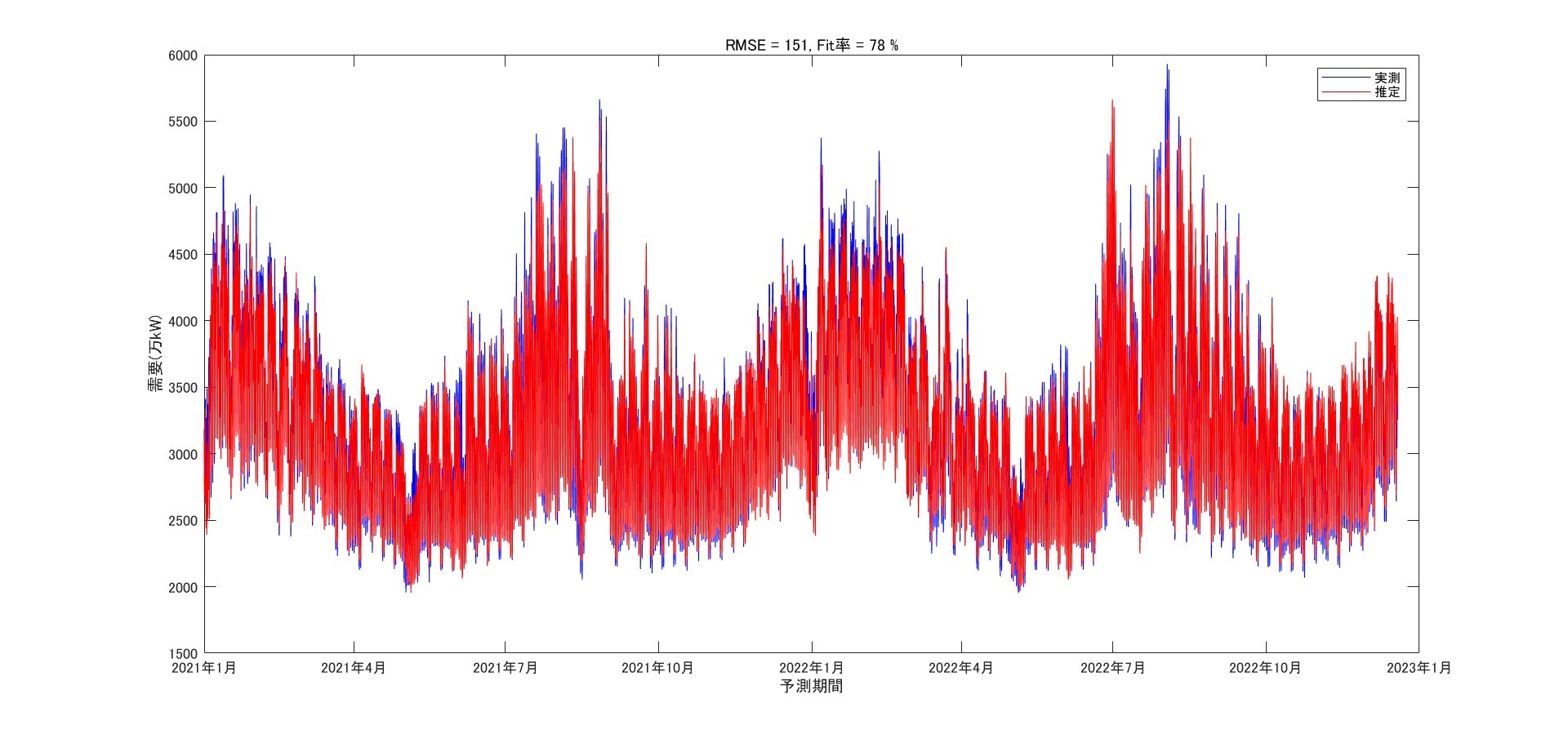
先ほどのNNと比較して、LSTMの方がRMSE（=151）及びFit率（＝78%）含め改善されています。

細かい部分を拡大して見ます。


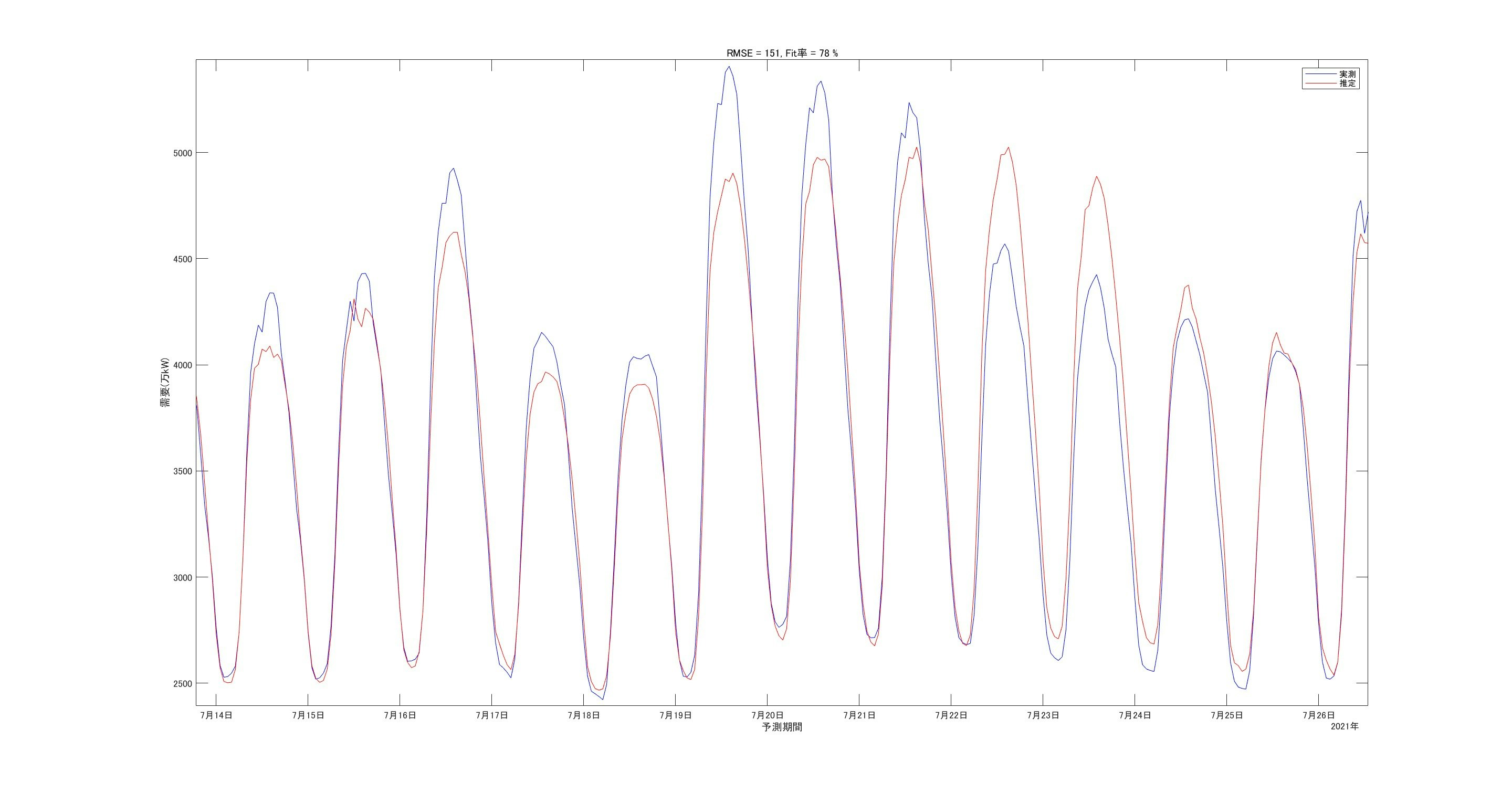
こちらもピーク値のずれはありますがそこそこの予測性能はありそうです。

誤差の結果も掲載します。

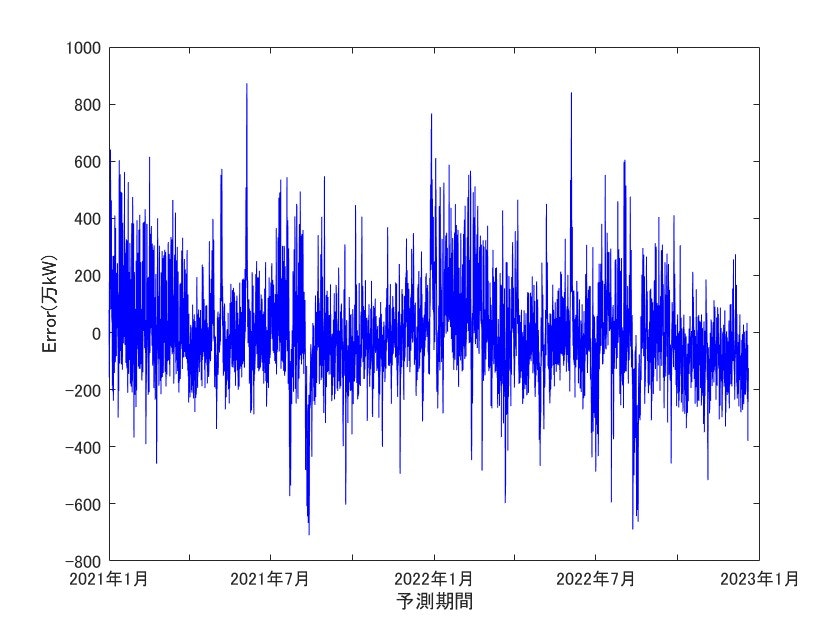
こちらも最大で800万kW程度の誤差が出ています。
波形からなかなかに優劣はつけられませんが、RMSE及びFit率から定量的にLSTMの性能を確認することが出来ます。

(※今回はハイパーパラメーターをそこまで振っていませんので、頑張ればもっと性能が出る可能性はあります)

結果の処理や指標の計算関連のコード

% 非正規化処理
yhat = mapminmax('reverse',yhat,TTs);

% RMSEの計算
n = length(TTest);
rmse = sqrt(sum((TTest - yhat).^2)/n);

% Fit率
fit = 100 * (1 - norm(TTest - yhat)/norm((TTest - mean(yhat))));

figure,clf
plot(test_data.dt,TTest,'b-'),hold on
plot(test_data.dt,yhat,'r-'),hold off
ylabel('需要(万kW)')
xlabel('予測期間')
legend('実測','推定')
title(sprintf('RMSE = %d, Fit率 = %d %%',fix(rmse),fix(fit)))

figure,clf
plot(test_data.dt,TTest - yhat,'b-')
ylabel('Error(万kW)')
xlabel('予測期間')

最後に

では最後に将来の需要予測（なんちゃってでんき予報）を行って締めたいと思います。
予測するのは東京電力管内における2022年12月20日 0:00 ～ 2022年12月23日の10:00までの需要です。
この際、気温の1時間ごとの予報データはウェザーニュースから引用し、手元にインプット用のcsvファイルを用意しておきます。

データ作成時点での4日間の気温のグラフはこんな感じ↓

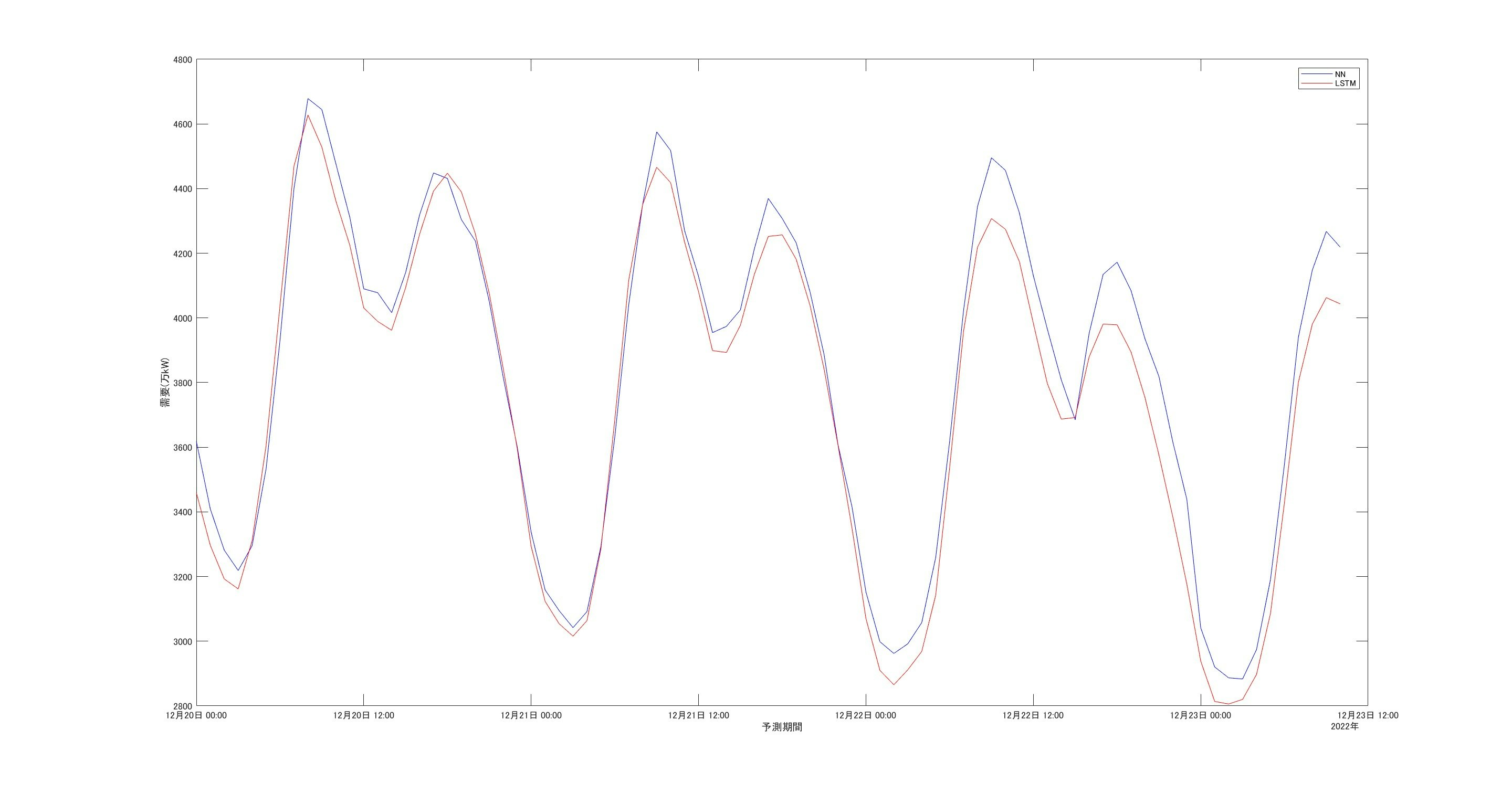
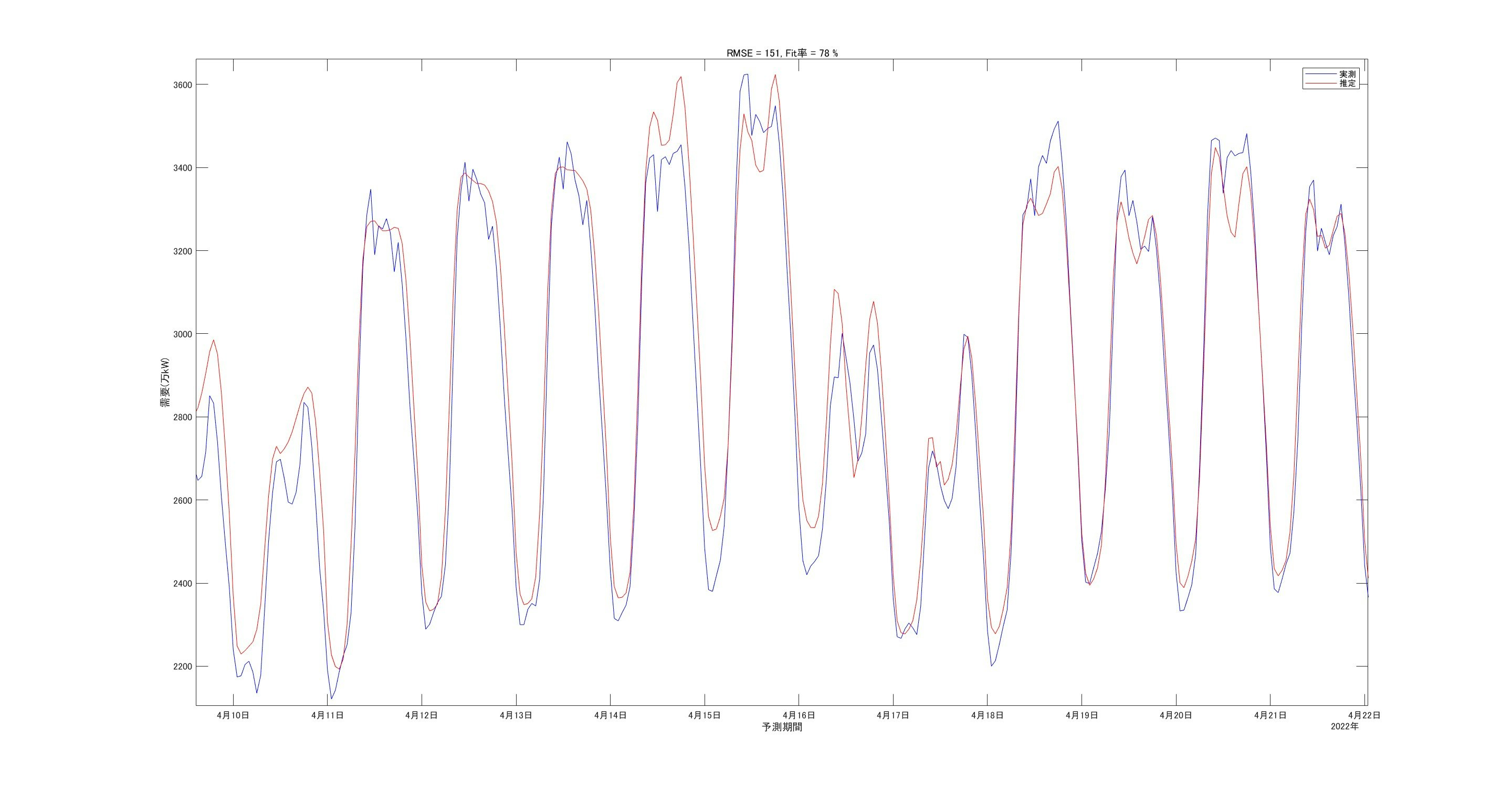
上記のデータをインプットしたときの各需要予測値は以下のようになりました。

NNとLSTMによる予測値↓

見た感じ2つとも大体同じような波形となっていますが、NNの方がLSTMに対し、若干バイアス高めに予測しています。
また週末にむけて需要が落ちていっています。この時期はクリスマスや冬休みもあったりで学校や会社での需要が減って、少し落ち着くのかもしれませんね。
時間が許せば、答え合わせをしたいと思います。

なんちゃって予報のコード

str = "weatherData_2022_forecast.csv";
read_data = readtable(str,VariableNamingRule="preserve");
dt = datetime(read_data.('TimeStamp'));
forecast_data = table(dt,read_data.("Temperature"),VariableNames={'dt','気温(degC)'});

% 気温の予報データを描画
figure,clf
plot(forecast_data.dt,forecast_data.("気温(degC)"),'b-')
ylabel('気温(degC)')

% 入力データの作成
dweekday = weekday(forecast_data.dt);
dhour = hour(forecast_data.dt);
dmonth = month(forecast_data.dt);
dday = day(forecast_data.dt);
dtemp = forecast_data.("気温(degC)");
dtemp = fillmissing(dtemp,'linear');      % 欠損値を線形補間
indata = [dweekday dhour dmonth dday dtemp];
[indata,~] = mapminmax('apply',indata',XTs); % 訓練データの値で正規化

% 需要予測
% 浅いニューラルネットワーク
yhat_shallow = shallow_net(indata);

% LSTM
resetState(lstm_net);
[lstm_net,~] = predictAndUpdateState(lstm_net,XTest);
yhat_lstm = predict(lstm_net,indata);

% 単位を元に戻す
yhat_shallow = mapminmax('reverse',yhat_shallow,TTs);
yhat_lstm = mapminmax('reverse',yhat_lstm,TTs);

figure,clf
plot(forecast_data.dt,yhat_shallow,'b-'),hold on
plot(forecast_data.dt,yhat_lstm,'r-'),hold off
ylabel('需要(万kW)')
xlabel('予測期間')
legend('NN','LSTM')

今回は時系列予測として電力需要予測を行いました。
予測精度としては7割程度ということで、まだ信頼に足り得るものには達していません。
現在、気象会社や電力会社、メーカー各社などでは実際に高精度な予測モデルを開発し、サービス提供を行っています。
どういったモデルを使うか、またどのようなデータを使うかが予測モデルの精度に直結していきます。

予報の答え合わせ

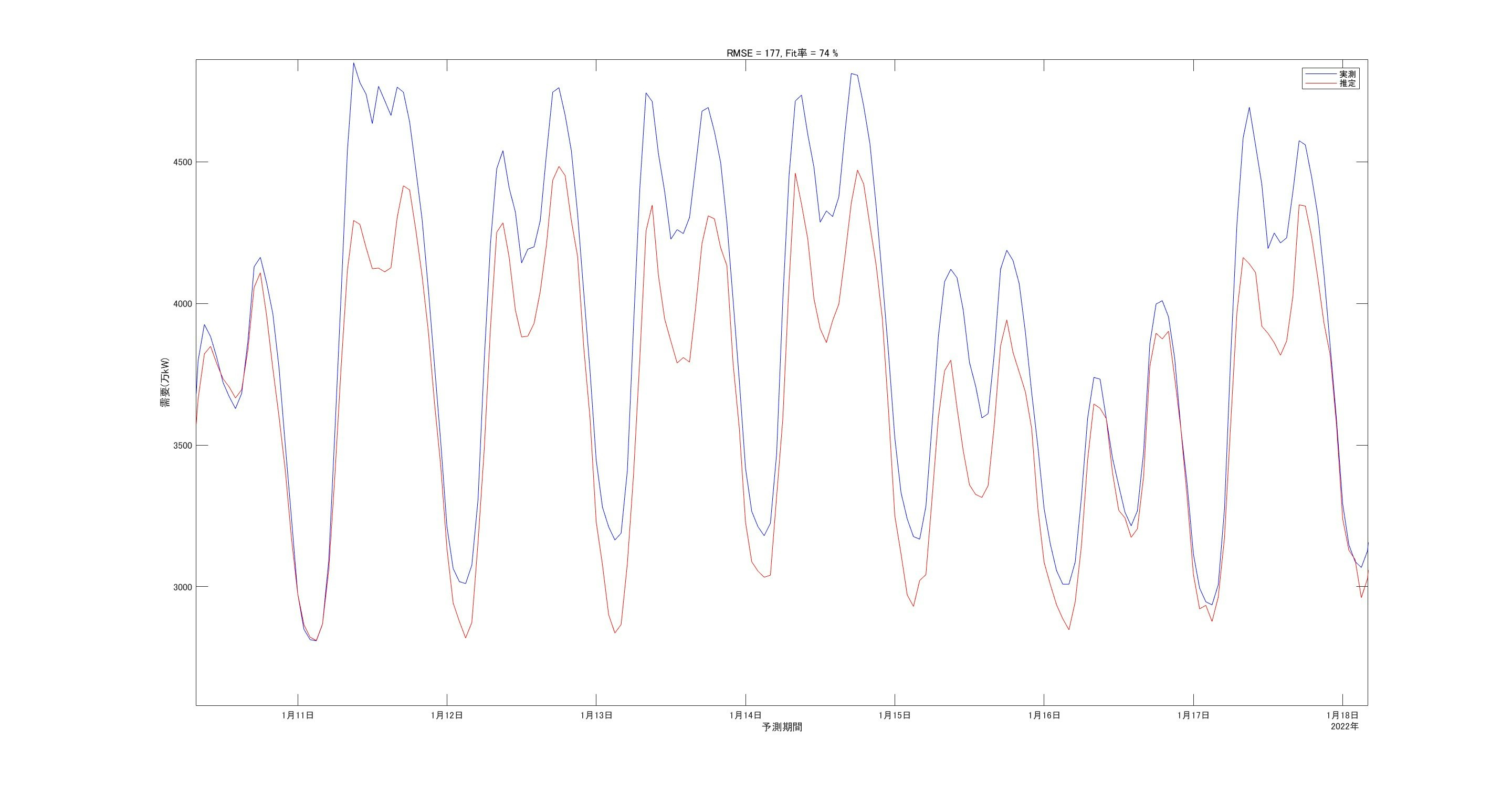
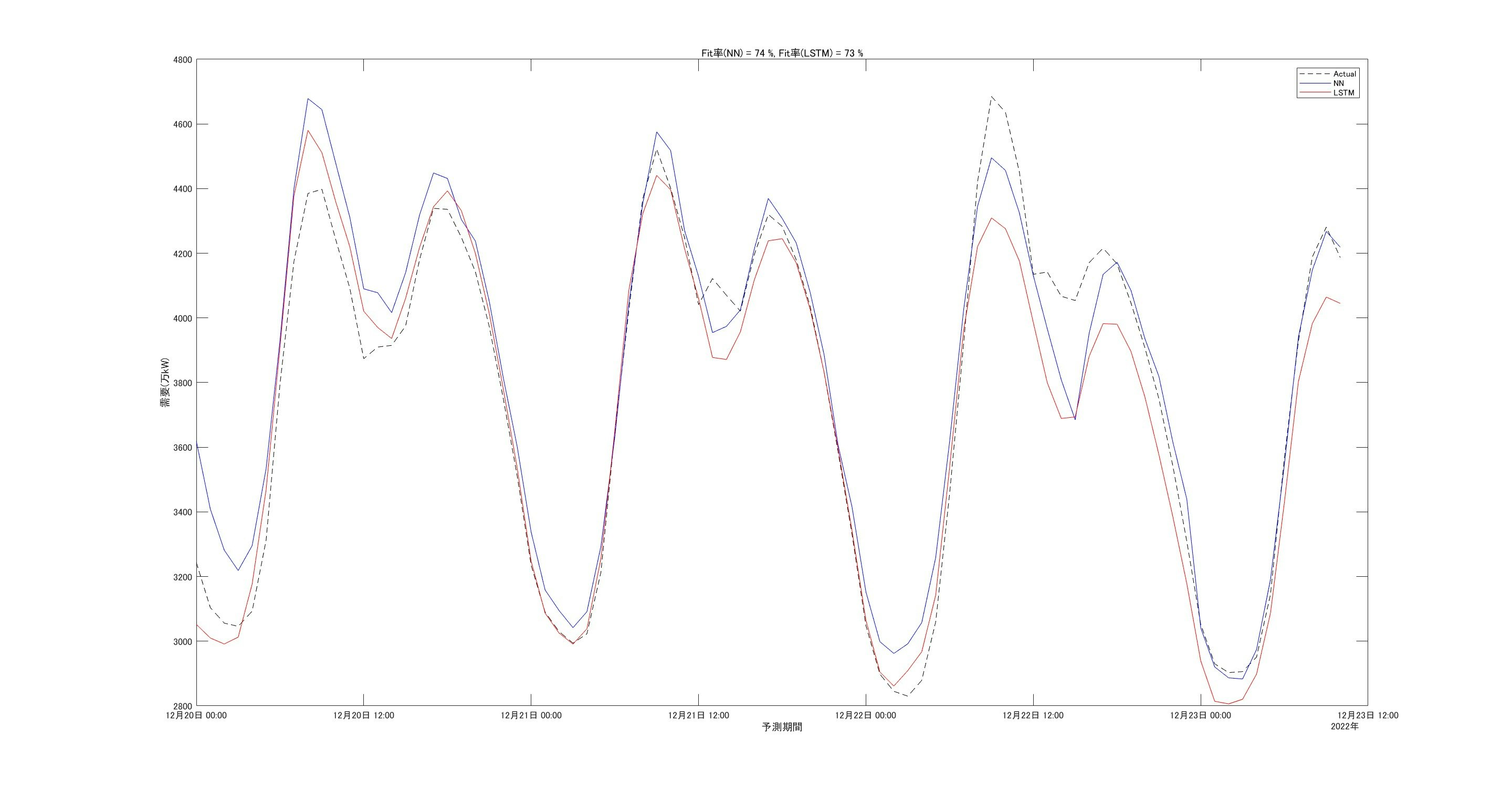
データが更新されたので、予報の的中精度を確認してみたいと思います。
LSTMの方では、状態の初期化に使う過去の実績データ数が少々増えているので前の予報値と少し変わってしまっていますがご愛嬌ということで。。

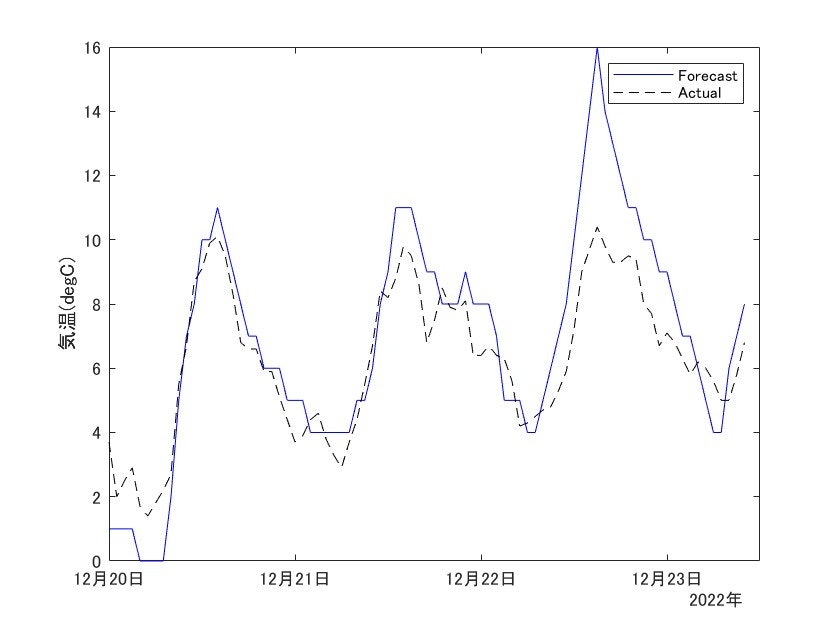
上図は予報値に実績値を黒の破線で重ね書きしています。
12月21日まではそこそこあっているものの、22日はかなり外れています。
ご存知の通り、この週の後半では寒気が流れ込んで、日本海側などでは豪雪による被害が出ていました。
関東も降雪は少なかったものの、気温がかなり落ちました。
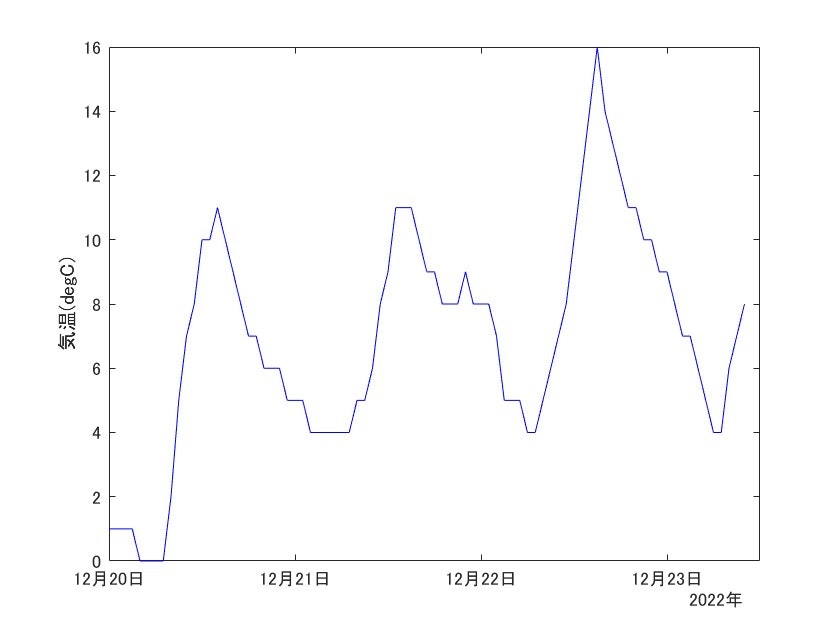
それを確かめるために、予報に使った気温データに対し、実際の気温をプロットして確認してみます。

上図において、青が予測に使用した気温データ、黒の破線が実際の気温です。
見ての通り、22日の気温が予測に対し、最大6degC程度の誤差があることが分かります。
予報では季節外れに暖かくなると予測していました。

では、この実際の気温のデータを使ってみた場合での需要の予測精度がどうなるかを最後に見てみます。

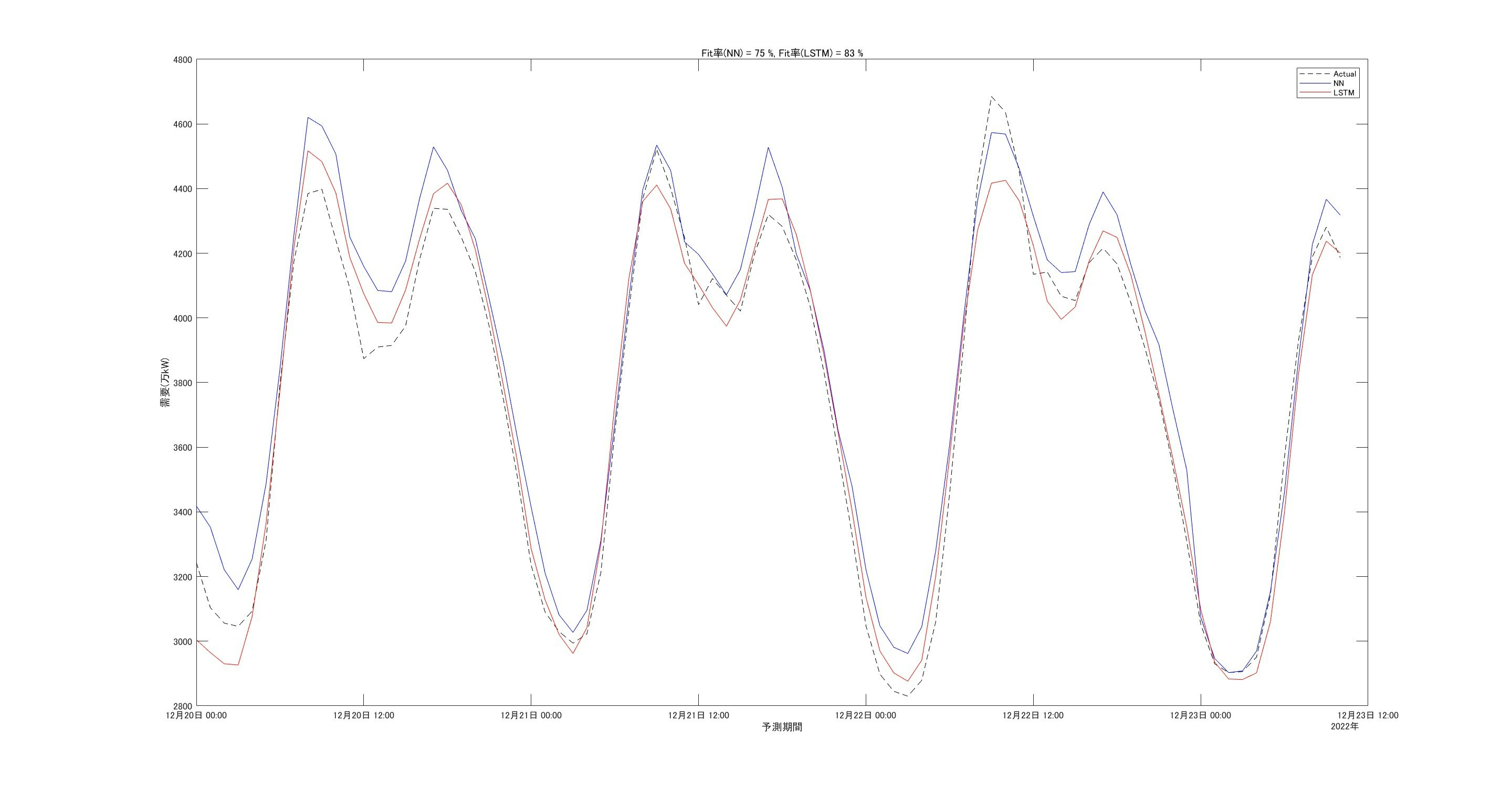
LSTMのFit率が大きく改善しているのが分かります。
特に22日の値について、9時ごろに記録する需要ピーク（4685万kW）は捉えられないものの、夕刻以降のトレンドはそこそこ良い感じです。
ちなみに22日のピークは2022年10月以降で今現在における最大の需要値のようです。（下図青線）
やはり、異常な寒気の影響を受けて暖房需要が伸びているのでしょうか。

このように需要予測を行う場合、入力データにも予報データが入ってくるケースがあります。
スパコンによる気象モデルの計算などによって予報値の精度は段々と上がってきているようですが、それでも2，3日先の予測になってくると不確実性は増していきます。
需要予測の難しさが垣間見れます。