はじめに
重回帰分析の発展として正則化について勉強しました。今回はラッソ回帰(L1正則化)についてまとめています。重回帰分析については下記記事にまとめているので興味ある方はご確認いただければと思います。
参考
ラッソ回帰(L1正則化)の理解に当たって下記を参考にさせていただきました。
- 機械学習のエッセンス 加藤公一(著) 出版社; SBクリエイティブ株式会社
- 正則化の種類と目的 L1正則化 L2正則化について
- リッジ回帰とラッソ回帰の理論と実装を初めから丁寧に
- L1正則化(Lasso)の数式の解説とスクラッチ実装
- [ラッソ回帰を実装してみよう]
(https://qiita.com/NNNiNiNNN/items/75b263298e6a112d5929)
ラッソ回帰(L1正則化)概要
重回帰分析の復習
ラッソ回帰は重回帰分析を行う際の損失関数に対して正則化項を付与したものになります。
重回帰分析は下記のような損失関数を最小化する重みを見つけることで、最適な回帰式を導きだします。
$$L = \sum_{n=1}^{n} (y_{n} -\hat{y}_{n} )^2$$
- $y_{n}$は実測値
- $\hat{y}_{n}$の予測値
ベクトルの形式で表現するとこのような感じになります。
$$L = (\boldsymbol{y}-X\boldsymbol{w})^T(\boldsymbol{y}-X\boldsymbol{w})$$
- $\boldsymbol{y}$は目的変数の実測値をベクトル化したもの
- $\boldsymbol{w}$は重回帰式を作成した際の回帰係数をベクトル化したもの
- $X$はサンプル数$n$個、変数の数$m$個の説明変数の実測値を行列化したもの
上記$L$を最小化するような重み$\boldsymbol{w}$が求められればOKです。
上記$L$を$\boldsymbol{w}$で微分して$0$と置くと下記のようになります。
$$X^T\boldsymbol{y}-X^TX\boldsymbol{w} = 0$$
こちらを解くことで重み$\boldsymbol{w}$を求めることができます。
ラッソ回帰(L1正則化)
$$L = \dfrac {1}{2}(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) + \lambda|| \boldsymbol{w} ||_{1}$$
上記がラッソ回帰(L1正則化)の損失関数の式になります。重回帰分析の損失関数に正則化項 $\lambda|| \boldsymbol{w} ||_{1} $を付け足した形になっています。
ラッソ回帰(L1正則化)では上記のように重み$\boldsymbol{w}$のL1ノルムを加えることで正則化行います。
L1ノルムとは何か
ベクトル成分の絶対値の和(マンハッタン距離と呼ばれる)がL1ノルムです。ノルムは「大きさ」を表す指標で他にL1ノルムやL∞ノルムなどが使われます。
L1正則化の効果
L1正則化項を損失関数に加えることで重み$\boldsymbol{w}$の値を0へと誘導します。
その結果、余計な説明変数(特徴量)をモデルから省く次元圧縮的な効果があります。
通常の重回帰分析の場合、最小化する項は下記のみです。
$$(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})$$
こちらに正則化を加えると、下記項も含めて最小化を行う必要があります。
$$\lambda|| \boldsymbol{w} ||_{1}$$
重み$\boldsymbol{w}$の絶対値の和を損失関数に加えているため、その損失関数の最小化に向けて値が0になる重み$\boldsymbol{w}$をできるだけ増やす方向に進んでいきます。また$\lambda$の大きさによってその度合いをコントロールしています。
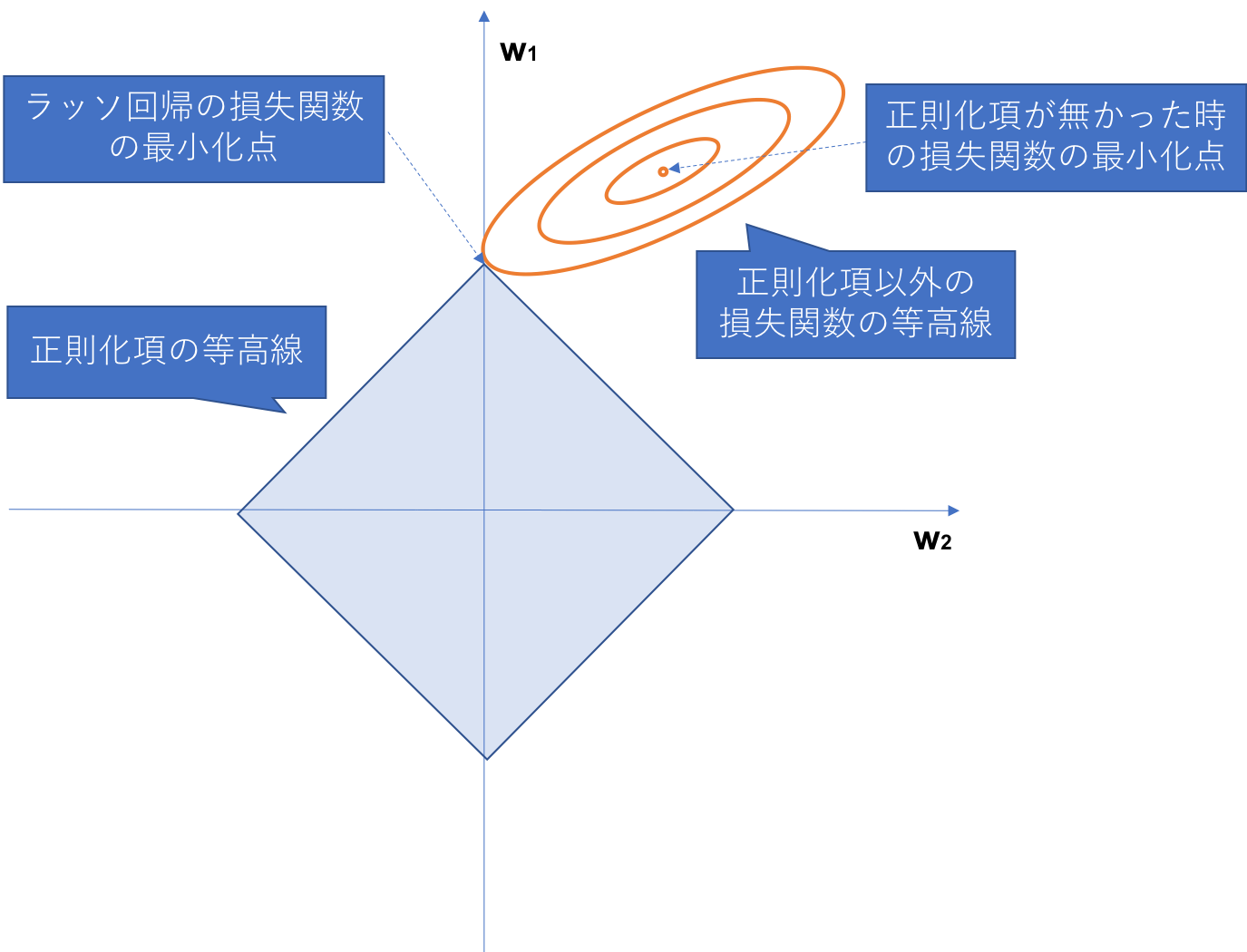
ラッソ回帰(L1正則化)の説明として下記のような図がよく用いられます。
そのままだとわかりにくいため図の中で説明を加えています。下記は重みのパラメーターが2種類だった時の損失関数の値の等高線を2次元上にプロットしたものになります。正則化項を加えることで重みの値が0となっていく様子が図上でわかるかと思います。
ラッソ回帰(L1正則化)の重みの導出
$$L = \dfrac {1}{2}(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) + \lambda|| \boldsymbol{w} ||_{1}$$
上記損失関数を最小化するのが解くべきタスクなのですが、ラッソ回帰の損失関数は普通の重回帰やリッジ回帰と異なり一気に微分して解析的に解くということができません。(L1正則化項が絶対値の和となっているため、そのままでは微分ができない。)
従って場合分けをしながら、右微分や左微分といった方法を駆使して最適な重みの導出を目指します。
ちなみに1/2については偏微分した時の式がすっきりするので付与しているイメージです。
最適な重みを導出するためのラッソ回帰のアルゴリズムは複数ありますが、今回は**座標降下法(coordinate descent)**用いて重みの導出を目指します。座標降下法は重みを1つずつ更新する操作を繰り返して最適解に近似させる方法です。
複数の重み$w_{0},w_{1},w_{2},...w_{k}$があるとすると、一度に全ての重みを更新するのではなく重みを1つずつ順番に更新します。
ラッソ回帰(L1正則化)の重みの導出計算
重みの導出計算方法について数式を追っていきたいと思います。
まずは、回帰式の中に登場する変数を下記とおきます。
\begin{split}\begin{aligned}
\boldsymbol{y}=
\begin{bmatrix}
y_{1} \\
y_{2} \\
\vdots \\
y_{j}
\end{bmatrix} \\
\end{aligned}\end{split}
\begin{split}\begin{aligned}
\boldsymbol{\hat{y}}=
\begin{bmatrix}
\hat{y}_{1} \\
\hat{y}_{2} \\
\vdots \\
\hat{y}_{j}
\end{bmatrix} \\
\end{aligned}\end{split}
\begin{split}\begin{aligned}
\boldsymbol{w}=
\begin{bmatrix}
w_{0} \\
w_{1} \\
\vdots \\
w_{i}
\end{bmatrix} \\
\end{aligned}\end{split}
\begin{split}\begin{aligned}
X=
\begin{bmatrix}
1 & x_{11} & x_{12} & \cdots & x_{1i} \\
1 & x_{21} & x_{22} & \cdots & x_{2i} \\
\vdots \\
1 & x_{j1} & x_{j2} & \cdots & x_{ji}
\end{bmatrix} \\
\end{aligned}\end{split}
$X$の1列目はバイアスである$w_{0}$に対応しています。
$w_{0}$は正則化項には含まれないため、重みを導出する際に別個で計算します。
バイアスの更新式
まずは$w_{0}$の更新式を考えます。
$w_{0}$は正則化項に含まれないためそれ以外の部分のみを考慮します。
$$L = \dfrac {1}{2}(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})$$
こちらを$\boldsymbol{w}$で偏微分すると下記のような式になります。
\begin{eqnarray}
\dfrac {\partial L}{\partial w}&=&X^{T}Xw-X^{T}y \\
&=&X^{T}(Xw-y)
\end{eqnarray}
損失関数$L$を偏微分した式は下記のようになるため、
$\dfrac {\partial L}{\partial w_{0}}$に対応する1行目がどのようになっているかをまずは見ていきます。
{\dfrac {\partial L}{\partial w}
=
\begin{pmatrix}
\dfrac {\partial L}{\partial w_{0}} \\
\dfrac {\partial L}{\partial w_{1}} \\
\vdots \\
\dfrac {\partial L}{\partial w_{i}} \\
\end{pmatrix}
}
偏微分後の式の中身を見ていきます。
\begin{eqnarray}
\dfrac {\partial L}{\partial w}&=&X^{T}(Xw-y)
\\&=&
\begin{split}\begin{aligned}
\begin{bmatrix}
1 & 1 & \cdots & 1 \\
x_{11} & x_{21} & \cdots & x_{j1} \\
\vdots \\
x_{1i} & x_{2i} & \cdots & x_{ji}
\end{bmatrix}
(
\begin{bmatrix}
1 & x_{11} & \cdots & x_{1i} \\
1 & x_{21} & \cdots & x_{2i} \\
\vdots \\
1 & x_{j1} & \cdots & x_{ji}
\end{bmatrix} \\
\end{aligned}\end{split}
\begin{bmatrix}
w_{0} \\
w_{1} \\
\vdots \\
w_{i}
\end{bmatrix}
-
\begin{bmatrix}
y_{1} \\
y_{2} \\
\vdots \\
y_{j}
\end{bmatrix} \\
)
\\&=&
\begin{bmatrix}
1 & 1 & \cdots & 1 \\
x_{11} & x_{21} & \cdots & x_{j1} \\
\vdots \\
x_{1i} & x_{2i} & \cdots & x_{ji}
\end{bmatrix}
\begin{bmatrix}
w_{0} + w_{1}x_{11} + \cdots + w_{i}x_{1i}-y_{1} \\
w_{0}+ w_{1}x_{21} + \cdots + w_{i}x_{2i}-y_{2} \\
\vdots \\
w_{0} + w_{1}x_{j1} + \cdots + w_{i}x_{ji}-y_{j}
\end{bmatrix} \\
\end{eqnarray}
ここで、結果の1行目だけに着目すると以下のようになります。
\begin{eqnarray}
\dfrac {\partial L}{\partial w_{0}}&=& (w_{0} + w_{1}x_{11} + \cdots + w_{i}x_{1i}-y_{1}) + (w_{0} + w_{1}x_{21} + \cdots + w_{i}x_{2i}-y_{2} )+ \cdots +(w_{0} + w_{1}x_{j1} + \cdots + w_{i}x_{ji}-y_{j}) \\
&=& j・w_{0}+\sum_{k=1}^{j}\sum_{l=1}^{i}w_{k}x_{kl}-\sum_{k=1}^{j}y_{k}
\end{eqnarray}
こちらを$0$と置いて$w_{0}$について解きます。
w_{0}=\frac{1}{j}\sum_{k=1}^{j}(y_{k}-\sum_{l=1}^{i}w_{k}x_{kl})
上記の式が**バイアス($w_{0}$)**の更新式となります。
重みの更新式
それでは残りの重み$w_{k}$の更新式について考えていきます。
$$L = \dfrac {1}{2}(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})+ \lambda|| \boldsymbol{w} ||_{1}$$
こちらを$\boldsymbol{w}$で偏微分すると下記のような式になると仮定します。(正則化項が絶対値を含まない場合はこのよう素直に計算できるという、計算上の便宜上の仮定。)
正則化項に絶対値を含むため本来「右偏微分」「左偏微分」というかたちで場合分けが必要となりますが、後ほど符号を変化させることで対応します。
\begin{eqnarray}
\dfrac {\partial L}{\partial w}&=&X^{T}Xw-X^{T}y+\boldsymbol{λ} \\
&=&X^{T}(Xw-y)+\boldsymbol{λ}
\end{eqnarray}
それでは下記式を思い出しつつ、$w_{k}$の重みの更新式を考えていきます。
\begin{eqnarray}
\dfrac {\partial L}{\partial w}&=&X^{T}(Xw-y)
\\&=&
\begin{bmatrix}
1 & 1 & \cdots & 1 \\
x_{11} & x_{21} & \cdots & x_{j1} \\
\vdots \\
x_{1i} & x_{2i} & \cdots & x_{ji}
\end{bmatrix}
\begin{bmatrix}
w_{0} + w_{1}x_{11} + \cdots + w_{i}x_{1i}-y_{1} \\
w_{0}+ w_{1}x_{21} + \cdots + w_{i}x_{2i}-y_{2} \\
\vdots \\
w_{0} + w_{1}x_{j1} + \cdots + w_{i}x_{ji}-y_{j}
\end{bmatrix} \\
\end{eqnarray}
まずは具体的に$w_{1}$の重みの更新式をみてみます。
\begin{eqnarray}
\dfrac {\partial L}{\partial w_{1}}&=& x_{11}(w_{0} + w_{1}x_{11} + \cdots + w_{i}x_{1i}-y_{1}) + x_{21}(w_{0} + w_{i}x_{21} + \cdots + w_{i}x_{2i}-y_{2} )+ \cdots +x_{j1}(w_{0} + w_{1}x_{j1} + \cdots + w_{i}x_{ji}-y_{j})+\lambda \\
&=& w_{1}\sum_{k=1}^{j}x_{k1}^{2}+\sum_{k=1}^{j}x_{k1}(w_{0}+ \sum_{l \neq 1}^{i}w_{l}x_{kl}-y_{k})+ \lambda
\end{eqnarray}
こちらを$0$と置いて$w_{1}$について解きます。
\begin{eqnarray}
w_{1} &=& \frac{\sum_{k=1}^{j}x_{k1}(y_{k} - w_{0} - \sum_{l \neq 1}^{i}w_{l}x_{kl})- \lambda}{\sum_{k=1}^{j}x_{k1}^{2}}
\end{eqnarray}
これは$w_{n}$と置き換えても同様です。
\begin{eqnarray}
w_{n} &=& \frac{\sum_{k=1}^{j}x_{kn}(y_{k} - w_{0} - \sum_{l \neq n}^{i}w_{l}x_{kl})- \lambda}{\sum_{k=1}^{j}x_{kn}^{2}}
\end{eqnarray}
ここで「右偏微分」「左偏微分」の場合わけを行います。
右偏微分の更新式はこのようになります。
\begin{eqnarray}
w_n^+ &=& \frac{\sum_{k=1}^{j}x_{kn}(y_{k} - w_{0} - \sum_{l \neq n}^{i}w_{l}x_{kl})- \lambda}{\sum_{k=1}^{j}x_{kn}^{2}}
\end{eqnarray}
左偏微分の更新式は$\lambda$の符号を反転させたかたちになります。
\begin{eqnarray}
w_n^- &=& \frac{\sum_{k=1}^{j}x_{kn}(y_{k} - w_{0} - \sum_{l \neq n}^{i}w_{l}x_{kl})+ \lambda}{\sum_{k=1}^{j}x_{kn}^{2}}
\end{eqnarray}
重みが更新される条件
上では重み$w_{n}$の符号に応じて更新式の場合分けが発生する旨を記載しました。
$w_n^+$は$w_{n}$が正の値であることを前提に計算されているための下記条件が必要です。
\begin{eqnarray}
w_n^+ &=& \sum_{k=1}^{j}x_{kn}(y_{k} - w_{0} - \sum_{l \neq 1}^{i}w_{l}x_{kl})- \lambda > 0
\end{eqnarray}
また逆に$w_n^-$は$w_{n}$が不の値であることを前提に計算されているため下記条件が必要です。
\begin{eqnarray}
w_n^- &=& \sum_{k=1}^{j}x_{kn}(y_{k} - w_{0} - \sum_{l \neq 1}^{i}w_{l}x_{kl})+ \lambda < 0
\end{eqnarray}
上記2つの条件に当てはまらない下記のような状態の場合、$w_{n}$は初期値$0$のまま留まります。
\begin{eqnarray}
-\lambda ≦ \sum_{k=1}^{j}x_{kn}(y_{k} - w_{0} - \sum_{l \neq 1}^{i}w_{l}x_{kl}) ≦ \lambda
\end{eqnarray}
こちらがラッソ回帰によって重み$\boldsymbol{w}$のパラメータの数を減らすことができるカラクリになります。多くのパラメータが上記範囲に留まることによって$0$となることがわかります。
上記の重みの更新を繰り返し、収束したら更新を止めるかたちになります。
単純に$n$回更新を繰り返すものもあれば、特定の収束条件を定めるものもあるようです。
Next
今回はラッソ回帰の理論について勉強した内容をまとめました。
次回はラッソ回帰を自力実装していきたいと思います。