はじめに
機械学習の分類タスクにはその目的に応じて幾つかの性能評価指標があります。二項分類の評価指標としてはROC曲線やPR曲線のAUC(気曲線の下側面積)が主な手法として存在していますが、その理解の前段としてこの記事では「再現率(Recall-rate)」と「適合率(Precision-rate)」について整理します。
参考
適合率と再現率の理解にあたって下記を参考にさせていただきました。
分類タスク
文書分類タスクの具体例を交えて性能評価方法の説明を行います。その前段としてこの章では分類タスクの実施手法を簡単に記載しますが、分類タスク自体についての記事ではないためモデルの詳細な解説は省いています。
使用したライブラリ
- numpy 1.15.4
- lightgbm 2.3.1
- pandas 0.25.1
- scikit-learn 0.22.2
データセット
今回データセットは「livedoor ニュースコーパス」を使用しています。データセットの詳細やその形態素解析の方法は以前投稿した記事で投稿をご参照ください。
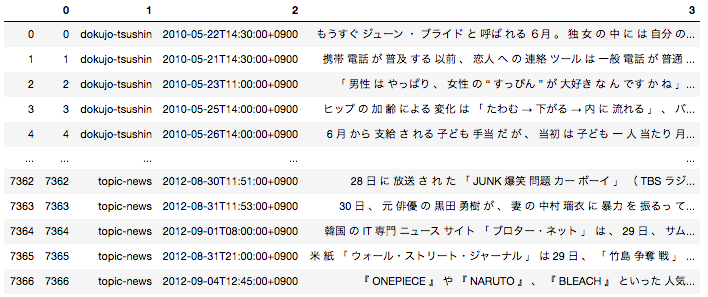
日本語の場合は事前に文章を形態素単位に分解する前処理が必要となるため、全ての文章を形態素に分解した後下記のようなデータフレームに落とし込んでいます。
一番右のカラムが文章を全て形態素解析して半角スペースごとに区切ったものになります。こちらを使用して分類タスクを実施します。
モデルの作成と分類の実施
今回は「Peachy」の記事と「独女通信」の記事(どちらも女性向けの記事)を分類します。今回は二項分類であるため、「独女通信」の記事か否かを判定する分類タスクと同義になっています。データセットを7:3に分割し、7を学習用、3を評価用にしています。
import pandas as pd
import numpy as np
import pickle
from sklearn.feature_extraction.text import TfidfVectorizer
# 形態素分解した後のデータフレームはすでにpickle化して持っている状態を想定
with open('df_wakati.pickle', 'rb') as f:
df = pickle.load(f)
# 今回に2つの種類の記事を分類できるかを検証
ddf = df[(df[1]=='peachy') | (df[1]=='dokujo-tsushin')].reset_index(drop = True)
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(ddf[3])
def convert(x):
if x == 'peachy':
return 0
elif x == 'dokujo-tsushin':
return 1
target = ddf[1].apply(lambda x : convert(x))
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, target, train_size= 0.7, random_state = 0)
import lightgbm as lgb
from sklearn.metrics import classification_report
train_data = lgb.Dataset(X_train, label=y_train)
eval_data = lgb.Dataset(X_test, label=y_test)
params = {
'boosting_type': 'gbdt',
'objective': 'binary',
'random_state':0
}
gbm = lgb.train(
params,
train_data,
valid_sets=eval_data,
)
y_preds = gbm.predict(X_test)
こちらで予測が完了しました。y_predsにはその文書が「独女通信」である確率の値が入っています。
分類性能の評価方法
以下では二項分類タスクの性能評価において重要な考え方を整理していきます。
混合行列
混合行列とは二項分類タスクの出力結果をまとめたマトリクスのことで、二項分類の性能評価に使用します。
| Positiveと予測された | Negativeと予測された | |
|---|---|---|
| 実際にPositiveクラスに属する | TP(真陽性) | FN(偽陰性) |
| 実際にNegativeクラスに属する | FP:(偽陽性) | TN(真陰性) |
**「TP・FP・FN・TN」**それぞれについて言葉で説明すると下記のようになります。この4つの値を使って性能評価をしていくので、非常に重要です。
- TP(真陽性):実際にPositvieだし、分類モデルもPositiveと予測した
- FP(偽陽性):実際はNegativeだが、分類モデルはPositiveと予測した
- FN(偽陰性):実際はPositiveだが、分類モデルはNegativeと予測した
- TN(真陰性):実際にNegativeだし、分類モデルもNegativeと予測した
今回実施した分類タスクに当てはめると下記のようになります。
| 「独女通信」の記事であると予測された | 「独女通信」の記事ではないと予測された(=「Peachy」の記事であるであると予測された) | |
|---|---|---|
| 実際に「独女通信」の記事である | TP(真陽性) | FN(偽陰性) |
| 実際に「独女通信」の記事ではない(=実際には「Peachy」の記事である) | FP:(偽陽性) | TN(真陰性) |
sklearnを使ってこのマトリクスは簡単に作成することができます。
機械学習モデルの予測結果は確率値で出力されているため、一旦ここでは値が$0.5$以上のものを「独女通信」の記事と予測したと考えます。
from sklearn.metrics import confusion_matrix
print(confusion_matrix(y_test, y_preds>0.5))
出力結果はこちら
[[237 11]
[ 15 251]]
上記の表に当てはめるとこのようになります。TPとTNの数が多いので何となく性能が良さそうであることは分かります。この値を使って再現率と適合率について見ていきます。
| 「独女通信」の記事であると予測された | 「独女通信」の記事ではないと予測された(=「Peachy」であると予測された) | |
|---|---|---|
| 実際に「独女通信」の記事である | 237(TP) | 11(FN) |
| 実際に「独女通信」の記事ではない(=実際には「Peachy」の記事である) | 15(FP) | 251(TN) |
再現率(Recall)
\text{recall} = \frac{TP}{TP + FN}
上記の式が**再現率(Recall)**を求める式になります。**感度(sensitivity)や真陽性率(true positive rate:TPR)**とも呼ばれます。今回の具体例を当てはめると下記のようになります。
{{\begin{eqnarray*}
\text{recall} &=& \frac{分類モデルが「独女通信」の記事であると予測した結果が正解であった件数}{実際の「独女通信」の記事の全件数} \\
&=& \frac{237}{237+11} \\
&\simeq& 96\%
\end{eqnarray*}}}
再現率は見つけたいデータ(今回の場合だと「独女通信」の記事)の内その分類器がどの程度の割合を見つけることができるか、を示します。網羅性を測る指標と言い換えられます。
一方でこの指標の弱点はどの程度の誤分類をしているのかがわからない点です。極端な例をあげると、今回の分類モデルが全ての文章を「独女通信」の記事であると予測した場合、再現率は$100%$になってしまいます。それによって「独女通信」の記事を全て網羅することができてしまうからです。従って、性能を測るには次に紹介する適合率と合わせて見ていくことが必須です。
また今回は分類モデルの出力結果が$0.5$以上のものを「独女通信」の記事であると分類しましたが、$0.5$という閾値は不変のものではありません。時には適切なものに変化させていくことが必要です。
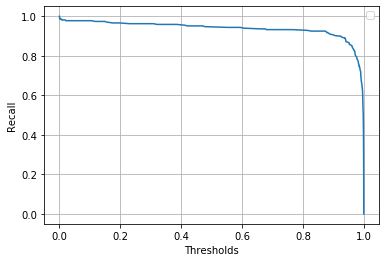
y軸に再現率をx軸に閾値を取ったグラフを確認します。
import matplotlib.pyplot as plt
from sklearn import metrics
precision, recall, thresholds = metrics.precision_recall_curve(y_test, y_preds)
plt.plot(np.append(thresholds, 1), recall)
plt.legend()
plt.xlabel('Thresholds')
plt.ylabel('Recall')
plt.grid(True)
閾値は低く設定した方が再現率は高くなること明らかだと思います。一方で誤分類が多くなってしまうので、閾値も次に紹介する適合率との関係を見ながら適切なものを設定する必要があります。
適合率(Precicsion)
\text{precision} = \frac{TP}{TP + FP}
上記が**適合率(Precision)**を求める式になります。今回の具体例に当てはめると下記のようになります。
{{\begin{eqnarray*}
\text{recall} &=& \frac{分類モデルが「独女通信」の記事であると予測した結果が正解であった件数}{分類モデルが「独女通信」の記事であると予測した全件数} \\
&=& \frac{237}{237+15} \\
&\simeq& 94\%
\end{eqnarray*}}}
適合率は分類器が"これが見つけたいデータである(今回の場合は「独女通信の記事」)"と判断したデータの内、本当に見つけたいデータの割合はどの程度であるか、を示します。分類器がPositiveと判断した時のその判断の確からしさを表している、と言い換えられます。(Negativeと判断した時の確からしさは無視していることに注意)
一方でこの指標の弱点はNegativeの判断はどの程度間違っているか全く分からない点です。例えば、この分類器が1件だけを「独女通信」の記事であると予測して、それが正解であれば適合率は$100%$になってしまいます。この場合は「独女通信」ではないと判断した記事の中に、多くの本当は「独女通信」の記事であるものが含まれてしまいます。
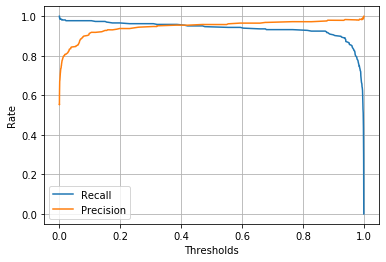
従って、この適合率もまた再現率と一緒に見ることが必須です。ただ、**再現率と適合率はトレードオフの関係になっています。**先ほどの閾値と再現率のグラフに適合率のグラフも重ねて確認します。
import matplotlib.pyplot as plt
from sklearn import metrics
precision, recall, thresholds = metrics.precision_recall_curve(y_test, y_preds)
plt.plot(np.append(thresholds, 1), recall, label = 'Recall')
plt.plot(np.append(thresholds, 1), precision, label = 'Precision')
plt.legend()
plt.xlabel('Thresholds')
plt.ylabel('Rate')
plt.grid(True)
閾値が小さく再現率が高い時は適合率が低く、閾値が大きくて適合率が高い時は再現率が低い、という関係になっています。タスクの目的を鑑みながら、どちらをより重視するかを考え、閾値を設定する必要があります。
F値(F1-score)
再現率と適合率を合わせて性能を測る手法として**F値(F1-score)**があります。F値は再現率と適合率の調和平均にあたり、下記のような式で表されます。
{{\begin{eqnarray*}
F_{1} &=& \frac{2}{\frac{1}{\text{recall}} + \frac{1}{\text{precision}}} \\
&=& 2\times\frac{\text{recall}\times\text{precision}}{\text{recall}+\text{precision}}
\end{eqnarray*}}}
今回の分類タスク(閾値は$0.5$)のF値を求めると下記のようになります。
{{\begin{eqnarray*}
F_{1} &=& \frac{2}{\frac{1}{0.96} + \frac{1}{0.94}} \\
&\simeq& 0.95
\end{eqnarray*}}}
非常に精度が良い分類を行なっていると言えそうです。F値は適合率と再現率が同じように高い分類器を高く評価しますが、常にそれが望ましいというわけではありません。適合率の方が重視される場合や再現率の方が重視される場合もあるので、分類の目的に応じて性能評価の指標を使い分けることが必要です。
Next
次回はROC曲線やPR曲線についてまとめたいと考えています。