dbtのPython modelを使って、RSA暗号を攻撃

1.　イントロダクション

dbtのPython modelを用いて、RSA暗号を攻撃して遊んでみました。

2.　モチベーション

最近使ってるdbtと最近知った暗号の知識使って、遊んでみたかったためです。

3.　動作環境

% dbt --version
Core:
  - installed: 1.3.1
  - latest:    1.3.1 - Up to date!

Plugins:
  - snowflake: 1.3.0 - Up to date!

4.　環境準備

色々チュートリアルがありますが、例えばAccelerating Data Teams with dbt Core & Snowflakeを参考にしました。

5.　やったこと

dbtのPython modelを使って、RSA暗号をWiener's attackという手法で攻撃してみました。

6.　事前知識

dbtのPython modelを使って、実際にRSA暗号を攻撃する実装を行う前に、簡易的な事前知識を書きます。

6-1.　dbt

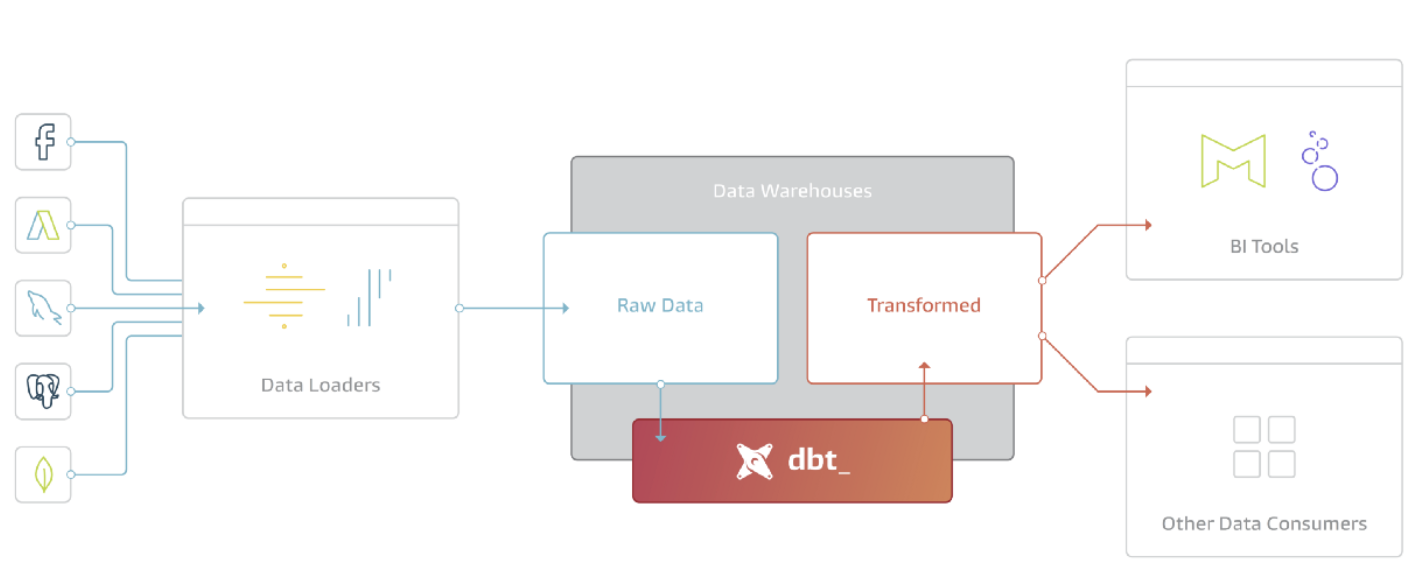
dbt（Data Build Tool）とは、dbt Labs社が開発している、ストレージから取り出したデータをデータウェアハウスへ適した変換をする処理の工程である、ELT（Extract、Load、Transform）の「T（Transform）」を担うツールになります。

6-2.　RSA暗号

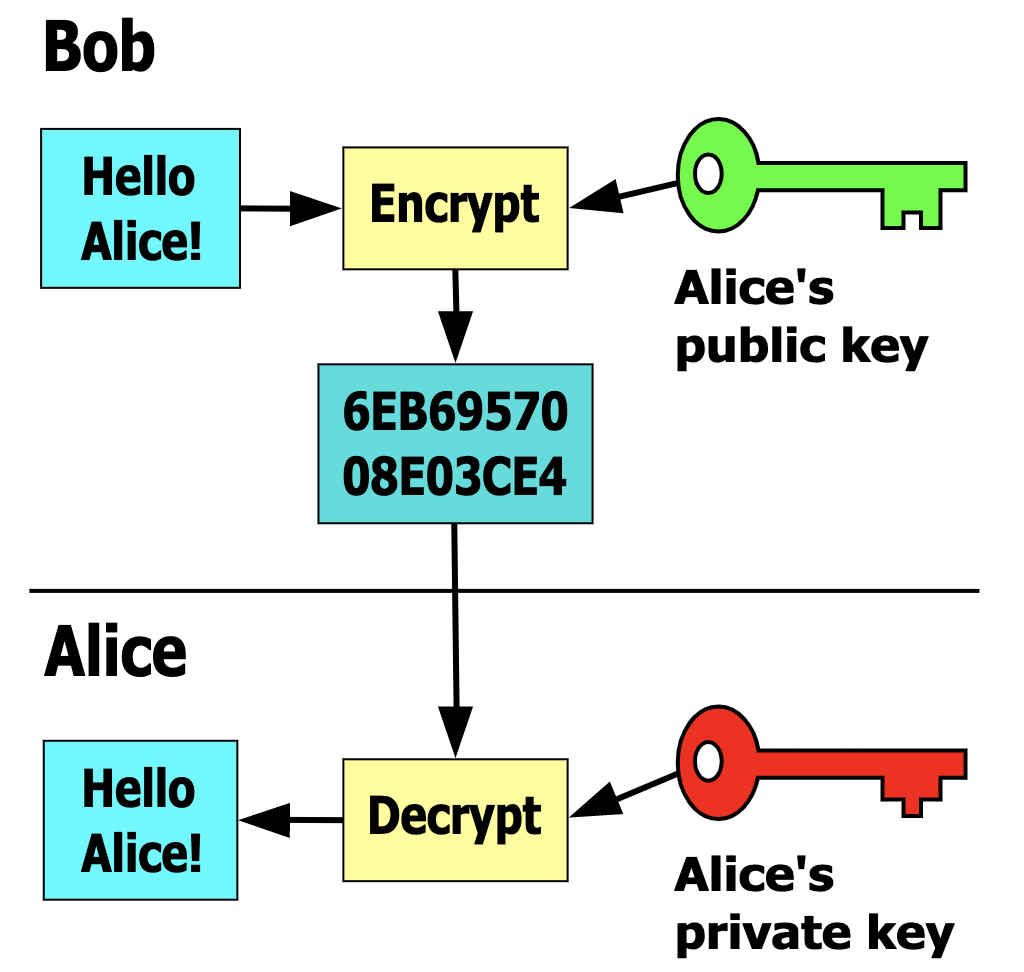
RSA（Ronald Linn Rivest・Adi Shamir・Leonard Max Adleman）暗号は公開鍵暗号の一つです。通信を受ける者（受信者：Alice）は鍵のペア（公開鍵と秘密鍵）を作成して公開鍵を公開します。暗号通信をしたい者（送信者：Bob）は公開鍵を用いてメッセージを暗号化してから送信した後、Aliceは自身の秘密鍵（復号のための鍵）を使って受信内容を復号し、Bobからのメッセージを解読します。

RSA暗号における、暗号化および復号化の手順は以下になります。

(1) Aliceは２つの大きな素数$\{p,q\}$を生成します。簡易的な例でイメージがつきやすいよう、ここでは$\{p=11,q=15\}$とします。

(2) Aliceは２つの大きな素数を掛け合わせ$N$を作ります。ここでは$N = p \times q = 165$になります。さらに、$ (p-1)(q-1)$と互いに素になるような数$e$を選びます。このときは$e = 3$と選びます。

(3) Aliceは$\{N,e\}$のペアを公開します。これら2つの数はAliceへ暗号化されたメッセージを送りたい人なら誰でもみられるようにする必要があります。そして、$\{N,e\}$は公開鍵と呼ばれます。

(4) Bobがメッセージを暗号化する前に、メッセージを数値$M$に変換する必要があります。ここでは、一つの文字をASCIIの二進数に変換し、その二進数を十進数に置き換えます。その置き換えられた$M$は以下の式に従って暗号化され、その暗号文の数値を$C$とします。中国の剰余定理により、$p$と$q$が互いに素であることで、$0 \leq C < N$を満たす$C$が一意的に定まります。

C = M^{e}\, (\mathrm{mod}\, N)

(5) 例えば、ボブがアリスに$T$という文字を送るとします。ASCIIでは$T$は1010100で表され、$M$は十進数の84になります。与えられた$\{N,e\}$と$M$を使って、暗号化すると

\begin{align}
C &= 84^{3}\, (\mathrm{mod}\, 165) \\
  &= [84^{2}\, (\mathrm{mod}\, 165) \times 84\, (\mathrm{mod}\, 165)]\, (\mathrm{mod}\, 165) \\
  &\equiv 24　\, (\mathrm{mod}\, 165)
\end{align}

となり、Bobは24という暗号文をAliceに送ります。

(6) 盗聴者（Eve）は24という暗号文を見ることになりますが、Eveが暗号文$C$を解読するには、3乗された何らかの数$M$を165で割ると余りが24になるような、$M$を探し求めなければならないです。$M^{3}$は少なくても24よりは大きいので、$M=3, 4, 5, \cdots$と探していくと以下の表になります。

$M$	3	4	5	6	$\cdots$
$M^{3}$	27	64	124	216	$\cdots$
$M^{3} (\mathrm{mod}\ 165)$	27	64	124	51	$\cdots$

この表を見てみると、$M^{3} (\mathrm{mod}\ 165)$の値は規則性が分かりづらいのは見て取れます。したがって、24となるような数$M$を探すのは骨が折れそうです。今回は$\{N=165,e=3 \}$としていますが、実際はそれ以上に$\{N,e \}$は大きいので、Eveが暗号文を$\{N,e \}$と$C$から愚直に探すのは困難と言えます。しかし、Aliceは自分の秘密鍵を使う鍵を使うことで、$\{N,e \}$と$C$から用意に復号化できます。

(7) $C$の復号化の前に、Aliceは用意していた２つの素数$\{p=11,q=15 \}$で、秘密鍵$d$を作る必要があります。$d$の作り方は以下に従います。$(p-1)(q-1)$としていることで、フェルマーの小定理より復号化できます。

\begin{align}
e \times d \equiv 1 \,[\mathrm{mod}\, (p-1)\times(q-1)]
\end{align}

今回の場合では

\begin{align}
&3 \times d \equiv 1 \,(\mathrm{mod}\, 10\times14) \\ 
\therefore \ &3 \times d \equiv 1 \,(\mathrm{mod}\, 140)　\\
\therefore \ &3d = 140x+1（xは整数） \\
\therefore \ &3d - 140x= 1
\end{align}

となります。ここで、Aliceはユークリッドの互除法を使うことで、容易に$d$を作ることができます。

\begin{align}
&\begin{cases}
3 = 140 \cdot 0 + 3 \\
140 = 3 \cdot 46 + 2 \\
3 = 2 \cdot 1 + 1
\end{cases} \\
\therefore & \ 3 = (140 - 3 \cdot 46) \cdot 1 + 1 \\
\therefore & \ d = 47
\end{align}

(8) Aliceは作成した秘密鍵$d$を使って、暗号文を複合するときは以下の式に従います。

M = C^{d}\, (\mathrm{mod}\, N)

今回の場合、

\begin{align}
M &= 24^{47}\, (\mathrm{mod}\, 165) \\
  &= [24^{1}\, (\mathrm{mod}\, 165) \times 24^{4}\, (\mathrm{mod}\, 165) \times 24^{4 \cdot 11}\, (\mathrm{mod}\, 165) ]\, (\mathrm{mod}\, 165) \\
  &\equiv 84　\, (\mathrm{mod}\, 165)
\end{align}

となり、十進数で84は$T$という文字になるので、無事復号化出来ました。RSA暗号は$N$は公開しますが、$\{p,q \}$は公開しないかつ、余りを求めるようなモジュロ演算による一方向関数を用いているというのが肝です。$\{p,q \}$から$N$作るのは容易で、逆の$N$から素因数分解して$\{p,q \}$を探し求めるのが困難であることが背景にあります。そして、$\{p,q \}$を探し求めず、直接解読するにしても、一方向関数のおかげで、簡単には解読できないようになっています。

6-3.　RSA暗号の攻撃手法

盗聴者（Eve）が暗号を攻撃するということは一般的に復号化の鍵を探し求めることになります。シーザー暗号でしたら何文字分シフトしたかが鍵になり、その鍵を探し求めます。今回のRSA暗号でしたら秘密鍵$d$を探し求めることになります。そして、RSAの攻撃手法は複数あり、その中で、Wiener's attackという手法を使って攻撃しました。Wiener's attackは秘密鍵$d$が小さいとき（$d < \frac{1}{3}N^{\frac{1}{4}}$を満たすとき）、$\{N,e\}$から$d$を求める手法です。
$\phi(p-1,q-1)$を$(p-1)(q-1)$の最小公倍数、$k$を整数とすると、$\phi(p-1,q-1)$も$e$と互いに素になり、復号化も出来るので、$d$の生成は以下のように書き変えられます。

\begin{align}
&ed \equiv 1 \,[ \phi(p-1,q-1)]　　\\
\therefore \ &ed = k\phi(p-1,q-1) + 1 \\
\end{align}

$g$を$\phi(p-1,q-1)$の最大公約数とすると、

\begin{align}
ed &= k\phi(p-1,q-1) + 1 \\
&= \frac{k}{g}(p-1)(q-1) + 1 \\
\therefore \ \frac{e}{N} &= \frac{k}{dg}(1 - \delta),  \; \; \mathrm{where} \; \; \delta = \frac{p+q-1-\frac{g}{k}}{N}\geq 0
\end{align}

となります。ここで現れた$k$と$dg$は、$\delta$が十分小さければ、次のような連分数展開を用いたアルゴリズムを用いることで、$d$を求めることができます。連分数展開を用いたアルゴリズムを以下のステップに分けます。

(1)　$e$を$N$で割ったものを、ユークリッドの互除法に従い、最大公約数が見つかるまで連分数展開します。例えば、$e$を$N$で割ったときの商を$q_{0}$、余りを$r_{0}$として、展開していくと

\begin{align}
&\begin{cases}
e &= q_{0}N + r_{0} \\
N &= q_{1}r_{0} + r_{1} \\
\end{cases} \\
\therefore &
\begin{cases} 
\frac{e}{N} &= q_{0} + \frac{r_{0}}{N} \\
\frac{N}{r_{0}} &= q_{1} + \frac{r_{1}}{r_{0}}\\
\end{cases} \\ 
\therefore \, &\frac{e}{N} = q_{0} + \frac{1}{q_{1} + \frac{r_{1}}{r_{0}}}
\end{align}

となります。$m$番目で最大公約数が見つかったとすると、$e$を$N$で割ったときの連分数展開は以下になります。

\begin{align}
q_{0}&=\lfloor \frac{e}{N} \rfloor, \; r_{0}= \frac{e}{N} - q_{0} \; \; \mathrm{and} \\
q_{i}&=\lfloor \frac{1}{r_{i-1}} \rfloor, \; r_{i}=\frac{1}{r_{i-1}}- q_{i} \; \;(i=1,2,3,\cdots,m)
\end{align}

ここで、$e$を$N$で割ったときの連分数展開の表記を次のように定義します。

\frac{e}{N}= <q_{0},q_{1},q_{2},\cdots,q_{m}>=:f

すると、$i$番目までの連分数展開によって得られた分母と分子を$d_{i}$と$n_{i}(i=1,2,\cdots,m)$とすると、

<q_{0},q_{1},q_{2},\cdots,q_{i}>=\frac{n_{i}}{d_{i}}, \; \; \mathrm{gcd}(n_{i},d{i})=1

となり（$\mathrm{gcd:greatest common divisor}$）、を$d_{i}$と$m_{i}$は以下の漸化式で表せます。

\begin{align}
n_{0}&=q_{0}, \; \; d_{0}=1  \\
n_{1}&=q_{0}q_{1}+1, \; \; d_{1}=q_{1}  \\
n_{i}&=q_{i}n_{i-1}+n_{i-2}, \; \; d_{i}=q_{i}d_{i-1}+d_{i-2} \; \;(i=2,3,\cdots,m)
\end{align}

(2)　そして、$d$を求めるために、連分数展開によって得られた$n_{i}$と$d_{i}$を$k/dg$に近づけていきます。 近づける際、連分数展開の、$j=0,1,2,\cdots,m$として、$q_{j}+1$としたとき、$j$が偶数のとき$f$は単調増加、奇数のときは単調減少になる性質を利用します。$\delta \geq 0$より、$f$は$k/dg$より小さいため、$f$は増加する必要があります。よって、

\begin{align}
\mathrm{for}& \; j=0,1,\cdots,m &\\
&\cdot \begin{cases}
f=<q_{0},q_{1},q_{2},\cdots,q_{j}+1>\;(jは偶数) \\
f=<q_{0},q_{1},q_{2},\cdots,q_{j}>\;(jは奇数)　
\end{cases} \\
&\cdot 増加したfが\frac{k}{dg}と等しいかチェック \\
\mathrm{end}&\mathrm{for}
\end{align}

ここで、$f$を増加させ$k/dg$と等しくなったとき、つまり、$\delta$が十分小さくなったときの$\delta$が満たす範囲として、以下が成り立つ必要があります。

\begin{align}
&\delta　< \frac{1}{\frac{3}{2}n_{m}d_{m}} \\
\therefore \; &\frac{p+q-1-\frac{g}{k}}{N} < \frac{1}{\frac{3}{2}kdg}
\end{align}

$-1-g/k$は$p+q$に比べて小さいとみなせるので、

\begin{align}
&\frac{p+q}{N} < \frac{1}{\frac{3}{2}kdg} \\
\therefore \; &kdg < \frac{N}{\frac{3}{2}(p+q)}
\end{align}

となり、これが連分数展開における$k$と$dg$が許される範囲になります。

(3)　増加した$f$が$k/dg$と等しいかチェックでは、$f$から出力された分母と分子を$\tilde{dg}$と$\tilde{k}$として、再度$d$の生成式に戻り、出力結果を元にした$(p-1)(q-1)$と$g$を、$(\tilde{p}-1)(\tilde{q}-1)$と$\tilde{g}$とすると、

\begin{align}
&e\tilde{dg} = \tilde{k}(\tilde{p}-1)(\tilde{q}-1) + \tilde{g} \\
\therefore& \; \frac{e\tilde{dg}}{\tilde{k}} = (\tilde{p}-1)(\tilde{q}-1) + \frac{\tilde{g}}{\tilde{k}}
\end{align}

となります。もしここで、$(\tilde{p}-1)(\tilde{q}-1)$が0であったら、$\tilde{dg}$と$\tilde{k}$は間違った出力結果になります。この$e\tilde{dg}/\tilde{k}$の商の部分$(\tilde{p}-1)(\tilde{q}-1)$に着目して、与えられた$N$を用いて以下の計算を行うと、

\begin{align}
\frac{N-(\tilde{p}-1)(\tilde{q}-1)+1}{2} = \frac{pq-\tilde{p}\tilde{q}+\tilde{p}+\tilde{q}}{2}
\end{align}

もし、与えられた$N$と予測している$\tilde{p}\tilde{q}$が一致している場合、上の式は

\begin{align}
\frac{N-(\tilde{p}-1)(\tilde{q}-1)+1}{2} = \frac{\tilde{p}+\tilde{q}}{2}
\end{align}

となります。そして、ゴールドバッハの予想が成り立つと仮定して、$\tilde{p}+\tilde{q}$が2の倍数でなければ、$\tilde{dg}$と$\tilde{k}$は間違った出力結果になります。したがって、$\tilde{p}+\tilde{q}$が2で割り切れるかチェックする必要があります。加えて、与えられた$N$と予測している$\tilde{p}\tilde{q}$が一致している場合、以下の計算も成り立ちます。

\begin{align}
\bigl(\frac{\tilde{p}+\tilde{q}}{2}\bigr)^2 - N = \bigl(\frac{\tilde{p}-\tilde{q}}{2}\bigr)^2
\end{align}

つまり、$(\tilde{p}-\tilde{q})/2$の2乗でなければいけません。つまり、チェックすることは

\begin{align}
\mathrm{for}& \; j=0,1,\cdots,m &\\
&\cdot \begin{cases}
f=<q_{0},q_{1},q_{2},\cdots,q_{j}+1>\;(jは偶数) \\
f=<q_{0},q_{1},q_{2},\cdots,q_{j}>\;(jは奇数)　
\end{cases} \\
&\cdot 増加したfが\frac{k}{dg}と等しいかチェック \\
&\rightarrow　\tilde{p}+\tilde{q}が2で割り切れるか　 \mathrm{and} \\
& \;\;\;\;\;\; \bigl(\frac{\tilde{p}+\tilde{q}}{2}\bigr)^2-Nが2乗になっているか　\\
\mathrm{end}&\mathrm{for}
\end{align}

ということになります。そして、チェックが完了したら、予測している$\tilde{dg}/\tilde{g}$をすることで、秘密鍵$\tilde{d}$を得ることができ、Eveは解読を試みます。

(4)　さらに、$d<\frac{1}{3}N^{\frac{1}{4}}$と$q<p<2q$が成り立つとき、$\frac{k}{dg}$は$f$の主近似分数となり、$m$に至らなくても$d$が求めることができます。証明は以下のラグランジュの定理の結果を用います。今回は省略しますが、気になる方は是非トライしてみてください。

\begin{align}
&実数\alpha、自然数p、整数qに対して、 \\
&\;\;\;\; \bigl| \alpha - \frac{p}{q}　\bigr| < \frac{1}{2q^2}を満たすとき、 \\
&\frac{p}{q}は有限で打ち切った\alphaの連分数展開で得られる（主近似分数）。
\end{align}

7.　手順

まずは、Python modelを使って、暗号化します。

models/python/rsa.py

import math
import random 
import pandas as pd

def get_keys(p, q):
    # 公開鍵（N,e）を求める
    N = p * q
    L = (p-1)*(q-1)
    for i in range(L-1,1,-1):
        if math.gcd(i,L) == 1:
            e = i
            # 秘密鍵dを求める（拡張ユークリッドの互除法）
            a = e
            b = L
            x,y,v,w = 1,0,0,1
            while b:
                q = a // b
                x, v = v, x - q*v
                y, w = w, y - q*w
                a, b = b, a%b
            d = x
            # Wiener's attackで解けやすいようなdをあえて選ぶ
            if d > 0 and d < N**(1/4)/3:
                return (N,e),(d)
    return (N,e),(None)

def encrypt(plain_text, public_key):
    # 公開鍵を使って、メッセージの暗号化
    N,e = public_key

    plain_deciNum = [ord(chr) for chr in plain_text]
    encrypted_deci = [pow(deci,e,N) for deci in plain_deciNum]
    # 暗号化された数字がどの文字に対応しているかわかりやすくするため、
    # ハイフンで切り分けている
    encrypted_text = '-'.join(str(de) for de in encrypted_deci)
    return encrypted_text

def decrypt(encrypted_text, public_key, private_key):
    # 公開鍵と個人鍵（秘密鍵）を使って、メッセージの復号化
    N,_ = public_key
    d = private_key
    encrypted_deci = [int(chr) for chr in encrypted_text.split('-')]
    decrypted_deci = [pow(deci,d,N) for deci in encrypted_deci]
    decrypted_text = ''.join(chr(de) for de in decrypted_deci)
    return decrypted_text

def is_prime(N):
    primes = []
    is_prime = [True]*(N+1)
    is_prime[0] = is_prime[1] = False
    for i in range(2,N+1):
        if not is_prime[i]:
            continue
        primes.append(i)
        for j in range(i*i,N+1,i):
            is_prime[j] = False
    return primes

def get_random_pq(i,j):
    # i: iまでの素数、j: j番目からのrandomな素数（i<j）
    primes = is_prime(i)
    n = len(primes)
    p = primes[random.randint(j,n-1)]
    q = primes[random.randint(j,n-1)]
    while p > q:
        p = primes[random.randint(j,n-1)]
    return p,q

def model(dbt, session):
    plain_text_list = ["ponponがpain","うんちぶりぶり","トイレ"]
    public_key_N_list = []
    public_key_e_list = []
    private_key_d_list = []
    encrypted_text_list = []
    decrypted_text_list = []
    for i in range(len(plain_text_list)):
        is_found_d = False
        while not is_found_d:
            # 0 <= m < N = p * qとなるような、pとqを選ぶ。
            p,q = get_random_pq(10000,100)
            public_key, private_key = get_keys(p,q)
            if private_key is not None:
                is_found_d = True
        N,e = public_key
        d = private_key
        plain_text = plain_text_list[i]
        encrypted_text = encrypt(plain_text,(N,e))
        decrypted_text = decrypt(encrypted_text,(N,e),(d))

        public_key_N_list.append(N)
        public_key_e_list.append(e)
        private_key_d_list.append(d)
        encrypted_text_list.append(encrypted_text)
        decrypted_text_list.append(decrypted_text)

    df = pd.DataFrame.from_dict({"PLAIN_TEXT": plain_text_list
                                , "PUBLIC_KEY_N": public_key_N_list
                                , "PUBLIC_KEY_E": public_key_e_list
                                , "PRIVATE_KEY_D": private_key_d_list
                                , "ENCRYPTED_TEXT": encrypted_text_list
                                , "DECRYPTED_TEXT": decrypted_text_list})
    return df

dbt run --select rsaのコマンドを打った後、暗号化・復号化出来ているか確認すると、以下のようになります。

無事に暗号化・復号化出来ていたので、次に公開鍵と暗号化されたメッセージだけのSQLモデルを作成します。

models/sql/message_rsa.sql

select 
    public_key_N
    , public_key_e
    , encrypted_text
from 
    {{ ref('rsa') }}

dbt run --select message_rsaを打った後、確認すると、以下のようになります。

そして、Eveは公開鍵と暗号化されたメッセージだけのSQLモデルのmessage_rsaだけを見て、以下のようなPython modelを使って、攻撃します。

models/python/wiener_attack.py

import math
import pandas as pd

def rational_to_confrac(x,y):
    while x:
        a = y // x
        yield a
        y,x = x,y%x

def confrac_to_rational_iter(confrac):
    n0,d0 = 0,1
    n1,d1 = 1,0
    for q in confrac:
        n = q*n1 + n0
        d = q*d1 + d0
        yield n,d
        n0,d0 = n1,d1
        n1,d1 = n,d

def convergents_from_confrac(confrac):
    # f"=<q_0',q_1',···,q_m'>として、mが偶数のとき、f'は単調増加(奇数のときは単調減少)
    # f'=f(1-δ) < fより、f'を徐々に増加させて、fへ近づける
    n_,d_ = 1,0
    for i,(n,d) in enumerate(confrac_to_rational_iter(confrac)):
        if i % 2 == 0:
            # 定義により、定義により、<q_0,q_1,···,q_m>　-> <q_0,q_1,···,q_m+1>
            # <=> n_m -> n_m+n_(m-1), d_m -> d_m+d_(m-1)
            yield n+n_, d+d_
        else:
            yield n, d
        n_,d_ = n,d

def is_perfect_square(x):
    if x >= 0:
        s = int(math.sqrt(x))
        return  (s*s) == x
    return False


def attack(n,e):
    f_ = rational_to_confrac(n,e)
    for k,dg in convergents_from_confrac(f_):
        edg = e*dg
        phi = edg // k
        s = n - phi + 1
        if s % 2 == 0 and is_perfect_square((s//2)**2-n):
            g = edg - k*phi
            return dg // g
    return None

def decrypt(encrypted_text, public_key, private_key):
    # 公開鍵と個人鍵（秘密鍵）を使って、メッセージの復号化
    N,_ = public_key
    d = private_key

    if d is None:
        return "攻撃失敗"

    encrypted_deci = [int(chr) for chr in encrypted_text.split("-")]
    decrypted_deci = [pow(deci,d,N) for deci in encrypted_deci]
    decrypted_text = ''.join(chr(de) for de in decrypted_deci)

    return decrypted_text

def model(dbt,session):
    # message_rsaは公開鍵と暗号化されたメッセージが入っているテーブル
    df_message_rsa = dbt.ref("message_rsa").toPandas()

    private_key_list = []
    decrypted_text_list = []

    for i in range(len(df_message_rsa)):
        N = int(df_message_rsa["PUBLIC_KEY_N"][i])
        e = int(df_message_rsa["PUBLIC_KEY_E"][i])

        encrypted_text = df_message_rsa["ENCRYPTED_TEXT"][i]

        private_key = attack(N,e)
        public_key = (N,e)
        decrypted_text = decrypt(encrypted_text,public_key,private_key)

        private_key_list.append(private_key)
        decrypted_text_list.append(decrypted_text)

    df = pd.DataFrame.from_dict({"PRIVATE_KEY_D": private_key_list
                                , "DECRYPTED_TEXT": decrypted_text_list})

    return df

dbt run --select wiener_attackを打った後、攻撃出来ているか見てみると、以下のようになります。

無事に解読できています。今回は攻撃が成功しました。

8.　まとめと感想

• dbtのPython modelを使って、RSA暗号を攻撃してみました
• 攻撃によってRSA暗号が解ける場合があります
  • 2乗の判定部分は、モジュロ演算を使えばより高速化できそうです
• 気が向いたら、一般数体篩法（素因数分解のアルゴリズム）を実装してみてみたいと思います

参考文献

• What, exactly, is dbt?
• データ変換処理をモダンな手法で開発できる「dbt」を使ってみた
• 暗号解読〔下〕 サイモン・シン／著 、青木薫／訳
• 公開鍵暗号
• 中国の剰余定理
• フェルマーの小定理
• Python で公開鍵暗号アルゴリズム RSA を実装してみる
• RSAの攻撃手法
• Cryptanalysis of Short RSA Secret Exponents
• Wiener's attack
• pablocelayes/rsa-wiener-attack
• ₍₍ (ง ˘ω˘ )ว ⁾⁾ < 暗号楽しいです
• Wiener's attack 短い秘密鍵のRSA暗号への攻撃
• Wiener’s Attack を実装した
• 実数の有理数近似と連分数展開
• 連分数/ A. Ya. ヒンチン　
• ゴールドバッハの予想
• 平方数かどうかを高速に判定する方法