最近、仕事でPythonを使ってグラフを作ることが増えてきたので、「音もデータエンジニアっぽくいじってみたらどうなるか?」を試してみました。
題材にしたのは、うちのネコのゴロゴロ音と、洗濯機の動作音です。「なんか家電っぽいゴロゴロだな」と感じることがあり、本当に“それっぽい”のかを軽く検証してみます。
この記事でやることはざっくり次の3つです。
- ネコと洗濯機の音声を 16kHz モノラル・RMS 正規化・3秒 にそろえる
- スペクトログラムで、時間×周波数の違いをざっくり眺める
- MFCC+UMAP で、特徴量空間での「近さ」を確認する
こんなことやってみた
ネコのゴロゴロ音と洗濯機の音をスマホで録音し、ローカルの Python から読み込んで遊びました。
今回は Web アプリまでは作らず、あくまで「音をデータとして前処理→可視化するところまで」をゴールにしています。
やったことの流れはこんな感じです。
- mp3 を Audacity で wav に変換
- Python(librosa)で読み込んで、16kHz モノラル化
- RMS 正規化と 3 秒へのトリミング/パディング
- スペクトログラムの描画
- 0.5 秒ごとに区切って MFCC を取り、平均+標準偏差で要約
- UMAP で 2 次元に圧縮して散布図にプロット
コードは全部ローカルで完結するので、実データ(ネコ音・洗濯機音)は公開せず、画像だけ記事に載せる想定です。
前処理の方針
録音条件が違う音をそのまま比べると、マイク位置や録音レベルの差が目立ってしまいます。
そこで、最低限のルールを決めて両方の音声をそろえました。
16kHz モノラル化
- ネコのゴロゴロや洗濯機のモータ音は、主に低〜中域に成分があります。
- 16kHz サンプリングなら、必要なところはだいたいカバーできそう
- 今回は音色比較が目的なのでステレオ情報は捨てて、モノラルに変換しました。
RMS 正規化
- ネコを至近距離で録った音と、少し離れたところから録った洗濯機音では、波形の振幅が全然違います。
- それぞれの音の“平均的な音量”を測ってから、目標の音量に近づくようにボリュームを調整します。
- こうしておくと、スペクトログラムの「明るさ」が録音レベルの違いではなく、周波数分布の違いとして見やすくなります。
3 秒にそろえる
- ネコ音も洗濯機音も、3 秒あればゴロゴロ 1〜2 サイクルや回転パターンがそこそこ入ります。
- 両方とも 3 秒にトリミングして、「同じ長さのスナップショット」を比較できるようにしました。
以降は、この前処理後の3秒音声を使って可視化していきます。
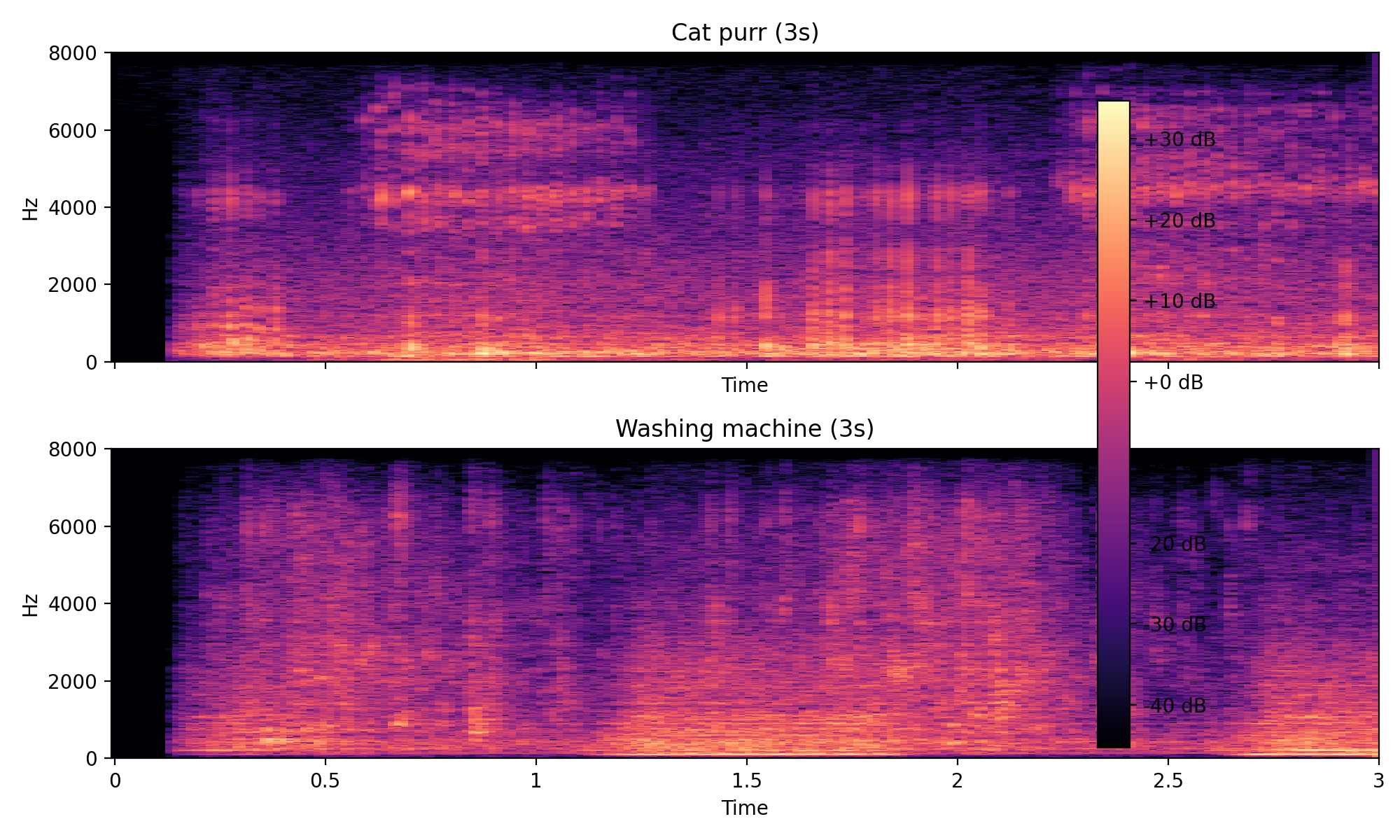
スペクトログラムで見てみる
まずは人間にも直感的なスペクトログラムで、時間×周波数の分布を眺めてみます。
- 横軸:時間(0〜3 秒)
- 縦軸:周波数(0〜8kHz)
- 色 :各時刻×周波数でのエネルギー量(dB)
表示してみると、だいたいこんな傾向が見えました。
-
ネコのゴロゴロ音
- 低〜中域の明るい帯が、時間方向に細かく揺れている。
- 強くなったり弱くなったりする“息づかい”のような変化がある。
-
洗濯機音
- ある程度決まった帯域が、比較的安定して光り続けている。
- モータが一定で回り続けているような「持続的な帯」に見える。
スペクトログラムだけを見ると「性格は違うけれど、どちらも低〜中域にエネルギーが集中している」ことが分かります。
耳で感じていた「家電っぽいゴロゴロ」という印象も、完全に外れてはいなさそうです。
今回使った特徴量(MFCC)
見た目だけでなく、「音を数値にしたときも似ているのか」をざっくり見るために、MFCC を使いました。
MFCC(Mel-Frequency Cepstral Coefficients)は、ざっくり言うと:
- 音を短い時間窓に区切って周波数成分を調べる
- 人間の耳の感じ方に近い「メル尺度」で低音は細かく・高音はざっくりグループ分けする
- いろいろな高さの音の強さを、人間の耳っぽいスケールに直してから、「音色の輪郭」だけを少ない数字に圧縮する
という処理で得られる「音色の指紋」です。
標準的には 13 次元が多いので、この記事でも MFCC 13 次元 を使いました。
0.5 秒ごとに MFCC を要約する
ネコと洗濯機の 3 秒波形を、そのまま 1 サンプルとして扱うと、サンプル数が極端に少なくなります。
そこで、3 秒を 0.5 秒ごと(6 区間) に分けて、それぞれを 1 サンプルとして特徴量を作りました。
1 区間(0.5 秒)については、内部でさらに短いフレームに分けて MFCC を計算したうえで、次のように要約しています。
- 各 MFCC 次元ごとに
- フレーム方向の 平均値(mean)
- フレーム方向の 標準偏差(σ)
- 13 次元 ×(平均+標準偏差)= 26 個の数字
この 26 次元ベクトルを「その 0.5 秒の音の指紋」として使い、ネコと洗濯機それぞれから複数サンプルを作りました。
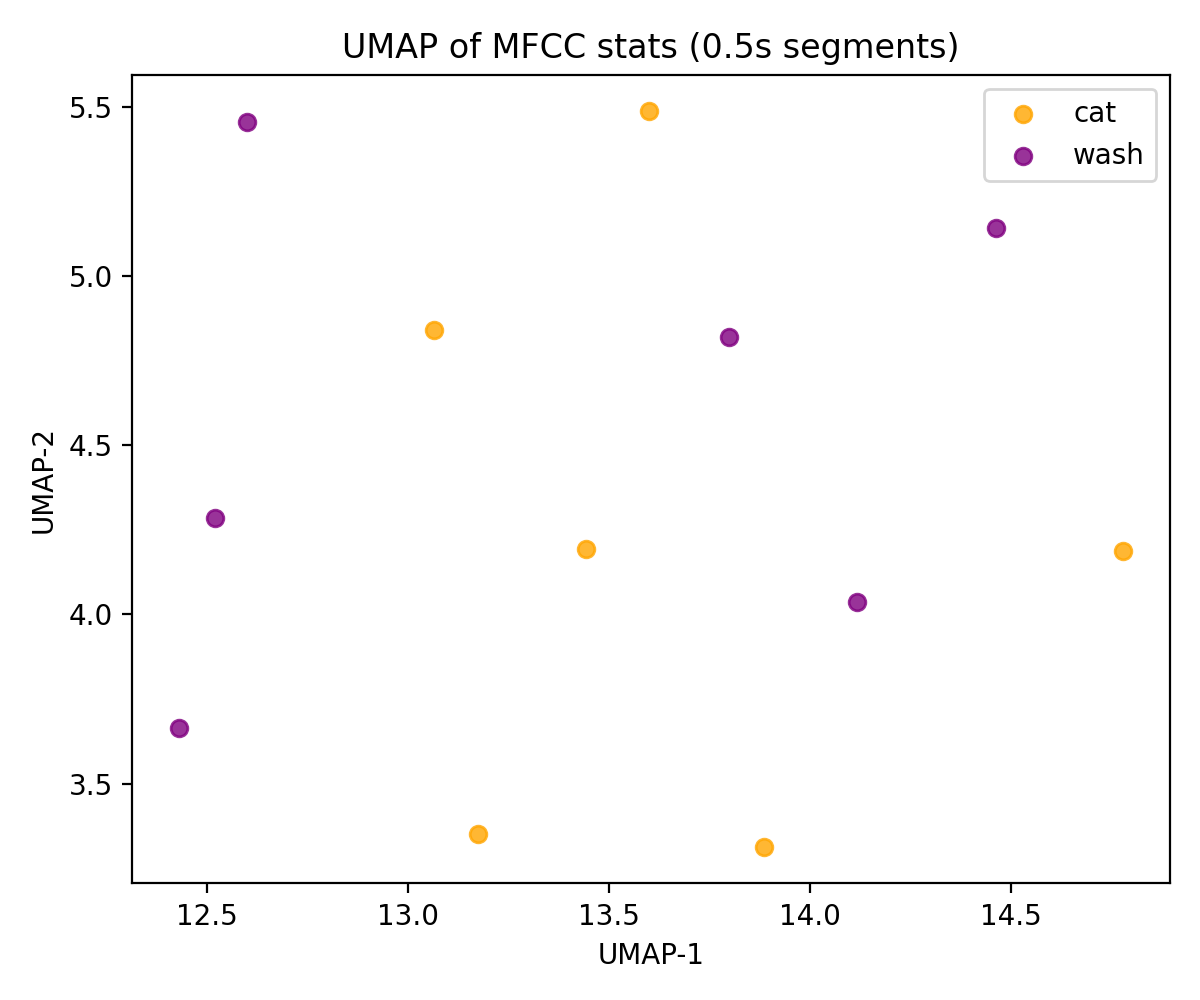
UMAP で 2 次元に圧縮してみる
26 次元ベクトルのままだと人間にはイメージしづらいので、UMAP で 2 次元に圧縮して散布図にしました。
- 入力:各 0.5 秒区間の MFCC 平均+標準偏差(26 次元)
- 出力:UMAP-1(横軸)、UMAP-2(縦軸)の 2 次元座標
- 可視化:ネコ区間をオレンジ、洗濯機区間を紫で描画
UMAP の軸は「周波数」や「時間」そのものではなく、
- 高次元の特徴量空間での違いをうまくばらすために学習された、抽象的な 1 つめの方向(UMAP-1)
- それと独立な 2 つめの方向(UMAP-2)
というイメージです。なので、軸そのものに意味付けをするというより、「点どうしが近いか・離れているか」を見るための座標だと割り切って使いました。
UMAP の結果から分かったこと
UMAP 上にプロットしてみると、ネコ(cat)と洗濯機(wash)の点は、きれいに左右に分裂するわけではなく、ほぼ同じエリアの中に点在 しました。
- もし特徴量が大きく違っていれば、オレンジの塊と紫の塊が、離れた場所に 2 集団として現れます。
- 今回は、両方の点が同じ近辺に散らばっているので、
「MFCC の 26 次元特徴量で見ても、ネコのゴロゴロと洗濯機の連続音は“完全に別物”というより、かなり近い性質の音として扱われている」
と解釈できます。
サンプル数は少ないので厳密な結論ではありませんが、「家電っぽいゴロゴロに聞こえる」という耳の感覚は、シンプルな特徴量空間でもそれなりに筋が通っていた、と言えそうです。
ここ注意(やってみて気になった点)
-
サンプル数が少ない
3 秒×1 本ずつを 0.5 秒に分けただけなので、統計的には心許ないです。本気で分類器を作るなら、もっと多くの録音・条件でデータを集める必要があります。 -
窓長と特徴量設計
0.5 秒の平均+標準偏差は、かなりおおざっぱなまとめ方です。周期性や立ち上がり/終わり方も含めて区別したいなら、もう少し長い時間にする、時間方向のパターンを特徴量に含めるなどの工夫が要りそうです。 -
UMAP の解釈
UMAP の軸そのものには深い意味を持たせていなくて、「似ているサンプル同士が近くに並ぶ座標」くらいの理解で止めています。
まとめ
- ネコのゴロゴロ音と洗濯機の音を、
16kHz モノラル・RMS 正規化・3 秒固定 という最小のルールでそろえてから、スペクトログラムと MFCC+UMAP で可視化してみました。 - スペクトログラムでは、「ネコ=低〜中域の細かいゆらぎ」「洗濯機=特定帯域の持続」という違いがありつつも、エネルギーが乗っている帯域はそこそこ似ていました。
- 0.5 秒ごとに MFCC 13 次元を計算し、その平均+標準偏差の 26 次元ベクトルを UMAP に流すと、ネコ区間と洗濯機区間の点は、だいたい同じところに散らばる結果になりました。
→ 特徴量空間でも「完全に別世界」ではなく、「似たキャラクターの連続音」として扱われている、ということになります。
日常の「なんかこのゴロゴロ、家電っぽいよね」という違和感を、データエンジニア的な前処理と軽い特徴量可視化で確認してみた、という小ネタでした。
次の遊びとしては、この 26 次元特徴量をそのままデータベースに入れてクラスタリングしたり、日によって“いつもと違うゴロゴロ”を検知する異常検知に回してみるのも面白そうです。