ポワソン分布を用いた非負値行列因子分解

非負値行列因子分解 と尤度

非負値行列因子分解（NMF）は、二次元の行列 Y を 2つの正の行列 W と H の積で近似するものです。

この操作をベイズ推定の最大事後確率推定の問題だと見ると、

$$
\mathrm{W}, \mathrm{H} = \text{argmax}_{\mathrm{W}, \mathrm{H}} \left[
\log p(\mathrm{Y} | \mathrm{W H}) + \log p(\mathrm{W}) + \log p(\mathrm{H})
\right]
$$

事前分布 $p(\mathrm{W})$, $p(\mathrm{H})$ は、
負の領域で0、非負の領域で1 をとる一様分布だと考えることができます。

$p(\mathrm{Y} | \mathrm{WH})$ は尤度です。
尤度にガウス分布を用いる場合（ノイズが中心0で分散 $σ$ のガウス分布に従う場合）、
対数尤度は以下のようになります。

$$
\begin{aligned}
\log p(\mathrm{Y} | \mathrm{WH})
&= \sum_{i, j} \log p(y_{i j} \mid f_{i j}) \\
&= \sum_{i, j} \left[-\frac{1}{2 \sigma^2} (y_{i j} - f_{i j})^2
- \frac{1}{2}\log2 - \log \sigma
\right]
\end{aligned}
$$

ここで $f_{i j} = \sum_k w_{i k} h_{k j}$ と置きました。
$\sigma$ の値は W, H の最尤値に影響しません。
そのため、ガウス分布を尤度に用いたときの NMF は、

$$
\mathrm{W}, \mathrm{H} = \text{argmin}_\mathrm{W, H} \sum_{i j} \left[
y_{i j} - \sum_k w_{i k} h_{k j}
\right]^2
\\
\mathrm{s.t.} \;\; w_{i k} \geq 0, \;\; h_{k j} \geq 0
$$

として表すことができます。
これは、以前の投稿で述べた、二乗距離を用いたNMFに一致します。
再帰的な極小値の評価方法は、前回の投稿の通りです。

ポワソン分布

ガウス分布は分散の大きさがスケールに依存しないので、
1と2の差と、100と101の差は同じ程度に大きいと評価することになります。
しかし見方によっては、'2は1の2倍だが、101は100のたかだか1.01倍なので差としては比較的小さい'と考えることもできます。

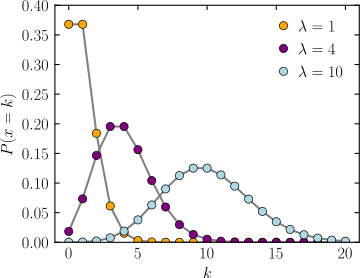
分散がスケールに依存するものとして、ポワソン分布が挙げられます。

引用：wikipedia https://ja.wikipedia.org/wiki/%E3%83%9D%E3%82%A2%E3%82%BD%E3%83%B3%E5%88%86%E5%B8%83

ポワソン分布の分散は、スケール$f$に対して $\sqrt{f}$ に比例します。
大雑把に言うと、1 と 1.1 の差、100 と 101 の差を大体同じ程度に評価します。

ポワソン分布は、ある項目を選んだ人の数とか、ある時間内に計測された光子の数など、
離散的なイベントの数の分布を表す分布としてよく用いられます。

ポワソン分布を用いた時の尤度は、
$$
p(y | f) = \frac{f^y e^{-f}}{y!}
$$
として表されます。

参考文献

細胞の蛍光顕微計測で得られた画像を、ポワソン分布を用いたNMFを使って解析している例を見つけました。

Neher, R. A., Mitkovski, M., Kirchhoff, F., Neher, E., Theis, F. J., & Zeug, A. (n.d.). Blind Source Separation Techniques for the Decomposition of Multiply Labeled Fluorescence Images.
http://doi.org/10.1016/j.bpj.2008.10.068

以下に示す更新式は、上記論文に載っているものですが、更新式自体の導出は記載されていないのでここにまとめたいと思います。

ポワソン分布をNMFに用いる

ポワソン分布をNMFに用いることを考えます。
これまで、「二乗距離」や「一般化KL距離」というように「距離」という言葉を使っていました。
ポワソン分布を尤度に持つときの距離を「ポワソン距離」と呼ぶことにします。

ポワソン距離をNMFに用いるためのコスト関数は、負の対数尤度の $f$ に依存する部分だけを残せばよいので

$$
\mathrm{W}, \mathrm{H} = \text{argmin}_\mathrm{W, H} \sum_{i j} \left[
-y_{i j} \log \sum_k w_{i k} h_{k j} + \sum_k w_{i k} h_{k j}
\right]
\
\mathrm{s.t.} \;\; w_{i k} \geq 0, \;\; h_{k j} \geq 0
\tag{1}
$$

となります。
なお、$Y_{i j}$ がポワソン分布に従って分布する場合、負の値を取ることはありません
（ガウス分布の場合は、負の値になることもあり得ます）。
更新式も $y_{i j}$ が非負であることを用いるので、データに負の値が入っているとうまく行きません。
また、$f_{i j}$ が 0 のときはかならず $y_{i j} = 0$ となるので、
二乗距離を用いた時に比べて、$w_{i k}, h_{k j}$ が零になる場合は少なくなると思われます。

更新式

ポワソン分布を尤度に用いた時も、W, Hそれぞれに対する最適化を繰り返すことで再帰的に最適解（極小解）を求めます。
そのための更新式は以下のとおりです。なお、これらの導出は以下で述べます。

ポワソン距離（欠損値なし）

Yに欠損値が含まれないとすると、更新式は以下のように表すことができます。

$$
w_{i k} \gets w_{i j} \frac{
\sum_j \frac{y_{i j}}{\sum_{k'} w_{i k'} h_{k' j}} h_{k j}
}
{
\sum_j h_{k j}
}
\\
h_{k j} \gets h_{k j} \frac{
\sum_i \frac{y_{i j}}{\sum_{k'} w_{i k'} h_{k' j}} w_{i k}
}
{
\sum_i w_{i k}
}

$$

Python 擬似コードは以下のようになります。

def update_poisson_loss(Y, W, H):
  """  Update W and H with poisson loss  """
  W = W * np.dot(Y / np.dot(W, H), H.T)\
        / np.sum(H, axis=1, keepdims=True)
  H = H * np.dot(W.T, np.dot(W.T, Y) / np.dot(W, H))\
        / np.sum(W, axis=0, keepdims=True)
  return W, H

ポワソン距離（欠損値あり）

前回の投稿 で述べた方法と同様にして、ポワソン距離を用いた時でも欠損値を扱うことができます。

要素が0と1からなるマスク行列 $\mathrm{M}=\{m_{i j}\}$ を用意します。
Yの欠損値に対応する要素には0、それ以外には1 を入れておきます。マスク行列Mを用いると、コスト関数は以下のようになります。

$$
\mathrm{W}, \mathrm{H} = \text{argmin}_\mathrm{W, H} \sum_{i j} \left[
- y_{i j} m_{i j} \log \sum_k w_{i k} h_{k j} + \sum_k w_{i k} h_{k j} m_{i j}
\right]
\\
\mathrm{s.t.} \;\; w_{i k} \geq 0, \;\; h_{k j} \geq 0
\tag{2}
$$

Yにnanなどが入っている場合、Yとの演算がうまくできなかったりするので、暫定的に0などを代入しておく必要が有ります。

この場合の更新式は、以下のようになります。

$$
w_{i k} \gets w_{i j} \frac{
\sum_j \frac{y_{i j} m_{i j}}{\sum_{k'} w_{i k'} h_{k' j}} h_{k j}
}
{
\sum_j h_{k j} m_{i j}
}
\\
h_{k j} \gets h_{k j} \frac{
\sum_i \frac{y_{i j} m_{i j}}{\sum_{k'} w_{i k'} h_{k' j}} w_{i k}
}
{
\sum_i w_{i k} m_{i j}
}

$$

Python 擬似コードは次の通りです。

def update_poisson_loss_w_mask(Y, W, H, M):
  """  Update W and H with poisson loss with mask """
  W = W * np.dot(Y * M / np.dot(W, H), H.T)\
        / np.dot(M, H.T)
  H = H * np.dot(W.T, np.dot(W.T, Y) * M / np.dot(W, H))\
        / np.dot(W.T, M)
  return W, H

更新式の導出

更新式を導出するための戦略は、前回の記事と同様です。
W、Hを順番に最適化していきます。
まず式(1)（欠損値ありの場合は式(2)）で表されるをWの関数と見て最適化します。ただし、このコスト関数は少し複雑な形状をしているので、うまく上から抑える関数を探します。

ポワソン距離（欠損値なし）

$-\log x$は下に凸の関数であることから、Jensenの不等式を適用すると
$$
\begin{aligned}
-\log \sum_k w_{i k} h_{k j}
&= -\log \sum_k r_{i j k} \frac{w_{i k} h_{k j}}{r_{i j k}} \\
& \leq \sum_k r_{i j k} \log \frac{w_{i k} h_{k j}}{r_{i j k}}
\end{aligned}
\tag{3}
$$
が成り立ちます。ここで、$r_{i j k}$ は $\sum_k r_{i j k} = 1$ を満たす正の定数です。

なお、等号が成立する条件は、前記事の二乗距離の時と同様です。
$$
r_{i j k} = \frac{w_{i k} h_{k j}}{\sum_{k'} w_{i k'} h_{k' j}}
$$

式(3)を式(1)に代入して求まる補助関数

$$
\begin{aligned}
\mathrm{G(W; W')} &=
\sum_{i j}\left[
-y_{i j} \sum_k r_{i j k} \log \frac{w_{i k} h_{k j}}{r_{i j k}}
+ \sum_k w_{i k} h_{k j}
\right]
\end{aligned}
$$

をWについて最適化します。勾配が0になる点を探すと

$$
\begin{aligned}
\frac{\partial \mathrm{G(W; W')}}{w_{i k}} =
\sum_j \left[
-\frac{y_{i j} r_{i j k}}{w_{i k}} + h_{k j}
\right] = 0
\;\;\to\;\;
w_{i k} &= \frac{\sum_j y_{i j} r_{i j k}}{\sum_j h_{k j}}
= w'_{i k} \frac{
\sum_j \frac{y_{i j}}{\sum_{k'} w_{i k'} h_{k' j}} h_{k j}
}
{
\sum_j h_{k j}
}
\end{aligned}
$$

となり、G(W; W') の最小値はコスト関数を必ず小さくすることから、有効な更新式になっています。

ポワソン距離（欠損値あり）

欠損値があるときも、前節の式(3)を式(2)に代入して、同様の議論を行います。
補助関数は

$$
\begin{aligned}
\mathrm{G(W; W')} &=
\sum_{i j}\left[
-y_{i j} m_{i j k} \sum_k r_{i j k} \log \frac{w_{i k} h_{k j}}{r_{i j k}}
+ \sum_k w_{i k} h_{k j} m_{i j}
\right]
\end{aligned}
$$

となるので、勾配が0になるWの値を求めると、

$$
\begin{aligned}
\frac{\partial \mathrm{G(W; W')}}{w_{i k}} =
\sum_j \left[
-\frac{y_{i j} m_{i j} r_{i j k}}{w_{i k}} + h_{k j} m_{i j}
\right] = 0
\;\;\to\;\;
w_{i k} &= \frac{\sum_j y_{i j} m_{i j} r_{i j k}}{\sum_j h_{k j} m_{i j}}
= w'_{i k} \frac{
\sum_j \frac{y_{i j} m_{i j}}{\sum_{k'} w_{i k'} h_{k' j}} h_{k j}
}
{
\sum_j h_{k j} m_{i j}
}
\end{aligned}
$$

が示せます。

まとめ

最初にも述べましたが、ポワソン分布を用いることで、Y と WH の差として許される大きさが、WHの値自体に依存するようになります。
これがガウス分布と大きく異なる点です。

非負の値を扱うときは、何かカウントデータを扱うという時が多いように思います。
二乗距離でうまく行かないときは、ポワソン距離も考えてみてはどうでしょうか。