おさらい
前回は求めたいパラメータの式が一次式 $y = ax + b$ の場合の実装をしました。今回は二次式だったら…というのを見ていきましょう。といっても必要な計算式はすでにわかっているので、これが実装できればいいですね。
求めたい式
今回求めたい式は $y = ax^2 + b$ と設定します。求めるパラメータが $a$, $b$ の2つということは変わりません。
シートの準備
シートの準備をします。シートは前回のシートをそのまま利用しましょう。
データや計算式、グラフの設定を若干変更します。
データ
今回のデータはこのようにしました。
| No | x | y |
|---|---|---|
| 1 | -1.55 | 1.55 |
| 2 | -1.13 | 1.27 |
| 3 | -0.94 | 1.17 |
| 4 | -0.34 | 0.98 |
| 5 | -0.28 | 0.97 |
| 6 | 0.1 | 0.95 |
| 7 | 0.41 | 0.99 |
| 8 | 0.79 | 1.11 |
| 9 | 1.27 | 1.36 |
| 10 | 1.67 | 1.65 |
A1:C11の範囲に上記データを入力してください。
グラフまわりの準備
推測値(推測グラフ)用のデータ(H列)は -2.0 から -0.2 刻みで 2.0 まで準備すればいいでしょう。
また、I2セルの計算式は $ax^2 + b$ にあわせて以下のように変更し、オートフィルで計算式をコピーします。
$\qquad$ =$F$1*(H2^2)+$F$2
横軸、縦軸の範囲についても変更します。以下に変更箇所をまとめておきます。
| 変更箇所 | 変更内容 |
|---|---|
| データ | 上記表の内容 |
| H列 | -2.0 から 0.2 刻みで 2.0 まで |
| I2セル | =$F$1*(H2^2)+$F$2 |
| I列 | I2セルの計算式をコピー |
| 軸の設定値 | 最小値 | 最大値 |
|---|---|---|
| 横軸 | -2.2 | 2.2 |
| 縦軸 | 0.8 | 2.2 |
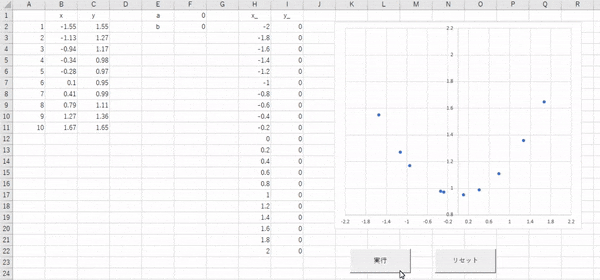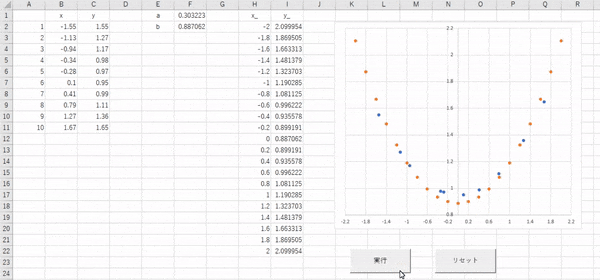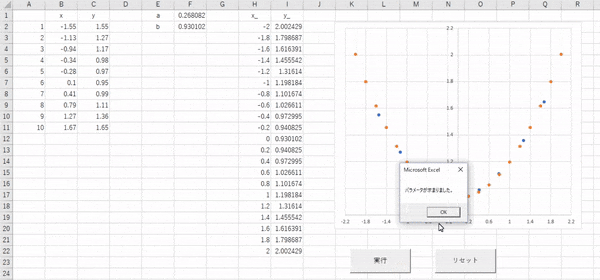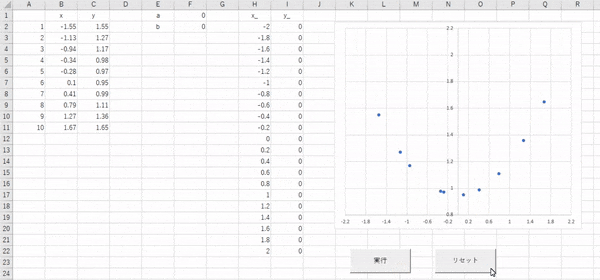
シート完成
このような感じになっていればOKです。

コードの変更
前回のコードを若干変更します。
myFunction() の変更
式の実装部分を今回の式に合わせて変更します。
Private Function myFunction(ByRef a As Double, ByRef x As Double, ByRef b As Double) As Double
'y = ax^2 + b
myFunction = a * x ^ 2 + b
End Function
まぁ、見たままですね。
メイン部分の変更
「Click_実行」プロシージャを少し変更します。
定数の設定
定数を以下の値に設定します。(前回と同じ値のものもあります。)
| 定数 | 値 | 意味 |
|---|---|---|
| LR | 0.001 | 学習率 |
| ERR_POINT | 0.001 | 学習終了判定誤差 |
| MAX_LOOP_COUNT | 2000 | 最大ループカウント数 |
勾配を求める式を変更
勾配を求める式は
$\qquad$ (推測値 - 正解値) * そのパラメータにかかる入力値
で表されていました。
今回、パラメータ $a$ にかかる入力値は $x^2$なので、そのように変更します。パラメータ $b$ に関しては入力値は 1 なのでそのままです。
'[10]a, b の勾配を求める(sum((推測値 - 正解値) * そのパラメータにかかる入力値 の式))
y = .Cells(r, 3).Value
grad_a = grad_a + ((y_ - y) * (x ^ 2)) 'この式を変更
grad_b = grad_b + ((y_ - y) * 1)
ステータスバーの表示桁数を変更
誤差を小数第三位まで表示するようにします。
'[12]回数をカウントアップして、回数、誤差をステータスバーに表示
cnt = cnt + 1
Application.StatusBar = cnt & "回 / E = " & WorksheetFunction.Round(E, 3)
実行してみよう!
では【実行】ボタンを押して実行してみましょう。
このような感じになると思います。
オレンジの点(推測値)が徐々に青い点(正解値)に重なるように動いていっているのがわかりますね。
まとめ
ほんのわずかの変更で二次式にも対応できました。
今回も入力 1 出力 1 のデータでしたが、入力が複数ある場合も少しの変更で対応することができます。
さまざまな関数が同じアルゴリズムで対応できるというのが興味深いですね。
また、パラメータの調整に関していえば、推測(した出力)値さえわかっていればよく、それがどのような関数によって出力されたかということは気にしていないというのも汎用性の高さがうかがえますね。
今回のコード
一応全コードを載せておきます。
Option Explicit
Public Sub Click_リセット()
With wsData2D
.Range("F1").Value = 0
.Range("F2").Value = 0
End With
End Sub
Private Function myFunction(ByRef a As Double, ByRef x As Double, ByRef b As Double) As Double
'y = ax^2 + b
myFunction = a * x ^ 2 + b
End Function
'[1]メインの処理
Public Sub Click_実行()
Dim a As Double 'パラメータ a(傾き)
Dim b As Double 'パラメータ b(切片)
Dim grad_a As Double 'パラメータ a に関する誤差関数の勾配
Dim grad_b As Double 'パラメータ b に関する誤差関数の勾配
Dim E As Double '誤差
Dim x As Double '入力値
Dim y As Double '(正しい)出力値、正解ラベル
Dim y_ As Double '推測値
Dim r As Long '行カウンタ
Dim cnt As Long '回数カウンタ
Const LR As Double = 0.001 '学習率
'--
Const ERR_POINT As Double = 0.001 '学習終了判定誤差(0.1 は恣意的に決めた値)
'--
Const MAX_LOOP_COUNT As Long = 2000 '最大ループカウント数
'[2]パラメータ a, b の初期値にランダムな値を設定する
Randomize
a = Rnd
b = Rnd
With wsData2D
'[3]パラメータを更新していい感じの値にするために処理を繰り返す
cnt = 0
Do
'------------------------------------------------
'[4]いまのパラメータでの誤差を求める(E:誤差)
E = 0
For r = 2 To 10
'[5]いまのパラメータでの推測値を求める
x = .Cells(r, 2).Value
y_ = myFunction(a, x, b)
'[6-1]誤差関数
y = .Cells(r, 3).Value
E = E + ((y - y_) ^ 2)
Next
'[6-2]誤差関数
E = E * 0.5
'------------------------------------------------
'[7]誤差が 学習終了判定誤差 未満ならループを抜ける
If E < ERR_POINT Then
Exit Do
End If
'------------------------------------------------
'[8]勾配を求めてパラメータ a, b を更新する
grad_b = 0
grad_a = 0
For r = 2 To 10
'[9]いまのパラメータでの推測値を求める([4]と同じ)
x = .Cells(r, 2).Value
y_ = myFunction(a, x, b)
'[10]a, b の勾配を求める(sum((推測値 - 正解値) * そのパラメータにかかる入力値 の式))
y = .Cells(r, 3).Value
' grad_a = grad_a + ((y_ - y) * x)
' grad_b = grad_b + ((y_ - y) * 1)
'--
grad_a = grad_a + ((y_ - y) * (x ^ 2)) 'この式を変更
'--
grad_b = grad_b + ((y_ - y) * 1)
Next
'[11]勾配に学習率を掛けてパラメータ a, b を更新する
a = a - (LR * grad_a)
b = b - (LR * grad_b)
'------------------------------------------------
'[12]回数をカウントアップして、回数、誤差をステータスバーに表示
cnt = cnt + 1
'--
Application.StatusBar = cnt & "回 / E = " & WorksheetFunction.Round(E, 3)
'--
'[13]10回に1回グラフを更新
If cnt Mod 10 = 0 Then
DoEvents
DoEvents
.Range("F1").Value = a
.Range("F2").Value = b
End If
'[14]無限ループ回避のため、cnt > MAX_LOOP_COUNT で強制的にループを抜ける
Loop Until cnt >= MAX_LOOP_COUNT
'[15]求まったパラメータ a, b の値をセルに格納
.Range("F1").Value = a
.Range("F2").Value = b
End With
MsgBox "パラメータが求まりました。"
Application.StatusBar = False
End Sub
--Excel VBA でニューラルネットワークをフルスクラッチしてみる--
Excel VBAでニューラルネットワークをフルスクラッチしてみる的な記事は以下のブログに移動しました。
無限不可能性ドライブ