AICとBICの導出を理解したい(後編)

はじめに

• 渡辺澄夫 データ解析(2017) 「(13)モデルの評価」「(14)モデルの評価」の読解メモ。
• AICとBICの導出について理解できる範囲でまとめた。

BICの導出

• 学習損失を$\hat{w}$でテーラー展開して2次の項までで近似する。
• 多次元のテーラー展開

\begin{align}
f(x)&=f(a)+\sum_i\nabla_i(a) (x-a)_i+\frac{1}{2!}\sum_{ij}\nabla_{ij}^2(a) (x-a)_i(x-a)_j+\cdots\\
&\nabla_i=\frac{\partial f}{\partial x_i},\quad \nabla_{ij}^2=\frac{\partial^2 f}{\partial x_i\partial x_j}\\
T(w)&=-\frac{1}{n}\sum_{i=1}^n \log p(x_i|w)\quad 学習損失\\
T(w)&\simeq T(\hat{w})+\frac{1}{2}(w-\hat{w})^t\nabla^2T(\hat{w})(w-\hat{w})+\cdots\quad (\hat{w}は最尤推定量で\nabla T(\hat{w})=0)
\end{align}

• 自由エネルギーFをラプラス近似する。
• $n$が大きくなると指数関数の効果により$\hat{w}$の近傍が優勢となる。

\begin{align}
F&=-\log\int\phi(w)\prod_{i=1}^np(x_i|w)dw\quad 自由エネルギー\\
&=-\log\int\phi(w)\exp(-nT(w))dw\\
&=-\log\int\phi(w)\exp\left(
-nT(\hat{w})-\frac{n}{2}(w-\hat{w})^t\nabla^2T(\hat{w})(w-\hat{w})+\cdots
\right)dw\\
&\simeq -\log \phi(\hat{w})+nT(\hat{w})-\frac{d}{2}\log(2\pi)+\frac{d}{2}\log(n)+\frac{1}{2}\log|\nabla^2T(\hat{w})|
\end{align}

• ここで以下の関係式を使用した。

\begin{align}
\int\exp\left(-\frac{1}{2}x^t\Sigma^{-1}x\right)dx=(2\pi)^{\frac{d}{2}}|\Sigma|^{\frac{1}{2}},\quad \Sigma^{-1}=n\nabla^2T(\hat{w})
\end{align}

• $\phi(w)=1$として自由エネルギーFをラプラス近似した場合の主要項がBICに相当する。

\begin{align}
\mathrm{BIC}&=2nT(\hat{w})+d\log(n)
\end{align}

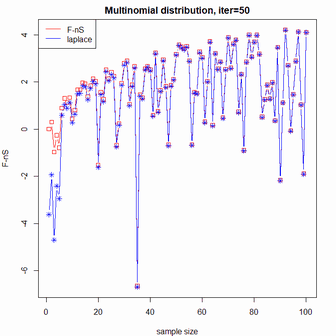
自由エネルギーFとラプラス近似の比較

多項分布

• 各目$k$の発生確率が$w_k(k=1,\cdots K)$であるサイコロを考える。
• 出た目を表す変数を$x_k$(0または1)とする。$\sum_{k=1}^K x_k=1$
• $n$回振って$k$の目が出た回数を$n_k$とする。$C$はディリクレ分布の正規化定数。

\begin{align}
p(x|w)&=\prod_{k=1}^Kw_k^{x_k}\quad 確率分布\\
S&=-\int p(x|w)\log p(x|w)dx=-\sum_{k=1}^K w_k\log w_k\quad エントロピー\\
\phi(w)&=C(a_0)\prod_{k=1}^Kw_k^{a_0-1}\quad 事前分布(ディリクレ分布)\\
\phi(w)p(X|w)&=C(a_0)\prod_{k=1}^Kw_k^{n_k+a_0-1}\quad 事後分布\\
F&=-\log\int\phi(w)p(X|w)dw\quad 自由エネルギー\\
&=-\log\frac{C(a_0)}{C(n_k+a_0)}=\log C(n_k+a_0)-\log C(a_0)\\
C(\alpha)&=\frac{\Gamma\left(\sum_{k=1}^K \alpha_k\right)}
{\prod_{k=1}^K\Gamma(\alpha_k)}
\end{align}

• 自由エネルギーFのラプラス近似$(d=K-1)$

\begin{align}
F&\simeq -\log \phi(\hat{w})+nT(\hat{w})-\frac{d}{2}\log(2\pi)+\frac{d}{2}\log(n)+\frac{1}{2}\log|\nabla^2T(\hat{w})|\\
\phi(\hat{w})&=C(a_0)\prod_{k=1}^K\hat{w}_k^{a_0-1}\\
T(w)&=-\frac{1}{n}\sum_{i=1}^n\log p(x_i|w)=-\frac{1}{n}\sum_{i=1}^n\log\prod_{k=1}^K w_k^{x_{ik}}
=-\sum_{k=1}^K\frac{n_k}{n}\log w_k\\
T(w)&=-\sum_{k=1}^K \hat{w}_k\log w_k,\quad
T(\hat{w})=-\sum_{k=1}^K \hat{w}_k\log\hat{w}_k,\quad
\hat{w}_k=\frac{n_k}{n}\quad 最尤推定量\\
\nabla_i T(w)&=-\frac{\hat{w}_i}{w_i}+\frac{\hat{w}_K}{w_K}\quad(i=1,\cdots K-1)\\
\nabla^2_{ii} T(w)&=\frac{\hat{w}_i}{w_i^2}+\frac{\hat{w}_K}{w_K^2},\quad
\nabla^2_{ij} T(w)=\frac{\hat{w}_K}{w_K^2}\quad(i\ne j)\\
\nabla^2_{ii} T(\hat{w})&=\hat{w}_i^{-1}+\hat{w}_K^{-1},\quad
\nabla^2_{ij} T(\hat{w})=\hat{w}_K^{-1}\quad(i\ne j),\quad
|\nabla^2T(\hat{w})|=\prod_{k=1}^K \hat{w}_k^{-1}
\end{align}

# 自由エネルギーの真値とラプラス近似の比較
# 多項分布

# Normalizing constant of Dirichlet distribution
my_log_C = function(a){
  lgamma(sum(a))-sum(lgamma(a))
}

a0 = 1 # hyperparameter
w0 = c(0.3,0.3,0.4); w0=w0/sum(w0)
K = length(w0)
d = K - 1
N = 100

S0 = -sum(w0*log(w0))

set.seed(3)
par(mfrow=c(1,1))
par(mar=c(4,4,2,2))
for(iter in 1:50){
  F_true = numeric()
  F_laplace = numeric()
  for(n in 1:N){
    nk = as.vector(rmultinom(n=1,size=n,prob=w0))
    F_true[n] = my_log_C(nk+a0)-my_log_C(rep(a0,K)) - n*S0
    w = nk/n
    log_phi0 = my_log_C(rep(a0,K)) + (a0-1)*sum(ifelse(w==0,0,log(w)))
    Tw = -sum(ifelse(w==0,0,w*log(w)))
    detH = 1/prod(ifelse(w==0,1,w))
    f = -log_phi0+n*Tw-d/2*log(2*pi)+d/2*log(n)+1/2*log(detH) - n*S0
    F_laplace[n] = ifelse(is.infinite(f),NA,f)
  }
  msg = sprintf("Multinomial distribution, iter=%d",iter)
  ymin = min(F_true,F_laplace,na.rm=T)
  ymax = max(F_true,F_laplace,na.rm=T)
  plot(x=F_true,type="b",col="red",ylim=c(ymin,ymax),xlab="sample size",ylab="F-nS",main=msg,pch=0)
  lines(x=F_laplace,type="b",col="blue",pch=8)
  legend("topleft",legend=c("F-nS","laplace"),lty=1,col=c("red","blue"))
  dev.flush()
  Sys.sleep(0.2)
}

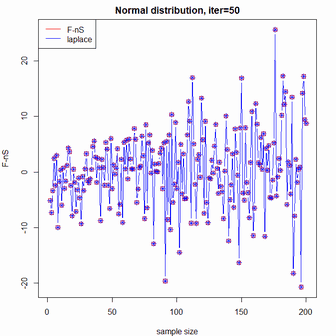
正規分布

• 一次元の正規分布$p(x|a,s)$を対象とする。$a=\mu,s=\sigma^{-2}$
• 事前分布は正規逆ガンマ分布$\phi(a,s)$とする。$r,h$はハイパーパラメータ。
• $Z$は正規逆ガンマ分布の正規化定数。

\begin{align}
Z(r,A,C)&=\iint s^r\exp\left(
-\frac{sA}{2}(a-B)^2-\frac{C}{2}s\right)dads\\
&=\sqrt{\frac{2\pi}{A}}\left(\frac{2}{C}\right)^\alpha\Gamma(\alpha),\quad
\alpha=r+\frac{1}{2}\\
p(x|a,s)&=(2\pi)^{-\frac{1}{2}}s^{\frac{1}{2}}\exp\left(-\frac{s}{2}(x-a)^2\right)\quad 確率分布\\
S&=-\int p(x|a,s)\log p(x|a,s)dx=\frac{1}{2}(1+\log(2\pi)-\log s)\quad エントロピー\\
\phi(a,s)&= Z(r,h,h)^{-1}s^r\exp\left(-\frac{hs}{2}(a^2+1)\right)\quad 事前分布(正規逆ガンマ)\\
\phi(a,s)p(X|a,s)&=Z(r,h,h)^{-1}(2\pi)^{-\frac{n}{2}}s^{r+\frac{n}{2}}\exp\left(
-\frac{sA}{2}(a-B)^2-\frac{C}{2}s\right)\quad 事後分布\\
&A=n+h,B=\frac{\sum x_i}{A},C=\sum x_i^2+h-AB^2\\
F&=-\log\int\phi(a,s)p(X|a,s)dads\quad 自由エネルギー\\
&=\frac{n}{2}\log(2\pi)+\log Z(r,h,h)-\log Z\left(r+\frac{n}{2},A,C\right)
\end{align}

• 自由エネルギーFのラプラス近似$(d=2)$

\begin{align}
F&\simeq -\log\phi(\hat{w})+nT(\hat{w})-\frac{d}{2}\log(2\pi)+\frac{d}{2}\log(n)+\frac{1}{2}\log|\nabla^2T(\hat{w})|\\
T(w)&=-\frac{1}{n}\sum_{i=1}^n\log p(x_i|a,s)\\
&=-\frac{1}{2}\log s+\frac{1}{2}\log(2\pi)+\frac{s}{2n}\sum_{i=1}^n(x_i-a)^2\\
\nabla_aT(w)&=-\frac{s}{n}\sum_{i=1}^n(x_i-a)=0\\
\nabla_sT(w)&=-\frac{1}{2s}+\frac{1}{2n}\sum_{i=1}^n(x_i-a)^2=0\\
\hat{a}&=\frac{1}{n}\sum_{i=1}^n x_i,\quad
\hat{s}=\frac{n}{\sum_{i=1}^n (x_i-\hat{a})^2}\quad 最尤推定量\\
T(\hat{w})&=-\frac{1}{2}\log \hat{s}+\frac{1}{2}\log(2\pi)+\frac{1}{2}\\
\nabla^2_{aa}T(w)&=s,\quad
\nabla^2_{as}T(w)=a-\hat{a},\quad
\nabla^2_{ss}T(w)=\frac{1}{2s^2}\\
\nabla^2_{aa}T(\hat{w})&=\hat{s},\quad
\nabla^2_{as}T(\hat{w})=0,\quad
\nabla^2_{ss}T(\hat{w})=\frac{1}{2\hat{s}^2},\quad
|\nabla^2T(\hat{w})|=\frac{1}{2\hat{s}}
\end{align}

# 自由エネルギーの真値とラプラス近似の比較
# 正規分布

r = 0 # hyperparameter
h = 0 # hyperparameter

my_log_Z = function(r,A,C){
  if(A==0) return(0)
  alpha = r+1/2
  0.5*log(2*pi/A)+alpha*log(2/C)+lgamma(alpha)
}
my_log_phi = function(a,s){
  if(h==0) return(0)
  -my_log_Z(r,h,h)+r*log(s)-h*s/2*(a^2+1)
}

a0 = 0 # mean
s0 = 1 # 1/sigma^2
d = 2
N = 200

S0 = (1+log(2*pi)-log(s0))/2

set.seed(3)
par(mfrow=c(1,1))
par(mar=c(4,4,2,2))
for(iter in 1:50){
  F_true = numeric()
  F_laplace = numeric()
  for(n in 1:N){
    xn = rnorm(n,mean=a0,sd=1/sqrt(s0))
    A = n+h
    B = sum(xn)/A
    C = sum(xn^2)+h-A*B^2
    f = (n/2*log(2*pi)+my_log_Z(r,h,h)-my_log_Z(r+n/2,A,C)) - n*S0
    F_true[n] = ifelse(is.infinite(f),NA,f)
    am = mean(xn)
    sm = 1/mean((xn-am)^2)
    Tw = -0.5*log(sm)+0.5*log(2*pi)+0.5
    f = -my_log_phi(am,sm)+n*Tw-d/2*log(2*pi)+d/2*log(n)-0.5*log(2*sm) - n*S0
    F_laplace[n] = ifelse(is.infinite(f),NA,f)
  }
  msg = sprintf("Normal distribution, iter=%d",iter)
  ymin = min(F_true,F_laplace,na.rm=T)
  ymax = max(F_true,F_laplace,na.rm=T)
  plot(x=F_true,type="b",col="red",ylim=c(ymin,ymax),xlab="sample size",ylab="F-nS",main=msg,pch=0)
  lines(x=F_laplace,type="b",col="blue",pch=8)
  legend("topleft",legend=c("F-nS","laplace"),lty=1,col=c("red","blue"))
  dev.flush()
  Sys.sleep(0.2)
}

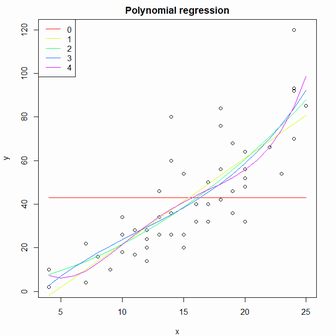
予測モデルの評価

• サンプルデータcarsについて多項式回帰分析を実施。
• AICでは二次式、BICでは一次式が最適なモデルとなる。

df = cars
colnames(df) = c("x","y")

N = nrow(df)
par(mfrow=c(1,1))
par(mar=c(4,4,2,2))
plot(x=df$x,y=df$y,type="p",xlab="x",ylab="y",main="Polynomial regression")
cols = rainbow(5)
aic = numeric()
bic = numeric()
aic_v = numeric()
bic_v = numeric()
for(deg in 0:4){
  if(deg == 0){
    lm.fit = lm(y~1,data=df)
  }else{
    lm.fit = lm(y~poly(x,deg),data=df)
  }
  xp = seq(from=min(df$x),to=max(df$x),by=1)
  lines(x=xp,y=predict(lm.fit,newdata=data.frame(x=xp)),type="l",col=cols[deg+1])
  s2 = sum(lm.fit$residuals^2)
  log_L = N/2*log(2*pi*s2/N)+N/2 # -sum log p(y_i|x_i,w) at MLE
  aic_v[deg+1] = 2*log_L + 2*(deg+2)
  bic_v[deg+1] = 2*log_L + log(N)*(deg+2)
  aic[deg+1] = AIC(lm.fit)
  bic[deg+1] = BIC(lm.fit)
}
legend("topleft",legend=0:4,lty=1,col=cols)
data.frame(deg=0:4,aic,aic_v,bic,bic_v)

> data.frame(deg=0:4,aic,aic_v,bic,bic_v)
  deg      aic    aic_v      bic    bic_v
1   0 469.8024 469.8024 473.6265 473.6265
2   1 419.1569 419.1569 424.8929 424.8929
3   2 418.7721 418.7721 426.4202 426.4202
4   3 419.8850 419.8850 429.4451 429.4451
5   4 420.2771 420.2771 431.7492 431.7492