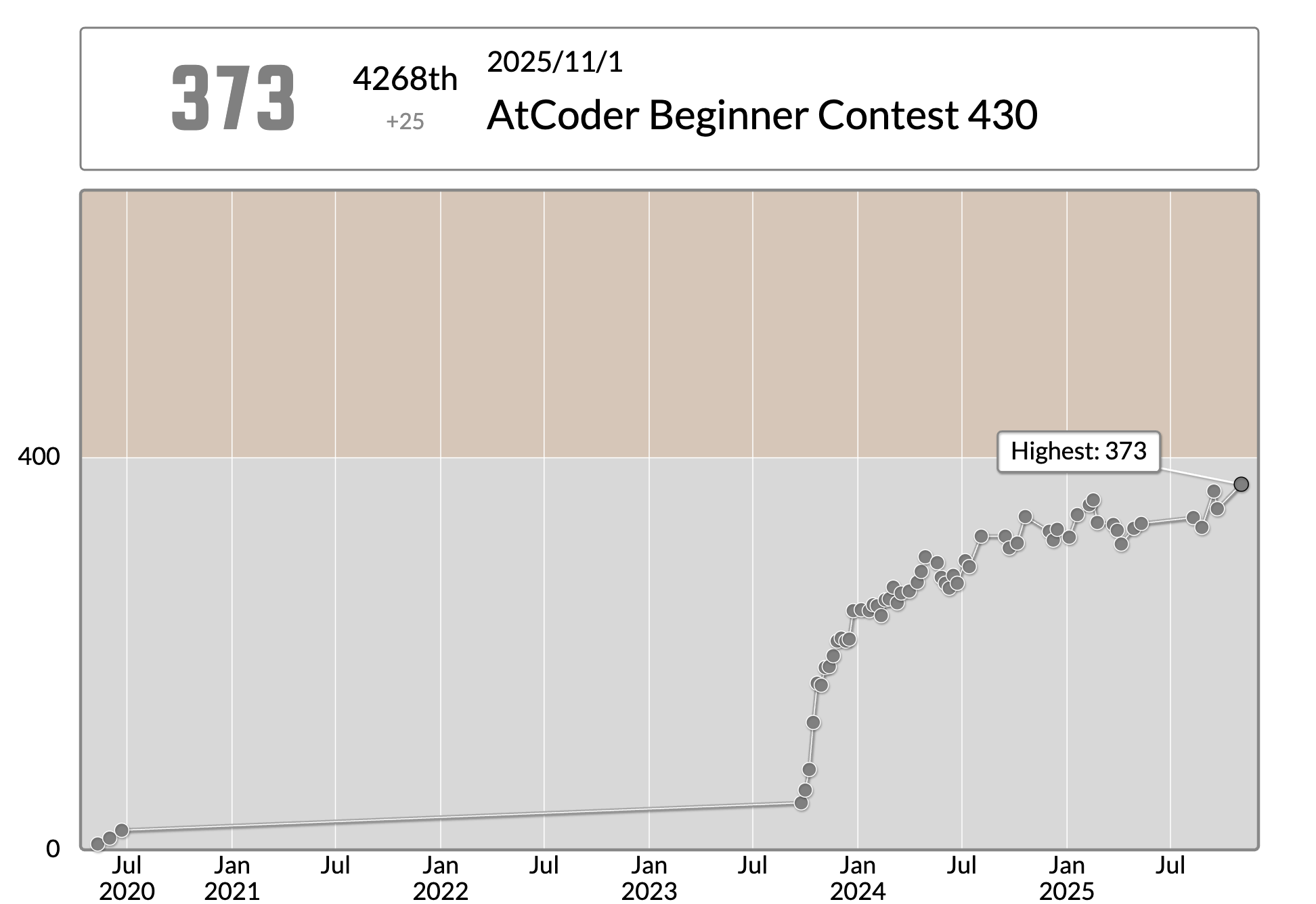
久しぶりのAtCoder参加です
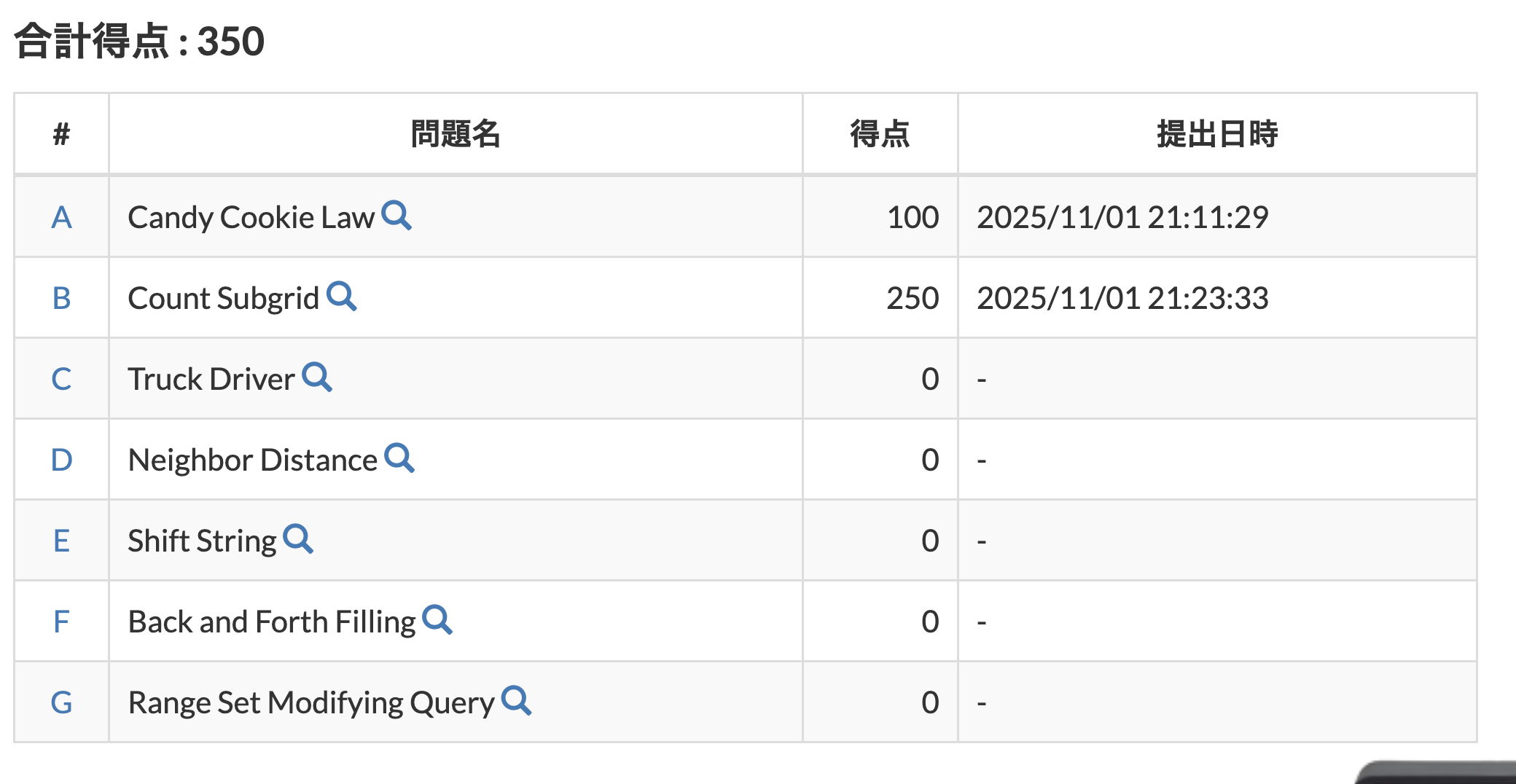
結果
今回はABの2完でした。
ふりかえり
A問題
- 問題
- 回答
高橋君の住む AtCoder 国には「飴を
A 個以上所持している人はクッキーを
B 個以上所持していなければならない」という奇妙な法律があります。
から、飴の所持数がaより少ない もしくは クッキーの所持数をb個以上となっている場合は法律違反していない場合は法律違反していないことがわかります。
ただし、
高橋君がこの法律に違反しているかどうか判定してください。
とあることから、法律違反している場合を求める必要があります。この場合は条件が反転するのでnotが必要です。(これに気づかず少しハマりました。)
main :: IO ()
main = do
[a, b, c, d] <- getInts
printYn $ not $ a > c || b <= d
B問題
- 問題
- 回答
グリッドの問題なので少し焦りますが、1≤M≤N≤10であることから全探索で十分解けることがわかります。
main :: IO ()
main = do
[n, m] <- getInts
ss <- replicateM n getLine
let g = buildGrid ((1, 1), (n, n)) ss
ans =
length $
nubOrd
[ [ g ! (ii, jj) | ii <- [i .. i + m - 1], jj <- [j .. j + m - 1]
]
| i <- [1 .. n - m + 1],
j <- [1 .. n - m + 1]
]
print ans
C問題(upsolved)
- 問題
- 回答
aとbの個数を累積和で保持しておき、
Sのl文字目からr文字目までに含まれるaの個数がA以上
から
Sのl文字目からr文字目までに含まれるbの個数がB未満
までの組の個数を計算します。
最初は累積和を作ってlとrの組を全探索で計算したのですが、その場合は
- 計算量が
O(N^2) 1≤N≤3×10^5
の制約より、最大で計算量が9×10^10程度になることからTLEになります。
その時の回答は以下の通りです。
main :: IO ()
main = do
[n, a, b] <- getInts
s <- getLine
let m =
M.fromAscList $
scanl'
( \(idx, (acnt, bcnt)) c ->
if c == 'a'
then (idx + 1, (acnt + 1, bcnt))
else (idx + 1, (acnt, bcnt + 1))
)
(0, (0, 0))
s
ans =
[ (l + 1, r)
| l <- [0 .. n - 1],
let (la, lb) = fromJust $ M.lookup l m,
r <- [l + 1 .. n],
let (ra, rb) = fromJust $ M.lookup r m,
ra - la >= a,
rb - lb < b
]
print $ length ans
ではどうすれば良いのかと言うと、累積和を作った後に二分探索を使うことになります。lを決めてrを二分探索で求めればよいです。この場合計算量はO(NlogN)になります。
main :: IO ()
main = do
[n, a, b] <- getInts
s <- getLine
let sa = VU.fromList $ scanl' (\acc c -> bool acc (acc + 1) (c == 'a')) (0 :: Int) s
sb = VU.fromList $ scanl' (\acc c -> bool acc (acc + 1) (c == 'b')) (0 :: Int) s
ans =
sum
[ rMax - rMin + 1
| l <- [1 .. n],
let cla = sa VU.! (l - 1)
clb = sb VU.! (l - 1)
rMin = fromMaybe (n + 1) (lookupGEIdx (cla + a) sa)
rMax = maybe n pred (lookupGEIdx (clb + b) sb),
rMax >= rMin
]
print ans
全体を振り返って
Cは二分探索を使えばいけそう、というところまで気づいたのですがそこからどうすれば良いかわからずタイムアップしてしまいました。
累積和 + 二分探索のパターンもしっかりマスターしたいです。