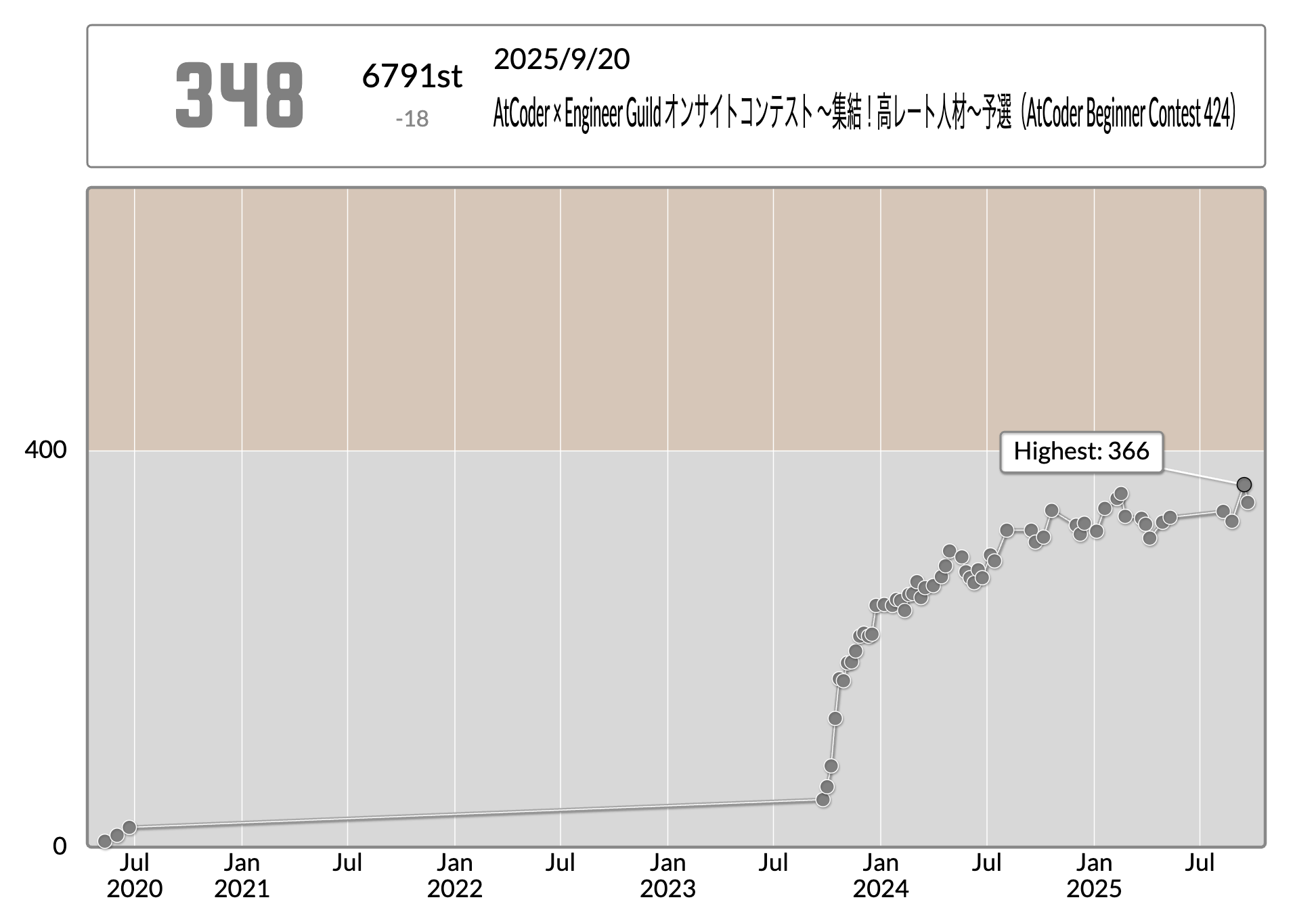
AtCoder Rated参加です
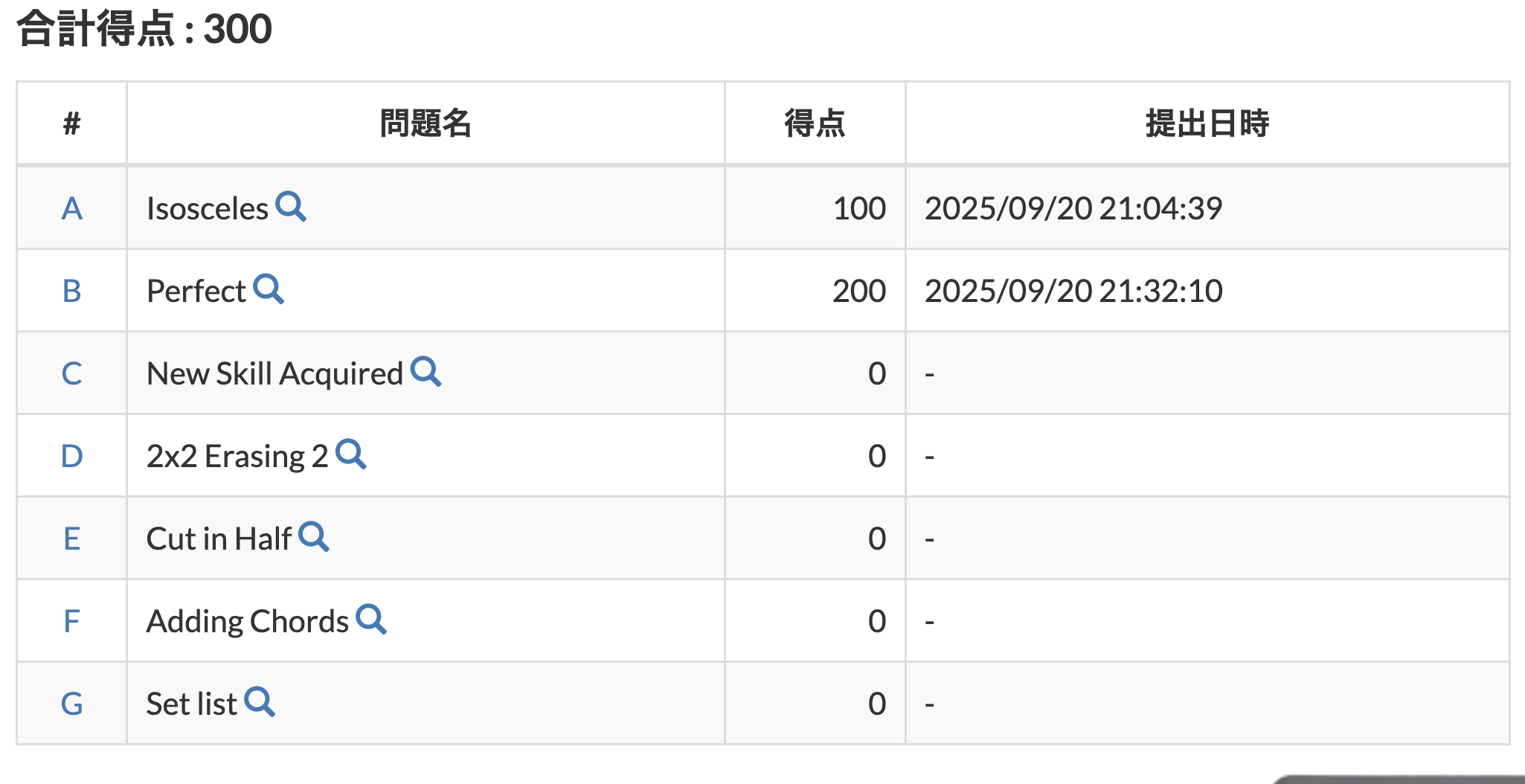
結果
今回はABの2完でした。
ふりかえり
A問題
- 問題
- 回答
二等辺三角形なので、
a == b || b == c || c == a
が成り立てばよいです。
main :: IO ()
main = do
[a, b, c] <- getInts
printYn $ a == b || b == c || c == a
B問題
- 問題
- 回答
同じイベントが 2 回以上起きることはありません。と書いてあるのがポイントで、一人の人が同じ問題を複数解くことはありません。なので、
『どの問題を解いたか?』
は重要でなく
『幾つ問題を解いたか?』
が重要になります。
よって、人ごとに問題を解いた回数をIntMapとして持っておいて、イベントをこなす度に解いた問題数をインクリメントし、カウント数が問題の総数と同じであれば解答者のリストに追加していけば良いです。
main :: IO ()
main = do
[n, m, k] <- getInts
abs <- replicateM k getInts
let im = IM.fromList $ map (,0) [1 .. n]
(_, ans) =
foldl'
( \(im1, ans) [a, b] ->
let im2 = IM.adjust succ a im1
cnt = fromJust $ IM.lookup a im2
in bool (im2, ans) (im2, a : ans) (cnt == m)
)
(im, [])
abs
printList $ reverse ans
C問題(upsolved)
- 問題
- 回答
i番目が(0, 0)だった時、(a, b)のいずれかがiと同じであればその問題が次の解ける問題になります。これを繰り返していって解いた問題の数をカウントする問題です。
最初は時系列順に上から問題を解いていくと勘違いしていたので、Setで次の解ける問題を保持し、foldl'で回していました。
その回答が以下になります。
https://atcoder.jp/contests/abc424/submissions/69484808
main :: IO ()
main = do
n <- readLn @Int
abs <- zip [1 ..] <$> replicateM n getInts
let ans =
foldl'
( \s (i, [a, b]) ->
if a `IS.member` s || b `IS.member` s || (a == 0 && b == 0)
then IS.insert i s
else s
)
IS.empty
abs
print $ IS.size ans
この回答の場合、サンプルはパスしますが、提出時にWAとなってしまいます。
実際は時系列順に解くのではなく、(0, 0)となる問題から出発し、次の解ける問題へと繋げていくグラフのような問題となります。
たとえば、この解法だと以下のような入力だとWAになります。
3
0 0
4 3
1 2
この場合、問題を解く順番は以下のようになります
スキル習得順序: 1 → 3 → 2
┌─────────────────┐
│ ↓
① ② ③
↑────────┘
習得の流れ:
①スキル1 (初期習得済み)
↓
③スキル3 (スキル1があるので習得可能)
↓
②スキル2 (スキル3があるので習得可能)
このような入力でもPassするためには、bfsもしくはdfsで解く必要があります。さらに、始点となる(0, 0)は複数あるので、実際解く時は複数始点となります。
コンテスト中にここまで気づくことができたのですが、時間内に複数始点bfs, dfsを書けずに終わってしまいました。
それぞれの回答を載せておきます。(ちなみに、私の持っているimmutable版だとTLEになりました。)
解答(bfs版)
main :: IO ()
main = do
n <- readLn @Int
abs <- zip [1 ..] <$> replicateM n getInts
let init = [i | (i, [a, b]) <- abs, a == 0, b == 0]
g = buildG (1, n) $ concat [[[a, i], [b, i]] | (i, [a, b]) <- abs, a /= 0, b /= 0]
ans = bfsRunSTUArray n (g !) init
print $ length $ findArrayIndices id ans
bfsRunSTUArray :: Int -> (Int -> [Int]) -> [Int] -> UArray Int Bool
bfsRunSTUArray n getNext initNodes = runSTUArray $ do
visited <- newArray (1, n) False
queueRef <- newSTRef initNodes
let loop = do
queue <- readSTRef queueRef
case queue of
[] -> return visited
currentLevel -> do
writeSTRef queueRef []
nextLevel <- foldM processNode [] currentLevel
if null nextLevel
then return visited
else do
writeSTRef queueRef nextLevel
loop
processNode acc curr = do
isVisited <- readArray visited curr
if isVisited
then return acc
else do
writeArray visited curr True
let neighbors = getNext curr
return (neighbors ++ acc)
loop
解答(dfs版)
main :: IO ()
main = do
n <- readLn @Int
abs <- zip [1 ..] <$> replicateM n getInts
let init = [i | (i, [a, b]) <- abs, a == 0, b == 0]
g = buildG (1, n) $ concat [[[a, i], [b, i]] | (i, [a, b]) <- abs, a /= 0, b /= 0]
ans = dfsRunSTUArray n (g !) init
print $ length $ findArrayIndices id ans
dfsRunSTUArray :: Int -> (Int -> [Int]) -> [Int] -> UArray Int Bool
dfsRunSTUArray n getNext initNodes = runSTUArray $ do
visited <- newArray (1, n) False
stackRef <- newSTRef initNodes
let loop = do
stack <- readSTRef stackRef
case stack of
[] -> return visited
(curr : rest) -> do
writeSTRef stackRef rest
isVisited <- readArray visited curr
if isVisited
then loop
else do
writeArray visited curr True
let neighbors = getNext curr
modifySTRef' stackRef (neighbors ++)
loop
loop
全体を振り返って
解法に気づくことはできたのですが、時間内に解くことができませんでした。
手持ちのbfs, dfs強化したので、次はもっと楽に解けるようになると思います。
とはいえ単純に慣れが足りないので、まずはdfs, bfsの問題を多めに解くことから始めていきます。